[Paper Review] Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting

Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting

Informer 논문에서는 Transformer를 기반으로 long sequence의 시계열 예측을 수행하는 새로운 모델을 제안합니다. 특히나 본 논문에서 다루는 Transformer의 Long sequence input/target에 따른 모델의 효율성, 효과성 문제는 NLP에서도 본래 자주 거론되던 문제였는데, Informer 모델은 시계열 데이터에 대하여 연산 complexity를 낮추면서도 효과적이고 빠르게 예측을 수행할 수 있도록 하는 방법론을 적용한 모델입니다.

💡 본 review는 논문이 설명하고 있는 순서를 그대로 따라가고 있습니다. 또한, 논문 내의 원 문장을 웬만하면 그대로 해석하여 전달하고자 하였습니다. 하지만 단순히 직역 또는 요약을 하는 것이 아니라 추가적으로 필요한 개념에 대해서는 논문에 언급되지 않았더라도 자세히 설명하고 있으니 함께 참고해주시면 감사하겠습니다. 틀린 부분이나 추가 의견이 있다면 언제든 댓글 부탁드립니다. 😀

Abstract

• Long sequence time-series forecasting (LSTF) 은 output 과 input의 정확한 long-range dependency를 효율적으로 포착할 수 있는 높은 예측 capacity를 가진 모델을 요구합니다.

• 딥러닝 분야에서 강한 파워를 보여주고 있는 Transformer는 여러 최신 연구에서 prediction capacity 증가에 대한 잠재성을 보여주고 있습니다.

• 하지만, LSTF task와 관련하여 Transformer 모델은 다음과 같은 issue들이 존재합니다.

  • Quadratic time complexity
  • High memory usage
  • Inherent limitation of the encoder-decoder architecture

• 위와 같은 문제들을 해결하기 위해서, Informer는 다음과 같이 transformer 모델을 기반으로 보다 더 효율적인 모델을 위한 방법론을 제안합니다.

  • ProbSparse self-attention mechanism
  • The self-attention distilling highlights dominating attention
  • The generative style decoder, while conceptually simple, predicts the long time-series sequences at one forward operation

Introduction

• 여러 도메인 (e.g. network monitoring, energy and smart grid management, economics, fincnace, disease propagation analysis, etc.)에 걸쳐 시계열 예측 방법이 사용되고 있는데, 우리는 과거로부터 축적된 상당한 양의 시계열 데이터를 장기적으로 예측하기 위해 활용할 수 있을 것입니다.
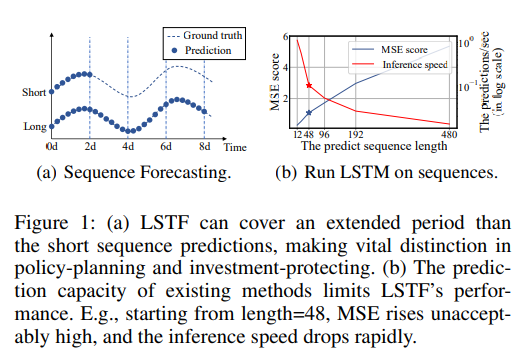
• 하지만, 현존하는 방법론들은 대부분 short-term 문제를 풀기 위해 고안된 것이 많습니다. 참고로 본 논문에 의하면, 보통 short-term 예측이라고 하면 약 48개 이하의 시점에 대한 예측을 말합니다.

• 위 그림에서 (a) 는 short sequence time series forecasting과 long sequence time series forecasting에 대한 개념적인 차이를 그래프를 통해 보여주고 있습니다. (b) 는 예측해야 할 sequence 길이에 따른 MSE score와 Inference speed를 비교하고 있는데, 그래프와 설명을 함께 살펴보면 예측 길이가 48을 넘어가는 순간부터 MSE score 값이 급진적으로 증가하고 있음을 알 수 있습니다. 또한 이 그래프에서는 초당 예측 길이(predictions/sec, log scale)로 Inference speed를 나타내고 있는데, 그 값이 가파르게 낮아지고 있는 것을 보아 sequence의 길이가 늘어날수록 추론 속도가 매우 느려지고 있음을 확인할 수 있습니다.

• LSTF를 위한 주요 과제는 long sequence에 대한 수요를 충족하기 위해 prediction capacity를 향상시키는 것입니다. 하지만 이는 다음과 같은 것들을 필요로 합니다.

  (a) long range alignment 능력
  (b) 긴 시퀀스 입력 및 출력에 대한 효율적인 연산

• 최근 딥러닝 모델을 대표한다고 볼 수 있는 가장 영향력 있는 모델은 바로 Transformer 입니다.

  • Transformer 구조는 (a) 조건에 대해서는 어느정도 타 네트워크 대비 우수하다고 볼 수 있습니다. Transformer 모델은 Recurrent나 Convolution 구조를 사용하지 않고 Attention mechanism 만을 사용하는 구조를 지니며, RNN 모델 대비 long-range dependency를 잘 포착하며 뛰어난 성능을 보이고 있습니다.
  • Transformer의 self-attention mechanism은 recurrent한 구조를 사용하지 않기 때문에 maximum path length가 $O(1)$ 이 됩니다. 여기서 maximum path length란, 특정 시점 $i$ 에서 과거 시점 $j$ 의 token과 비교하고 싶을 때 필요한 계산 횟수를 의미합니다. RNN의 경우에는 token $i$ 와 $j$ 간의 정보를 계산하려면 $|i-j|$ 만큼의 재귀적인 연산이 필요하지만, Transformer는 각 위치의 token이 독립적으로, 하나의 matrix에 의해 attention이 연산이 되기 때문에 한 쌍의 token $i$ 와 $j$에 대한 필요 연산은 1번이 됩니다.

    다음은 layer 종류 별 long-range dependency와 maximum path length에 대한 개념 이해를 돕기 위한 자료이며, 제가 발표를 진행한 영상 링크를 첨부합니다.
    ▶ 참고링크 : [Transformer Survey] #1 Transformer Basic

• 하지만, self-attention mechanism은 (b) 조건을 만족하지 못합니다. 그 이유는 $L-length$를 가진 input/output에 대해서 $L \ quadratic \ (L^2)$ 한 연산(computation)과 메모리 사용(memory consumption) 이 불가피하기 때문입니다.

  • 자연어처리 분야에서 뚜렷하게 성능을 더욱 높이기 위해 더 큰 데이터, 더 큰 모델 혹은 더 많은 양의 하드웨어 자원을 투자하는 large-scale Transformer 모델도 많이 연구되고 있습니다. 이들이 실험한 환경 세팅을 보면, 대부분 학습 과정에서 상당히 많은 개수의 GPU를 사용하고 있고 이와 같은 고가의 배치 비용은 사실상 현실적으로 LSTF 문제에 대해서는 감당할 수 없는 모델이라고 볼 수 있습니다.
  • 사실상 Transformer가 등장한 배경을 생각하면, self-attention mechanism이 long-range dependency 문제를 (RNN 대비) 효율적으로 풀고자 한 것이 맞습니다. 그러나 본 논문에서 저자가 지적하고 있는 기존의 transformer의 문제점은 이러한 transformer 구조의 효율성은 어디까지나 적당히 짧은 길이의 sequence에 대해서만 유의미하다는 것입니다. 즉, self-attention mechanism은 LSTF 문제에 적용하고자 했을 때, 주요 bottleneck으로서 작용하게 됩니다.

• 저자는 다음과 같은 질문을 던집니다. 그것은 바로 "기존의 Transformer 모델을 연산, 메모리, 구조적 측면에서 효율적이게 향상시키면서도 높은 예측 성능은 유지하고자 할 수는 없을까?" 입니다.

  👉 "Can we improve Transformer models to be computation, memory, and architecture efficient, as well as maintaining higher prediction capacity? "

• 그리고 저자는 다음과 같이 LSTF 문제와 관련하여 Vanilla Transformer (Vaswani et al. 2017) 에 대한 한계점을 정의하고 본 논문의 main contribution으로서 그에 대한 해결 방안을 제시합니다.

  [Limitation]

  1. The quadratic computation of self-attention. The atom operation of self-attention mechanism, namely canonical dot-product, causes the time complexity and memory usage per layer to be $O(L^2)$.
  2. The memory bottleneck in stacking layers for long inputs. The stack of J encoder/decoder layers makes total memory usage to be $O(J · L^2)$, which limits the model scalability in receiving long sequence inputs.
  3. The speed plunge in predicting long outputs. Dynamic decoding of vanilla Transformer makes the step-by-step inference as slow as RNN-based model (Fig.(1b)).
     

  📑 Prior Works

  🔎 위의 한계점에서 다루는 self-attention의 효율성(Efficiency) 문제를 해결하기 위한 선행 연구들은 다음과 같습니다.
  
  1) Heuristic한 방법론을 바탕으로 self-attention mechanism의 복잡도를 $O(LlogL)$로 줄인 모델 (e.g. Sparse Transformer (Child et al. 2019), LogSparse Transformer (Li et al. 2019), and Longformer (Beltagy, Peters, and Cohan 2020))
  ✔ Limitation 1만을 다루고 있음
  
  2) LSH(Locally sensitive hashing) self-attention을 제안하여 복잡도를 $O(LlogL)$로 줄인 Reformer (Kitaev, Kaiser, and Levskaya 2019)
  ✔ 하지만, Reformer는 극단적으로 긴 sequence에만 특화되어 있음 ("but it only works on extremely long sequences".)
  
  3) Linformer (Wang et al. 2020) 은 선형적 복잡도 $O(L)$을 가지는 attention기법을 제안함
  ✔ 여기서 쓰이는 projection matrix($\approx$ kernel function)는 현실 세계에 존재하는 long sequence input에 대해서 확장성을 갖도록 고정될 수 없음 (cf. linearized attention)
  
  4) (위의 선행연구와는 달리, 복잡도 측면의 접근 보다는) Long-range dependency를 잘 파악하기 위해 보조적인 hidden states를 사용한 Transformer-XL (Dai et al. 2019)과 Compressive Transformer (Rae et al. 2019).
  ✔ Limitation 1을 악화시킬 수 있고 efficiency 병목 현상을 해결하는 데 오히려 역효과가 있음

[Solution]

앞서 언급한 모든 선행 연구들은 주로 limitation 1에 대해서만 해결책을 제시하고 있고, LSTF 문제의 관점에서 limitation 2와 3을 해결하고 있진 않습니다. Prediction capcity를 향상시키기 위해서 Informer 논문은 위의 모든 limitation을 해결하고자 하였고 efficiency를 넘어선 모델 향상을 달성하였습니다. 아래 제시된 원문에 대한 자세한 내용은 Methodology 파트에서 다루도록 하겠습니다.
1. We propose Informer to successfully enhance the prediction capacity in the LSTF problem, which validates the Transformer-like model’s potential value to capture individual long-range dependency between long sequence time-series outputs and inputs.

2. We propose ProbSparse self-attention mechanism to efficiently replace the canonical self-attention. It achieves the $O(Llog L)$ time complexity and $O(Llog L)$ memory usage on dependency alignments.
3. We propose self-attention distilling operation to privilege dominating attention scores in J-stacking layers and sharply reduce the total space complexity to be $O((2−\epsilon)LlogL)$, which helps receiving long sequence input.
4. We propose generative style decoder to acquire long sequence output with only one forward step needed, simultaneously avoiding cumulative error spreading during the inference phase

Preliminary

• LSTF Problem의 정의
  • Input : $\mathcal{X}^{t}=\left\{\mathbf{x}_{1}^{t}, \ldots, \mathbf{x}_{L_{x}}^{t} \mid \mathbf{x}_{i}^{t} \in \mathbb{R}^{d_{x}}\right\}$
  • Output : $\mathcal{Y}^t=\left\{\mathbf{y}_{1}^{t}, \ldots, \mathbf{y}_{L_{y}}^{t} \mid \mathbf{y}_{i}^{t} \in \mathbb{R}^{d_{y}}\right\}$
  • LSTF 문제는 위 Output length의 길이 $L_y$가 선행 연구들 보다 길 때로 정의한다. 또한, feature dimension 의 크기가 단변량에 제한되지 않는다. $(d_y \ge1)$.
• Encoder-decoder Architecture
  • 대부분의 encoder-decoder 모델은 input representation인 $\mathcal{X}^{t}$를 encoder의 입력으로 받아 hidden state representation인 $\mathcal{H}^t$로 인코딩한 후, 이 $\mathcal{Y}^{t}$ from $\mathcal{H}^{t}=\left\{\mathbf{h}_{1}^{t}, \ldots, \mathbf{h}_{L_{h}}^{t}\right\}$를 받아 output representation인 $\mathcal{Y}^t$를 출력한다.
  • 학습 완료 후, 추론(Inference) 과정은 step-by-step 과정을 포함하는데, 이는 본 논문에서 "dynamic decoding"이라고 칭하고 있습니다. 본 논문에서 dynamic이라는 용어를 쓴 이유는, decoder가 매 step마다 이전 $k$-th hidden state인 $\mathbf{h}_{k}^{t}$와 output인 $\mathbf{y}_{k}^{t}$를 받아서 $\mathbf{h}_{k+1}^{t}$를 생성하고 $(k+1)$-th $\mathbf{y}_{k}^{t+1}$에 해당하는 값을 예측하기 때문입니다.
• Input Representation
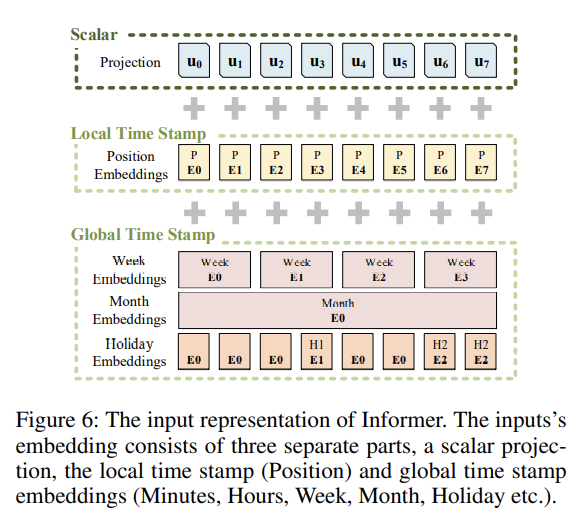
  • 본 논문에서는 uniform input representation을 사용하는데, 이는 아래의 그림과 같이 시계열 데이터의 global positional context 정보와 local temporal context 정보를 잘 반영할 수 있도록 합니다. Scalar는 input $x_i^t$을 $d_{model}$ 차원으로 projection 시킨 값이며, Local Time Stamp은 일반적인 transformer의 Positional Encoding 방식으로 fixed 값을 사용하고, Global Time Stamp는 학습 가능한(learnable) embedding을 사용합니다.

Methodology

• 현재 존재하는 시계열 예측 방법론은 크게 두 가지로 나눠볼 수 있습니다.
  [1] Classical time-series models : 확률 통계적 방법론(e.g. Bayesian Inference), 고전 머신러닝 방법론(e.g. ARIMA)
  [2] Deep Learning techniques : RNN을 활용한 encoder-decoder 기반의 모형과 그 변형 모델들
• Informer는 encoder-decoder 구조를 가지고 있으며 LSTF 문제를 푸는 것을 목적으로 하고 있습니다. Informer 모델의 큰 구조는 다음과 같습니다. 각 부분에 대한 상세한 설명은 아래에 이어서 다루도록 하겠습니다.

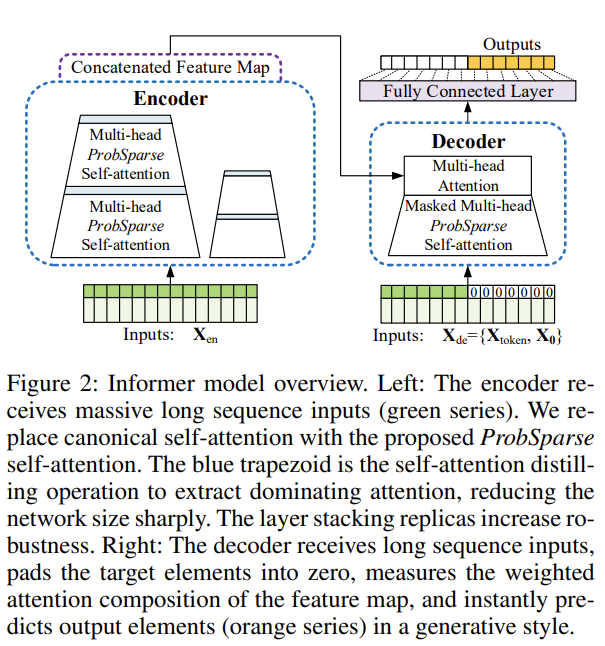
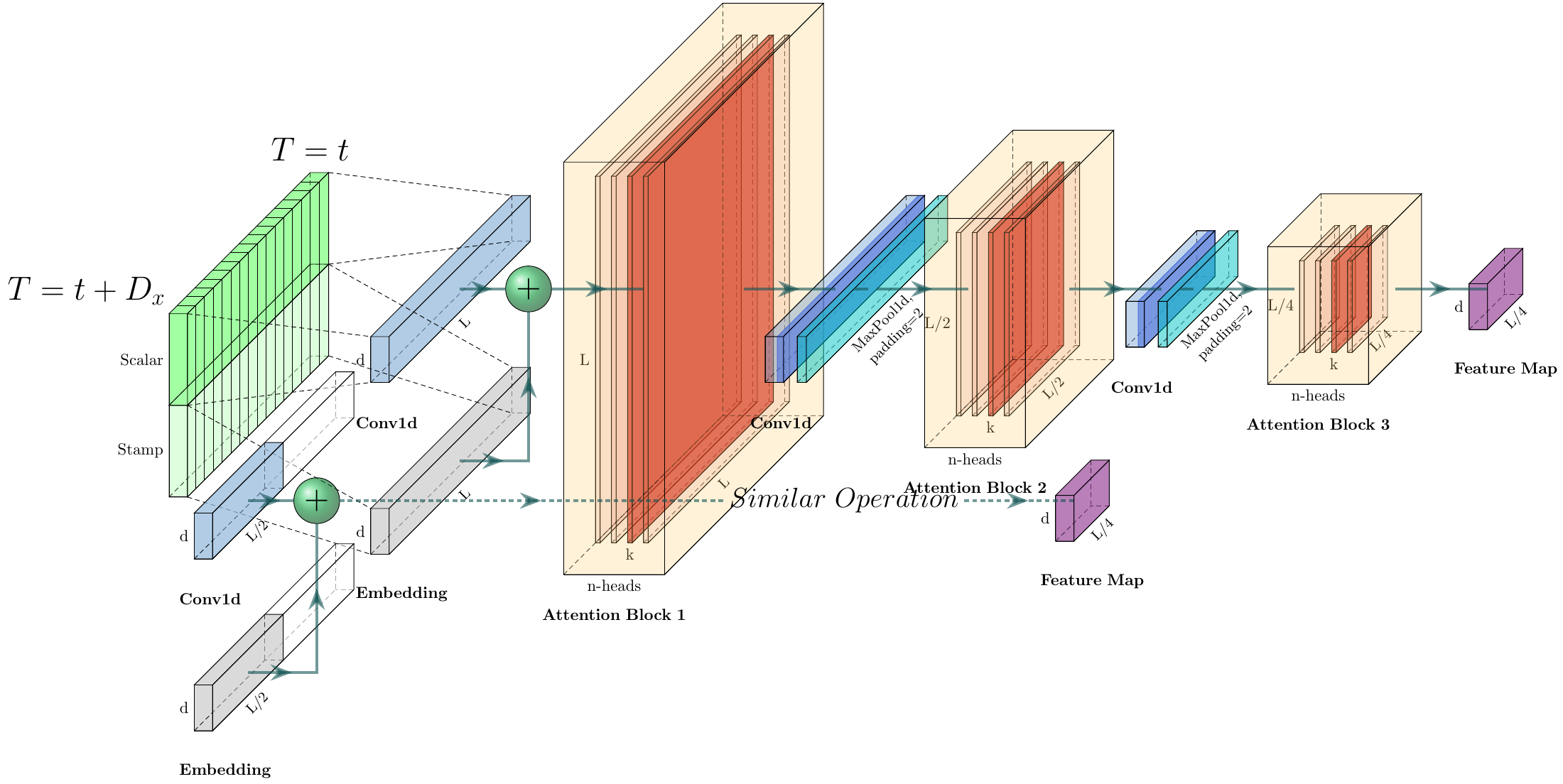
• 왼쪽 : Encoder가 긴 sequence를 input으로 받고 있는 그림이며, Informer에서는 $ProbSparse$ self-attention을 사용합니다. 여기서 파란색 사다리꼴 부분은 지배적인 attention을 추출하고 network size를 줄이기 위한 self-attention distilling operation을 의미합니다. 옆에 작은 사이즈의 복제된 encoder는 이는 모델의 robustness의 증가시키는 역할을 합니다.
• 오른쪽 : Decoder가 긴 sequence를 input으로 받고 있는 그림이며, 예측해야하는 target 부분은 0으로 padding이 되어 있습니다. 디코더는 이 input을 받아 Encoder로부터 생성된 concatenated feature map과 encoder-decoder attention을 수행하게 되어 한번에 output(주황색 부분)을 예측하게 됩니다.

🌟 자 그럼, 이제부터 본격적으로 Informer에서 다루는 방법론의 핵심 내용을 크게 세 부분으로 나누어 하나씩 살펴보도록 하겠습니다.

Part 1. Efficient Self-attention Mechanism

우선, 본 논문에서 언급하는 canonical self-attention이란, 기존의 transformer 모델이 사용하고 있는 전형적인 self-attention 방법을 의미합니다.

Vanilla Transformer 모델의 Attention에 대한 기본 개념을 알고 있다고 가정하고 아래에 설명을 이어가도록 하겠습니다. 혹시, Attention에 대한 기본 개념 보충이 필요하시다면 제가 간략하게 발표를 진행했던 영상의 일부(link)를 참고해주시면 좋을 것 같습니다.

기존 transformer에서는 Scaled dot-product attention을 다음과 같이 구합니다.

$\mathcal{A}(\mathbf{Q}, \mathbf{K}, \mathbf{V})=$ $\operatorname{Softmax}\left(\mathbf{Q K}^{\top} / \sqrt{d}\right) \mathbf{V},$
where $\mathbf{Q} \in \mathbb{R}^{L_{Q} \times d}, \mathbf{K} \in \mathbb{R}^{L_{K} \times d}$ $\mathbf{V} \in \mathbb{R}^{L_{V} \times d}$ and $d$ is the input dimension.

만약, 위 수식을 $\mathrm{Q}, \mathbf{K}, \mathbf{V}$의 $i$ 번째 행 벡터를 의미하는 $\mathbf{q}_{i}, \mathbf{k}_{i}, \mathbf{v}_{i}$ 로 자세히 쪼개어 본다면, $i$ 번째 query에 대한 attention은 kernel smoother를 활용하여 다음과 같이 수식이 정의될 수 있습니다. (💡 kernel smoother는 query와 key의 내적을 근사하는 하나의 함수라고 생각하시면 됩니다.)

$Equation$ $(1)$

$\mathcal{A}\left(\mathbf{q}_{i}, \mathbf{K}, \mathbf{V}\right)=\sum_{j} \frac{k\left(\mathbf{q}_{i}, \mathbf{k}_{j}\right)}{\sum_{l} k\left(\mathbf{q}_{i}, \mathbf{k}_{l}\right)} \mathbf{v}_{j}=\mathbb{E}_{p\left(\mathbf{k}_{j} \mid \mathbf{q}_{i}\right)}\left[\mathbf{v}_{j}\right],$

where $p\left(\mathbf{k}_{j} \mid \mathbf{q}_{i}\right)=k\left(\mathbf{q}_{i}, \mathbf{k}_{j}\right) / \sum_{l} k\left(\mathbf{q}_{i}, \mathbf{k}_{l}\right)$

위의 식에서 사용한 kernel smoother $k\left(\mathbf{q}_{i}, \mathbf{k}_{j}\right)$는 asymmetric exponential kernel로 $\exp \left(\mathbf{q}_{i} \mathbf{k}_{j}^{\top} / \sqrt{d}\right)$를 사용합니다. Self-attention은 value값과 $p\left(\mathbf{k}_{j} \mid \mathbf{q}_{i}\right)$ 확률을 결합하여 output을 얻게 됩니다. 이 과정은 quadratic한 횟수의 dot-product 연산과 $\mathcal{O}\left(L_{Q} L_{K}\right)$ 만큼의 메모리 사용을 필요로 합니다. 그리고 이는 prediction capacity를 향상시키는 데에 주요 한계점으로 작용하게 됩니다.

몇몇 선행 연구들은 self-attention의 확률분포가 sparsity함을 보이고자 하였습니다. 우선, 어떤 matrix가 sparse하다는 것은 행렬의 대부분의 값이 0인 것을 말합니다. 따라서 Sparse한 attention matrix라고 하면, attention score값이 대부분 낮은 상관관계를 의미하는 0에 가까운 값들로 이루어진 것을 의미합니다. 이러한 개념을 바탕으로 선행 연구들은 $p\left(\mathbf{k}_{j} \mid \mathbf{q}_{i}\right)$ 들 중에서 performance에 유의미한 영향을 끼치지 않는 것을 제외하는 "selective" counting strategies를 고안하곤 하였습니다.

[EX] Sparse Transformer (Child et al. 2019), LogSparse Transformer (Li et al. 2019), Longformer (Beltagy, Peters, and Cohan 2020)

Sparse Attention에 대해서는 다음 영상에서 자세히 다루고 있으니 참고하시면 좋을 것 같습니다.
▶ 참고링크 : [Transformer Survey] #2 Sparse Attention

하지만, 본 논문에서는 앞서 제안된 다양한 선행연구의 Sparse Attention은 heuristic 방법론을 따르고 있으며 각 multi-head self attention을 동일한 전략으로 다루고 있다는 점에서 이론적 분석에 한계가 있다고 지적합니다.

이 논문에서 말하는 heuristic한 방법론은, query나 key를 선택할 때 잠재된 어떠한 실질적 의미/역할을 고려하는 것이 아니라 단순히 random하게 혹은, 일정 window 구간으로 한정하는 방식 등을 사용한 것을 의미합니다.

따라서 본 논문에서는 Sparse Attention을 생성하는 새로운 접근 방식을 제안합니다. 그리고 아래의 그림처럼 "sparsity"한 self-attention은 꼬리가 긴 분포(long tail distribution)을 가집니다. 이는 소수의 dot-product pairs만이 주요 어텐션에 기여하고 다른 dot-product pairs는 trivial attention, 즉 영향력이 낮은 attention을 생성한다는 것을 의미합니다.

이러한 배경으로 본 논문에서는 다음과 같은 질문을 던집니다.

🕵️‍ 어떻게 유의미한 dot-product pair를 구분해낼 것인가?

Part 1-1 Query Sparsity Measurement

$Equation$ $(1)$의 식을 보면, $i$ 번째 query의 모든 key에 대한 attention은 $p\left(\mathbf{k}_{j} \mid \mathbf{q}_{i}\right)$ 로 정의가 되고, 그 output은 value $\mathbf{v}$와 결합됩니다. 여기서 본 논문이 제안하는 핵심 아이디어는 dominant dot-product pairs , 즉 유의미한 query($i$)-key(모든 $j$) pairs의 분포는 uniform 분포로부터 상이 하다는 것입니다. 만약, $p\left(\mathbf{k}_{j} \mid \mathbf{q}_{i}\right)$ 의 분포가 uniform 분포인 $q\left(\mathbf{k}_{j} \mid \mathbf{q}_{i}\right)=1 / L_{K}$에 근사한다면, self-attention이 value $\mathbf{V}$와 가중합할 때 trivial한 영향을 주게 되고 상대적으로 불필요한 query로 작용하게 됩니다. 따라서 $p$와 $q$ 분포의 유사도는 중요한 query를 구분해 내는 지표로 사용될 수 있습니다. 본 논문에서는 Kullback-Leibler divergence를 통해 이 유사도를 측정하였습니다.

• Kullback-Leibler divergence

위 KL-divergence 수식에서 맨 마지막의 상수항 term ($\ln L_k$)를 제거하고 $i$ 번째 query에 대한 sparsity 측정 방법을 다음과 같이 정의합니다.

• Simpler Kullback-Leibler divergence $Equation$ $(2)$

  $M\left(\mathbf{q}_{i}, \mathbf{K}\right)=\ln \sum_{j=1}^{L_{K}} e^{\frac{\mathrm{q}_{i} \mathbf{k}_{j}^{\top}}{\sqrt{d}}}-\frac{1}{L_{K}} \sum_{j=1}^{L_{K}} \frac{\mathbf{q}_{i} \mathbf{k}_{j}^{\top}}{\sqrt{d}}$

  위 식에서 첫번째 term은 $\mathbf{q}_{i}$의 모든 key에 대한 Log-Sum-Exp (LSE) 값을 의미하고, 두번째 term은 $\mathbf{q}_{i}$의 모든 key에 대한 산술평균 값을 의미합니다. 만약, $i$ 번째 query가 큰 $M\left(\mathbf{q}_{i}, \mathbf{K}\right)$ 값을 가지게 된다면, 그 attention probability $p$는 보다 "diverse", 다양한 확률 값을 가지게 될 것이고 유의미한 dot-product pairs를 가질 가능성이 더 높다고 볼 수 있습니다. 즉, sparsity한 attention이 가지는 long tail distribution에서 header 부분에 해당하는 pair가 됩니다.

Part 1-2 $ProbSparse$ Self-attention

본 논문은 $Equation$ $(2)$에서 제안된 측정 방법론을 바탕으로 각 key들이 지배적인 $u$ 개의 query에만 집중을 할 수 있도록 하는 $ProbSparse$ self-attention을 새롭게 정의합니다.

• $ProbSparse$ Self-attention $Equation$ $(3)$
  $\mathcal{A}(\mathbf{Q}, \mathbf{K}, \mathbf{V})=\operatorname{Softmax}\left(\frac{\overline{\mathbf{Q}} \mathbf{K}^{\top}}{\sqrt{d}}\right) \mathbf{V}$

여기서 $\overline{\mathbf{Q}}$ 는 같은 크기의 $\mathbf{q}$로 구성된 sparse matrix를 의미하며, 이 sparse matrix는 측정 지표인 $M\left(\mathbf{q}, \mathbf{K}\right)$ 값을 기준으로 하여 오직 Top-$u$개의 query 만으로 구성됩니다. 본 논문에서 $u$는 hyper parameter로 정의되는 sampling factor인 $c$ 와 $\ln L_{Q}$의 곱으로 계산된 $u=c \cdot \ln L_{Q}$ 값을 사용하고 있습니다 (cf. $c=5$). 이 방식을 통해 $ProbSparse$ self-attention은 각 query-key lookup에 대해 오직 $\mathcal{O}(\ln L_Q)$ 만큼의 query에 대해서만 dot-product 연산을 수행하게 되며, $\mathcal{O}(L_K\ln L_Q)$ 만큼의 layer memory를 사용하게 됩니다. Multi-head 관점에서 보면, 각 head 별로 각기 다른 sparse query-key 쌍을 생성하게 되기 때문에 sampling으로 인한 심각한 정보 손실을 방지할 수 있게 됩니다.

하지만, 결국 우리는 top-$u$개의 유의미한 query를 잘 추출하기 위해 $M\left(\mathbf{q}, \mathbf{K}\right)$ 값을 모두 하나씩 계산해보아야 합니다. 결국 $\mathcal{O}(L_Q L_K)$ 만큼의 quadratic한 연산이 필수적이게 되는 것입니다. 따라서, 본 논문에서는 효율적으로 query sparsity 정도인 $M\left(\mathbf{q}, \mathbf{K}\right)$ 를 측정할 수 있는 empirical approximation 방법론 을 제안합니다.

우선, 논문에서는 다음과 같은 Lemma 1 (보조정리, 증명은 Appendix D.1 참조) 을 바탕으로 실제 query sparsity 측정값인 $M\left(\mathbf{q}, \mathbf{K}\right)$ 값의 범위를 제한합니다. 그리고 query와 key가 동일할 때에도 아래 정리가 성립한다는 것을 보였습니다.

Lemma 1. For each query $\mathbf{q}_{i} \in \mathbb{R}^{d}$ and $\mathbf{k}_{j} \in \mathbb{R}^{d}$ in the keys set $\mathbf{K}$, we have the bound as $\ln L_{K} \leq M\left(\mathbf{q}_{i}, \mathbf{K}\right) \leq$ $\max _{j}\left\{\mathbf{q}_{i} \mathbf{k}_{j}^{\top} / \sqrt{d}\right\}-\frac{1}{L_{K}} \sum_{j=1}^{L_{K}}\left\{\mathbf{q}_{i} \mathbf{k}_{j}^{\top} / \sqrt{d}\right\}+\ln L_{K} .$ When $\mathbf{q}_{i} \in \mathbf{K}$, it also holds.

이 보조정리에서 도출된 범위를 바탕으로 $M\left(\mathbf{q_i}, \mathbf{K}\right)$를 근사한 수식은 다음과 같습니다.

$Equation$ $(4)$

이 식은 Lemma 1에서 도출된 $M\left(\mathbf{q}, \mathbf{K}\right)$의 상한값에서 상수항 term인 $\ln L_{K}$ 부분을 제거한 것과 같습니다. 그리고 이 식은 query $i$에 대해서 비교되는 모든 key $j$ 중에서 일부를 random sampling 하여 계산이 됩니다. 논문에서 key의 sample 개수는 실제 코드 구현 확인 결과 $L_{K} \ln L_{Q}$ 를 사용하고 있습니다. 주의할 점은, 이는 top-$u$개의 query를 뽑기 위해 필요한 근사식 $\bar{M}\left(\mathbf{q}, \mathbf{K}\right)$ 값 계산에 사용될 key sample을 뽑기 위한 값입니다.

🔎 어떠한 근거로 위의 근사식을 사용할 수 있게 되는 걸까요?

이는 논문 Appendix에 첨부된 다음의 보조 정리와 명제의 증명을 근거로 하고 있습니다.

1) Appendix D.1에 첨부된 Top-$u$에 대한 범위를 제한한 Lemma 1 (보조 정리)
2) Appendix D.2에 첨부된 Proposition 1 (명제)

Proposition 1. Assuming $\mathbf{k}_{j} \sim \mathcal{N}(\mu, \Sigma)$ and we let $\mathbf{q} \mathbf{k}_{i}$ denote set $\left\{\left(\mathbf{q}_{i} \mathbf{k}_{j}^{\top}\right) / \sqrt{d} \mid j=1, \ldots, L_{K}\right\}$, then $\forall M_{m}=$ $\max _{i} M\left(\mathbf{q}_{i}, \mathbf{K}\right)$ there exist $\kappa>0$ such that: in the interval $\forall \mathbf{q}_{1}, \mathbf{q}_{2} \in\left\{\mathbf{q} \mid M(\mathbf{q}, \mathbf{K}) \in\left[M_{m}, M_{m}-\kappa\right)\right\}$, if $\bar{M}\left(\mathbf{q}_{1}, \mathbf{K}\right)>$ $\bar{M}\left(\mathbf{q}_{2}, \mathbf{K}\right)$ [cond 1] and $\operatorname{Var}\left(\mathbf{q} \mathbf{k}_{1}\right)>\operatorname{Var}\left(\mathbf{q} \mathbf{k}_{2}\right)$ [cond 2], we have high probability that $M\left(\mathbf{q}_{1}, \mathbf{K}\right)>M\left(\mathbf{q}_{2}, \mathbf{K}\right)$.
※ Typically the condition 2 can be relaxed, and we can believe that if $\mathcal{q}_1$, $\mathcal{q}_2$ fits the condition 1 in our proposition, we have $M\left(\mathbf{q}_{1}, \mathbf{K}\right)>M\left(\mathbf{q}_{2}, \mathbf{K}\right)$.

이에 대한 증명이 매우 복잡하고 어렵기 때문에 본 글에서는 증명을 다루지는 않고 큰 컨셉만 짚고 넘어가도록 하겠습니다.

우선, Lemma 1은 Top-$u$개를 뽑기 위한 sparsity measurement($M$)의 range를 한정합니다. 그리고 Proposition 1은 range 안에서 sparsity measurement를 approximation하는 수식($\bar{M}$)가 $M$을 대표할 수 있음을 뒷받침합니다.

특히, Proposition 1은 sampling된 key와의 sparsity measurement 계산을 통해 구해진 query 중요도 순서가 모든 key와의 sparsity measurement 계산을 통해 구해진 중요도 순서와 일치한다는 것을 보장해 줍니다. 다시 말해, 잘못 sampling된 key를 바탕으로 sparsity measurement를 계산하면, query 중요도 순서가 달라질 가능성이 있는데, 본 논문에서는 Proposition 1에 대한 경험적, 이론적 증명을 통해 제안된 approximation 수식($\bar{M}$)이 유효함을 보입니다.

정리하면, 근사식 $\bar{M}$은 실제 모든 key에 대해서 내적을 구해보는 방식으로 계산된 $M$이 갖는 범위(by Lemma 1)를 만족하면서 $M$을 대표(by Proposition 1)할 수 있게 됩니다.

이 식의 구성을 자세히 살펴보면 , $\bar{M}\left(\mathbf{q}_{i}, \mathbf{K}\right)$ 의 첫번째 term은 query $i$에 대하여 sampling 된 key $j$들과의 내적을 구한 것의 최댓값(max)이고 두번째 term은 query $i$에 대하여 sampling된 key $j$들과의 내적값을 구한 것의 평균(mean)을 의미합니다. 이 둘의 차를 가지고 Top-$u$의 query에 대해서만 attention을 계산하게 됩니다. 실제로 self-attention 연산에서 input query와 key의 길이는 보통 동일하기 떄문에 $L_Q=L_K=L$ 이라고 볼 수 있고, $ProbSparse$ self-attention의 총 시간 복잡도(time complexity)와 공간 복잡도(space complexity)는 $\mathcal{O}(L\ln L)$ 이 됩니다.

🔅 참고
논문에서 "Under the long tail distribution, we only need to randomly sample $U = L_K lnL_Q$ dot-product pairs to calculate the $\bar{M}(q_i, K)$"
라는 부분이 있는데 여기서 $U$는 최종 top-$u$개의 query를 바탕으로 모든 key 들과 필요한 내적 연산(query-key pair)이 총 $U$에 근사한다는 의미입니다. ($U \ne u$)

[개인적인 의문 및 해석]
저는 개인적으로 이 부분에 대해서 순간 한 가지 의문이 들었는데, 그것은 바로 query를 top-$u$개 뽑았으면, self-attention에서 query와 key 대상은 동일하니 key도 top-$u$개 query에 대응되는 것만 뽑아 attention을 계산하면 되지 않을까? 입니다. 이에 대해 고민 끝에 스스로 해답을 내린 결론은 다음과 같습니다. key sampling은 오직 query 중요도 계산을 위한 사용되는 수단, trick일 뿐이라는 것입니다. 실제 self-attention을 구할 때에는, 추출된 특정 query에 대해서 누구에게 집중적으로 attend 되었는가를 정확히 보려면 모든 key들과 비교를 해서 정보를 얻어야 한다는 것입니다. 또한, 모든 key를 이용해야 global 혹은 local하게 내재된 position 정보를 어느정도 반영할 수 있다고 볼 수 있습니다. 이 해석은 제 개인적인 의견이니 참고해주시고 혹시 다른 의견 있으시면 공유해주시면 감사하겠습니다! 🙋‍

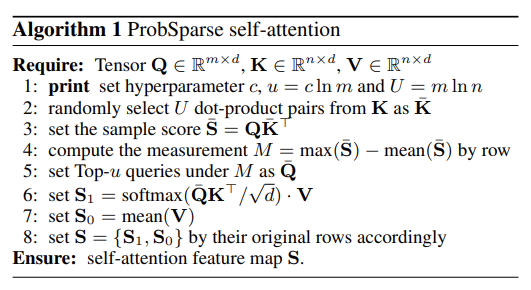
다음은 Appendix E에 첨부된 $ProbAparse$ self-attnetion의 구현 알고리즘이며, 위에서 설명한 수식이 모델에서 어떻게 동작하는 지를 확인할 수 있습니다.

Part 2. Encoder: Allowing for Processing Longer Sequential Inputs under the Memory Usage Limitation

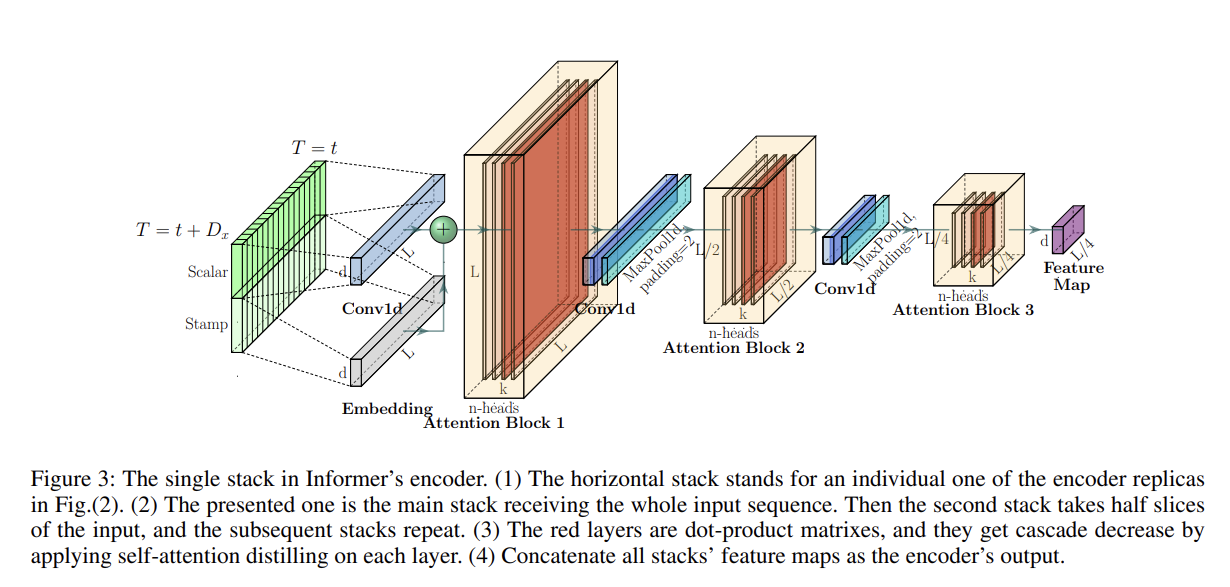
Informer의 encoder는 long sequential input들에 대하여 robust한 long-range dependency를 추출할 수 있도록 설계되었습니다. Preliminary에서 설명한 것처럼 Input representation을 구한 후, $t$ 번째 sequence에 해당하는 input $\mathcal{X}^t$는 encoder의 embedding matrix인 $\mathbf{X}_{\mathrm{en}}^{t} \in \mathbb{R}^{L_{x} \times d_{\text {model }}}$ 로 embedding이 됩니다. 특히, 위에 첨부된 Figure 3처럼 원 데이터의 scalar 값은 conv1d를 통해 projection되고, global/local 시간 정보인 stamp 값은 각각 positional embedding/encoding을 통해 embedding됩니다. 이렇게 생성된 같은 크기 ${L_{x} \times d_{\text {model }}}$ 차원의 embedding matrix는 서로 더해져 최종적으로 encoder의 embedding을 구성하게 됩니다.

Part 2-1 Self-attention Distilling

$ProbSparse$ self mechanism의 결과로 얻어진 encoder의 feature map은 일부 value $\mathbf{V}$의 불필요한 가중합을 포함하고 있습니다. 그 이유는, query 들은 top-$u$개가 사용되지만, 각 query들은 모든 key에 대해서 attention을 구하기 때문입니다. 또한, scaled-dot product attention의 정의를 생각해보면, 행렬의 내적 연산을 위해 key와 value의 길이(행의 수)가 같기 때문에 불필요한 value의 가중합을 포함한다고 말할 수 있는 것입니다. (참고 : Scaled dot-product attention 정의)

본 논문에서는 이러한 redundant 한 값을 포함한 feature map으로부터 주요한 정보만을 추출하여 다음 layer에 전달할 feature map을 구성하고자 하였고, 이를 위해서 conv1d와 maxpooling을 사용하여 self-attention distilling을 수행하였습니다.
$j$번째 layer에서 $(j+1)$번째 layer로의 distilling 과정은 다음과 같이 정의됩니다.

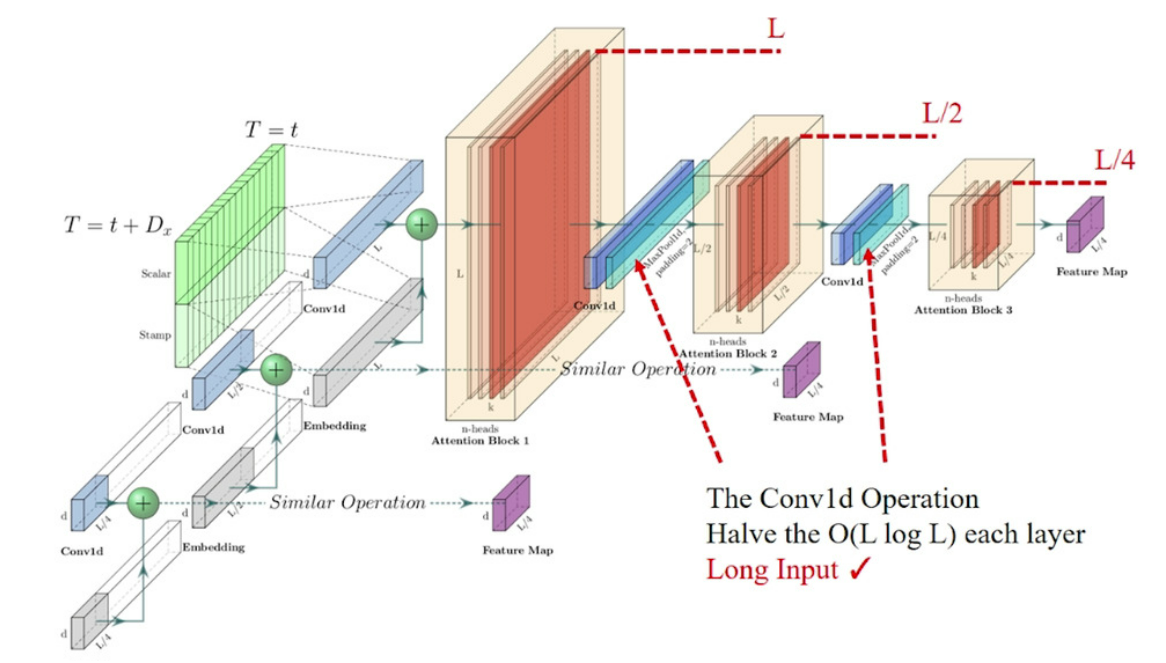
수식에서 $[\cdot] \mathrm{AB}$는 attention block을 의미하고, 논문에서는 kernel width=3인 1-D convolution을 사용하였습니다. 그리고 stride 2 의 max-pooling layer를 사용하여 이전 layer의 attention input인 길이 $L$의 $\mathbf{X}^t$ 는 attention을 거친 후, 절반의 길이 $L/2$로 압축됩니다. 이는 총 메모리 사용량을 $\mathcal{O}((2-\epsilon) L \log L)$로 감소시키는 효과를 갖습니다. 여기서 $\epsilon$ 은 아주 작은 상수값입니다. 이 식은 self-attention computation complexity에 해당하는 메모리 $L \log L$이 $2-\epsilon$ 배 만큼 필요하다는 것을 의미합니다. 예를 통해 자세히 설명하면, 첫번째 layer의 필요 메모리 사용량은 $\mathcal{O}((1) L \log L)$이고, 두번째 layer에서는 절반의 길이의 input이 사용되므로 $\mathcal{O}((1/2) L \log L)$, 세번째 layer에서는 그의 절반인 $\mathcal{O}((1/4) L \log L)$ 가 필요합니다. 이는 layer가 증가할 수록 같은 규칙이 적용되며, 등비수열의 합으로서 필요한 메모리를 계산해보면, $(1+1/2+1/4+1/8 +\dotsm)$ 만큼의 메모리 사용량 $L \log L$이 필요하다고 볼 수 있습니다. 이를 무한대의 layer, 즉 무한등비수열의 합으로 계산하면 $(1+1/2+1/4+1/8 +\dotsm) \approx (2-\epsilon)$으로 근사됨을 알 수 있습니다.

추가적으로, distilling 과정의 robustness의 향상을 위해서 원래 input의 절반의 길이만큼만 input으로 받는 복제된 encoder를 추가로 구성하였고, 이때, 각 encoder 별로 생성되는 output feature map의 dimension을 맞춰주기 위해 Fig.(2)처럼 self-attention distilling layer 수를 하나씩 점진적으로 감소시킵니다. 이렇게 여러개로 stack된 encoder를 거친 output들은 concatenate되어 최종적으로 encoder의 hidden representation을 구성하게 됩니다. 이는 아래 그림과 같고, 최근 시점을 기준으로 input sequence를 절반씩 자르게 됩니다.

Part 3. Decoder: Generating Long Sequential Outputs Through One Forward Procedure

• Recap

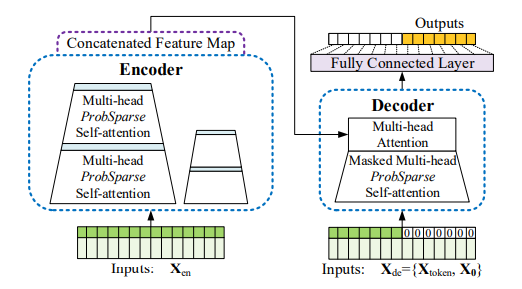
Informer 모델은 기존 Transformer의 standard decoder 구조를 취하고 있습니다. 그리고 이 decoder는 동일한 두 개의 multi-head attention layers가 stack된 형태입니다. 하지만, Informer는 generative inference라는 기법을 사용하고 있는데, 이는 long prediction, 장기 예측의 속도 급락을 완화하기 위해 사용되었습니다. Informer decoder의 input으로 들어가는 벡터는 다음과 같습니다.

본 논문에서 $\mathbf{X}_{\text {token }}^{t} \in \mathbb{R}^{L_{\text {token }} \times d_{\text {modcl }}}$는 start token이라고 불리고, $\mathbf{X}_{0}^{t} \in$ $\mathbb{R}^{L_{y} \times d_{\text {model }}}$ 는 placeholder라고 불리는데, 이 placeholder는 target sequence에 해당하는 부분이며 scalar 값($\ne$stamp)은 0으로 설정합니다. 다시 말해 placeholder 부분의 input embedding으로는 시간 정보(stamp)만 반영되는 것입니다.
Decoder에서는 Masked multi-head attention이 $ProbSparse$ self-attention 계산에 사용이 됩니다. 기존 Transformer의 Masked-self-attention처럼, 각 특정 시점에서의 예측이 미래 시점 정보에 의존하지 않도록 self-attention map을 $-\infty$ 로 masking합니다. Masked Multi-head self-attnetion 다음으로는 일반적인 Multi-head attention이 이어지며, 여기서는 기존의 transformer decoder와 동일한 방식의 encoder-decoder attention이 계산이 됩니다. 이렇게 계산되어 출력된 output은 Fully Connected Layer를 거쳐 최종 output을 생성하게 됩니다. 각 시점의 출력 dimension인 (outsize, $d_y$)는 단변량 예측($d_y=1$)인지 다변량 예측($d_y>1$)인지에 따라 달라집니다.

Part 3-1 Generative Inference

보통 NLP에서 generation task를 수행할 때, step-by-step inference와 같은 dynamic decoding을 위해 start token 이 사용되곤 합니다. 여기서 Start token이란 위에서 정의한 바와 같이 decoder에 input으로 주어지는 target의 일부 선행 정보가 되며, decoding 시에 decoder가 참조하게 되는 대상입니다. Informer는 이런 dynamic decoding 방식을 generative한 방식으로 확장하였습니다. "Decoder가 원래 generative 한 것이 아닌가?" 하는 의문이 드실 수도 있을 것 같습니다. 저도 처음 이 논문을 접했을 때 이 부분에 대한 표현이 잘 이해가 가지 않았었는데, 결론적으로 논문이 강조한 포인트는 전통적인 encoder-decoder 구조의 decoding 방식처럼 step-by-step inference를 하지 않고 한번에 generation이 가능한 decoding 방법론을 제안했다는 것입니다.

Informer의 decoder에서는 대부분의 sequence to sequence 모델에서 generation을 위해 사용하는 specific flag (e.g. [CLS] / [BOS]) 등을 사용하지 않습니다. 대신에 $L_{\text {token }}$ 길이의 sequence를 input senetence에서 뽑아 decoder input을 구성하는데, 이는 예측해야하는 것에 선행하는 일부 sequence라고 생각하시면 됩니다. 예를 들어, 기온 예측 task에서 미래의 168일 시점 정보에 대한 예측을 수행해야 한다면, 이 target sequence에 앞선 5일에 대한 정보를 "start-token" 으로 사용하게 되는 것입니다. 그리고 Informer만의 generative-style inference decoder에 $\mathbf{X}_{\mathrm{de}}=\left\{\mathbf{X}_{5 d}, \mathbf{X}_{\mathbf{0}}\right\}$ 를 넣어주게 됩니다. $\mathbf{X}_{\mathbf{0}}$ 는 input representation을 구성하는 scalar 값은 0 이지만, stamp 를 구성하는 time 정보는 포함하게 됩니다. 이 input을 바탕으로 Informer decoder는 시간이 많이 소요되는 dynamic decoding 방식을 통해서가 아니라 오직 한 단계의 forward 과정만으로 output을 예측하게 됩니다.

Part 3-2 Loss function

Informer 모델 학습에 사용되는 loss는 간단합니다. 실제 target 값과 예측된 target 값의 차이인 MSE loss function을 목적함수로 사용하여 전체 모델을 학습하게 됩니다.

Experiment

실험 부분은 결과만 간략히 보고 마무리하도록 하겠습니다. 본 논문의 실험에서는 총 5가지의 데이터셋에 대해 실험을 진행했고, 제안된 방법론을 입증하기 위한 여러 Ablation study와 hyper parameter에 대한 실험을 진행했습니다. 실험 표에서 Informer 모델을 비롯해서 주목할 만한 비교 모델은 Informer†, LogTrans, Reformer 입니다. Informer† 모델은 기존 Informer 모델에서 $ProbSparse$ self-attention을 canonical self-attention으로 대체한 모델이며 LogTrans와 Reformer 모델은 각자 나름의 방식으로 Attention computation/memory complexity를 개선한 모델입니다. 즉, 본 논문의 주요 contribution 중 하나인 Long sequence에 대한 효율적인 예측과 관련하여 실험적으로 증명해 보일 근거로서 작용하는 모델들입니다.

Univariate long sequence time-series forecasting (Table 1)

① 제안된 Informer 모델이 inference performance를 향상시켰음을 확인할 수 있습니다. 맨 아래 winning count는 각 실험 조건에서의 최고 성능을 보인 횟수를 의미하고 Informer가 총 32회로 가장 좋은 성능을 보였습니다. 또한, 모든 데이터셋에 대해서 prediction horizon(=prediction length)을 늘려갈수록 Informer의 error 증가 폭이 대체로 가장 적은 차이로 증가하고 있음을 확인할 수 있습니다.

② 또한 canonical self-attention을 사용한 Informer† 보다 $ProbSparse$ self-attention을 사용한 Informer 모델이 대체로 더 좋은 성능을 보이고 있음을 알 수 있습니다. 다른 attention 변형 모델인 LogTrans 모델과 Reformer 모델 보다도 우세한 성능을 보임을 알 수 있습니다. (참고: Reformer는 dynamic decoding 방식을 그대로 사용했고, 다른 모델들은 Informer와 같이 nonautoregressive한 decoder를 사용했다고 합니다.)

③ RNN 계열 모델인 LSTMa 대비 좋은 성능을 보였습니다. 이는 Self-attention 메커니즘과 같이 shorter network path를 가진 모델이 prediction 성능을 더 높이고 있음을 보여줍니다.

④ 평균적으로 DeepAR, ARIMA, Prophet 모델에 대해서도 Informer가 우세한 성능을 보이고 있습니다. ECL dataset에 한정해서는 336 길이 이하에 대해서는 DeepAR 모델의 성능이 제일 좋게 나타났지만, 더 긴 길이에 대해서는 Informer 모델의 성능이 더 좋았습니다. 이는 prediction capacity가 특정 task 에 따라서 살짝씩 다를 수 있음을 보여줍니다.

Multivariate long sequence time-series forecasting (Table 2)

다변량 예측은 위에서 한번 설명한 것처럼 Informer decoder의 FCN layer의 출력 dimension만 변형하여 수행할 수 있습니다.

① Informer 모델이 대부분의 방법론 대비 우수한 성능을 보이고 있음을 알 수 있고, 단변량 예측 실험 분석을 통해 알아낸 ①, ②번 특성이 다변량 예측 실험에서도 동일하게 해당됨을 알 수 있습니다.
② Informer 모델이 RNN 기반 모델인 LSTMa나 CNN 기반 모델인 LSTnet 보다 더 나은 결과를 보이고 있습니다.

추가적으로, 단변량에서는 매우 큰 폭의 성능 차이가 났었는데 다변량에서는 그정도까지로 성능을 압도하고 있진 않습니다. 이는 다변량 예측 특성상, 모델이 예측에 참고할 수 있는 정보량인 feature 수가 많다는 것을 의미하고 자연스럽게 모델의 prediciton capacity를 증가시키게 된다고 이해할 수 있습니다.

✔ 위의 Table 1, 2에서 ETTm1, ETTh1과 같이 같은 데이터 셋이 있는데, ETTm1은 15분 단위로 예측을 한 것이고, ETTh1은 1시간 단위로 예측을 수행한 것입니다. 이렇게 다른 granularity level(기본 예측 단위)로 예측을 수행하더라도 Informer 모델이 강건하게 좋은 성능을 보이고 있음을 알 수 있습니다.

The parameter sensitivity of three components in Informer (Figure 4)

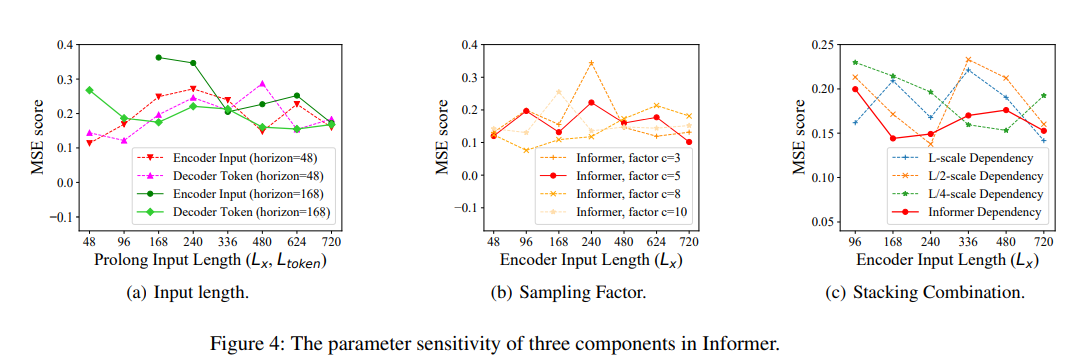
(a) 짧은 길이를 예측하는 task(e.g. horizon=48)에서는 살짝 encoder/decoder input의 길이를 늘림에 따라 초기에 살짝 MSE 값이 증가하는 양상을 보이나, 긴 길이(e.g. horizon=168)를 예측하게 될 수록 일수록 MSE 값이 점차 낮아지는 양상을 보입니다.
(b) 이는 Top-$u$개의 query를 고를 때 사용하는 $u=c \cdot \ln L_{Q}$ 수식에서 sampling factor $c$ 값에 대한 실험입니다. 논문에서는 $c=5$로 고정하여 다른 실험들을 진행했습니다..
(c) Encoder의 self-attention distilling 과정을 보완하기 위해 stack 하여 사용한 replica Encoder에 대한 실험이며, $L$ 과 $L/4$의 길이를 input으로 받는 encoder 조합(빨간선)이 가장 robust한 전략임을 확인하였습니다. 표를 보면 긴 길이일수록 long-term information을 좌우하는 input 길이에 더욱 민감함을 알 수 있습니다.

Ablation study of the $ProbSparse$ self-attention mechanism

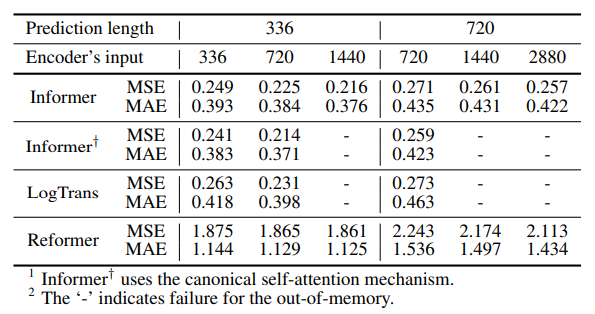
• $ProbSparse$ self-attention을 사용한 Informer가 긴 길이의 input에 대해 OOM 없이 가장 좋은 성능을 보임을 알 수 있습니다.
• 실험 설계 시에 메모리 효율성 문제를 통제하기 위하여, {batch size=8, heads=8, dim=64}로 초기 설정을 하였고, 다른 설정은 단변량 예측 task와 동일하게 설정하였습니다.

$L$-related computation statics of each layer (Table 4)

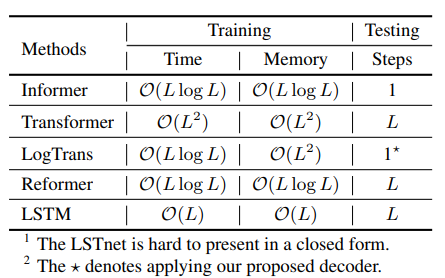
• 참고로 LogTrans 모델은 self-attention 개선을 중점으로 한 모델이며, 공정한 비교를 위해 Informer에서 제안한 decoder 모델을 사용하였습니다.

Ablation study of the self-attention distilling (Table 5)

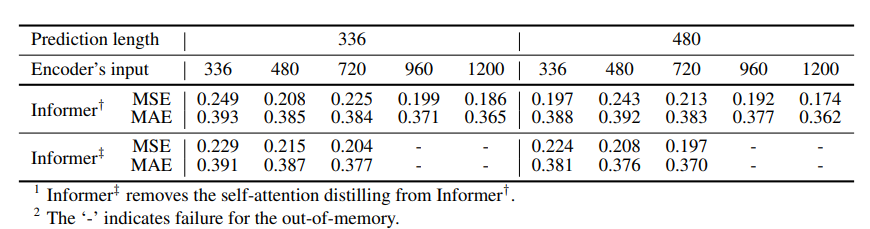
• Informer††는 self-attention distilling 과정을 Informer† 모델에서 제거한 것입니다.
• Distilling 과정이 사용되지 않는다면, long sequence input/target에 대하여 OOM이 발생하고 있습니다.

Ablation study of the generative style decoder (Table 6)

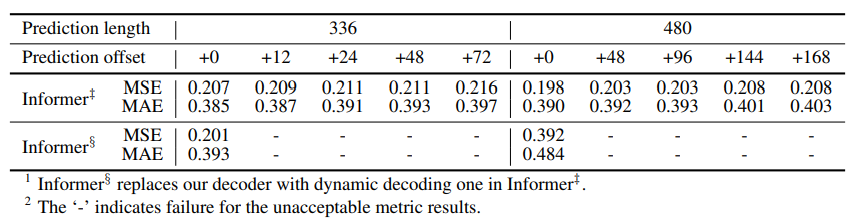
• Informer $^{\S}$는 Informer†† 모델에서 decoder를 기존 transformer decoder와 같은 dynamic decoding을 수행하는 decoder로 대체한 것입니다.
• Informer에서 제안한 generative style decoder가 예측 성능에 중요하게 작용하고 있음을 알 수 있습니다. 또한, Informer††는 prediction length 값을 조절하는 offset의 변화에 대해서도 강건한 성능을 보여주고 있습니다.
• Generative style decoder가 임의의 output에 대해서 long-range dependency를 잘 포착할 수 있으며 error accumulation도 방지할 수 있음을 알 수 있습니다.

The total runtime of training/testing phase (Figure 5)

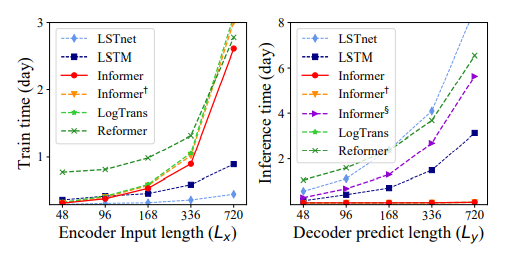
• Informer 모델이 가장 좋은 training efficiency를 보이고 있으며 testing 시에도 훨씬 빠른 decoding 속도를 보이고 있습니다.

The predicts (len=336) of Informer, Informer†, LogTrans, Reformer, DeepAR, LSTMa, ARIMA and Prophet on the ETTm dataset

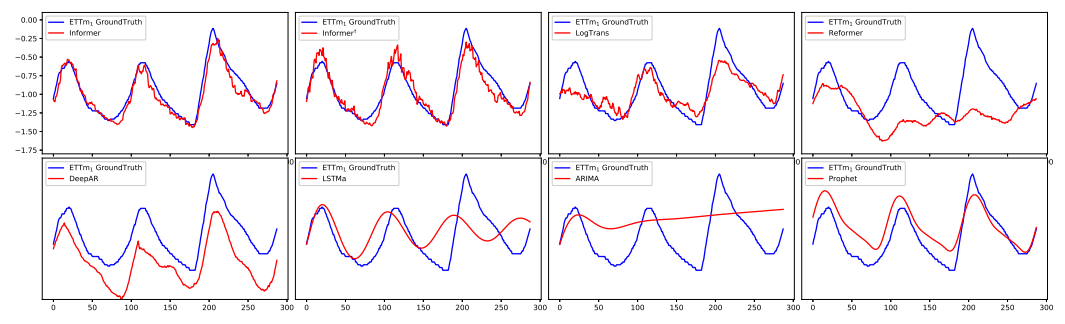
이는 Appendix에 첨부된 모델 별 Ground Truth와 예측값을 비교한 것입니다.