KNN

지능 시스템을 위한 기계학습

"기계학습"
"ML"
강의: CORNELL CS4780 "Machine Learning for Intelligent Systems"

해당 포스트는 코넬대학교 CS4780과 그 강의 자료를 정리한 내용입니다.

---

이 글을 쓰게 된 계기

기계학습에 대한 전반적인 이해와 그 알고리즘을 학습해봅시다!

---

So, what is KNN?

KNN은 친구따라 강남가는 알고리즘입니다!

자 이제 왜 제가 이런 설명을 했는지 KNN에 대해서 알아보며 이해해봅시다!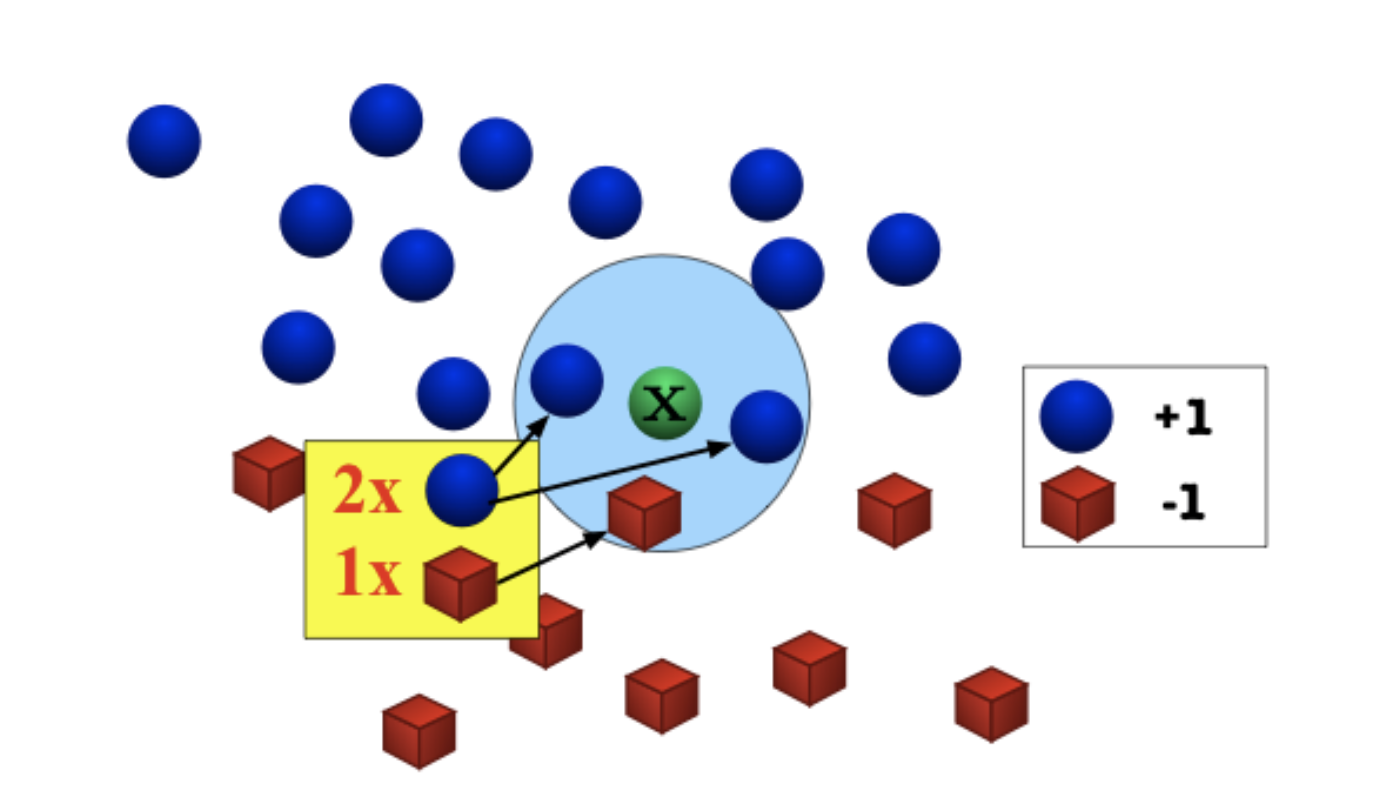

x는 저희의 test data point입니다!, 파란색과 빨간색은 train data입니다!

자 사진을 보고 이해해봅시다! 우리의 목표는 x의 label을 알아맞추는 것 입니다!

x의 친구중에 파란색이 많군요! 그렇다면 x는 파란색을 띌 가능성이 높다는 가정 하에 우리는 x의 label을 '파랑' 이라고 추측합니다.....

친구따라서 파랭이가 되어버렸네요!

그러나 이게 모든 상황에서 합리적일까요?

---

수식적 접근이 필요합니다

WTF? 자 천천히 이해해봅시다!

1. x는 test point 입니다! 우리가 label을 추청할 input 입니다!

2. Sx는 x의 가장 친한 k명의 친구 set입니다!

3. 그렇다면 Sx는 x의 친구들의 부분집합이므로 D라는 주변인 set에 포함됩니다. 그리고 Sx내의 친구는 k명 있겠죠?

4. 그럼 이 k명의 친구를 뺀 나머지 친구들은 '(프라임)으로 구분해두면

5. 모든 x'에 대하여 / Sx내의 친구들인 x''들과 x와의 거리의 최댓값은 /k명에 들지 못한 D-Sx라고 불리는 모든 덜친한 애들과의 거리보다 짧다는 것을 의미합니다.

6. 말이 뒤지게 길지만 그냥 대충 가까운 애들이 진짜 가깝다는 성질을 보여주려는 것입니다.

이것이 바로 우리가 원하는 $\mathbf{x}$의 추청 label입니다!

$mode()$는 k최근접 이웃의 최빈 label을 구하는 함수입니다!
이것이 바로 knn의 핵심입니다!

그러면 파라미터는 뭔가요?

우리는 파라미터로 쓸만한 것을 이미 알고있습니다!

$k$, 그리고 $dist$ 함수겠죠!

mode는 사실 sort혹은 search라 별 의미가 없구요.

자 이제 슬슬 구색이 맞춰지네요!

$\text{dist}(\mathbf{x}, \mathbf{z}) = \left( \sum_{r=1}^{d} |\mathbf{x}_r - \mathbf{z}_r|^p \right)^{\frac{1}{p}}.$

파라미터를 조금 일반화하기 위해 저희는 민코프스키 거리를 사용하여 일반화해봅시다!

파라미터는 $p$네요!

$p$가 1이라면 맨해튼, 2라면 유클리드....

Quiz : $p→∞$ 라면?!!!

max 함수입니다! 왜일까유? 이유는 한번 생각해보고 댓글 남겨주세유 ㅎㅎ

사실 KNN은 이게 끝입니다만... 한계가 있겠죠..?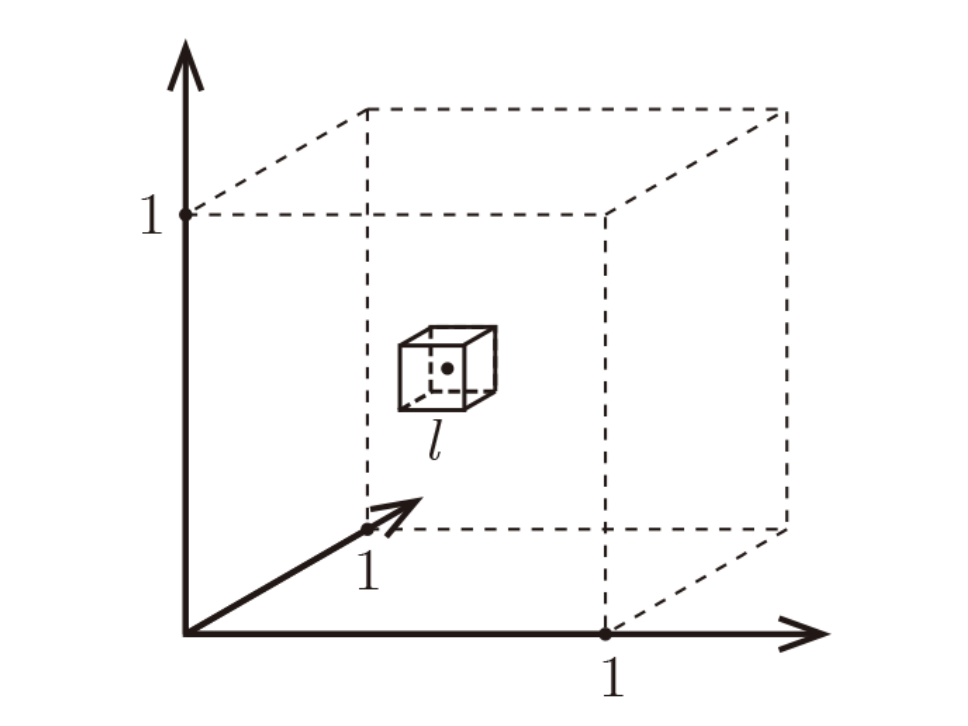

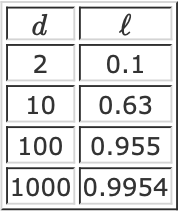
가장 유명한 Curse of Dimensionality 라는 문제점에 대하여 생각해봐야만 합니다!

$\ell^d \approx \frac{k}{n} \quad \text{and} \quad \ell \approx \left( \frac{k}{n} \right)^{\frac{1}{d}}.$

위 수식에서... $n$이 매우 클때, $d$가 커진다면 어떤 일이 일어날까요?

이때 $d$는 차원이고, $n$은 데이터의 개수입니다! 그리고 모든 data가 길이가 1인 하이퍼큐브 내에 있다고 가정하면 위 수식이 간단히 이해가 가능합니다.

$d$가 커질수록 $l$ 값이 급격하게(지수적으로) 커지네요

이때 $l$값이 1에 가까워질수록 '구분'이라는 의미가 점차 감소하겠네요, 이것이 바로

Curse of Dimensionality 입니다..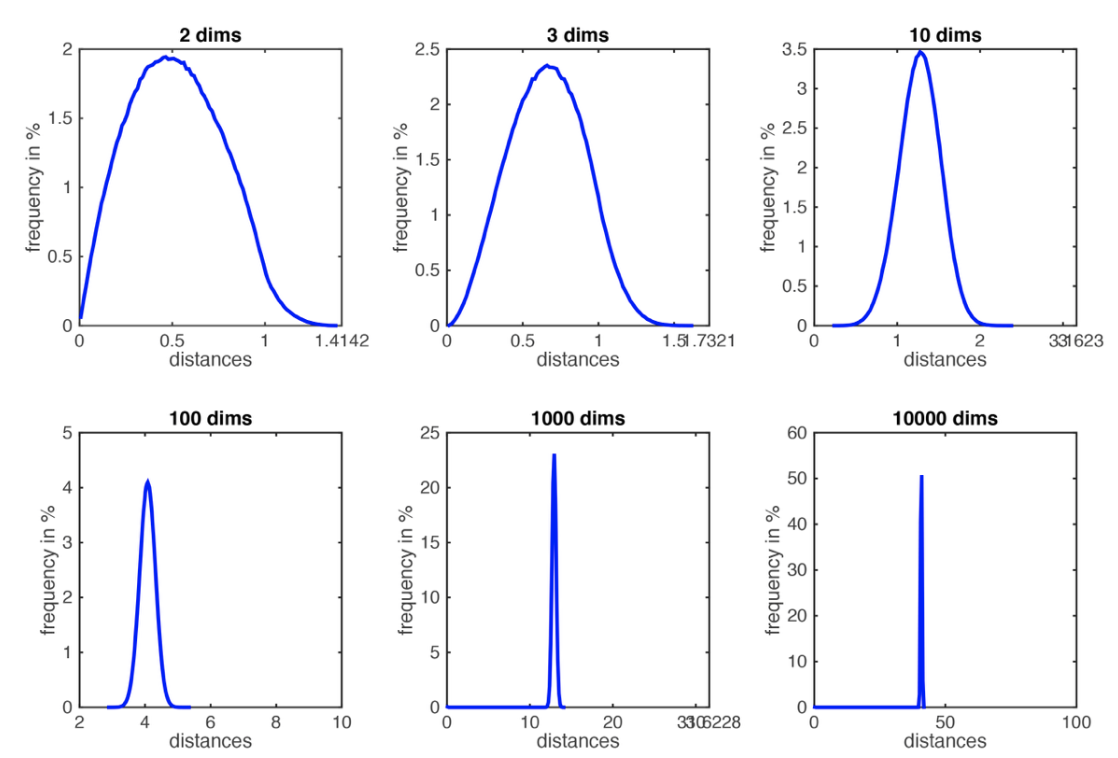

사진을 보시면 데이터의 분포가 dim이 커질수록 좁아지고, 거리를 이용한 구분이 의미를 잃는 것이 보입니다.

간단한 해결법은 저차원(hyperplanes)에 mapping 하거나, 혹은 저차원 data에도 적용 가능한 data만 적용하거나 그냥 높은 차원의 data에는 사용하지 않는 것 입니다..!

(관련 내용은 가능하다면 추후에 서술하겠습니다..!)

정리

k-NN is a simple and effective classifier if distances reliably reflect a semantically meaningful notion of the dissimilarity. (It becomes truly competitive through metric learning)

As n → ∞, k-NN becomes provably very accurate, but also very slow.

As d ≫ 0, points drawn from a probability distribution stop being similar to each other, and the k NN assumption breaks down.

참고자료 및 출처

https://www.youtube.com/playlist?list=PLl8OlHZGYOQ7bkVbuRthEsaLr7bONzbXS

https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote02_kNN.html

위 포스트는 코넬대학교 강의 CS4780과 그 강의 자료를 정리한 내용입니다.