퍼셉트론

지능 시스템을 위한 기계학습

"기계학습"
"ML"
강의: CORNELL CS4780 "Machine Learning for Intelligent Systems"

해당 포스트는 코넬대학교 CS4780과 그 강의 자료를 정리한 내용입니다.

---

이 글을 쓰게 된 계기

기계학습에 대한 전반적인 이해와 그 알고리즘을 학습해봅시다!

---

So, what is Perceptron?

Perceptron은 갈라치기 싸움입니다!

자 이제 왜 제가 이런 설명을 했는지 Perceptron에 대해서 알아보며 이해해봅시다!!

---

기본: 두가지 가정

퍼셉트론에 대하여 설명하기에 앞서 이 알고리즘을 위해서는 두 가지 가정을 짚고 넘어가야 합니다.

Assumptions

1. Binary classification (i.e. $y_i \in \{-1,+1\}$)
2. Data is linearly separable

   $\mathbf{w}^*$ 은 결과 벡터입니다.

---

이제 분류를 해볼까요?

우리는 분류를 hyperplane을 이용하여 할 것 입니다!

$h(x_i) = \text{sign}(\mathbf{w}^T x_i + b)$

수식설명: $\mathbf{w}^T x_i + b = 0$ 이 되는 $x_i$들의 집합이 $h(x_i)$가 됩니다! -> 이것이 초평면, hyperplane입니다!

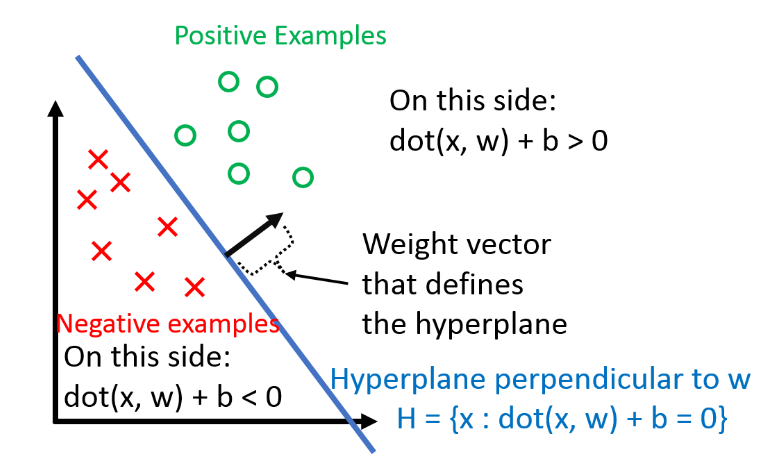
$b$ 는 bias term 입니다! (bias term이 없다면 $w$ 가 만드는 hyperplane은 항상 원점을 지날 것입니다! 이해가 가지 않는다면 직교하는 두 벡터를 생각해보면 좋을 것 같습니다.). $b$만 따로 다루는 것은 드럽기 때문에, 우리는 feature vector $w$로 '흡수' 시킬것입니다! 단순히 하나의 차원을 늘리는 방법으로요!

그렇게 한다면 아래와 같이 표현이 가능합니다!

매우 간단해졌죠? 아래는 시각적으로 보여준 자료입니다!

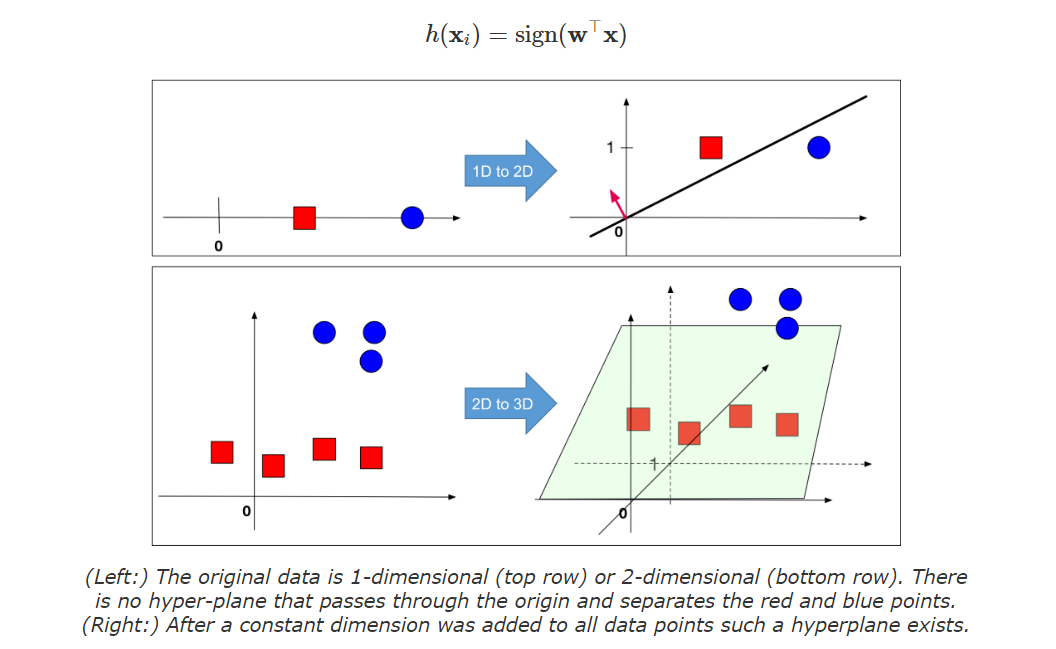
앞으로의 수식 전개를 위한 important factor!

$y_i(\mathbf{w}^T x_i) > 0 \Longleftrightarrow x_i \text{ is classified correctly}$

but, why?

my 분석 : inner product의 정의에 의하여 코사인에 의해 음, 양이 결정됩니다. 이때 index가 음에는 -1이 곱해지고, 양에는 1이 곱해져서 위와같은 식이 나옵니다. 또한 초평면 위의 점은 미분류로 처리하기 때문에 위 수식이 나왔다고 생각합니다.

---

So... let's see the algorithm...

Perceptron Algorithm

목표: w를 찾습니다.

w = 0 
while True
	m = 0
    for every (x,y) in D
    	if y(w^t)(x) <= 0 #실패시
        	w = w + yx	#업데이트
            m = m+1	#실패했다고 마킹
    if m==0:
    	break    

시각적 설명

---

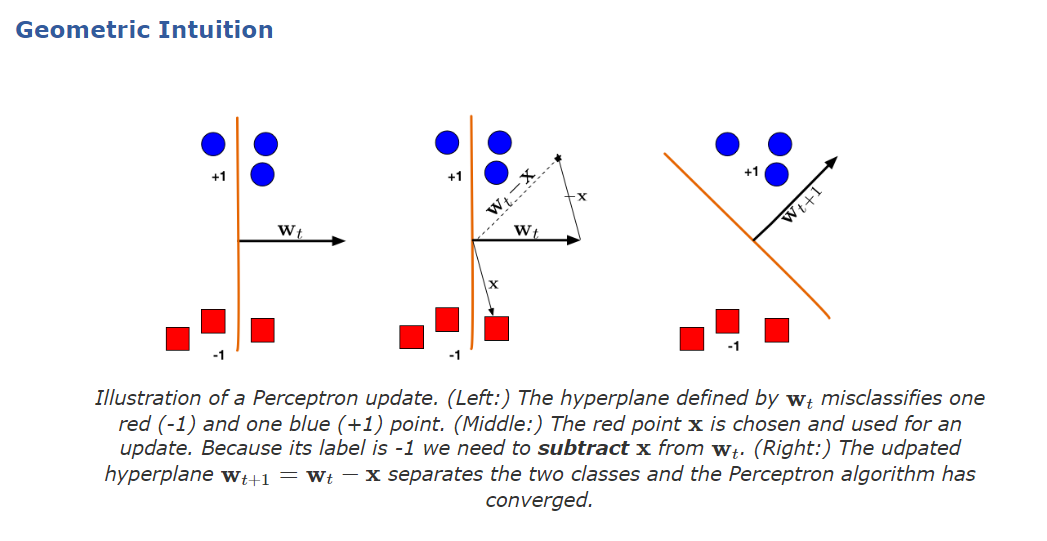
Then, how? 어떻게 결과값이 나온다고 장담하죠?

퍼셉트론 알고리즘의 결과는 단 하나입니다!

hyperplane!

우리는 이미 가정으로 분리 가능하다는 전제를 깔아두었기 때문에 전제가 위반되지 않는다면 hyperplane을 상수시간 내에 찾아낼 수 있음(Convergence)을 증명하면 충분합니다!

단계

1. 가정
2. rescaling with margin 계산(초평면으로 부터의 최단거리의 point)
3. 증명

1. 가정 단계

$\text{Suppose } \exists \mathbf{w}^* \text{ such that } y_i(x_i^⊤ \mathbf{w}^*) > 0 \quad \forall (x_i, y_i) \in D.$

설명: 이건 그냥 데이터의 분할 가능성을 의미합니다. 그렇다면 그러한 초평면이 존재할 것이라고 가정하는 것입니다!

2. rescaling with margin 계산(초평면으로 부터의 최단거리의 point)

$\|\mathbf{w}^*\| = 1 \quad \text{and} \quad \|x_i\| \leq 1 \quad \forall x_i \in D$

$\text{Margin } \gamma \text{ of the hyperplane } \mathbf{w}^* \text{ as } \gamma = \min_{(x_i,y_i) \in D} y_i |x_i^T \mathbf{w}^*|.$

이때 $\|x_i\| \leq 1$ 를 만드는 방법은

$x_i = x_i / \argmax_{x_i \in D} y_i |x_i^T \mathbf{w}^*|$

그렇다면 결과물은 단위원이 될 것입니다!

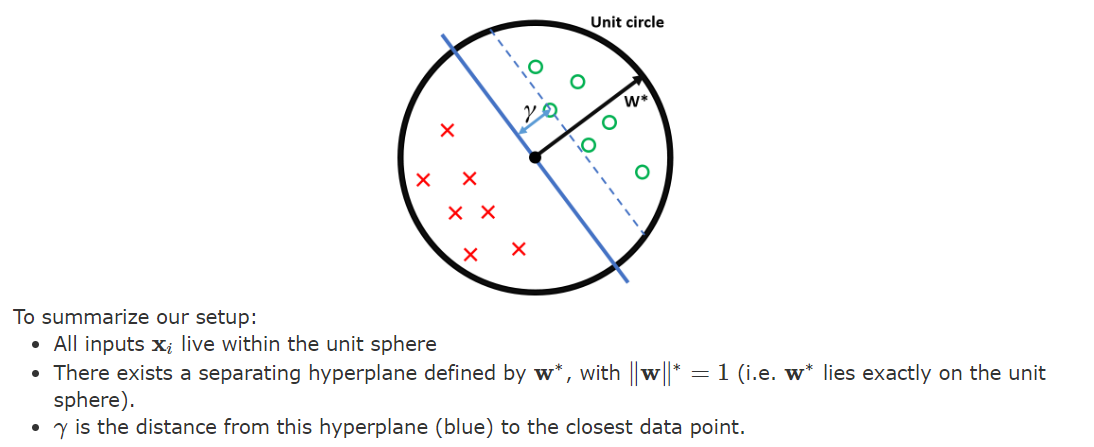
3. 증명

Theorem(목표): If all of the above holds, then the Perceptron algorithm makes at most $1/gamma^2$ mistakes.

증명 진행 기본.

두가지 fact :

1. $y(x^⊤\mathbf{w})≤0$ : This holds because $x$ is misclassified by $w$

• otherwise we wouldn't make the update.(업데이트 상황 가정)

2. $y(x^⊤\mathbf{w}^∗)>0$ : This holds because $\mathbf{w}^∗$ is a separating hyper-plane and classifies all points correctly.

증명 진행

1. $\mathbf{w}^⊤\mathbf{w}^*$ 측면에서 update 영향 측정

   $(\mathbf{w} + y \mathbf{x})^⊤ \mathbf{w}^* = \mathbf{w}^⊤ \mathbf{w}^* + y (\mathbf{x}^⊤ \mathbf{w}^*) \geq \mathbf{w}^⊤ \mathbf{w}^* + \gamma$

   (because $y (\mathbf{x}^⊤ \mathbf{w}^*) \geq \gamma$)

그럼 이것은 $\mathbf{w}^⊤\mathbf{w}$ 의 증가는 최소 $\gamma$만큼 이루어 진다는 뜻 입니다.

2. $\mathbf{w}^⊤\mathbf{w}$ 측면에서 update 영향 측정

   $(\mathbf{w} + y \mathbf{x})^T (\mathbf{w} + y \mathbf{x}) = \mathbf{w}^T \mathbf{w} + 2 y (\mathbf{w}^T \mathbf{x}) + y^2 (\mathbf{x}^T \mathbf{x}) \leq \mathbf{w}^T \mathbf{w} + 1$

   (because $2y (\mathbf{w}^T \mathbf{x}) < 0$ and $0 ≤ y^2 (\mathbf{x}^T \mathbf{x})≤1$)

후자의 경우 y제곱은 1이고, xTx는 Rescaling에 의하여 1보다 작거나 같으므로...

그렇다면 이것은 $\mathbf{w}^⊤\mathbf{w}$의 증가는 최대 $1$ 만큼만 이루어진다는 뜻 입니다.

3. $M$번 시행 후 결과 확인
   2가지 inequalities
   (1) $\mathbf{w}^⊤\mathbf{w}^* ≥ M\gamma$
   (2) $\mathbf{w}^⊤\mathbf{w} ≤ M$

   결과본**:

   2번줄 설명

   line 2: 내적의 정의 이용 + w*의 norm이 1이라는 점 이용

Quiz

$\mathbf{w}^*$는 여러개가 있을 수 있습니다, 그렇다면 어떤 $\mathbf{w}^*$가 선택될까요?

---

결론

방법은 간단하지만 증명과정에서 지려버리는 알고리즘이네요...

정리

참고자료 및 출처

https://www.youtube.com/playlist?list=PLl8OlHZGYOQ7bkVbuRthEsaLr7bONzbXS

https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote02_kNN.html

위 포스트는 코넬대학교 강의 CS4780과 그 강의 자료를 정리한 내용입니다.