💡 Number of Island
Given an m x n 2D binary grid grid which represents a map of '1's (land) and '0's (water), return the number of islands.
An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example 1:
Input: grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
Output: 1Example 2:
Input: grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
Output: 3Solution

설명 보고 코드 잘 짯다가,
dfs에서 i와 j가 범위 밖으로 벗어나는 케이스를 포함을 안시켜줘서 애먹다 포함시켜 줬다
class Solution {
public:
int numIslands(vector<vector<char>>& grid) {
int m = grid.size();
int n = grid[0].size();
int result = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == '1') {
dfs(grid, i, j, m, n);
// when dfs is done on the first found land,
// it finished finding an island
// and also marked 0 to visited island
result++;
}
}
}
return result;
}
private:
void dfs(vector<vector<char>> &grid, int i, int j, int m, int n) {
if (i >= m || j >= n || i < 0 || j < 0 || grid[i][j] == '0') return;
grid[i][j] = '0';
// check vertical
dfs(grid, i+1, j, m, n);
dfs(grid, i-1, j, m, n);
// check left and right
dfs(grid, i, j+1, m, n);
dfs(grid, i, j-1, m, n);
}
};💡Max Area of Island
You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.
The area of an island is the number of cells with a value 1 in the island.
Return the maximum area of an island in grid. If there is no island, return 0.
Example 1:
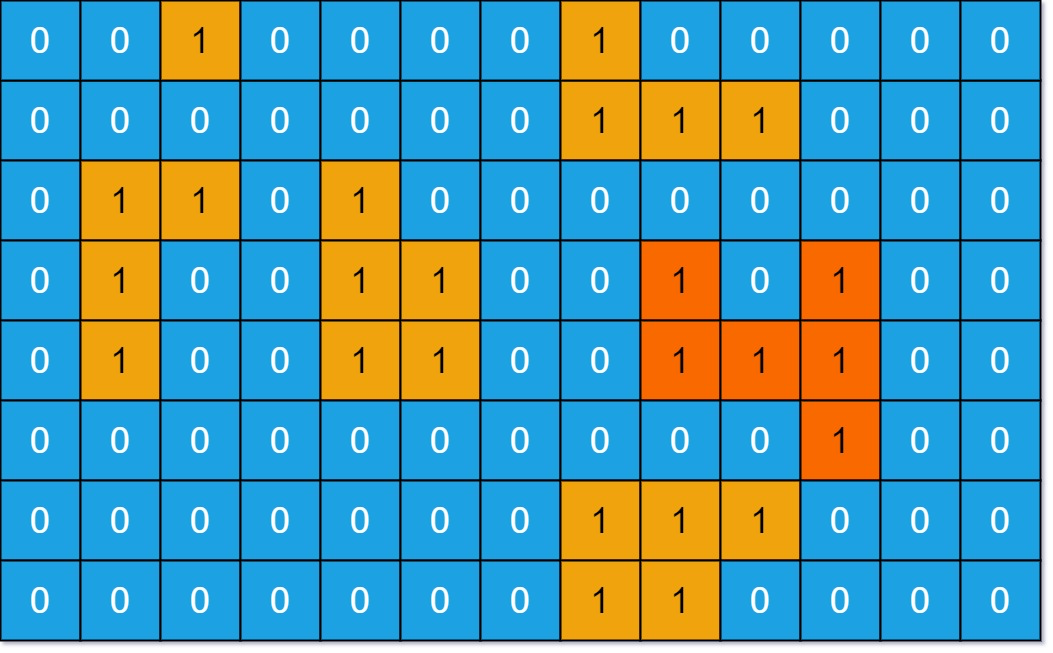
Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
Output: 6
Explanation: The answer is not 11, because the island must be connected 4-directionally.Example 2:
Input: grid = [[0,0,0,0,0,0,0,0]]
Output: 0Solution
바로 전 문제에서 썼던 알고리즘을 사용하여 area를 계산하는 부분만 추가해주면 된다
class Solution {
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
int curr = 0;
int result = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
dfs(grid, i, j, m, n, curr);
// when dfs is done on the first found land,
// it finished finding an island
// and also marked 0 to visited island
result = max(result, curr);
curr = 0;
}
}
}
return result;
}
private:
void dfs(vector<vector<int>> &grid, int i, int j, int m, int n, int &curr) {
if (i >= m || j >= n || i < 0 || j < 0 || grid[i][j] == 0) return;
grid[i][j] = 0;
curr += 1;
// check vertical
dfs(grid, i+1, j, m, n, curr);
dfs(grid, i-1, j, m, n, curr);
// check diagonal
dfs(grid, i, j+1, m, n, curr);
dfs(grid, i, j-1, m, n, curr);
}
};💡 Number of Connected Components in an Undirected Graph
촴나 이건 유료문제 ㅡ,.ㅡ
하지만 구글링하면 무슨문제인줄 유추할 수 있지롱
그리고 이 문제 뭔가 중요해 보인당 ,,
Given n nodes labeled from 0 to n - 1 and a list of undirected edges (each edge is a pair of nodes), write a function to find the number of connected components in an undirected graph.
Example 1:
0 3
| |
1 --- 2 4
Given n = 5 and edges = [[0, 1], [1, 2], [3, 4]], return 2.Example 2:
0 4
| |
1 --- 2 --- 3
Given n = 5 and edges = [[0, 1], [1, 2], [2, 3], [3, 4]], return 1.🙆🏻♀️ Connected Components
직접 그린 그림으로 설명하자면 이렇다
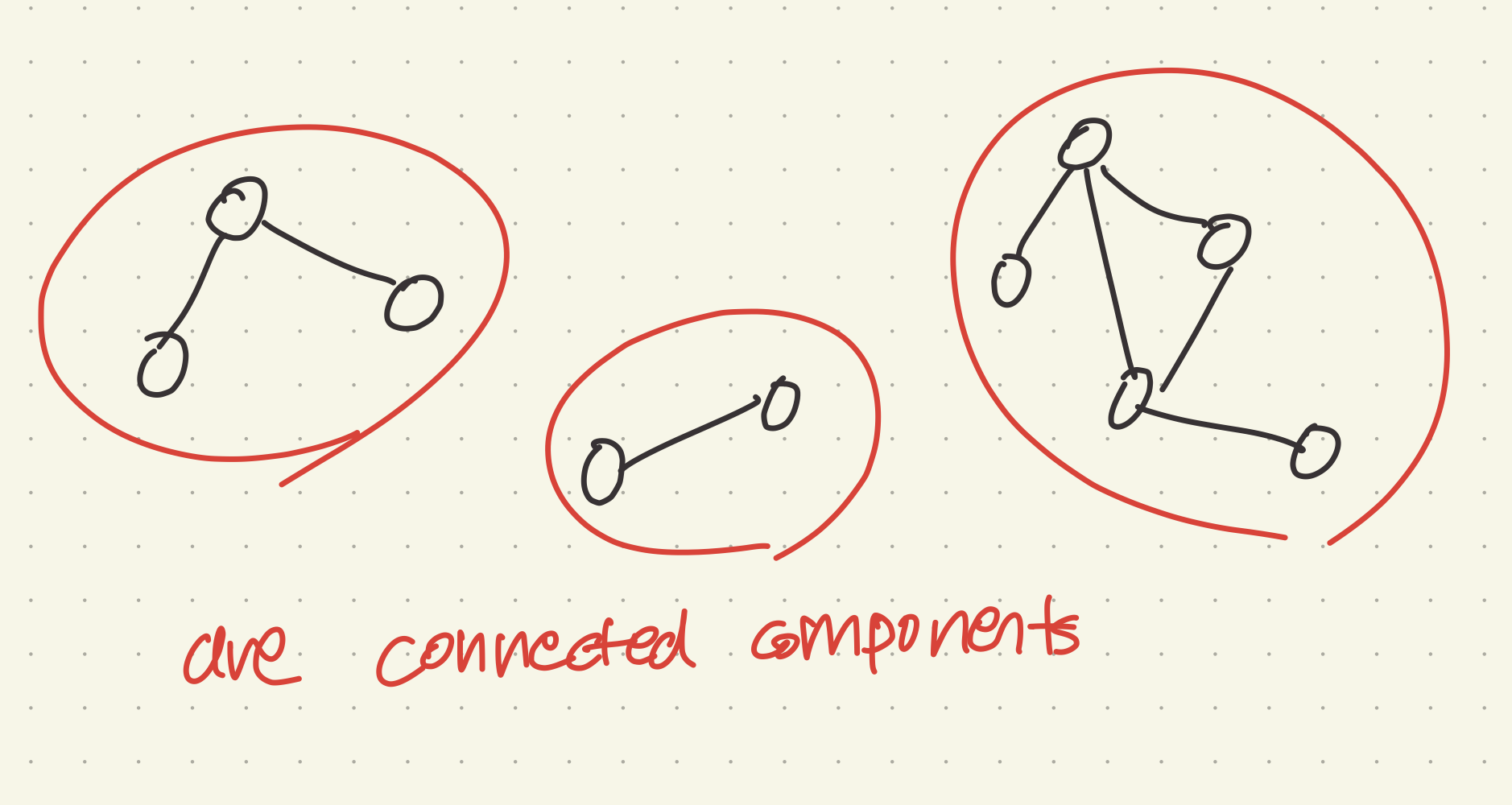
말로 정의하자면,
- connected components에 속한 모든 node를 연결하는 path가 있어야 한다.
- 또, 다른 connected components에 속한 node와 연결하는 path가 있으면 안된다.
- connected components를 찾는 방법은 BFS, DFS 탐색을 이용하면 된다.
- BFS, DFS를 시작하면 시작 node로부터 도달 가능한 모든 node들이 하나의 connected component가 된다.
- 다음에, 방문하지 않은 node을 선택해서 다시 탐색을 시작하면 그 node을 포함하는 connected component가 구해진다.
- 이 과정을 그래프 상의 모든 node가 방문될 때까지 반복하면 그래프에 존재하는 모든 connected component들을 찾을 수 있다.
Solution
node의 갯수와 edges가 인풋으로 들어온다
이 두개의 인풋을 활용해 graph를 2d array로 표현하자
그리고 방문한 node를 표시해두기 위한 visited 벡터도 생성한다
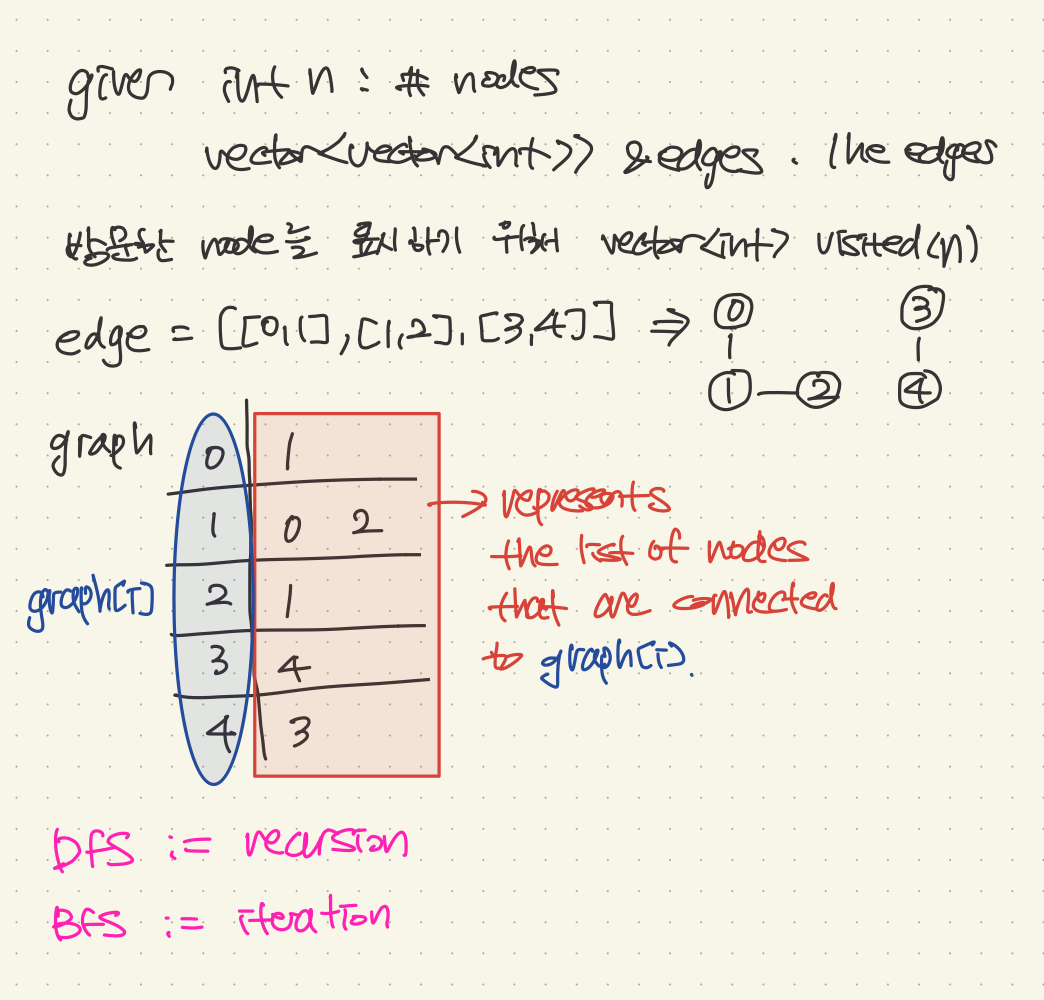
DFS
class Solution {
public:
int countComponents(int n, vector<pair<int, int>>& edges) {
vector<vector<int>>graph(n);
vector<int>visited(n);
//construct a graph so that
// graph[i] returns the list of nodes that are connected to node i
for (auto x: edges){
graph[x.first].push_back(x.second);
graph[x.second].push_back(x.first);
}
int num_connected_components = 0;
for (int i = 0; i < n; i++){
// 이미 방문한 node이면 넘어가자
if(visited[i])
continue;
// 처음으로 만나는 node를 마주친다면 그건 새로운 connected component라는 뜻
num_connected_components++;
// DFS를 이용해서 지금 node에서 퍼져 나갈 수 있는 곳까지 나가면서
// 방문하는 node들은 재방문하지 않도록 표시하자
DFS(graph, i, visited);
}
return num_connected_components;
}
void DFS(vector<vector<int>>& graph, int i, vector<int>& visited){
// 이미 방문한 node라면 넘어가자
if(visited[i]) return;
// 처음보는 node라면 방문했다고 표시해주자
visited[i] = 1;
// graph[i]로 현재 node에 연결된 node들의 리스트를 불러올 수 있었다
// 현재 node에 연결된 node 중에 아직 방문하지 않았던 node에게 DFS를 실행해주자
for(auto neigh: graph[i])
if(!visited[neigh])
DFS(graph, neigh, visited);
}
};BFS
// BFS
class Solution {
public:
int countComponents(int n, vector<pair<int, int>>& edges) {
vector<vector<int>>graph(n);
vector<int>visited(n);
// DFS에서 생성했던 graph와 같다
for (auto x: edges) {
graph[x.first].push_back(x.second);
graph[x.second].push_back(x.first);
}
int num_connected_components = 0;
for (int i = 0; i < n; i++) {
// 이미 방문한 node면 넘어가자
if (visited[i]) continue;
// 처음으로 만나는 node를 마주친다면 그건 새로운 connected component라는 뜻
num_connected_components++;
// dequeue는 양쪽 끝에서 접근 가능한 queue
// (근데 이거 일반 queue써도 되겠당 ,,)
deque<int>q;
// 지금 만난 node를 queue에 넣어주고,
q.push_back(i);
// queue에 있는 node들을 방문해주자
while (!q.empty()) {
// queue에 저장한 node중 맨 앞에 있는 애를 불러와서,
int node = q.front();
q.pop_front();
// 방문했다고 표시해주고,
visited[node] = 1;
// 해당 node의 이웃들 중에 이미 방문하지 않은 node를 queue에 push한다
/*
** DFS와 다른 여기서 나온다
**
** 방문하지 않은 노드를 만나면 바로 그 노드에 대한 search를 해주는게 아니라
** queue에 저장해놨다가 나중에 차례가 오면 search를 진행한다!
** 이래서 level by level인가보다.
*/
for (auto neigh: graph[node])
if (!visited[neigh])
q.push_back(neigh);
}
}
return num_connected_components;
}
};💡 Clone Graph
Given a reference of a node in a connected undirected graph.
Return a deep copy (clone) of the graph.
Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.
class Node {
public int val;
public List<Node> neighbors;
}Solution
DFS
class Solution {
public:
Node* cloneGraph(Node* node) {
// we need to mark visited nodes
// so that we don't create nodes over and over again
// this will cause stack overflow!
// clones.first = orig node
// clones.second = clone node
unordered_map<Node *, Node *> clones;
if (node == NULL) return NULL;
return dfs(node, clones);
}
private:
Node *dfs(Node *node, unordered_map<Node *, Node *> &clones) {
// if we already cloned this node
if (clones.find(node) != clones.end())
// return the clone
return clones[node];
// if the clone doesn't exist yet,
// then clone this node
Node *clone = new Node(node->val);
// don't forget to add the clone to the clones map
clones[node] = clone;
// loop through the neighbours of the original node
int num_neighbours = node->neighbors.size();
for (int i = 0; i < num_neighbours; i++) {
// clone each neighbour nodes and push to clone's neighbour list
clone->neighbors.push_back(dfs(node->neighbors[i], clones));
}
return clone;
}
};BFS
class Solution {
public:
Node* cloneGraph(Node* node) {
// we need to mark visited nodes
// clones.first = orig node
// clones.second = clone node
unordered_map<Node *, Node *> clones;
if (node == NULL)
return NULL;
// create the clone of the node here
// so that later in the while loop, it doesn't cause seg fault
Node *copy = new Node(node->val);
clones[node] = copy;
// this queue only stores the original node
queue<Node *> q;
q.push(node);
while (!q.empty()) {
// pop the front node in the queue
Node *curr = q.front();
q.pop();
// the neighbours
int num_neighbours = curr->neighbors.size();
for (int i = 0; i < num_neighbours; i++) {
// pointer to this original neighbour
Node *orig_neighbour = curr->neighbors[i];
// if the clone of the neighbour does NOT exists,
// create the clone of the original and map it
// and add the original to the queue so that we can clone it later
if (clones.find(orig_neighbour) == clones.end()) {
clones[orig_neighbour] = new Node(orig_neighbour->val);
q.push(orig_neighbour);
}
// push the clone to the clone's neighbours list
clones[curr]->neighbors.push_back(clones[orig_neighbour]);
}
}
return copy;
}
};BFS는 진짜 헷갈린당, ,, ㅜ
DFS 와 BFS의 time complexity는 둘 다 O(#nodes + #edges) 이다
어떤 예제에서 그래프를 써야할지 실생활 예제를 보자
💡 Course Schedule
There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course bi first if you want to take course ai.
For example, the pair [0, 1], indicates that to take course 0 you have to first take course 1.
Return true if you can finish all courses. Otherwise, return false.
Example 1:
Input: numCourses = 2, prerequisites = [[1,0]]
Output: true
Explanation: There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.Example 2:
Input: numCourses = 2, prerequisites = [[1,0],[0,1]]
Output: false
Explanation: There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.Solution
courses가 node, prerequisites를 edge로 볼 수 있겠다
문제가 잘 이해가 안갔는데,,
그니깐
numCourses 개수의 코스를 들어야 하고, prerequisites는 그 코스들에 대해서 prerequisites을 표현해 놓은거고,,,
모든 코스들을 다 들어야 하니깐 prerequisites를 고려해서 다 들을 수 있는 강의들인지 확인하라는 문제같다
prerequisite chain이 cycle이라면 코스를 다 듣기는 불가능 하므로 false,,
다시말해 cycle이 있는지 체크하라는 문제넹
이미 방문 했던 node를 다시 방문한다면 그것은 cycle이니까 false를 return하면 되겠군,,

class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
unordered_map<int, vector<int>> pr_map(numCourses);
int m = prerequisites.size();
for (int i = 0; i < m; i++) {
pr_map[prerequisites[i][0]].push_back(prerequisites[i][1]);
}
unordered_set<int> visited;
for (int i = 0; i < numCourses; i++) {
if (!dfs(i, pr_map, visited))
//when dfs returns false, return false as answer
return false;
}
return true;
}
private:
bool dfs(int cur_course, unordered_map<int, vector<int>> &pr_map, unordered_set<int> &visited) {
if (visited.find(cur_course) != visited.end())
// when this course was already visited before
return false;
if (pr_map[cur_course].empty())
// empty prerequisite list means no cycle
return true;
visited.insert(cur_course);
// for each prerequisite courses
for (int i = 0; i < pr_map[cur_course].size(); i++) {
int next_course = pr_map[cur_course][i];
// run dfs on the prerequisite course
if (!dfs(next_course, pr_map, visited))
return false;
}
// dfs from cur_course was done without returning false:
// we clear the prerequisite course list from the map
// to indicate that this course do not cause any cycle
// (to optimize when this course is visited again later in another dfs journey)
pr_map[cur_course].clear();
// also remove from visited
visited.erase(cur_course);
return true;
}
};💡 Course Schedule II
There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course bi first if you want to take course ai.
For example, the pair [0, 1], indicates that to take course 0 you have to first take course 1.
Return the ordering of courses you should take to finish all courses. If there are many valid answers, return any of them. If it is impossible to finish all courses, return an empty array.
Example 1:
Input: numCourses = 2, prerequisites = [[1,0]]
Output: [0,1]
Explanation: There are a total of 2 courses to take. To take course 1 you should have finished course 0. So the correct course order is [0,1].Example 2:
Input: numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
Output: [0,2,1,3]
Explanation: There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
So one correct course order is [0,1,2,3]. Another correct ordering is [0,2,1,3].Example 3:
Input: numCourses = 1, prerequisites = []
Output: [0]Solution
쫌 헷갈린당
조심해서 보자!
class Solution {
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
vector<int> result;
// construct a map: {course # -> prerequisite list}
unordered_map<int, vector<int>> prs(numCourses);
int pr_size = prerequisites.size();
for (int i = 0; i < pr_size; i++) {
prs[prerequisites[i][0]].push_back(prerequisites[i][1]);
}
// if there is a cycle, then it is imposible
// so we need a vector 'visited' to check visited courses
unordered_set<int> visited;
// need to keep track of which courses are taken
unordered_set<int> taken;
// for each course,
for (int i = 0; i < numCourses; i++) {
if (!dfs(i, prs, visited, taken, result)) {
// dfs return false meaning there is a cycle -> impossible
return {};
}
// dfs return true meaning
// 1. we were able to take the course
// 2. course was already in the result
}
return result;
}
private:
bool dfs(int cur_course, unordered_map<int, vector<int>> &prs,
unordered_set<int> &visited, unordered_set<int> &taken, vector<int> &result) {
if (visited.find(cur_course) != visited.end()) {
// cycle
return false;
}
if (taken.find(cur_course) != taken.end()) {
// course already in the result list
return true;
}
visited.insert(cur_course);
// for each prerequisites of this course
int pr_size = prs[cur_course].size();
for (int i = 0; i < pr_size; i++) {
int next_course = prs[cur_course][i];
if (!dfs(next_course, prs, visited, taken, result)) {
// if dfs on prerequisite course is false
return false;
}
}
visited.erase(cur_course);
taken.insert(cur_course);
result.push_back(cur_course);
return true;
}
};💡 Pacific Atlantic Water Flow
There is an m x n rectangular island that borders both the Pacific Ocean and Atlantic Ocean. The Pacific Ocean touches the island's left and top edges, and the Atlantic Ocean touches the island's right and bottom edges.
The island is partitioned into a grid of square cells. You are given an m x n integer matrix heights where heights[r][c] represents the height above sea level of the cell at coordinate (r, c).
The island receives a lot of rain, and the rain water can flow to neighboring cells directly north, south, east, and west if the neighboring cell's height is less than or equal to the current cell's height. Water can flow from any cell adjacent to an ocean into the ocean.
Return a 2D list of grid coordinates result where result[i] = [ri, ci] denotes that rain water can flow from cell (ri, ci) to both the Pacific and Atlantic oceans.
Example 1:
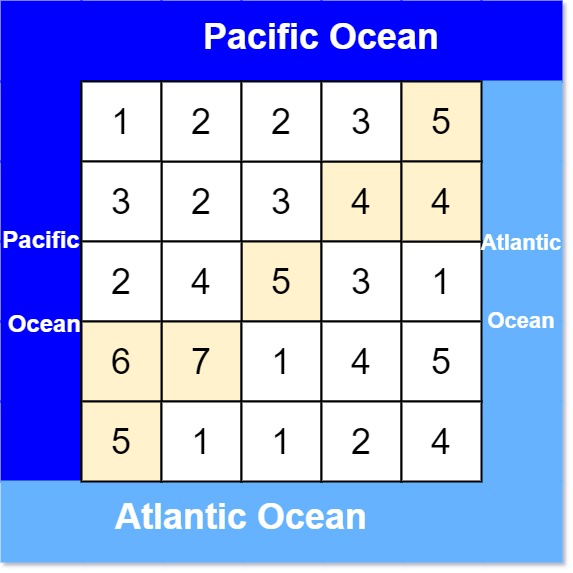
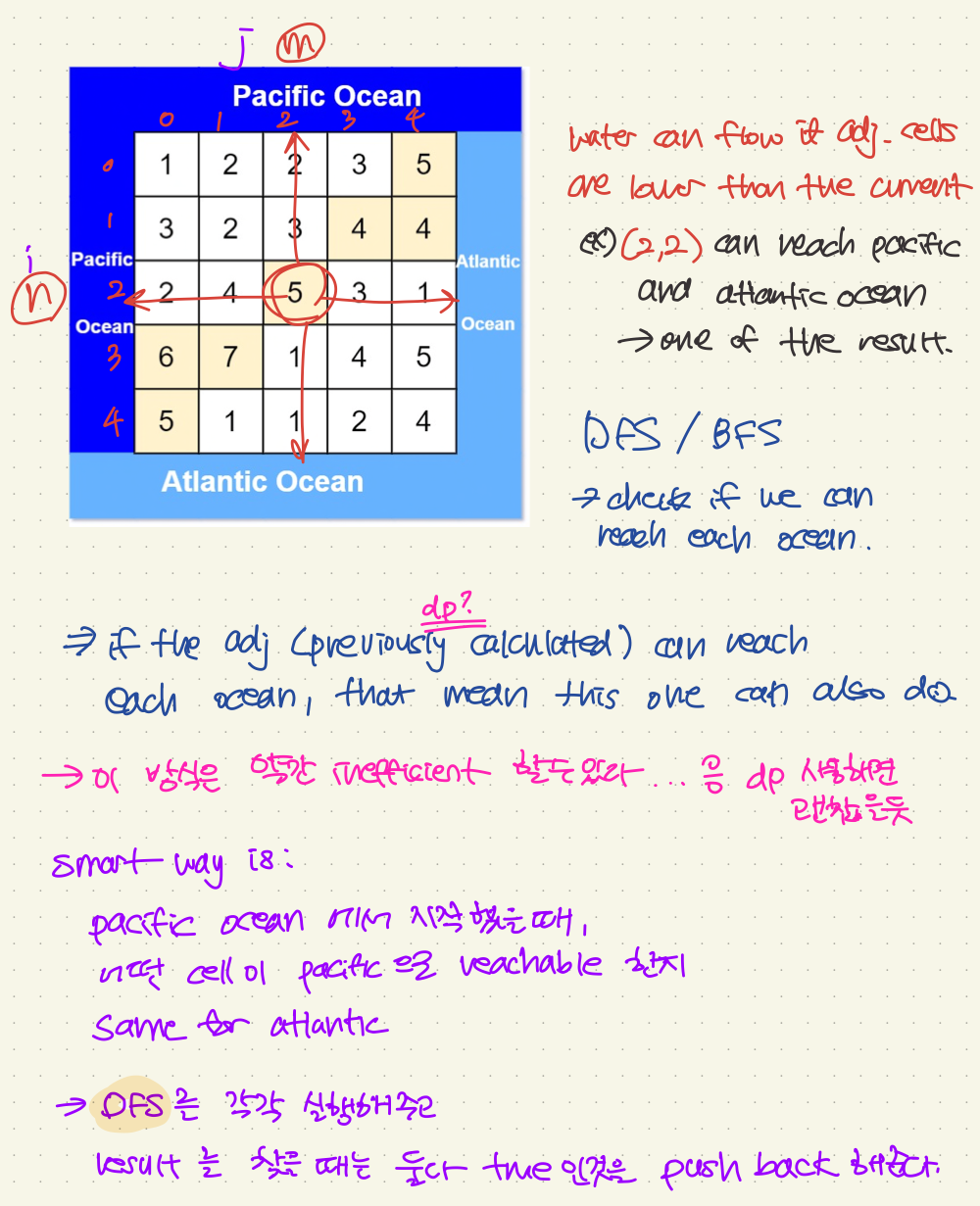
Input: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
Output: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
Explanation: The following cells can flow to the Pacific and Atlantic oceans, as shown below:
[0,4]: [0,4] -> Pacific Ocean
[0,4] -> Atlantic Ocean
[1,3]: [1,3] -> [0,3] -> Pacific Ocean
[1,3] -> [1,4] -> Atlantic Ocean
[1,4]: [1,4] -> [1,3] -> [0,3] -> Pacific Ocean
[1,4] -> Atlantic Ocean
[2,2]: [2,2] -> [1,2] -> [0,2] -> Pacific Ocean
[2,2] -> [2,3] -> [2,4] -> Atlantic Ocean
[3,0]: [3,0] -> Pacific Ocean
[3,0] -> [4,0] -> Atlantic Ocean
[3,1]: [3,1] -> [3,0] -> Pacific Ocean
[3,1] -> [4,1] -> Atlantic Ocean
[4,0]: [4,0] -> Pacific Ocean
[4,0] -> Atlantic Ocean
Note that there are other possible paths for these cells to flow to the Pacific and Atlantic oceans.Example 2:
Input: heights = [[1]]
Output: [[0,0]]
Explanation: The water can flow from the only cell to the Pacific and Atlantic oceans.Solution
현재 cell에서 각 ocean으로 갈 수 있는지를 알아보는 문제인데
생각을 약간 바꿔서 각 ocean이 각 cell로 갈 수 있는지로 flip 해서 생각해보면 좀 더 쉽다!
(대신 컨디션이 height이 더 작아야 하는 것에서 height이 더 큰지 체크해야한다! (flip))
class Solution {
public:
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
vector<vector<int>> result;
int n = heights.size();
int m = heights[0].size();
// each cell represents whether it is reachable from pacific ocean
vector<vector<bool>> pacific(n, vector<bool>(m));
// each cell represents whether it is reachable from atlantic ocean
vector<vector<bool>> atlantic(n, vector<bool>(m));
// to mark the cells that are reachable from pacific/atlantic ocean
for (int j = 0; j < m; j++) {
// top row (attached to the pacific ocean)
dfs(heights, pacific, 0, j, n, m);
// bottom row (attached to the atlantic ocean)
dfs(heights, atlantic, n-1, j, n, m);
}
for (int i = 0; i < n; i++) {
// left row (attached to the pacific ocean)
dfs(heights, pacific, i, 0, n, m);
// right row (attached to the atlantic ocean)
dfs(heights, atlantic, i, m-1, n, m);
}
// only push the cells that are reachable from both pacific and atlantic
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (pacific[i][j] && atlantic[i][j])
result.push_back({i ,j});
}
}
return result;
}
private:
void dfs(vector<vector<int>>& heights, vector<vector<bool>> &visited, int i, int j, int n, int m) {
visited[i][j] = true;
// check if it can travel upward
// condition 1. upward is not OOB
// 2. didn't visited the upward cell yet
// 3. upward cell >= current cell **WATCH OUT**
if (0 < i && !visited[i-1][j] && heights[i-1][j] >= heights[i][j])
dfs(heights, visited, i-1, j, n, m);
// similary check downward
if (i < n-1 && !visited[i+1][j] && heights[i+1][j] >= heights[i][j])
dfs(heights, visited, i+1, j, n, m);
// similary check left
if (0 < j && !visited[i][j-1] && heights[i][j-1] >= heights[i][j])
dfs(heights, visited, i, j-1, n, m);
// similary check right
if (j < m-1 && !visited[i][j+1] && heights[i][j+1] >= heights[i][j])
dfs(heights, visited, i, j+1, n, m);
}
};💡 Surrounded Regions
Given an m x n matrix board containing 'X' and 'O', capture all regions that are 4-directionally surrounded by 'X'.
A region is captured by flipping all 'O's into 'X's in that surrounded region.
Example 1:
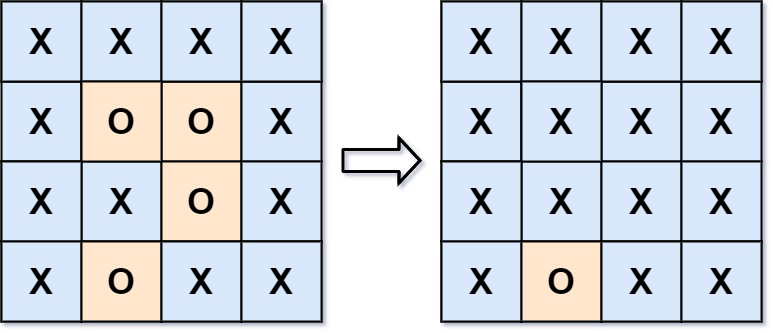
Input: board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
Output: [["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
Explanation: Notice that an 'O' should not be flipped if:
- It is on the border, or
- It is adjacent to an 'O' that should not be flipped.
The bottom 'O' is on the border, so it is not flipped.
The other three 'O' form a surrounded region, so they are flipped.Example 2:
Input: board = [["X"]]
Output: [["X"]]Solution

class Solution {
public:
void solve(vector<vector<char>>& board) {
int n = board.size();
int m = board[0].size();
// 1. scan through the boarder and find 'O'
for (int j = 0; j < m; j++) {
// top row
if (board[0][j] == 'O')
dfs(board, 0, j, n, m);
// bottom row
if (board[n-1][j] == 'O')
dfs(board, n-1, j, n, m);
}
for (int i = 0; i < n; i++) {
// left col
if (board[i][0] == 'O')
dfs(board, i, 0, n, m);
// right col
if (board[i][m-1] == 'O')
dfs(board, i, m-1, n, m);
}
// 2. completed dfs
// 3. iterate and change every 'O' into 'X', they are surrounded
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (board[i][j] == 'O')
board[i][j] = 'X';
}
}
// 4. change 'T' to 'O' for result
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (board[i][j] == 'T')
board[i][j] = 'O';
}
}
}
private:
void dfs(vector<vector<char>>& board, int i, int j, int n, int m) {
// 2. run DFS on unsurrounded 'O'
// - change this 'O' into 'T' to mark it is unsurrounded
board[i][j] = 'T';
// run DFS on 'O' that is connected to this 'O'
// up
if (0 < i && board[i-1][j] == 'O')
dfs(board, i-1, j, n, m);
// down
if (i < n-1 && board[i+1][j] == 'O')
dfs(board, i+1, j, n, m);
// left
if (0 < j && board[i][j-1] == 'O')
dfs(board, i, j-1, n, m);
// right
if (j < m-1 && board[i][j+1] == 'O')
dfs(board, i, j+1, n, m);
}
};💡 Rotting Oranges
You are given an m x n grid where each cell can have one of three values:
0 representing an empty cell,
1 representing a fresh orange, or
2 representing a rotten orange.
Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.
Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.
Example 1:
Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4Example 2:
Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.Example 3:
Input: grid = [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.Solution
DFS가 아닌 BFS로 이문제를 풀어야 한다!!
이유: we need to calculate time and oragnes can be simultaneously become rotten!!
class Solution {
public:
int orangesRotting(vector<vector<int>>& grid) {
int n = grid.size();
int m = grid[0].size();
queue<pair<int, int>> q; // queue of rotten oranges
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 2)
q.push({i, j});
}
}
int time = -1;
vector<pair<int,int>> neighbours = {{-1,0}, {1,0}, {0,-1}, {0,1}}; // up, down, left, right
while (!q.empty()) {
// need to track current q (for THIS time interval)
// oranges for current time interval
queue<pair<int, int>> curr_q = q;
// reset q: 여기엔 이제 next time interval을 위한 orange(the neighbours)들을 넣어준다
q = queue<pair<int, int>>();
while (!curr_q.empty()) {
pair<int, int> orange = curr_q.front();
curr_q.pop();
// check the neighbours
for (auto neigh : neighbours) {
int i = orange.first + neigh.first;
int j = orange.second + neigh.second;
if (i >= 0 && i < n && j >= 0 && j < m && grid[i][j] == 1) { //if neighbour is fresh
// to mark this neighbour is already in the queue, mark it was rotten
grid[i][j] = 2;
q.push({i, j}); //this fresh neighbour will be executed in the next time interval
}
}
}
time++;
}
// now check if all the oranges became rotten
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1)
// if there is still fresh orange, it was impossible
return -1;
}
}
return max(0, time);
}
};💡 Redundant Connection
In this problem, a tree is an undirected graph that is connected and has no cycles.
You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i]= [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.
Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.
Example 1:
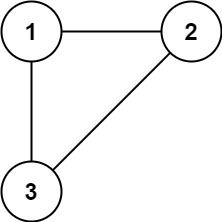
Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]Example 2:
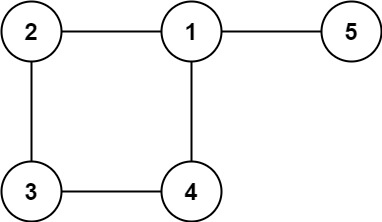
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
Output: [1,4]Solution
- 나의 첫번 approach는 ,, 너무 inefficient하다

-
그렇다면 degree를 기록해서 degree가 #nodes와 같아지는 순간의 edge를 return한다면?
1번보단 better time complexity이지만 여전히O(n^2)이다 -
O(n)해답을 알아보자
새로운 edge를 받을 때 마다 각 노드 두개중에 더 높은 rank를 가진 node한테 붙여주는거다
parent array의 각 index위치에는 그 노드의 parent노드 value를 보관한다
...
그냥 코드로 보자
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
vector<int> parent; //stores parent node # for each nodes
vector<int> rank; //stores the rank for each node
for (int i = 0; i <= n; i++) {
parent.push_back(i); //initially parent of a node is itself
rank.push_back(1); //initially rank of a node is 1
}
vector<int> result;
for (int i = 0; i < n; i++) {
int node1 = edges[i][0];
int node2 = edges[i][1];
if (!doUnion(node1, node2, parent, rank)) {
//doUnion fails
result = {node1, node2};
break;
}
}
return result;
}
private:
int doFind(int node, vector<int> &parent) {
int p = parent[node];
// the top parent will have itself as the parent
while (p != parent[p]) {
parent[p] = parent[parent[p]];
p = parent[p];
}
return p;
}
bool doUnion(int node1, int node2, vector<int> &parent, vector<int> &rank) {
// find parents for each node
int p1 = doFind(node1, parent);
int p2 = doFind(node2, parent);
if (p1 == p2) // already connected so this edge will cause cycle
return false;
// 더 rank가 높은 node에 지금 node를 attach
if (rank[p1] >= rank[p2]) {
rank[p1] += rank[p2];
parent[p2] = p1;
} else {
rank[p2] += rank[p1];
parent[p1] = p2;
}
return true;
}
};
