💡 Maximum Depth of Binary Tree

Given the root of a binary tree, return its maximum depth.

A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

Input: root = [1,null,2]
Output: 2

Solution

Recursion (DFS)

DFS: traversing depth first

재귀적으로 생각하면 간단하다

일단 현재 root가 null 포인터라면 length는 0
아니라면 leftchild 와 rightchild중에 더 깊은 depth를 가진애를 찾아서 +1을 해준다

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == NULL) return 0;
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};

Iteration (BFS)

BFS: traversing level by level

number of level = number of depth
그래서,, queue를 이용해서 그냥 level수를 세면 된다~!

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == NULL) {
            return 0;
        }
        queue<TreeNode*> q;
        q.push(root);
        int result = 0;
        while (!q.empty()) {
            int count = q.size();
            for (int i = 0; i < count; i++) {
                TreeNode* node = q.front();
                q.pop();
                if (node->left != NULL) {
                    q.push(node->left);
                }
                if (node->right != NULL) {
                    q.push(node->right);
                }
            }
            result++;
        }
        return result;
    }
};

💡 Minimum Depth of Binary Tree

위와 같은 문제이지만 이번엔 minimum depth 를 찾아보자

위의 코드를 조금만 바꾸면 되겠다

Solution

Recursion (DFS)

주의해야할 부분은 leafnode의 depth를 세지 않도록 하는 것 이다
leafnode에 minDepth를 돌린다면 0이 나오기 때문에 우리의 min 값이 영향을 받는다

자식이 하나만 있다면:
null이 아닌 자식에게만 recursion을 돌려야한다

(completely unbalanced tree를 생각해보자)

class Solution {
public:
    int minDepth(TreeNode* root) {
        if (root == NULL) return 0; //진짜 root만 여기 condition에 해당
        if (!root->left && !root->right) return 1; //leafnode

        // 자식이 존재한다는 경우에만 그자식에 대한 minDepth를 실행한다
        // 자식이 존재하지 않다면 depthend이기 때문에 우리의 min 계산에 영향을 주지 않도록 INT_MAX로 지정한다
        int left = root->left ? minDepth(root->left) : INT_MAX;
        int right = root->right ? minDepth(root->right) : INT_MAX;

        return min(left, right) + 1;
    }
};

Iterative (BFS)

핵심은: leafnode를 만나는 순간이 min depth이다!

class Solution {
public:
    int minDepth(TreeNode* root) {
        if (root == NULL) {
            return 0;
        }
        queue<TreeNode*> q;
        q.push(root);
        int result = 1;
        while (!q.empty()) {
            int count = q.size();
            for (int i = 0; i < count; i++) {
                TreeNode* node = q.front();
                q.pop();
                // if the node is a leafnode, min depth is here
                if (!node->left && !node->right) return result;
                // else push children into the queue and calculate the next level
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
            result++;
        }
        return result;
    }
};

💡 Merge Two Binary Trees

You are given two binary trees root1 and root2.

Imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not. You need to merge the two trees into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of the new tree.

Return the merged tree.

Note: The merging process must start from the root nodes of both trees.

Example 1:

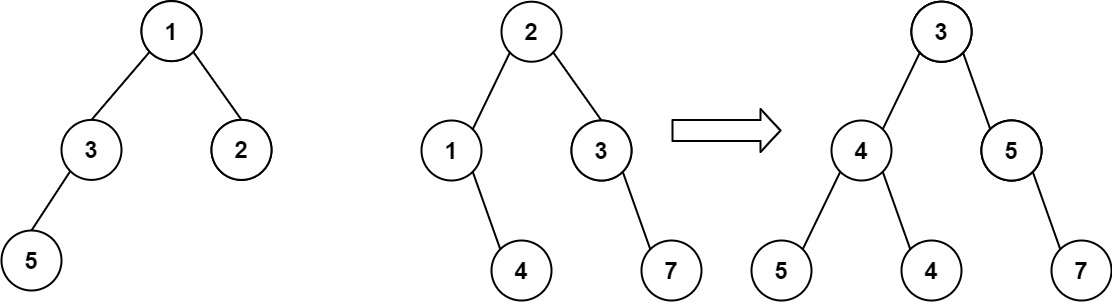
Input: root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
Output: [3,4,5,5,4,null,7]

Example 2:

Input: root1 = [1], root2 = [1,2]
Output: [2,2]

Solution

오 쉽네!
한번에 풀엇당

class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        TreeNode *merged; 

        if (root1 && root2) {
            // overlapping nodes
            int val = root1->val + root2->val;
            merged = new TreeNode(val);
            merged->left = mergeTrees(root1->left, root2->left);
            merged->right= mergeTrees(root1->right, root2->right);

        } else {
            // if not overlapping nodes
            if (root1) {
                merged = root1;
            } else {
                merged = root2;
            }
        }

        return merged;
    }
};

💡 Convert Sorted Array to Binary Search Tree

Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced binary search tree.

Example 1:

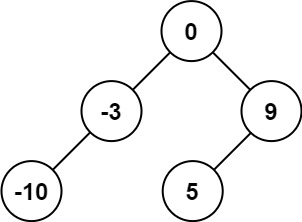
Input: nums = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: [0,-10,5,null,-3,null,9] is also accepted:

Example 2:

Input: nums = [1,3]
Output: [3,1]
Explanation: [1,null,3] and [3,1] are both height-balanced BSTs.

Solution

가운데를 나눠서 그 가운데를 기준으로 root라고 하고 양옆을 각각의 left, right children에게 준다!

아니 되게 간단한 문젠데 vector slicing 하는거 뭐 하는 것 마다 오류뜨냐 개빢치네

class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        if (nums.size() == 0) return NULL;

        int mid = nums.size() / 2 ;
        TreeNode *node = new TreeNode(nums[mid]);

        vector<int> left(nums.begin(), nums.begin() + mid);
        vector<int> right(nums.begin() + mid + 1, nums.end());

        node->left = sortedArrayToBST(left); 
        node->right = sortedArrayToBST(right); 

        return node;
    }
};

휴 드디어 됐네!!

💡 Path Sum

Given the root of a binary tree and an integer targetSum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals targetSum.

Example 1:

Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
Output: true
Explanation: The root-to-leaf path with the target sum is shown.

Example 2:

Input: root = [1,2,3], targetSum = 5
Output: false
Explanation: There two root-to-leaf paths in the tree:
(1 --> 2): The sum is 3.
(1 --> 3): The sum is 4.
There is no root-to-leaf path with sum = 5.

Example 3:

Input: root = [], targetSum = 0
Output: false
Explanation: Since the tree is empty, there are no root-to-leaf paths.

Solution

class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if (root == NULL) return false;

        int val = root->val;
        if (targetSum - val == 0 && !root->left && !root->right) return true;
        return hasPathSum(root->left, targetSum - val) || hasPathSum(root->right, targetSum - val);
    }
};

💡 Binary Tree Level Order Traversal

Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).

Example 1:

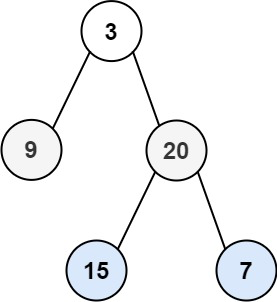
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]

Example 2:

Input: root = [1]
Output: [[1]]

Example 3:

Input: root = []
Output: []

Solution

output형태를 보면 ~ 이거는 딱봐도 recursion 아니고 iteration BFS네!

Queue를 쓰자!!

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;

        if (root == NULL) return result;

        queue<TreeNode*> q;
        q.push(root);

        while (!q.empty()) {
            vector<int> cur_level;
            int n = q.size();

            // for each level
            for (int i = 0; i < n; i++) {
                TreeNode *node = q.front();
                q.pop();

                cur_level.push_back(node->val);

                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }

            result.push_back(cur_level);
        }

        return result;
    }
};

💡 Binary Tree Zigzag Level Order Traversal

Given the root of a binary tree, return the zigzag level order traversal of its nodes' values. (i.e., from left to right, then right to left for the next level and alternate between).

Example 1:

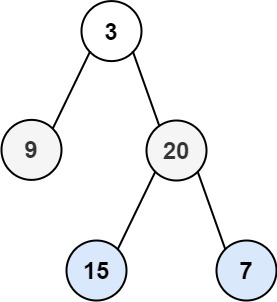
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[20,9],[15,7]]

Example 2:

Input: root = [1]
Output: [[1]]

Example 3:

Input: root = []
Output: []

Solution

바로 이전 문제를 갔다 써서 실제 답을 만들어 줄때 right → left 해줘야 하는 level에서는 숫자를 답 vector에서 앞에다가 삽입하는 방법으로 했다

class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        vector<vector<int>> result;

        if (root == NULL) return result;

        queue<TreeNode*> q;
        q.push(root);
        int level = 1;

        while (!q.empty()) {
            vector<int> cur_level;
            int n = q.size();

            // for each level
            for (int i = 0; i < n; i++) {
                TreeNode *node = q.front();
                q.pop();

                if (level % 2 == 0) {
                    // right->left 일때는 vector의 앞에다가 삽입해준다
                    cur_level.insert(cur_level.begin(), node->val);
                } else {
                    // left->right 일때는 순서대로 들어가도록 원래처럼 push 해준다
                    cur_level.push_back(node->val);
                }

                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }

            result.push_back(cur_level);
            level++;
        }

        return result;
    }
};

💡 Validate Binary Search Tree

Given the root of a binary tree, determine if it is a valid binary search tree (BST).

A valid BST is defined as follows:

The left subtree of a node contains only nodes with keys less than the node's key.
The right subtree of a node contains only nodes with keys greater than the node's key.
Both the left and right subtrees must also be binary search trees.

Example 1:

Input: root = [2,1,3]
Output: true

Example 2:

Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.

Solution

해당 subtree가 가질 수 있는 min값과 max값을 parameter에 유지해서 비교할 수 있게 한다

left child의 subtree의 값은 현재 root값 보다 커서는 안된다
right child의 subtree의 값은 현재 root값보다 작아서는 안된다

class Solution {
public:
    bool isValid(TreeNode* root, TreeNode* min, TreeNode* max) {
        if(root == NULL) return true;
        if(min && root->val <= min->val) return false;
        if(max && root->val >= max->val) return false;
        
        return isValid(root->left, min, root) && isValid(root->right, root, max);
    }
    
    bool isValidBST(TreeNode* root) {
        return isValid(root, NULL, NULL);
    }
};

💡 Construct Binary Tree from Preorder and Inorder Traversal

Given two integer arrays preorder and inorder, construct and return the binary tree.

Example 1:

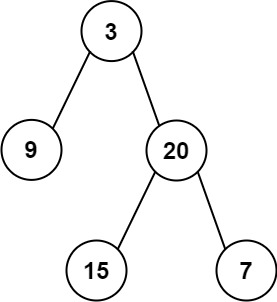
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

Example 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

Solution

preorder,, inorder,, 이거 뭔가 cs341인가에서 다 했던거 같은데 진짜 레알 기억 1도 안난다 ,, 미쳤

일단 이거라도 보면서 복기를 해보자,,,

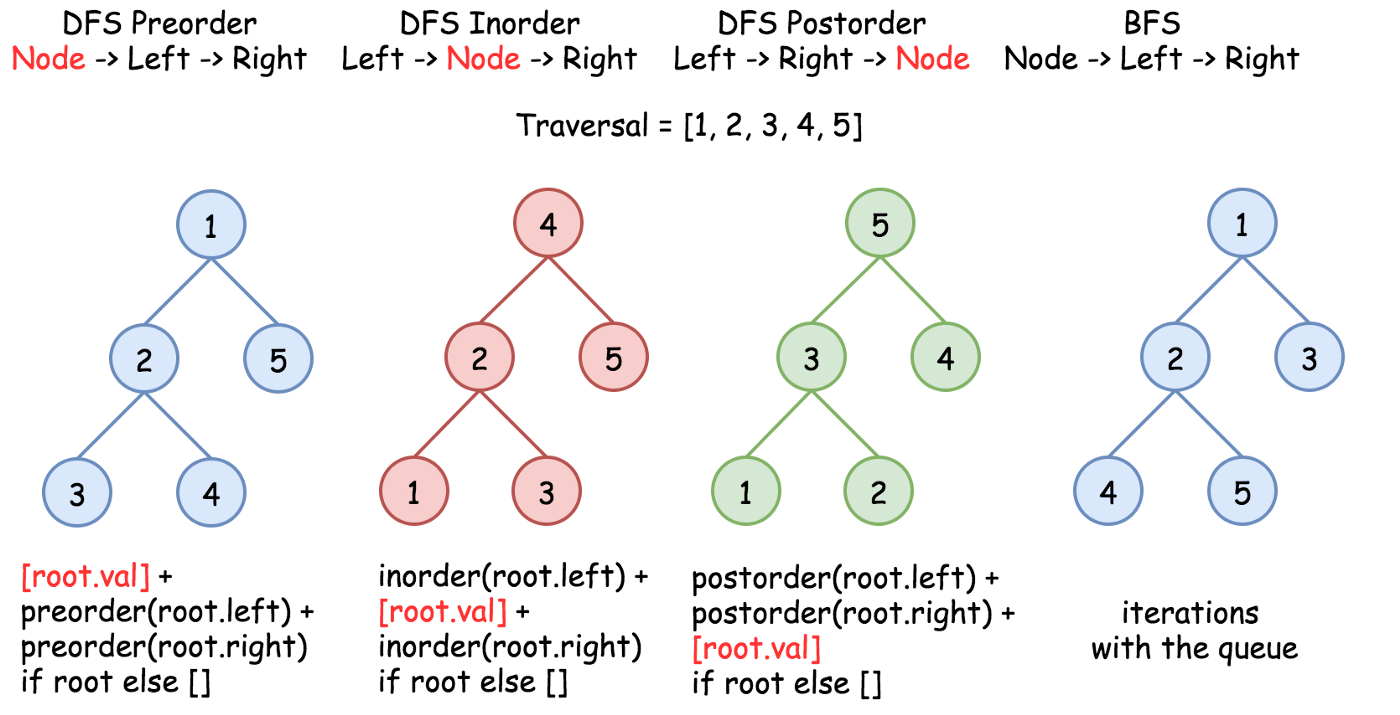
preorder traversal의 특징은:

• 제일먼저 root가 나오고
• 모든 left child를 먼저보고
• 그다음에 right child 를 보게 된다

위의 예시에서는 [1 2 3 4 5]가 될 것이다
‼️ 이 개념이 코드의 index에 적용된다

inorder traversal의 특징은:

root element를 찾으면 그 기준으로

• 왼쪽은 그 root의 left subtree이고
• 오른쪽은 right subtree이다

class Solution { 
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int index = 0;
        return build(preorder, inorder, index, 0, inorder.size() - 1);
    }
private:
    TreeNode* build(vector<int>& preorder, vector<int>& inorder, int& index, int i, int j) {
        // **
        // * 일단 index를 주소 값으로 받아 마치 global variable 인거처럼 사용하자
        // * *
        
		// i와 j는 inorder array의 index값이다 
        // 현재 node가 root가 되는 기준으로 봤을 때 inorder array[i:j+1]가 해당된다
        if (i > j) { // OOB
            return NULL;
        }
        
        TreeNode* root = new TreeNode(preorder[index]);
        
        int split = 0;
        for (int i = 0; i < inorder.size(); i++) {
            if (preorder[index] == inorder[i]) {
                split = i;
                break;
            }
        }

        // **
        // * preorder의 특징을 생각해보자
        // * 왼쪽애들 촤르륵 먼저하고 그담에 오른쪽애들이 시작된다
        // * 따라서 이 index를 생성된 function stack마다 한칸씩 올려주고
        // * index는 주소값을 받아와서 이전값이 유지가 되므로
        // * 이런방식이 통하는 것이다
        // ** 
        index++;
        // left build가 모두 끝나서야 right build가 시작된다
        // index를 이렇게 간편하게 줄 수 있는것은 preorder의 특징 덕분
        root->left = build(preorder, inorder, index, i, split - 1); 
        root->right = build(preorder, inorder, index, split + 1, j);
        
        return root;
    }
};

💡 Binary Tree Maximum Path Sum

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node's values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

Example 1:

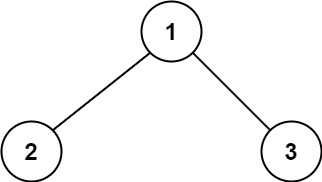
Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:

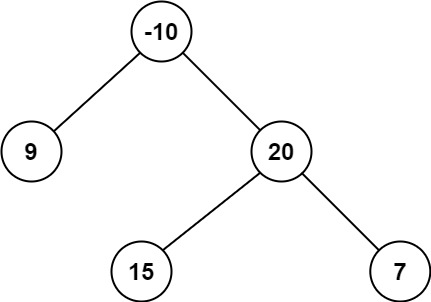
Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

Solution

이건 증맬루 어렵당 ,, 하지만 뭔가 인터뷰에 나올것 같은 질문이야,,

class Solution {
public:
    int maxPathSum(TreeNode* root) {
        int maxPath = INT_MIN;
        // maxPath is not updated when the path from root to leaf w/o split
        //  has the maxPath 
        // and the return value for this line will return such path
	    int m = dfs(root, maxPath); 
        return max(m, maxPath); 
    }
private:
    int dfs(TreeNode *root, int &maxPath) {
        if (root == NULL) return 0;

        // this will compute the subtrees
        //  will not consider split in the subtree
        //  left and right each represent the maxPath from bottom to root->left/root->right without any splits
        int left = max(dfs(root->left, maxPath), 0);
        int right = max(dfs(root->right, maxPath), 0);

        // we will eventually consider the split case in here
        int cur_path = root->val + left + right; 
        maxPath = max(cur_path, maxPath);

        // return "the maxPath from bottom to root without any splits"
        return root->val + max(left, right);
    }
};

---

💡 Implement Trie (Prefix Tree)

class TrieNode { // alphabet nodes
public:
    TrieNode* children[26];
    bool isWord; // to mark that this is a word
    
    TrieNode() {
        for (int i = 0; i < 26; i++) {
            children[i] = NULL;
        }
        isWord = false;
    }
};

class Trie { // this is the rootnode (wrapper)
private:
    TrieNode *root;

public:
    Trie() {
        root = new TrieNode();
    }
    
    void insert(string word) {
        // start from the root
        TrieNode *curr = root;
        int n = word.size();

        for (int i = 0; i < n; i++) {

            int idx = word[i] - 'a';
            
            if (curr->children[idx] == NULL) {
                // create new node when neccessary (wasn't created before)
                curr->children[idx] = new TrieNode();
            }
            curr = curr->children[idx];
        }
        
        // mark that this is a word
        curr->isWord = true;
    }
    
    bool search(string word) {

        TrieNode *curr = root;
        int n = word.size();

        for (int i = 0; i < n; i++) {

            int idx = word[i] - 'a';

            if (curr->children[idx] == NULL) {
                // when there isn't a word 
                return false;
            } 
            curr = curr->children[idx];
        }

        // if this is a word
        return curr->isWord;
    }
    
    bool startsWith(string prefix) {
        TrieNode *curr = root;
        int n = prefix.size();
        for (int i = 0; i < n; i++) {
            int idx = prefix[i] - 'a';
            if (curr->children[idx] == NULL) {
                return false;
            }
            curr = curr->children[idx];
        }
        // similar as search() but it doesn't have to be a word, 
        // just need to BE there without facing any NULL 
        return true;
    }
};

/**
 * Your Trie object will be instantiated and called as such:
 * Trie* obj = new Trie();
 * obj->insert(word);
 * bool param_2 = obj->search(word);
 * bool param_3 = obj->startsWith(prefix);
 */