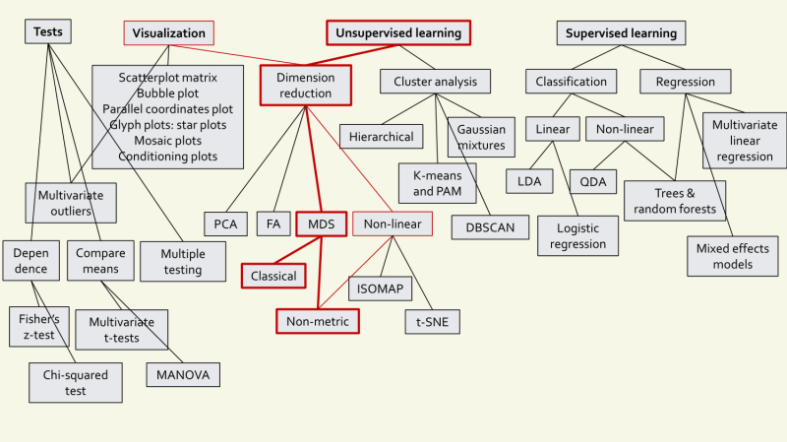
1. MDS(다차원 스케일링) 이란?
MDS는, 기본적으로 출력이 없는 입력 상태에서의 스케일 문제를 해결하는 것으로 Unsupervised Learning(비지도 학습) 범주에 들어간다. PCA로 차원 축소가 가능하지만, MDS를 사용해서도 차원 축소가 가능하다.
MDS 는 원 공간에서 모든 점들 간에 정의된 거리 행렬 D가 주어졌을 때, 임베딩 공간에서의 Euclidean distance 인 |yi − yj|와 거리 행렬 δi의 차이가 최소가 되는 임베딩 y를 학습한다. 학습 데이터가 원 공간의 벡터로 입력된다 하여도 x의 pairwise distance(관측값 쌍 간의 쌍별 거리) 를 계산함으로써 D를 만들 수 있다.
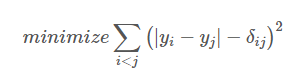
MDS 는 모든 점들 간의 거리 정보를 보존한다. 아래 사진에서는 지역 간의 거리 정보를 input 으로 이용하여 지역의 위치를 복원하는 예시를 보여준다. 그림의 좌측은 미국의 도시 간 거리이며, 우측은 이를 이용하여 MDS 를 학습한 결과이다. 거리 행렬이 2 차원 좌표 값으로부터 계산된 정보이기 때문에 2 차원 지도가 복원되었음을 알 수 있다. 단, y공간은 임의의 방향으로 회전될 수 있다.
낮은 차원에서의 자료들이 거리가 멀리 떨어져 위치한다는 것은 비유사성이 높다는 뜻이고, 자료가 가까울수록 비유사성이 낮다 (즉 유사성이 높다)는 뜻이 된다. MDS를 이용하여 데이터를 시각화 하는 방법의 가장 큰 장점은 바로 데이터들의 유사도를 확인할 수 있다는 점이다. (비슷한 변수값을 가지는 데이터들은 가까이 있다)
2. MDS와 PCA와의 차이점?
차원축소가 가능한 PCA와 비교하여 MDS의 차이점을 알아보면 아래와 같다.
| 주성분분석(PCA) | 다차원스케일링(MDS) | |
|---|---|---|
| 데이터 | d 차원 공간상에 있는 n 개의 인스턴스. {n×d 행렬로부터 시작 (X∈R^d)} | n 개의 인스턴스 간의 근접도(Proximity) 행렬. {n×n 행렬로부터 시작 (Dn×n)} |
| 목적 | 원 데이터 분산을 보존하는 기저의 부분집합 찾기 | 인스턴스의 거리 정보를 보존하는 좌표계 찾기 |
| 출력값 | 1) d 개의 고유벡터(eigenvectors) 2) d 개의 고윳값(eigenvalues) | d 차원에 있는 각 인스턴스의 좌표값 (X∈R^d) |
*MDS는 데이터 행렬 자체를 사용하지 않고, 관찰된 데이터들 사이의 거리를 사용한다.
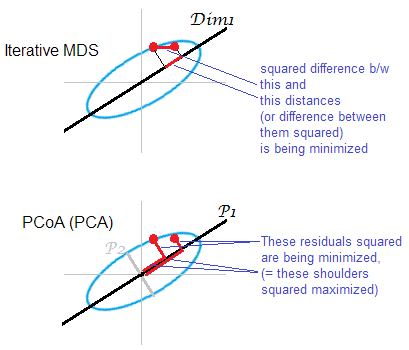
3. Metric MDS & Non-metric MDS?
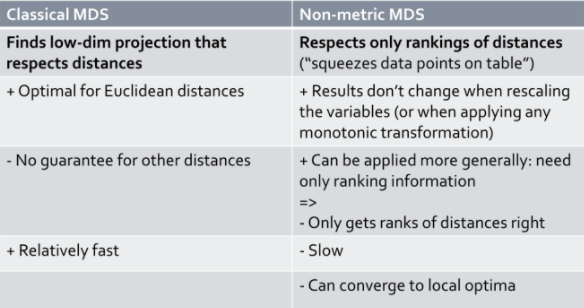
위 표는 Metric MDS와 Non-metric MDS를 비교한 것이다.
거리를 나타내는 (원 데이터의)거리를 유지하면서 낮은 차원으로의 투영을 찾는것이 Metric MDS의 목적이라면, Non-metric MDS에서는 거리의 랭킹을 유지하는 것이다.
Metric MDS의 장점으로는 유클리디안 거리에 최적화 되어 있다는 것이다. Non-metric MDS의 장점으로는 결과들이 다시 스케일링을 해도 바뀌지 않는다는 것이다. 또는 어떠한 단조적인 변환을 주더라도 결과가 바뀌지 않는다.
Metric MDS는 다른 거리에 대해서는 보장이 되지 않는다는 단점이 있다. 이에 비해 Non-metric은 더욱 일반적으로 적용이 가능하며, 오직 랭킹 정보만 필요하므로 오직 거리의 랭킹이 맞게 하는 데에 목적을 둔다.
또한 Metric MDS는 상대적으로 빠르며, Non-metric MDS는 다소 느리다는 차이가 있다.
4. MDS의 단점은?
MDS 는 모든 점들 간의 거리 정보의 중요도가 같다. 그렇기 때문에 가까운 점들 간의 거리 정보보다 멀리 떨어진 점들 간의 거리 정보의 영향력이 크다. 10 만큼 떨어진 점들 간의 거리가 5 틀리는 것과 1000 만큼 떨어진 점들 간의 거리가 5 만큼 틀리는 것의 중요도는 다르다. 하지만 MDS 는 이 두 거리차를 동일하게 중요하다고 판단한다. 그 결과 가까운 점들 간의 위치를 제대로 맞추는데 실패하게 된다. 고차원 공간에서의 거리는 가깝다라는 정보를 제외하면 대부분 차별성이 없는 무의미한 큰 값일 가능성이 높다. 하지만 MDS 는 무의미한 정보에 집중하여 고차원의 원 공간에서의 가까운 점들 간의 구조를 보존하지 못한다. 그리고 고차원 벡터를 저차원으로 임베딩할 때에는 특정 모양의 결과를 학습한다.
그러므로 MDS는 고차원 공간의 시각화에 적합한 방법이 아니다. 또한 MDS 는 metric space 를 가정한다. 고차원 공간이 metric space 가 아니라면, 즉 (a, b), (a, c) 가 가까우나 (b, c) 가 멀다면 MDS에서 설명되지 않는 공간이 되는 것이다.
아래와 같이 MDS는 고차원 공간에서는 자주 이러한 모습을 보인다. 고차원 공간에서는 대부분의 pairwise distances(관측값 쌍 간의 쌍별 거리)가 비슷한 값을 지닌다. 그리고 MDS 는 대부분의 정보가 무의미한 pairwise distances 정보를 보존하려 노력하다보니 이러한 모양으로 임베딩 공간을 학습하게 되는 것이다.
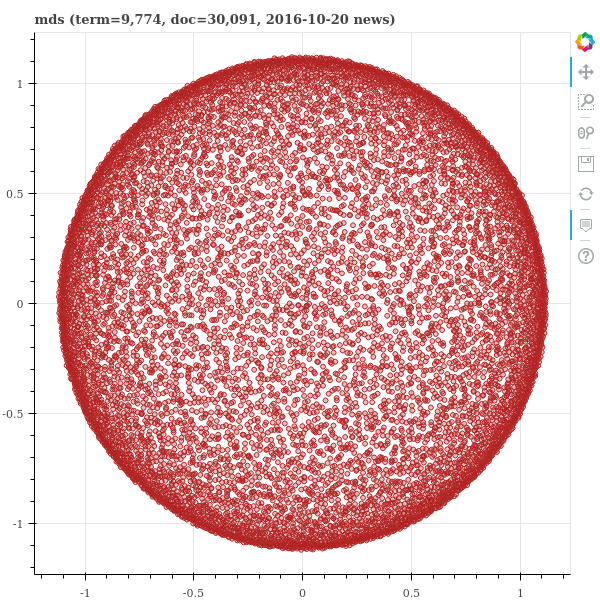
5. MDS의 분석 과정
-
자료수집
n개의 개체들을 대상으로 p개의 특성을 측정한다 -
유사성 / 비유사성 측정
mds 에서는 유사성이아니라 비유사성 측정방법을 사용함 ( 이유 - 유사성 대신에 비유사성(또는 거리)를 이용하는 이유는 유사성의 경우 대각선원소의 값을 정의하기 어렵기 때문이라고 함.) -
2차원, 3차원 공간상에 개체를 표현
개체들 사이의 유클리디안 거리(직선거리 계산방법) 를 비유사성 행렬을 이용해서 개체들을 2차원 공간상 점으로 표현한다.
**비유사성 행렬 = m개 객체로 구성된 데이터 세트의 경우, 데이터 세트에 m(m – 1)/2개 쌍이 있다. -
최적 표현의 결정
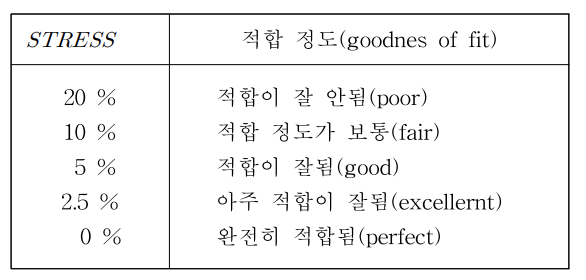
s-stress 를 사용해서 최적위치의 적합성을 측정한다.
오른쪽은 stress 구하는 방식 (dij 는 점i 부터 점 j 까지의 실제 유클리디안거리, ^dij는 프로그램에 의해서 추정된 거리)
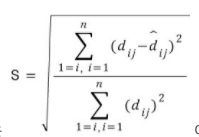
*유클리디안 거리계산법

출처 :
https://lovit.github.io/nlp/representation/2018/09/28/mds_isomap_lle/
https://peanut159357.tistory.com/51
https://blog.naver.com/PostView.nhn?blogId=sw4r&logNo=221034787271&parentCategoryNo=&categoryNo=157&viewDate=&isShowPopularPosts=false&from=postView