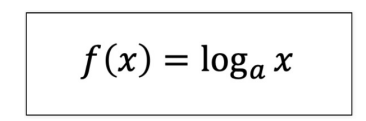모델평가
어떤 모델이 좋다고 말할 수 있을까?
예를들어, 회귀모델들은 실제값과 예측값의 차이를 가지고 계산해서 그 에러가 최소가 되게 하는 모델을 선택한다.
하지만 분류 모델은 정확도(accuracy), 오차행렬(confusion matrix), 정밀도(precision), 재현율(recall), f1-score 등 평가 항목이 조금 많다.
이들에 대해 한 번 살펴보자.
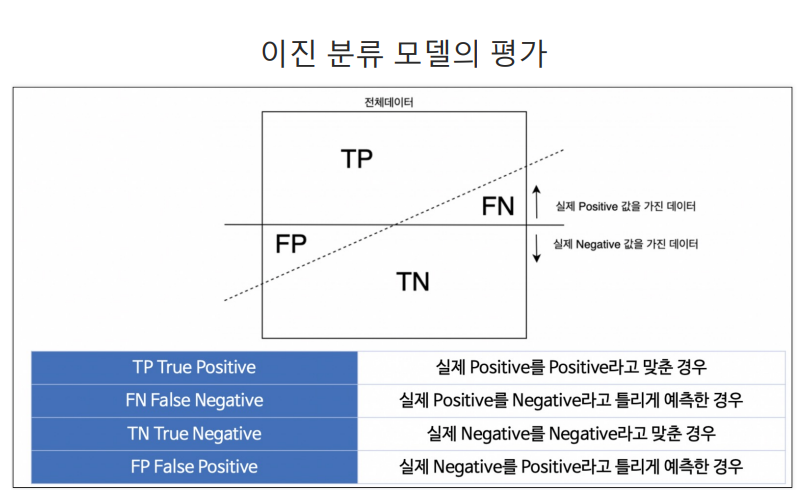
이진분류 (0,1) -> 와인데이터에서의 화이트0 와인 1 같은
예측의 결과에 따라 4가지로 구분할 수 있다.
- TP : 실제 1인데 1(Positive)이라고 맞춘경우(True)
- FN : 실제 1인데 0(Negative)이라고 틀린경우(False)
- TN : 실제 0인데 0(Negative)이라고 맞춘경우(True)
- FP : 실제 0인데 1(Positive)이라고 틀린경우(False)
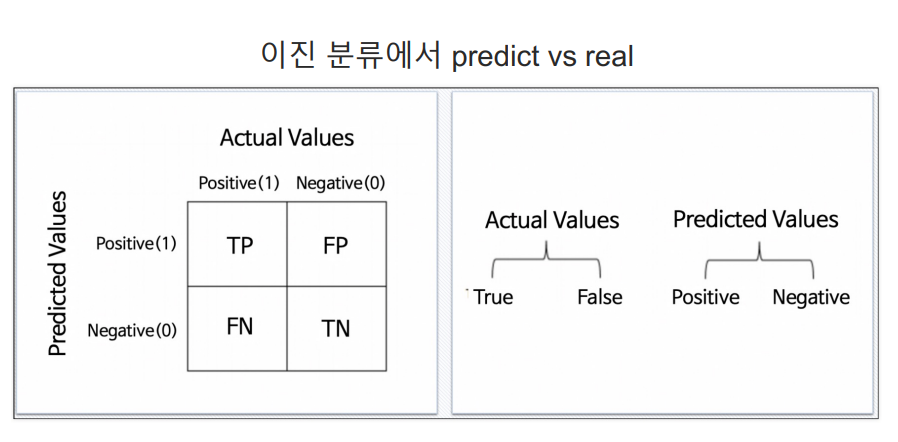
좀 쉽게 이해하자면 실제값을 True/False로 예측값을 Positive/Negative라고 분류한다.
- 정확도(Accuracy)
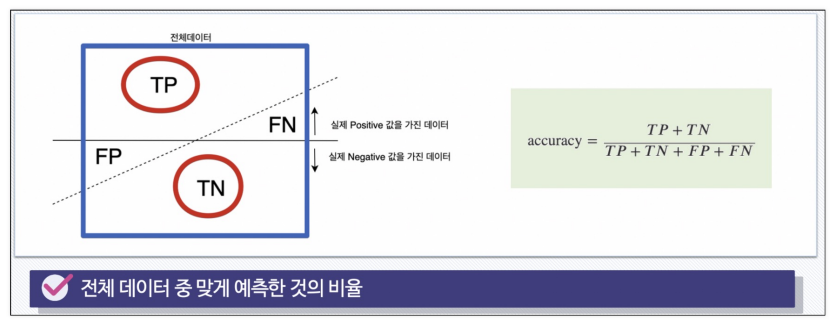
📢 전체 중에 실제로 맞춘 값의 비율로 익히 많이 사용해왔었다.
(맞춘값/전체)
- 정밀도(Precision)

📢 1(positive)이라고 예측한 것중 실제로 1(positive)이였던 값의 비율이다.
(모델이 1이라고 한것중에 진짜 1의 비율)
Precision이 자주 사용되는 예는 <스팸 메일>이다.
스펨 메일이 많이 쌓여있는 것은 문제가 안된다.
하지만 스팸 메일이라고 분류한 것들 중에 중요한 메일이 섞여 들어가있다면 문제가 된다.
이처럼 positive라고 예측한 것중 실제로 positive라고 예측하는 것이 중요한 분석에서는 Precision을 많이 사용한다.
- 재현율(Recall)

📢 실제로 1(positive)인 데이터들 중 1(positive)이라고 예측한 데이터의 비율이다.
Recall은 놓쳐서는 안되는 일을 체크해야될 때 자주 사용된다.
예를 들어 환자들이 암 검사를 받으러 왔는데
암 환자가 아닌 사람들을 암이라고 진단하는 것은 다시 검사해서 아니라고 하면 되지만,
암 환자인 사람들을 암이 아니다라고 진단하는 것은 문제를 일으킬 수 있다.
이처럼 실제로 참(True)인 데이터들 중 참(True)이라고 예측하는 것이 중요한 분석에는 Recall이 모델의 성능을 평가하는 중요한 지표가 될 것이다.
(놓쳐서는 안되는 1을 예측해야할 때)
- Fall-Out
📢 실제로 1(positive)가 아닌데, 1(positive)이라고 예측한 값의 비율이다.
threshold
지금까지 분류 모델을 적용한 분류기들은 해당 클래스에 속할 확률을 반환하여 어떤 클래스에 속하는지 분류했다.
예를 들어 iris 데이터의 경우 가장 높은 확률값이 있는 클래스를 해당 값이라고 하고
타이타닉 데이터에서는 0.5를 기준으로 그 결과보다 높으면 살아남고(1), 낮으면 살아남지 못한다(0)고 분류했다.
여기에서 기준이 되는 0.5 와 같은 값을 threshold라 한다.
그렇다면 threshold에 따라서 각 모델 평가 지표의 값들도 달라질 수 있지 않을까? 란 생각을 하게 된다. 한 번 살펴보자.
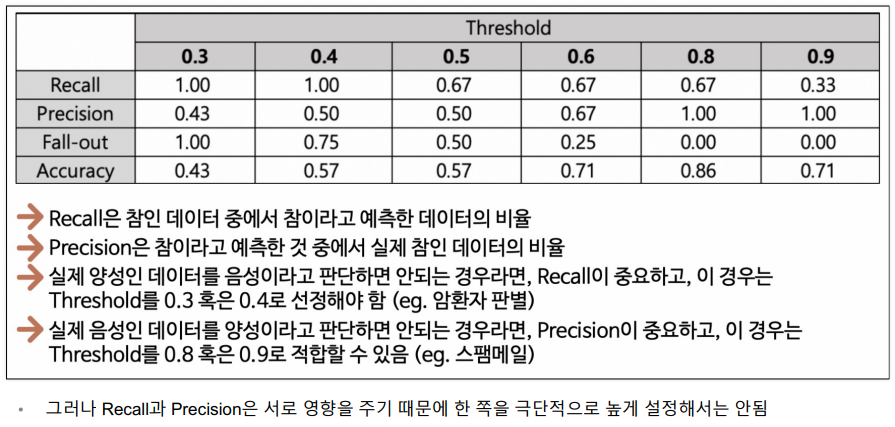
여기에서 알 수 있는 것은 threshold가 0.5인 것이 무조건 좋다!라고 판단할 수 있는건 아니라는 사실이다.
게다가 각 지표들(특히, Recall과 Precision)은 서로 영향을 받으므로 한 지표만 보고 극단적으로 threshold를 높이거나 낮추는 것도 좋은 방법은 아니다.
그렇다면 Recall과 Precision을 한 번에 확인할 수 있는 지표는 없을까?
F1-Score

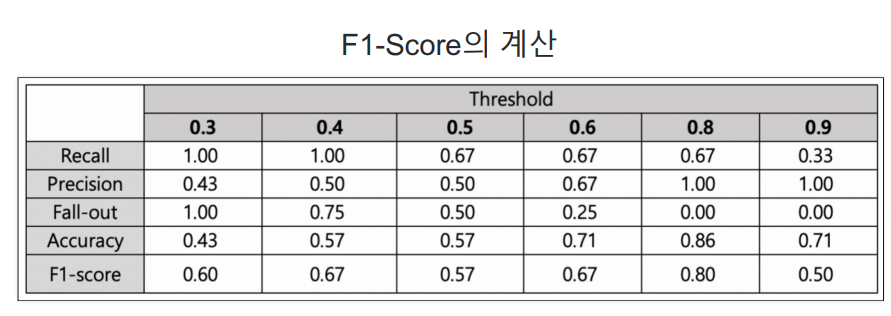
f1-score를 사용하면 recall과 precision이 어느 한 쪽으로 치우치지 않고 둘 다 높은 값을 가질수록 높은 값을 가지는 지표로 사용되므로 자주 사용되는 지표 중 하나이다.
ROC 곡선
FPR(False Positive Rate : fallout)이 변할 때 TPR(True Positive Rate : Recall)의 변화를 그린 그림으로 FPR이 x축, TRP이 y축에 위치
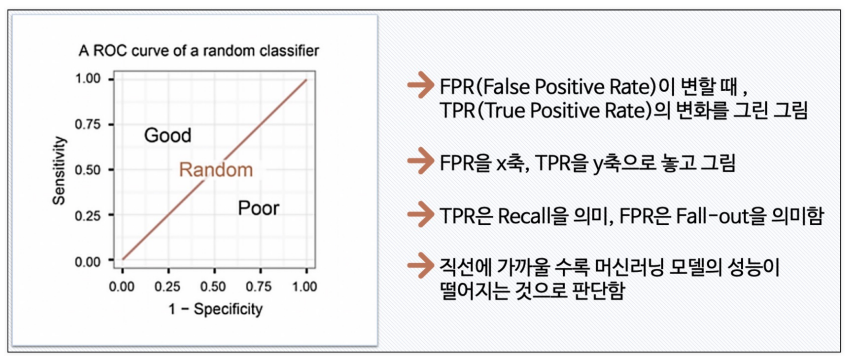
ROC 곡선이 직선에 가까울수록 머신러닝 모델의 성능이 떨어지는 것으로 판단하고 위로 볼록한 그래프가 그려질수록 잘 구분하고 있는 모델이다라고 생각할 수 있다.
AUC
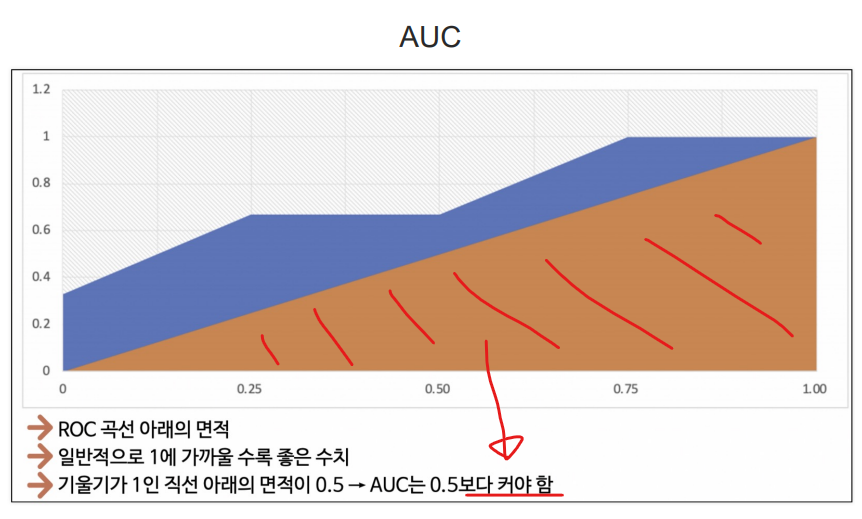
이때 ROC 곡선 아래의 면적을 AUC 라고 하는데
ROC가 위로 볼록할수록 좋은 모델이라고 했으니, AUC가 1에 가까울수록 좋은 모델이다라고 할 수 있다.
또한 ROC 곡선이 직선이면 모델의 성능이 떨어지는 것이므로 AUC가 0.5 보다는 커야 유의미한 결과를 내는 모델이라고 판단할 수 있다.
와인 데이터를 이용한 각 모델 평가 수치
- 데이터 준비
# ----데이터 읽기
# 1) 데이터 불러오기 & concat
import pandas as pd
red_url = 'https://raw.githubusercontent.com/PinkWink/ML_tutorial/master/dataset/winequality-red.csv'
white_url = 'https://raw.githubusercontent.com/PinkWink/ML_tutorial/master/dataset/winequality-white.csv'
red_wine = pd.read_csv(red_url, sep=';')
white_wine = pd.read_csv(white_url, sep=';')
red_wine['color'] = 1.
white_wine['color'] = 0.
wine = pd.concat([red_wine, white_wine])
# 2) 맛 분류를 위한 데이터 정리
wine['taste'] = [1. if grade > 5 else 0 for grade in wine['quality']]
X = wine.drop(['taste','quality'], axis= 1) # 데이터
y = wine['taste'] # 맛 라벨
# ----결정나무 적용
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
# 4)훈련, 학습데이터분리
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2, random_state=42)
# 5)훈련
wine_tree = DecisionTreeClassifier(max_depth=2, random_state=42)
wine_tree.fit(X_train, y_train)
# 6)예측
y_pred_tr = wine_tree.predict(X_train)
y_pred_test = wine_tree.predict(X_test)
# 7)정확도
print('Train ACC : ', accuracy_score(y_train, y_pred_tr))
print('Test ACC : ', accuracy_score(y_test, y_pred_test))
Train ACC : 0.7383105637868
Test ACC : 0.7084615384615385
- 수치 구해보기
# 각 수치 구해보기
from sklearn.metrics import(accuracy_score, precision_score, recall_score, f1_score, roc_auc_score, roc_curve)
print('Accuracy : ', accuracy_score(y_test, y_pred_test))
print('Recall : ', recall_score(y_test, y_pred_test))
print('Precision : ', precision_score(y_test, y_pred_test))
print('AUC : ', roc_auc_score(y_test, y_pred_test))
print('F1 Score : ', f1_score(y_test, y_pred_test))Accuracy : 0.7084615384615385
Recall : 0.8150765606595995
Precision : 0.7571115973741794
AUC : 0.6614185464051878
F1 Score : 0.7850255246738514
- ROC커브그리기
import matplotlib.pyplot as plt
pred_proba = wine_tree.predict_proba(X_test)[:,1] #1일 확률만 뽑아보기
fpr, tpr, thresholds = roc_curve(y_test,pred_proba )
plt.figure(figsize=(10,8))
plt.plot([0,1],[0,1]) # 직선
plt.plot(fpr, tpr)
plt.grid()
plt.show()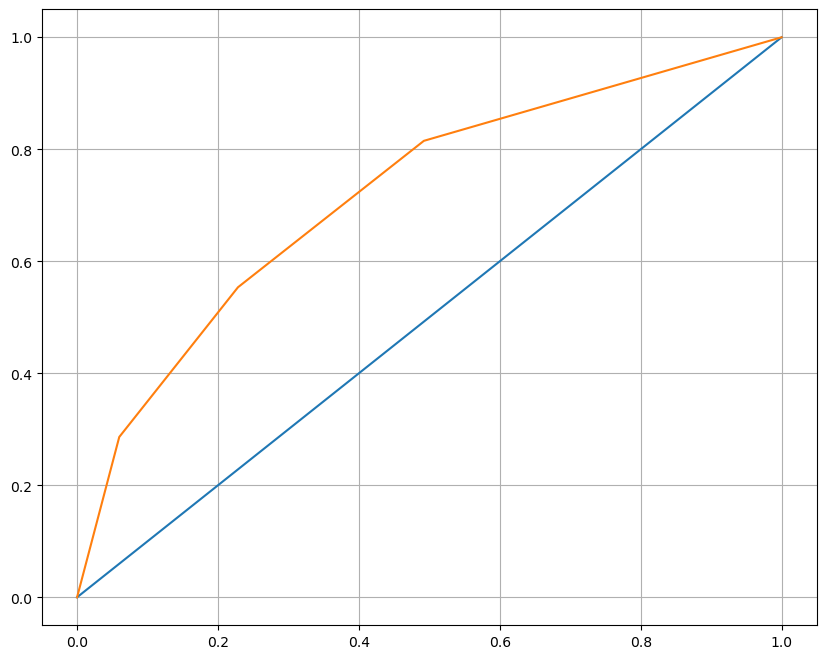
수학의기초
(1) 다항함수
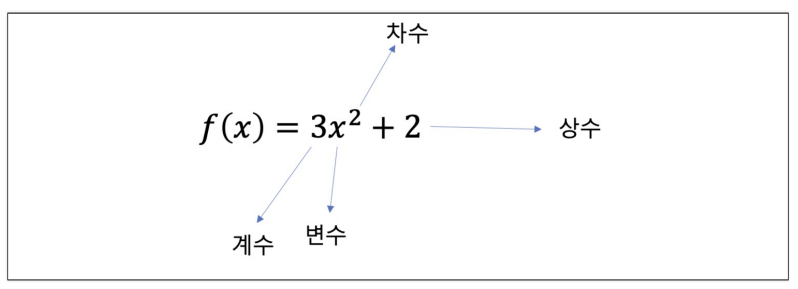
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3,2,100) # -3부터 2까지 100등분
y = 3*x**2 + 2plt.figure(figsize=(12,8))
plt.plot(x,y)
plt.grid()
plt.xlabel('$x$',fontsize = 25)
plt.ylabel('$y$',fontsize = 25)
plt.show()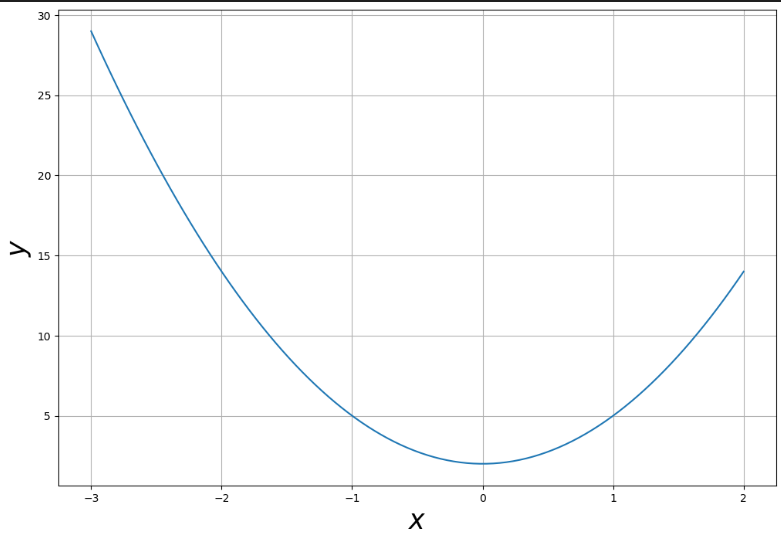
- 다항함수의 x 축 방향 이동
x = np.linspace(-5,5,100)
y1 = 3*x**2 + 2
y2 = 3*(x+1)**2 + 2plt.figure(figsize=(12,8))
plt.plot(x,y1, ls = 'dashed', label = '$y=3x^2+2$')
plt.plot(x,y2, label = '$y=3(x+1)^2+2$')
plt.legend(fontsize = 15) #라벨노출
plt.grid()
plt.xlabel('$x$',fontsize = 25)
plt.ylabel('$y$',fontsize = 25)
plt.show()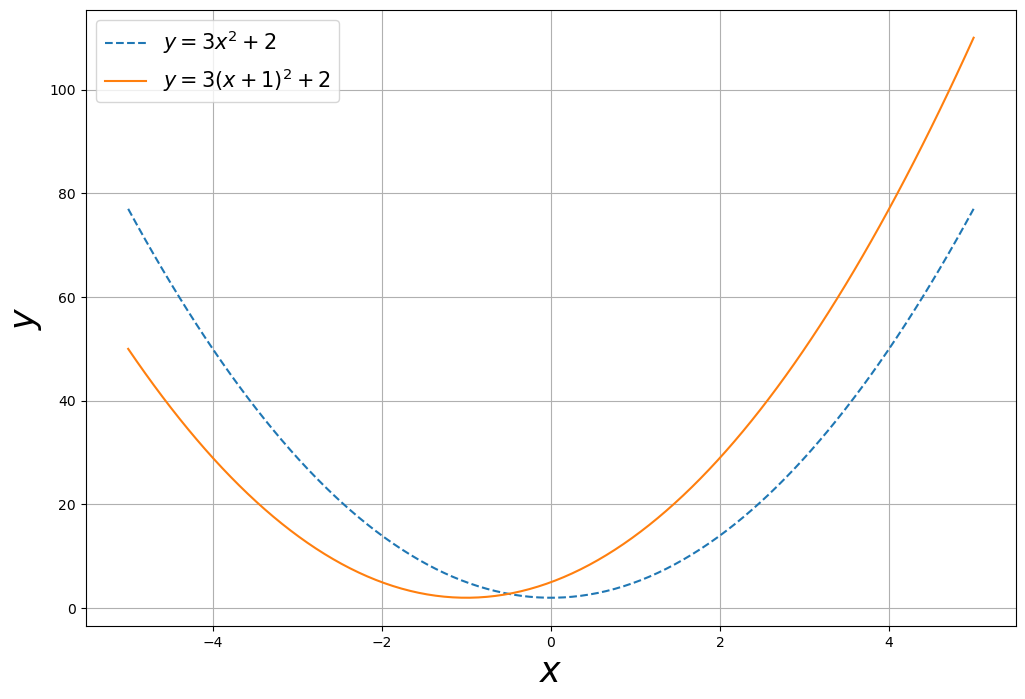
(2) 지수함수
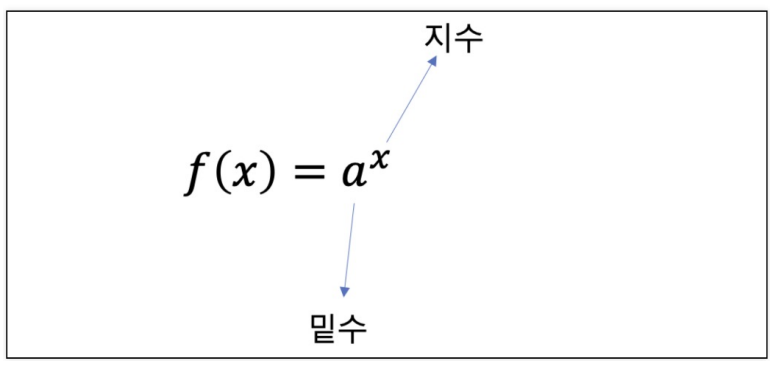
x = np.linspace(-2,2,100)
a11 , a12, a13 = 2,3,4
y11, y12, y13 = a11**x, a12**x, a13**x
a21,a22,a23 = 1/2,1/3,1/4
y21,y22,y23 = a21**x, a22**x, a23**xfig, ax = plt.subplots(1,2,figsize = (12,6))
ax[0].plot(x,y11,color='k', label = "$2^x$")
ax[0].plot(x,y12,'--',color='k', label = "$3^x$")
ax[0].plot(x,y13,':',color='k', label = "$4^x$")
ax[0].legend(fontsize = 18)
ax[1].plot(x,y21,color='k', label = "$(1/2)^x$")
ax[1].plot(x,y22,'--',color='k', label = "$(1/3)^x$")
ax[1].plot(x,y23,':',color='k', label = "$(1/4)^x$")
ax[1].legend(fontsize = 18)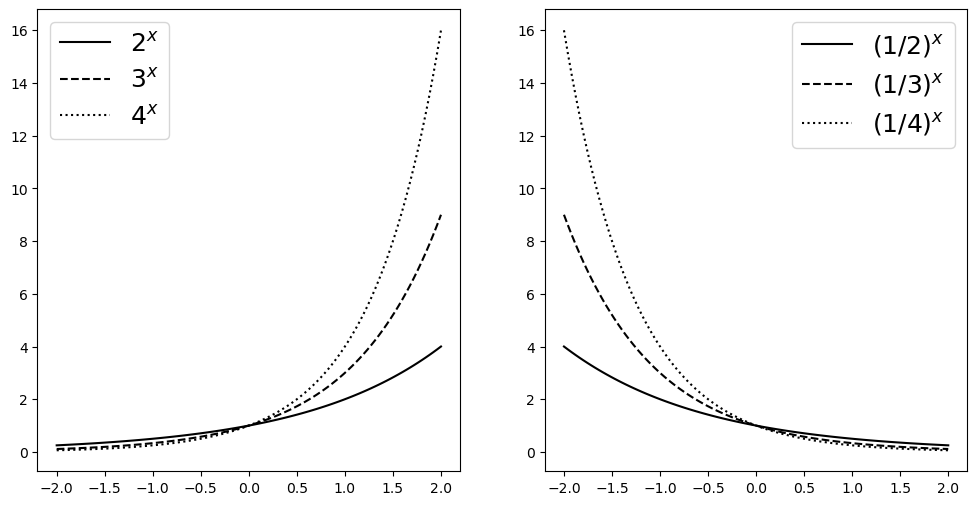
- 지수증가
x = np.linspace(0,10)
plt.figure(figsize=(6,6))
plt.plot(x, x**2, '--', color = 'k', label = '$x^2$')
plt.plot(x, 2**x, color = 'k', label = '$2^x$')
plt.legend(loc='center left', fontsize = 25)
plt.xlabel('$x$', fontsize = 25)
plt.ylabel('$y$', fontsize = 25)
plt.show()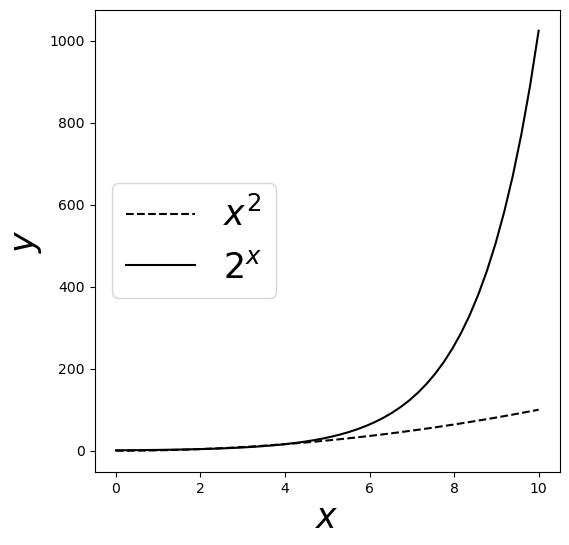
(3) 로그함수