💡그래프 알고리즘이란,
그래프와 같은 복잡하고 연결성이 높은 자료구조에서
순회 (Graph Traversal), 탐색 및 검색 (Graph Search) 등과 같은 목적으로 사용되는 알고리즘이다.
신장 트리 Spanning Tree
💡신장 트리란,
그래프 내의 모든 정점을 포함하는 트리로, 최소의 간선으로 모든 정점이 연결되어 있는 순환성이 없는 부분 그래프이다.

신장 트리는 최소의 간선 V-1개의 간선으로 구성되기 때문에 하나의 그래프에 여러 개의 신장 트리가 존재할 수 있다.
💡최소 신장 트리 알고리즘이란,
최소 신장 트리란 그래프 내의 여러 신장 트리 중 가중치가 최소가 되는 신장 트리를 말하며, 최소 신장 트리 알고리즘은 그래프 내의 최소 신장 트리를 찾는 알고리즘이다.
최소 신장 트리 알고리즘에는 2가지 알고리즘이 대표적이다.
🔘 크루스칼 알고리즘 Kruskal Algorithm
🔘 프림 알고리즘 Prim Algorithm
크루스칼 알고리즘 Kruskal Algorithm
💡알고리즘 원리💡
그래프에서 간선을 하나씩 추가하면 최소 신장 트리를 만드는 방식의 알고리즘이다. 간선을 추가할 때는 그리디 알고리즘을 사용하여 선택 당시 가중치가 최소인 간선을 선택한다.
🔗동작 과정
- 간선을 가중치를 기준으로 오름차순 정렬한다.
- 간선을 순차적으로 순회하면서 최소 신장 트리를 만든다.
이때, 서로소 집합 알고리즘에 기반하여 트리에 순환성이 생기지 않는 간선만 추가한다. - 최소 신장 트리가 될 때까지 2번 과정을 반복한다.
👀예제와 함께 살펴보기
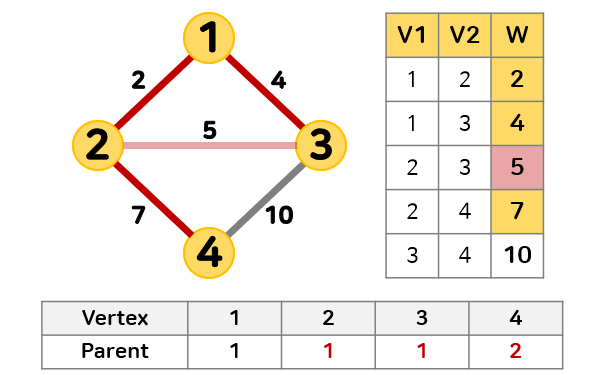
다음과 같은 그래프가 있을 때 최소 신장 트리를 찾고자 한다.

- 가중치를 기준으로 간선을 오름차순 정렬한다.
선택 과정에서 가중치가 최소인 간선을 추가하며 최소 신장 트리를 만들기 때문에 간선을 오름차순 정렬해야 한다.
최소 신장 트리의 순환성을 확인하기 위해 부모 정점을 기록한다.
초기 부모 정점은 자기 자신이 되며 간선이 추가될 때마다 갱신된다.

- 순회하지 않은 간선 중 가중치가 2로 가장 작은 간선 를 선택한다.
정점 1과 정점 2의 부모 정점이 다르기 때문에 순환성이 생기지 않아 간선 를 추가할 수 있다.
추가된 간선에 의해 정점 2의 부모 정점은 정점 1로 갱신된다.

- 순회하지 않은 간선 중 가중치가 4로 가장 작은 간선 을 선택한다.
정점 1과 정점 3의 부모 정점이 다르기 때문에 순환성이 생기지 않아 간선 을 추가할 수 있다.
추가된 간선에 의해 정점 3의 부모 정점은 정점 1로 갱신된다.

- 순회하지 않은 간선 중 가중치가 5로 가장 작은 간선 을 선택한다.
정점 2과 정점 3의 부모 정점이 같기 때문에 순환성이 생기므로 간선 을 추가할 수 없다.

- 순회하지 않은 간선 중 가중치가 7로 가장 작은 간선 를 선택한다.
정점 2과 정점 4의 부모 정점이 다르기 때문에 순환성이 생기지 않아 간선 를 추가할 수 있다.

따라서 주어진 그래프에서 최소 신장 트리는 가중치 합이 13인 부분 그래프가 된다.
🔎알고리즘 특징🔎
🔘 크루스칼 알고리즘에서는 순환성을 확인하기 위해 서로소 집합 알고리즘을 활용한다. 최소 신장 트리란 최소한의 간선의 수로 연결된 순환성이 없는 부분 그래프이다.
🔘 크루스칼 알고리즘에서는 그리디 알고리즘을 사용하여 선택 당시 가중치 값이 최소인 간선을 선택하기 때문에 간선을 가중치를 기준으로 오름차순 정렬해야 한다.
⏰시간 복잡도
시간 복잡도란,
문제를 해결하는데 걸리는 시간과 입력의 함수 관계를 나타내는 지표로,
주로 계수와 낮은 차수의 항을 제외시키는 빅-오 표기법을 사용한다.
크루스칼 알고리즘에서는 정렬, 간선 순회, 서로소 집합 연산이 있다. 간선 순회는 간선의 개수 만큼 시간이 걸리며, 서로소 집합 연산은 통상적으로 로 계산한다. 간선을 정렬하는 데 걸리는 시간이 지배적이기 때문에 시간 복잡도가 이다.
| 알고리즘 | 정렬 | 간선 순회 | 서로소 집합 |
|---|---|---|---|
| 크루스칼 알고리즘 |
💻코드 구현💻
# 그래프 클래스
class Graph:
# 변수 정리
def __init__(self, v):
self.v = v #정점 수
self.edge = [] #간선 리스트
self.parent = list(range(v+1)) #부모 정점 기록
# 간선 추가
def add(self, a, b, w):
self.edge.append((w, a, b))
# 정점이 속한 집합 찾기
def find(self, v):
if self.parent[v] == v:
return v
self.parent[v] = self.find(self.parent[v])
return self.parent[v]
# 두 정점이 속한 집합 합치기
def union(self, a, b):
p1 = self.find(a)
p2 = self.find(b)
if p1 < p2:
self.parent[p2] = p1
else:
self.parent[p1] = p2
# 크루스칼 알고리즘
def kruskal(self):
result = 0
self.edge.sort() # 간선 오름차순 정렬
for w, a, b in self.edge:
if self.find(a) != self.find(b): # 순환성이 없는 경우
self.union(a, b) # 부모 정점 갱신
result += w # 간선 추가
return result# 예제
g = Graph(4)
g.add(1,2,2)
g.add(1,3,4)
g.add(2,3,5)
g.add(2,4,7)
g.add(3,4,10)
print(*g.edge)
g.kruskal()
# (2, 1, 2) (4, 1, 3) (5, 2, 3) (7, 2, 4) (10, 3, 4)
# 13