💡그래프 알고리즘이란,
그래프와 같은 복잡하고 연결성이 높은 자료구조에서
순회 (Graph Traversal), 탐색 및 검색 (Graph Search) 등과 같은 목적으로 사용되는 알고리즘이다.
신장 트리 Spanning Tree
💡신장 트리란,
그래프 내의 모든 정점을 포함하는 트리로, 최소의 간선으로 모든 정점이 연결되어 있는 순환성이 없는 부분 그래프이다.

신장 트리는 최소의 간선 V-1개의 간선으로 구성되기 때문에 하나의 그래프에 여러 개의 신장 트리가 존재할 수 있다.
💡최소 신장 트리 알고리즘이란,
최소 신장 트리란 그래프 내의 여러 신장 트리 중 가중치가 최소가 되는 신장 트리를 말하며, 최소 신장 트리 알고리즘은 그래프 내의 최소 신장 트리를 찾는 알고리즘이다.
최소 신장 트리 알고리즘에는 2가지 알고리즘이 대표적이다.
🔘 크루스칼 알고리즘 Kruskal Algorithm
🔘 프림 알고리즘 Prim Algorithm
프림 알고리즘 Prim Algorithm
💡알고리즘 원리💡
그래프에서 정점을 하나씩 추가하면 최소 신장 트리를 만드는 방식의 알고리즘이다. 정점을 추가할 때는 그리디 알고리즘을 사용하여 선택 당시 정점과 연결된 간선의 가중치가 최소인 정점을 선택한다.
🔗동작 과정
- 임의의 정점을 시작 정점으로 선택하여 최소 신장 트리를 만든다.
- 삽입된 정점과 인접한 정점 중 연결된 간선의 가중치가 가장 작은 정점을 최소 신장 트리에 추가한다.
이때, 서로소 집합 알고리즘에 기반하여 트리에 순환성이 생기지 않는 정점만 추가한다. - 최소 신장 트리가 될 때까지 2번 과정을 반복한다.
👀예제와 함께 살펴보기
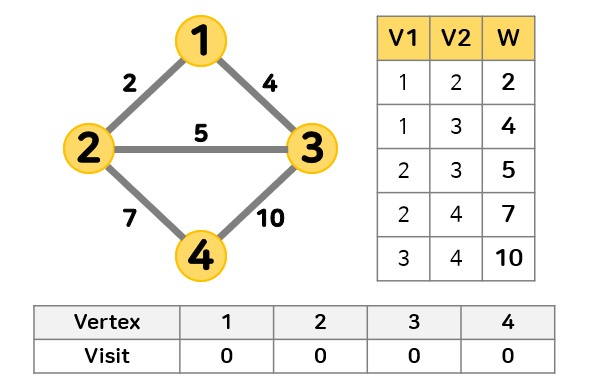
다음과 같은 그래프가 있을 때 최소 신장 트리를 찾고자 한다.

- 빈 최소 신장 트리를 만든다.
정점을 추가하며 최소 신장 트리를 만들기 때문에 순환성 확인 및 반복 방지를 위해 각 정점을 방문했는지 기록한다.
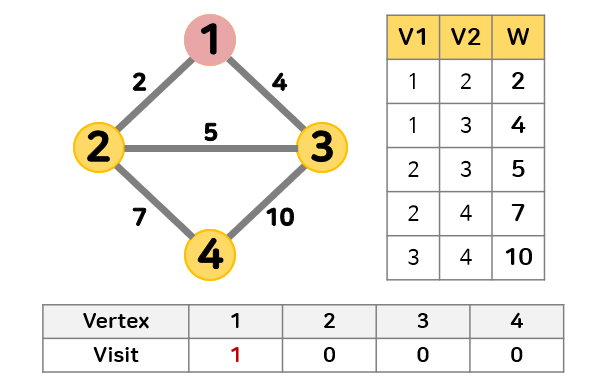
- 방문하지 않은 정점 중 임의의 정점 1을 선택해 최소 신장 트리에 추가한다.
최소 신장 트리에 추가했기 때문에 정점 1의 방문을 1로 갱신한다.
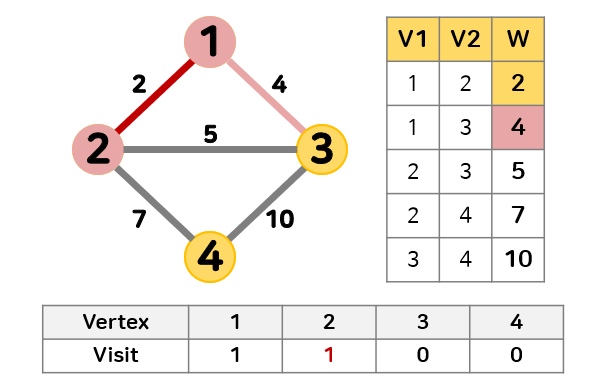
- 최소 신장 트리에 있는 정점 1과 인접한 정점 중 간선의 가중치가 2로 가장 작은 정점 2를 최소 신장 트리에 추가한다.
정점 2의 방문 기록이 0이기 때문에 순환성이 없어 추가할 수 있다.
최소 신장 트리에 추가했기 때문에 정점 2의 방문을 1로 갱신한다.
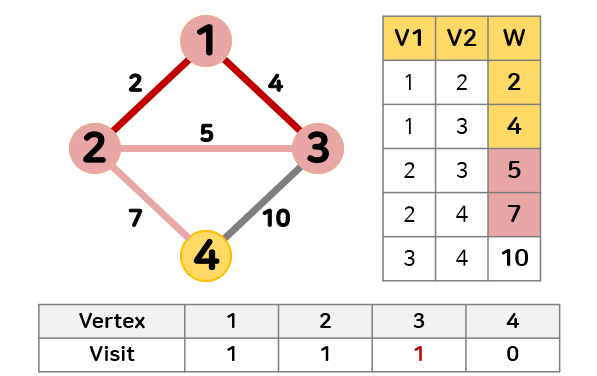
- 최소 신장 트리에 있는 정점 1, 2와 인접한 정점 중 간선의 가중치가 4로 가장 작은 정점 3를 최소 신장 트리에 추가한다.
정점 3의 방문 기록이 0이기 때문에 순환성이 없어 추가할 수 있다.
최소 신장 트리에 추가했기 때문에 정점 3의 방문을 1로 갱신한다.
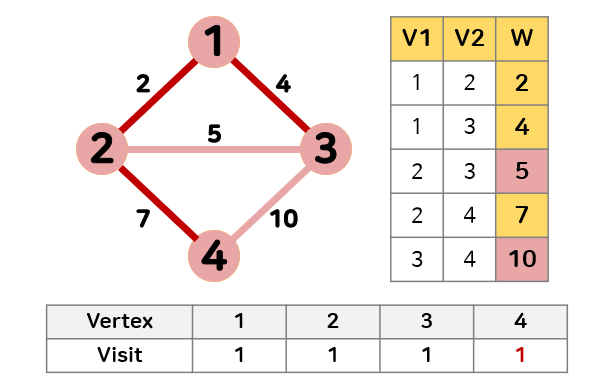
- 최소 신장 트리에 있는 정점 1, 2, 3과 인접하며 방문하지 않은 정점 중 간선의 가중치가 7로 가장 작은 정점 4를 최소 신장 트리에 추가한다.
간선의 가중치는 5가 가장 작지만 2와 3의 방문 기록은 1로 추가할 경우 순환성이 생기기 때문에 추가할 수 없다.
정점 4의 방문 기록은 0이기 때문에 순환성이 없어 추가할 수 있다.
최소 신장 트리에 추가했기 때문에 정점 4의 방문을 1로 갱신한다.
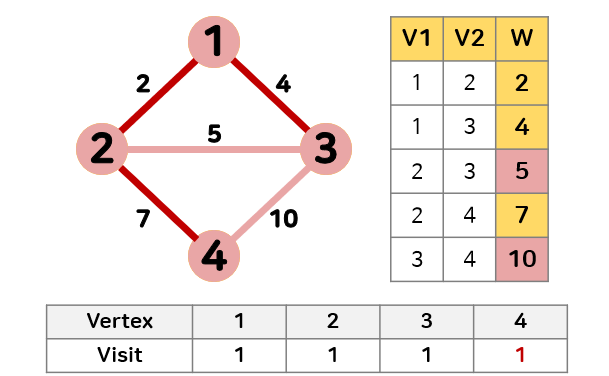
따라서 주어진 그래프에서 최소 신장 트리는 가중치 합이 13인 부분 그래프가 된다.
🔎알고리즘 특징🔎
🔘 프림 알고리즘에서는 그리디 알고리즘을 사용하여 선택 당시 간선의 가중치 값이 최소인 정점을 선택하기 때문에 정점과 연결된 간선을 가중치를 기준으로 오름차순 정렬해야 한다.
매번 정렬이 필요하기 때문에 우선순위 큐를 사용하기도 한다.
⏰시간 복잡도
시간 복잡도란,
문제를 해결하는데 걸리는 시간과 입력의 함수 관계를 나타내는 지표로,
주로 계수와 낮은 차수의 항을 제외시키는 빅-오 표기법을 사용한다.
프림 알고리즘은 구현에 사용되는 자료구조에 따라 시간 복잡도가 다르게 나타난다. 그래프의 특징에 맞게 자료구조를 선택하여 구현하면 될 것 같다.
| 자료 구조 | 시간복잡도 |
|---|---|
| 우선순위 큐 | |
| 인접 행렬 |
우선순위 큐의 경우는 모든 정점 개에 대해 탐색을 진행하며 각 정점마다 최소 간선을 탐색하기 때문에 의 시간이 소요된다. 또한 각 정점의 인접한 간선을 찾는 시간이 소요되기 때문에 가 된다. 일반적으로 가 보다 크기 때문에 가 된다.
인접행렬의 경우는 모든 노드에 대해 최소 간선을 탐색하기 때문에 의 시간이 소요된다.
💻코드 구현💻
import heapq
# 그래프 클래스
class Graph:
# 변수 정리
def __init__(self, v):
self.v = v #정점 수
self.edge = [[] for _ in range(v+1)] #간선 리스트
self.visit = [0]*(v+1) #방문 기록
# 간선 추가
def add(self, a, b, w):
self.edge[a].append((w, a, b))
self.edge[b].append((w, b, a))
# 프림 알고리즘
def prim(self, start):
self.visit[start] = 1 #출발 정점
result, mst = 0, []
candi = self.edge[start] #인접한 정점 리스트
heapq.heapify(candi) # 우선순위 큐
while candi:
w, a, b = heapq.heappop(candi)
if not self.visit[b]: # 방문 기록이 없다면 추가
self.visit[b] = 1
mst.append((a, b))
result += w
for e in self.edge[b]: # 추가된 정점의 인접 간선 탐색
# 방문하지 않은 정점과 연결된 간선 추가
if not self.visit[e[2]]:
heapq.heappush(candi, e)
return result# 예제
g = Graph(4)
g.add(1,2,2)
g.add(1,3,4)
g.add(2,3,5)
g.add(2,4,7)
g.add(3,4,10)
print(*g.edge[1:])
g.prim(1)
# [(2, 1, 2), (4, 1, 3)] [(2, 2, 1), (5, 2, 3), (7, 2, 4)] [(4, 3, 1), (5, 3, 2), (10, 3, 4)] [(7, 4, 2), (10, 4, 3)]
# 13