A TIME SERIES IS WORTH 64 WORDS: LONG-TERM FORECASTING WITH TRANSFORMERS

https://arxiv.org/pdf/2211.14730
https://github.com/yuqinie98/PatchTST

Introduction

목표

다변량 시계열 예측 및 자기 지도 표현 학습을 위한 Transformer 기반 모델 설계

논문의 제안 : PatchTST

• Patching
  시계열 데이터를 패치로 분할하여 Transformer에 입력 토큰으로 제공함
  단일 시간 포인트 데이터는 문맥적 의미 정보를 유지하지 못하기 때문에 패치를 통해 지역적 의미 정보를 강화하고 전역적인 의미 정보를 포착함

• Channel-independence
  각 채널이 동일한 임베딩과 Transformer 가중치를 공유함
  다중 채널을 가지는 다변량 시계열 데이터의 채널 독립성은 각 입력 토큰이 단일 채널의 정보만 가지도록 하는 방식임

PathTST의 장점

• 시간 및 공간 복잡성 감소: 기존 Transformer는 입력 토큰 수 N에 대해 복잡도가 $O(N^2)$ 이지만,  패칭을 적용하면 $N≈L/S$ 로 크게 줄일 수 있음.

• longer look-back window 학습 능력: look-back window 길이 ($L$)을 늘리면 MSE를 0.518에서 0.397로 감소시킬 수 있는데, 패칭을 통해 입력 토큰 길이를 줄이는 방식을 통해 효과적으로 $L$ 길이를 늘릴 수 있음

  💡 look-back window 시계열 예측 모델에 입력으로 제공되는 과거 데이터의 길이 모델이 미래 값을 예측하기 위해 참고하는 과거 데이터의 범위를 나타냄

• 표현 학습 능력: Self-Supervised Learing 활용하여 선형 모델보다 더 높은 표현력을 학습함

Related Work

Patch in Transformer

• BERT (NLP) : character(문자) 기반 토크나이제이션 대신 subword 기반 토크나이제이션을 적용함

• ViT (CV) : 이미지를 16×16 패치로 분할하여 Transformer에 입력함

• BEiT, MAE와 같은 최신 작업은 모두 패치를 입력으로 사용함

Transformer-based Long-term Time Series Forecasting

기존 어텐션 메커니즘의 복잡성을 줄여 롱 시퀀스에서 더 좋은 성능을 보였으나, 대부분의 모델에서 point-wise 어텐션을 사용함.

• LogTrans : 컨볼루션 셀프 어텐션 레이어와 LogSparse 설계를 사용하여 키와 쿼리 간 point-wise 곱셈을 피했지만, 여전히 단일 타임 포인트에 기반한 설계임

• Autoformer : decomposition & auto-correlation 아이디어를 차용하여 전통적인 시계열 분석 방법론을 통합하였음. 패치 수준의 관계 정보를 위해 auto-correlation을 사용하지만, 완전 자동화된 설계를 달성하지 못함

• Triformer : 패치 어텐션을 제안했지만, 이는 패치 내 의미적 중요성을 드러내거나 입력 단위로 취급하지 않고 단순히 pseudo timestamp를 쿼리로 사용하는 방식임

Method

• 문제 정의: 다변량 시계열 샘플 집합의 각 샘플 look-back window $L$ $(x_1, ..., x_L)$이 주어졌을 때, 미래 $T$개의 값 $(x_{L+1}, ..., x_{L+T})$을 예측함
  ($x_t$ : $t$ 시간에서의 $M$ 차원 벡터)

• 인코더 구조는 vanilla Transformer를 사용함

Model Structure

Forward Process

1. $i$-번째 채널의 길이가 $L$인 단일 변수 시계열을 $x^{(i)}_{1:L} = (x^{(i)}_1, ..., x^{(i)}_L)$ 로 정의함
   $(i = 1, ..., M)$

2. $M$개의 단일 변수 시계열로 분할된 입력 $(x_1, ..., x_L)$은 Transformer 백본에 독립적으로 입력하고, 예측 결과( $\hat{x}^{(i)} = (\hat{x}^{(i)}_{L+1}, ..., \hat{x}^{(i)}_{L+T}) \in \mathbb{R}^{1\times T}$) 를 얻음.

Patching

패치를 사용하면 입력 토큰 수가 $L/S$ 로 줄어들며, 이는 메모리 사용량과 attention 연산의 복잡도를 크게 줄입니다($S$ 비율만큼 감소). 따라서 더 긴 데이터를 처리할 수 있어 예측 성능이 향상됨

각 단일 변수 시계열 $x^{(i)}$는 overlapped 패치 또는 non-overlapped 패치로 나뉨.

• 패치 길이를 $P$, 스트라이드를 $S$라고 할때, 패치 개수 $N = \lfloor (L - P)/S + 1\rfloor$인,
  패치 시퀀스 생성 : $x_p^{(i)} \in \mathbb{R}^{P\times N}$

• 패치화 하기 전에 원래 시퀀스의 끝에 마지막 값 $x_L^{(i)} \in \mathbb{R}$ 을 $S$번 반복하여 패딩

Transformer Encoder

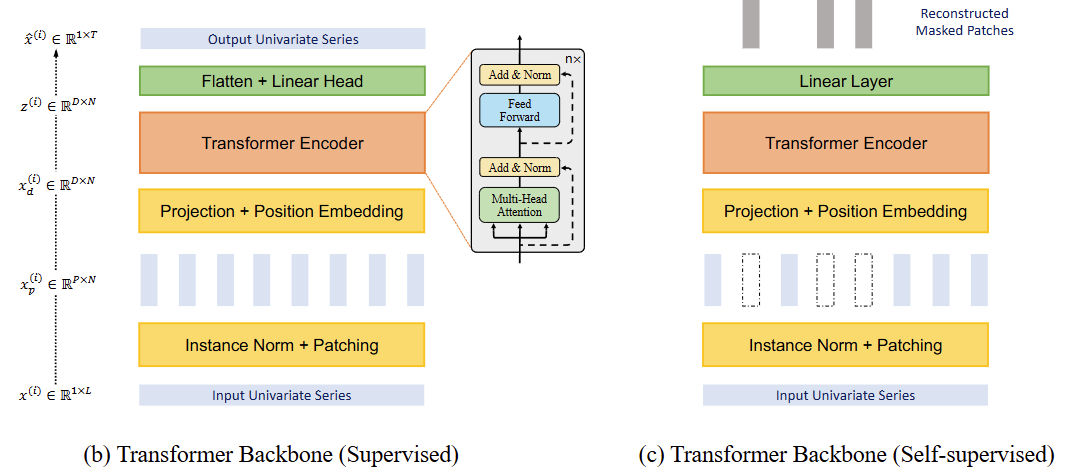
• 패치화된 데이터는 learnable linear projection ($W_p \in \mathbb{R}^{D\times P}$) 과 포지션 인코딩($W_{pos} \in \mathbb{R}^{D\times N}$)을 통해 $D$ 차원의 Transformer 잠재 공간으로 매핑됨.
  $x^{(i)}_d = W_p x^{(i)}_p + W_{pos}$, $x^{(i)}_d \in \mathbb{R}^{D\times N}$

• 멀티 헤드 어텐션의 각 헤드($h = 1, ..., H$)는 Query, Key, Value 행렬로 변환됨

  • Query : $Q_h^{(i)} = (x^{(i)}_d)^T W^Q_h$, ($W^Q_h \in \mathbb{R}^{D\times d_k}$)
  • Key : $K_h^{(i)} = (x^{(i)}_d)^T W^K_h$, ($W^K_h \in \mathbb{R}^{D\times d_k}$)
  • Value : $V_h^{(i)} = (x^{(i)}_d)^T W^V_h$, ($W^V_h \in \mathbb{R}^{D\times D}$)

• scaled dot-product 어텐션을 사용하여 최종 출력 $O_h^{(i)} \in \mathbb{R}^{D \times N}$ 계산

Loss Function

예측과 실제 값 간 차이를 측정하기 위해 평균 제곱 오차(MSE)를 사용함

Instance Normalization

• 훈련 데이터와 테스트 데이터 간 분포 이동 문제를 완화하기 위해 인스턴스 정규화를 적용함

• 각 시계열 인스턴스를 Z-score(평균 0, 표준편차 1) 정규화함

• 패치화 하기 전에 정규화를 하고, 예측 출력에 다시 평균과 표준편차를 더함

Representation Learning

단일 시간 포인트 Masked Encoder 문제점

1. 단일 시간 단계 수준에서의 마스킹
   • 마스킹된 단일 데이터 포인트 값은 전후 값들의 상관 관계를 통해 쉽게 추론할 수 있음.
   • 전체 시퀀스에 대한 높은 수준의 이해를 학습하지 못함
2. 출력 레이어 설계 문제
   • 모든 $L$ 시간에 해당하는 표현 벡터 $z_t ∈ \R^D$를 출력 레이어에 매핑하려면, $M$개의 변수 각각이 예측 길이 $T$를 가지는 linear map은 $(L⋅D)×(M⋅T)$ 크기의 매개변수 행렬 $W$가 필요함
   • 이런 행렬에서는 하나의 요소라도 값이 너무 커지면 과대 설계될 가능성이 있으며, 다운스트림 학습 샘플이 부족할 경우 오버피팅을 초래할 수 있음

PatchTST

• prediction head는 제거하고, $D×P$ 사이즈의 선형 레이어로 대체 함.
• 겹치는 부분 없이 패치화 하여 마스킹된 패치 정보가 혼합 되지 않도록 보장함
• 패치 인덱스를 무작위로 선택하여 0으로 마스킹하고, 모델은 MSE 손실을 사용하여 마스킹된 패치를 복원하도록 훈련함
• 각 시계열이 공유된 가중치 메커니즘을 통해 상호 학습되는 고유한 잠재 표현(latent representation)을 가지게 됨

Experiments

Hyper-parameters

• Patch : 입력 시퀀스 길이는 512, 패치 크기는 12로 세팅해서 총 42개의 non-overlapped 패치 생성
• Masking : 패치의 40%를 0값으로 마스킹
• 100 에포크 동안 SSL 학습

Fine-tuning

사전 학습된 모델이 준비되면, 학습된 표현을 평가하기 위해 두 가지 방식으로 지도 학습을 진행하였음

• Linear probing : 모델에서 헤드를 제외한 나머지 부분은 고정(freeze)하고, 20 에포크 동안 학습
• End-to-end fine-tuning: 모델 헤드를 업데이트하기 위해 먼저 선형 프로빙을 10 에포크 동안 수행한 후, 전체 모델을 20 에포크 동안 학습

Comparison with Supervised Methods

• 아래 표는 PatchTST(fine-tunning, linear probing, 처음부터 지도 학습)와 다른 지도 학습 방법의 성능을 비교함
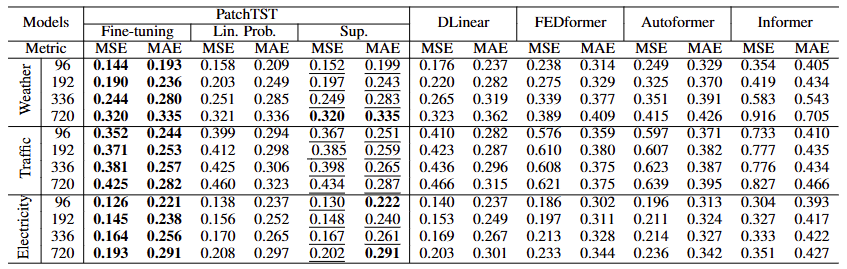
• 대규모 데이터셋에서 사전 학습 절차는 처음부터 지도 학습하는 것보다 더 좋은 성능을 보임