[논문 리뷰] Bimodal Masked Autoencoders

SungyunKim·2025년 4월 8일
ECGMAEmedical_AIpaper_reviewssl

paper_review

목록 보기
2/4

Abstract

ECG 분류를 위한 Bimodal Masked autoencoders with Internal Representation Connection (BMIRC)

  1. 주파수 스펙트럼을 MAE 사전 학습에 통합하여 ECG에 대한 포괄적인 이해 강화
  2. Internal Representation Connections (IRC)을 설정하여 인코더와 디코더의 표현을 연결하여, 디코더의 수행 능력 향상

Introduction

  1. 목표
  • ECG 심장 부정맥 감지를 위한 Self-supervised Learning
  1. Maked Autoencoders
    • MAE는 원본 데이터의 잠재적 특성을 탐색하여 모델이 이러한 판별 가능한 세부 사항을 학습하도록 돕습니다.
    • 인코딩 과정에서 점점 더 높은 수준의 정보로 표현하고, 디코딩을 통해 다시 저 수준 정보로 변환함. 그러나 인코더가 재구성에 지나치게 집중하게 되어 고수준 판별 표현을 학습하는 능력을 제한하게 되는 문제점이 있음
  2. BMIRC
    • 이산 푸리에 변환(DFT)을 사용하여 ECG를 주파수 스펙트럼으로 변환하고, 이를 독립적인 모달리티로 간주하여 타임 도메인 데이터를 보완함
    • Gated Representation Mixer (GRM)을 도입하여 인코더의 중간 레이어에서 추출한 표현을 디코더의 다양한 레이어에서 융합시킴. 이 과정을 IRC라고 명명함. 이 과정을 통해 디코더에게 다양한 수준의 정보를 제공하여 재구성을 지원하고, 인코더는 고수준의 판별 표현을 획득하도록 장려함

Related Works

1. Contrastive Learning based paradigm

CL은 불변성 제약 조건(imposition of invariance constraints)을 부여하여 표현 학습에 집중

  1. Time-Frequency Consistency(TF-C)
  2. Contrastive Predictive Coding(CPC)
  3. Time-Series Representation Learning Framework via Temporal and Contextual Contrasting(TS-TCC)
    • 시간적 불변성을 강조하며, 서로 다른 뷰에서 동일 시간 범위의 표현 간 유사성을 극대화하려고 합니다.
    • https://arxiv.org/pdf/2106.14112
  4. Universal Time Series Representation Learning(TimesURL)
    • 은 시간-주파수 기반 증강 기법을 도입하여 시간적 속성을 보존하며, 대조 학습과 결합된 최적화 목표를 통해 세그먼트 수준 및 인스턴스 수준 정보를 캡처
    • https://arxiv.org/pdf/2312.15709

2. Masked data modeling based paradigm

오토인코더를 사용하여 마스킹 되지 않은 데이터를 기반으로 마스킹된 데이터를 재구성하는 학습

  1. Patch Time Series Transformer(PatchTST)
  2. Time Series Masked Autoencoders(TimeMAE)

Method

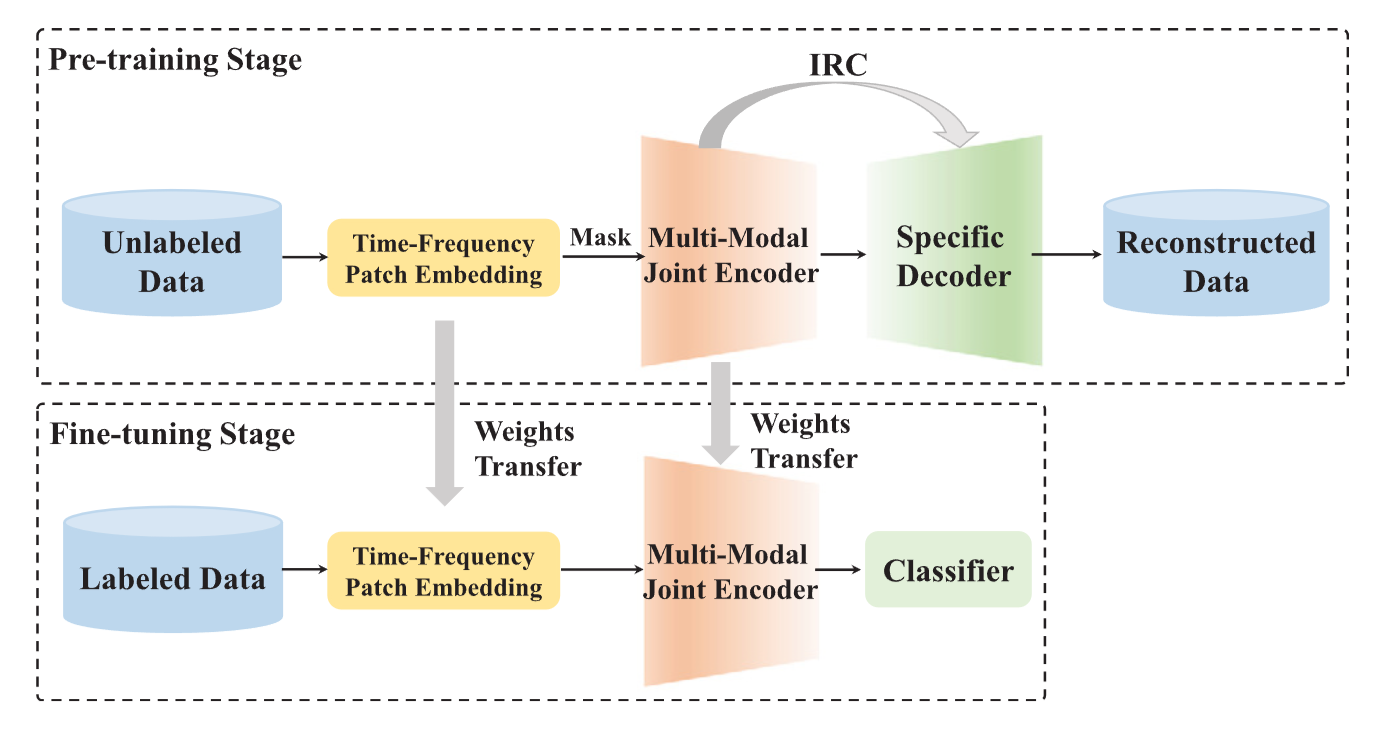
  1. 데이터셋이 원본 ECG만 제공한다고 가정할 때
  2. ECG와 주파수 스펙트럼의 패치 임베딩(시간-주파수 패치 임베딩) 생성
  3. 사전 학습 단계에서는 마스킹 후 시간-주파수 패치 임베딩이 이중 모달 공동 인코더(bimodal joint encoder)에 입력
  4. 모달리티별 디코더를 사용하여 내부 표현 연결(IRC)을 통해 마스킹된 데이터를 재구성합니다.
  5. 미세 조정 단계에서는 디코더가 global average pooling layer와 linear layer로 구성된 분류기로 대체

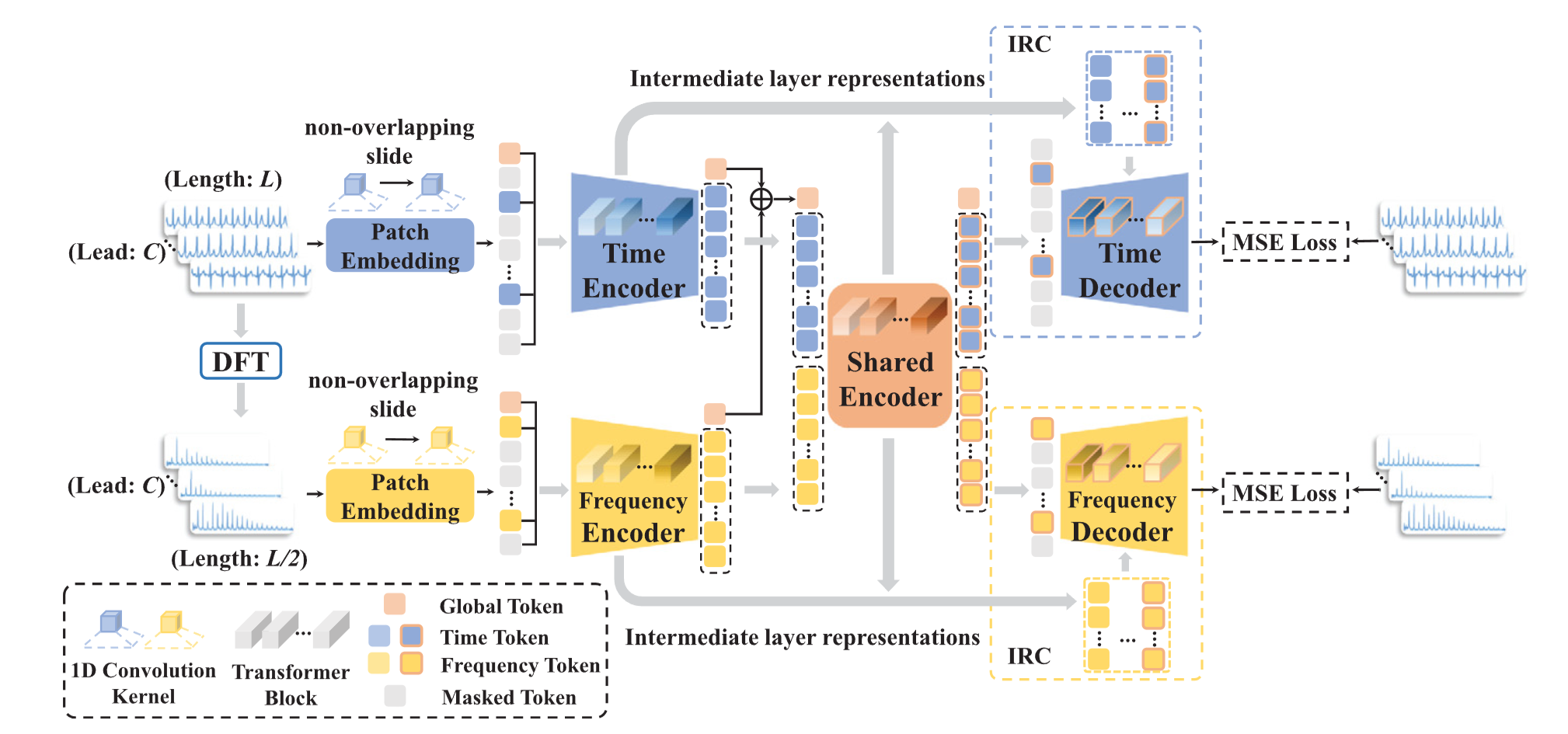
1. Time-Frequency Patch Embedding

Discrete Fourier Transform (DFT)

fi(k)=DFT[ti]=∑n=0N−1ti(n)⋅e−j2πNkn,k=0,1,…,N−1f_i(k) = \text{DFT}[t_i] = \sum_{n=0}^{N-1} t_i(n) \cdot e^{-j\frac{2\pi}{N}kn}, \quad k = 0, 1, \dots, N-1

  • n은 시간 지점의 인덱스를 나타내고, k는 ECG 내 다양한 주파수

  • 안티 앨리어싱(aliasing)을 방지하기 위해 DFT 변환 간격 N 의 길이는 ECG 길이 L 보다 크거나 같음 (N=L)

  • 주파수 스펙트럼의 대칭성을 고려하여 fif_i의 첫 번째 절반을 선택하여 중복성을 줄임 (fi∗∈RL/2f_i^∗∈R^{L/2})

Patch Embedding

  • 대부분의 방법이 시계열 데이터를 점 단위(point-by-point) 방식으로 처리하는 상황에서, 패치를 기반으로 한 모델링의 효과가 입증되었음. 마스킹된 포인트를 추론하는 것보다 마스킹된 영역을 학습하는 것이 더 어려운 태스크이며, 패치 기반 재구성 태스크는은 사전 학습된 모델이 더 많은 잠재적인 정보를 학습하도록 유도함

  • ECG(심전도)와 주파수 스펙트럼을 중첩되지 않는(non-overlapping) 패치로 나누어 인코딩함
    T=[t1,t2,…,tC]∈RL×CT=[t_1,t_2,…,t_C]∈\R^{L×C} , F=[f1∗,f2∗,…,fC∗]∈RL/2×CF=[f_1^∗,f_2^∗,…,f_C^∗]∈\R^{L/2×C}
    (C는 ECG 리드(lead)의 개수)

  • 두 가지 1D 컨볼루션 레이어를 사용하여 두 가지 모달리티에서 패치를 인코딩

  • 컨볼루션 커널 크기는 S×C 이고 stride는 S 로 설정되어, 개별 패치의 독립성 보장
    (각 패치의 길이는 S )

  • MAE(Masked Autoencoder)를 따르며, 패치 임베딩은 토큰으로 표시되며 각 토큰은 특정 패치에 대한 임베딩에 해당합니다. T와 F의 토큰은 각각 다음과 같이 표현됩니다:
    Zt=[z1t,z2t,...,zL/St]∈RL/S×D,Zf=[z1f,z2f,...,zL/2Sf]∈RL/2S×DZ_t=[z^t_1,z^t_2,...,z^t_{L/S}]∈\R^{L/S×D},Z_f=[z^f_1,z^f_2,...,z^f_{L/2S}]∈\R^{L/2S×D}
    (D는 컨볼루션 커널의 수. 즉, 각 모달리티의 임베딩 차원)

  • 명확성을 위해 ECG와 주파수 스펙트럼은 이후 섹션에서 각각 tt 와 ff로 표시함
    시간 및 주파수 모달리티에서 얻어진 토큰 수는 Nt=L/S,Nf=L/2SN_t=L/S,N_f=L/2S

2. Bimodal joint encoder

  • 모든 인코더는 동일한 구조의 Transformer 임.

  • learnable position embeddings (PEm∈RNm×DPE_m \in \R^{N_m \times D})과 패치 임베딩 합연산
    I~m=Zm+PEm\tilde{I}_m = Z_m + PE_m

  • 학습 가능한 전역 토큰 (zgm∈RDz^m_g \in \R^D)이 각 모달리티에 도입되며, 여기서 "g"는 "global"을 나타내며 전역 정보 추출을 용이하게 함. 마지막으로 모달리티 m∈{t,f}m∈\{t,f\}에 대해 입력 토큰 Im∈RNm×DI_m∈\R^{N_m×D}는 다음과 같이 표현됨
    Im=Concat(zgm,I~m)I_m = \text{Concat}(z_g^m, \tilde{I}_m)t

Masking strategy

  • 각 토큰이 동일한 확률로 랜덤하게 마스킹 되는 랜덤 마스킹 전략 채택하여, 다양한 배치와 에포크에서 수행되는 재구성 작업에 변동성이 생기게 만들었음

  • 시간 및 주파수 모달리티의 데이터 특성이 다르기 때문에, 실험을 통해 ECG에는 50%, 주파수 스펙트럼에는 75%의 마스킹 비율 채택.

  • ECG가 주파수 스펙트럼보다 더 복잡하다는 점을 고려할 때, 상대적으로 낮은 마스킹 비율을 사용하면 모델 성능이 향상됨

Overall structure

  • 모달리티 별 인코더에서는 각 모달리티 내 표현을 모델링하고, 공유 인코더에서 두 모달리키 간 상호작용을 캡처

  • 시간 및 주파수 모달리티의 입력 토큰은 모달리티별 인코더 EmE_m에 입력되어 출력 표현 OmO_m을 생성함
    Om=Em(Im)O_m = E_m(I_m), m∈{t,f}m∈\{t,f\}

  • 공유 인코더에 전달되기 전에, 각 모달리티의 토큰은 레이어 정규화(LN)를 거쳐 초기 융합 수행

  • 시간 및 주파수 모달리티의 전역 토큰(global tokens)이 추가되어 시퀀스의 첫 번째 위치에 삽입되며, 나머지 토큰은 순차적으로 연결(Concat)함

  • 마지막으로 공유 인코더에서 self-attention을 이용해 bimodal 표현 간 심층 융합 수행
    OmO_m : 모달리티별 인코더 최종 레이어의 출력 표현 
    OSO_S : 공유 인코더의 출력 표현

    O0S=[ogt+ogf,o~1t,o~2t,…,o~Ntt,o~1f,o~2f,…,o~Nff]O_0^S = [o_g^t + o_g^f, \tilde{o}_1^t, \tilde{o}_2^t, \dots, \tilde{o}_{N_t}^t, \tilde{o}_1^f, \tilde{o}_2^f, \dots, \tilde{o}_{N_f}^f]
    OS=Θ(O0S)O_S = \Theta(O_0^S)

3. Internal Representation Connections (IRC)

  • 디코더들은 모두 트랜스포머 블록으로 구성되며, 인코더보다 작은 차원과 적은 레이어를 가지는 얕은(shallow) 구조

  • MAE 에서는 인코더 최종 레이어의 표현만 디코더로 전달되지만, 우리는 디코더가 점진적으로 재구성을 완료할 수 있도록 인코더 중간 레이어에서 더 많은 표현을 제공함 (IRC)

  • IRC는 디코더의 재구성 부담을 완화하여 인코더가 재구성보다는 판별 표현 학습에 집중할 수 있도록 하며, 결과적으로 이는 고수준 판별 표현 획득 능력을 향상시킴

  • 공유 인코더의 출력 표현 OSO_S는 시간 및 주파수 모달리티에 대해 각각 OtO_t와 OfO_f로 분할됨

  • OtO_t와 OfO_f는 차원을 줄이기 위해 layer normalization-linear module을 거친 뒤 학습 가능한 위치 임베딩과 함께 마스킹된 토큰과 연결되어 모달리티별 디코더에 입력됨
    (첫 번째 디코더 레이어에는 IRC 적용 안함)

Gated Representation Mixer (GRM)

디코더의 깊이가 HH라고 가정할 때, 우리는 인코더에서 H−1H-1개의 표현 [V1m,V2m,…,VH−1m][V_1^m, V_2^m, \dots, V_{H-1}^m] 을 균일하게 선택하여 GRM으로 융합함

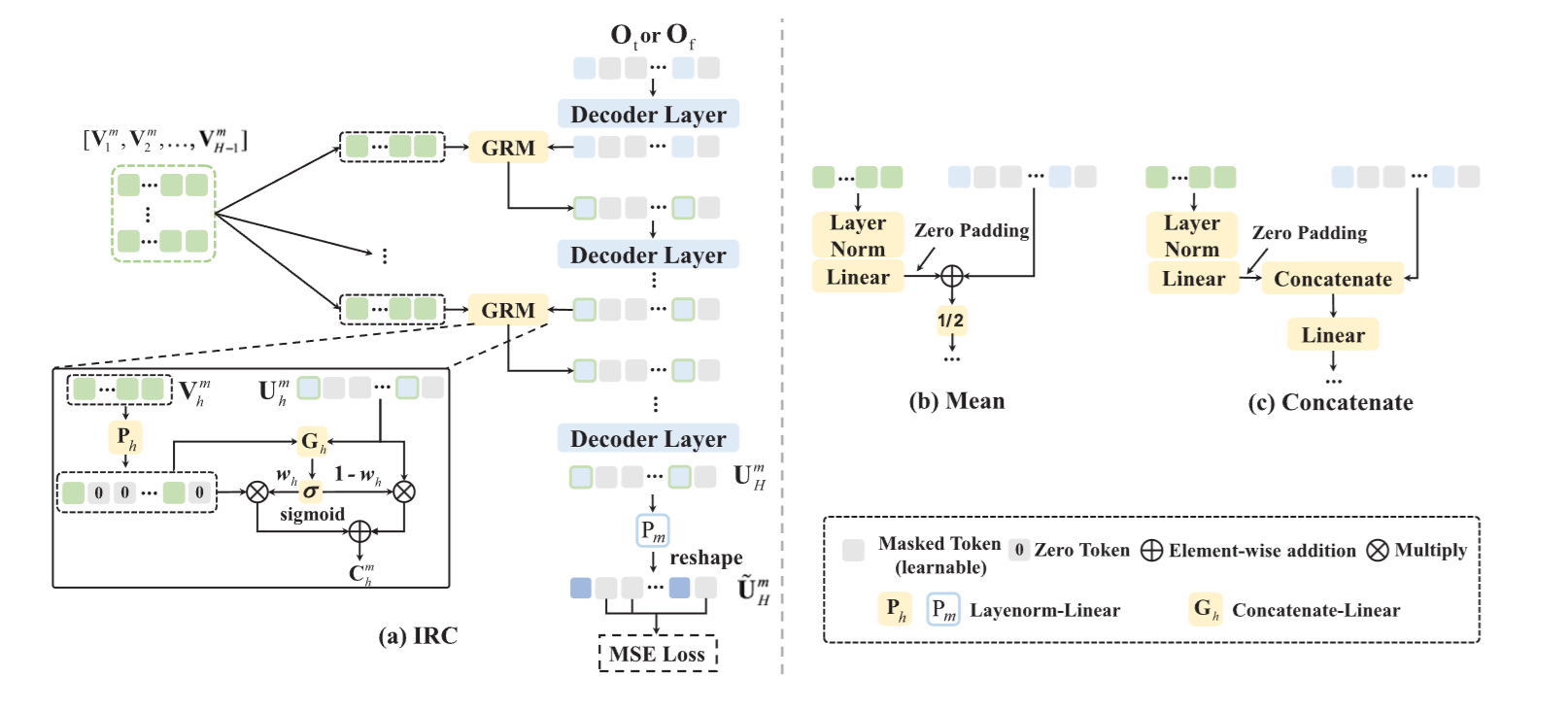
  • 모달리티 mm에 대해 디코더의 hh-번째 레이어에서 나온 표현 UhmU_h^m는 게이트 메커니즘을 통해 인코더의 hh-번째 표현 VhV_h 와 융합

  • 레이어 정규화-선형 모듈(layernorm-linear module, PhP_h)은 VhV_h 를 V~h\tilde{V}_h 로 변환하여 융합이 필요한 표현 간 정렬을 용이하게함

V~h=Ph(Vh)\tilde{V}_h = P_h(V_h)

  • 디코더 출력 UhmU_h^m는 학습 가능한 마스킹 토큰을 포함하므로, 일관된 차원을 유지하기 위해 V~h\tilde{V}_h의 해당 위치를 0 토큰으로 채움

  • 게이트 유닛 GhG_h 는 연결(concatenation)과 선형 변환(linear transformation)으로 구성되며, 입력 표현이 출력에 기여하는 비율을 제어함

  • 시그모이드 활성화 함수(σ)는 기여도를 대응하는 가중치 벡터 wh∈RNmw_h \in \mathbb{R}^{N_m}로 변환하고, 이는 각 토큰이 융합을 위한 가중치를 갖는다는 것을 의미함

wh=σ(Gh(V~h,Uhm))w_h = σ(G_h(\tilde{V}_h, U_h^m))
  • 토큰 수준에서, V~h\tilde{V}_h와 UhmU_h^m 는 각각 가중치 추가(weighted addition)를 통해 whw_h에 따라 맞춤형 융합 전략을 적용받게됨
Chm=wh∗V~h+(1−wh)∗UhmC_h^m = w_h * \tilde{V}_h + (1 - w_h) * U_h^m
  • 마지막으로 융합된 표현 ChmC_h^m는 (h+1)(h+1)-번째 트랜스포머 블록 Λh+1\Lambda_{h+1}에 전달되어 Uh+1mU_{h+1}^m 을 생성합니다.
Uh+1m=Λh+1(Chm)U_{h+1}^m = Λ_{h+1}(C_h^m)

Bimodal Reconstruction Loss

최종 디코더 레이어 출력 UHmU_H^m 를 얻은 후, 이는 레이어 정규화-선형 모듈 PmP_m 과 리셰이프(reshape) 작업을 통해 시간 또는 주파수 모달리티의 차원(RC×L\mathbb{R}^{C\times L} 또는 RC×L/2\mathbb{R}^{C\times L/2})에 맞게 변환.
(재구성 손실은 마스킹된 토큰에서만 계산함)

U~Hm=Reshape(Pm(UHm)),m∈t,f\tilde{U}_H^m = Reshape(P_m(U_H^m)), m \in {t, f}

Ltime=MSE(UHt,Tmasked)L_{time} = MSE(U_H^{t}, T_{masked})

Lfreq=MSE(UHf,Fmasked)L_{freq} = MSE(U_H^{f}, F_{masked})

Lrecon=αLtime+βLfreqL_{recon} = αL_{time} + βL_{freq}

( TmaskedT_{masked}와 FmaskedF_{masked}는 시간 및 주파수 모달리티에서 마스킹된 토큰의 ground truth, αα와 ββ는 두 모달리티의 재구성 손실 가중치 )

Experimental design

Datasets and metrics

  1. Ningbo
    • Ningbo First Hospital
    • 12lead, 500Hz, 10초
    • 34,905개
  2. PTB-XL
    • Physikalisch-Technische Bundesanstalt
    • 12lead, 500Hz, 10초
    • 21,837개
  3. Chapman
    • Chapman University 및 Shaoxing People's Hospital
    • 12lead, 500Hz, 10초
    • 10,247개
  4. Extravalidation
    • ECG 다중 라벨 데이터셋(Georgia 및 Hefei)
    • 두 데이터셋은 각각 10,344개와 20,335개의 샘플을 포함하며
    • 샘플링 속도는 동일하게 500Hz이고 각 샘플의 길이는 10초

Data preprocessing

  1. 노이즈 제거(Denoising)

    원본 ECG에서 흔히 발생하는 노이즈, 기준선 드리프트(baseline drift), 움직임 아티팩트(motion artifacts)는 모델의 분류 성능에 부정적인 영향을 끼침. 이를 완화하기 위해, 컷오프 주파수가 0.05Hz와 75Hz인 Butterworth 대역 통과 필터를 사용함

  2. 다운샘플링(Downsampling)

    계산 비용을 줄이기 위해 모든 ECG를 100Hz로 다운샘플링

  3. 정규화(Normalization)

    각 ECG 의 모든 리드에 인스턴스 정규화를 적용하여 분포 변화(distribution shift) 효과를 완화

  4. 라벨 재구성(Label Reconstruction)

    각 샘플에 할당된 SNOMED-CT 코드는 이산 카테고리 코드로 변환하였음

    • Ningbo 데이터셋: 25개
    • PTB-XL 데이터셋: 22개
    • Chapman 데이터셋: 19개
    • Georgia 및 Hefei 데이터셋: 각각 23개와 34개

    위 데이터셋은 클래스 불균형(class imbalance) 문제가 있으며, 이를 해결하기 위해 Fine-tuning 단계에서 클래스 가중치 전략을 채택했으며, 샘플 수가 적은 클래스에는 손실 계산 중 더 큰 가중치를 할당함

profile
SungyunKim
MedicalAI Researcher
이전 포스트

[논문 리뷰] Self-Supervised Learning for ECG

다음 포스트

[논문 리뷰] PatchTST

0개의 댓글