Selective Learning for Deep Time Series Forecasting

• Paper : https://arxiv.org/pdf/2510.25207
• Github : https://github.com/GestaltCogTeam/selective-learning
• NeurIPS 2025 (citation: 2)
• 요약
  • MSE 손실(loss)을 통해 모든 타임스텝(timestep)을 일률적으로 최적화하며, 불확실하거나 이상한 타임스텝들까지 차별 없이 학습하여 노이즈와 이상치에 취약한 시계열의 본질적인 특성으로 인해 과적합(overfitting)이 발생한다.
  • 최적화 과정에서 MSE 손실을 계산할 전체 타임스텝 중 일부를 선별하며, 모델이 일반화가 불가능한 타임스텝은 무시하고 일반화 가능한 타임스텝에 집중하도록 유도하는 '선택적 학습(selective learning)' 전략을 제안한다.
  • 불확실한 타임스텝을 필터링하는 불확실성 마스크(uncertainty mask)와 이상 타임스텝을 제외하는 이상치 마스크(anomaly mask) 이중 마스크(dual-mask) 메커니즘을 도입하였다.

Introduction

Problem

산업용 센서는 기계적 진동이나 전자기 방해에 쉽게 영향을 받으며, 주식 가격은 정책 개입에 따라 비정상적인 변동을 보인다. 이러한 간섭 요인들은 노이즈와 이상치(anomalies)로 인한 과적합(overfitting) 문제를 야기한다.

기존 손실 함수(MSE, MAE)는 각 타임스텝을 동일하게 취급하여 계산한다. 이는 모델이 일반화될 수 없는 불확실하고 이상한 타임스텝까지 학습하게 하여 과적합 문제를 야기하고 모델의 성능을 저하시킨다.

Figure 1. (Right)과 같이 iTransformer 모델은 ETTh1 데이터셋으로 학습될 때 MSE loss가 세 번째 에포크 이후 다시 증가하며 과적합 되는 것을 볼 수 있다.

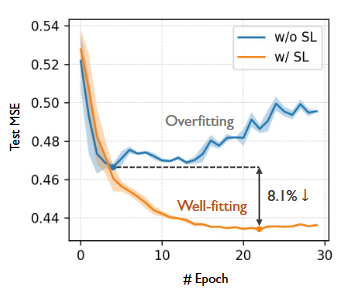
Figure 1. Right

Solution

이러한 문제를 해결하기 위해, 본 논문에서는 일반화 가능한 타임스텝만 최적화에 사용하고, 식별된 불확실하거나 이상한 타임스텝은 폐기하는 선택적 학습(selective learning)을 제안하며, 비일반화(non-generalizable) 타임스텝을 동적으로 필터링하기 위한 이중 마스크(dual-mask) 메커니즘을 도입하였다.

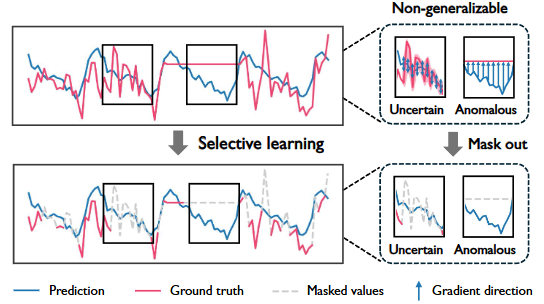
Figure 1. Left

모델의 일반화 성능을 저하시키는 두 가지 주요 타임스텝:

1. 불확실한(Uncertain) 타임스텝: 주로 노이즈(예: 신호 방해)로 인해 발생하며, 높은 예측 불확실성을 가진다. 결과적으로 gradients 업데이트가 무작위 방향으로 이루어져 노이즈에 원치 않게 적합되는 결과를 초래한다.
2. 이상(Anomalous) 타임스텝: 주로 예외적인 사건(예: 센서 오작동)에 의해 발생합니다. 모델의 예측은 확신이 있을 수 있으나 상당한 오차가 발생하며, 이는 모델이 인스턴스 특화된 특징을 학습하도록 강제하여 일반화를 저해한다.

Related Works

Deep Models

• Transformer 기반 모델: 장기적인 시간적 의존성
  • Informer : 2차 복잡도를 줄이기 위해 ProbSparse 어텐션을 도입하였다.
  • PatchTST : 시계열을 patch 단위로 나누고 channel-independent 전략을 사용한다.
  • iTransformer : 각 시계열을 독립적으로 변수 토큰(variate token)에 임베딩하고 셀프 어텐션을 적용하여 다변량 상관관계를 포착한다.
• CNN 기반 모델: 지역적 패턴 추출
  • TimesNet : 시계열을 2D 텐서로 변환하고 CNN을 사용하여 주기 내 및 주기 간 의존성을 포착한다.
• MLP 기반 모델: 가벼운 구조
  • DLinear : 분해(decomposition) 기법이 적용된 단순한 선형 레이어를 활용한다.
  • TimeMixer : MLP 레이어를 통해 다중 스케일(multi-scale) 정보를 포착한다.

Training Strategies

현재의 딥러닝 패러다임은 모든 타임스텝에 대해 일관되게 회귀 손실(예: MSE/MAE)을 계산하며, 다양한 대안 방법들이 존재하지만 특정 데이터셋과 시나리오에 최적화 되어 일반화되지 못했다.

• iTransformer : 대규모 다변량 시계열을 위해 변수의 서브셋을 무작위로 선택하는 학습 전략을 제안했다.
• Merlin : 데이터 누락에 대한 모델의 견고성을 높이기 위해 지식 증류(knowledge distillation) 전략을 채택 했다.
• MTGNN : 학습 중에 예측 길이를 점진적으로 늘려가는 커리큘럼 학습(curriculum learning)의 아이디어를 시계열 예측에 적용했다.

Method

Preliminaries

Notations

• $\mathbf{X}_{0:T} \in \mathbb{R}^{T \times N}$ : 전체 시계열 데이터
• $X_t \in \mathbb{R}^N$ : $N$개의 변수를 가진 다변량 시계열에 대한, $t$번째 타임스텝
• $\mathbf{X}_{t-L:t} = {X_{t-L}, X_{t-L+1}, \dots, X_{t-1}} \in \mathbb{R}^{L \times N}$ : 과거(look-back) 윈도우 크기가 $L$인 과거 시계열
• $\hat{\mathbf{X}}_{t:t+F} = {X_t, X_{t+1}, \dots, X_{t+F-1}} \in \mathbb{R}^{F \times N}$ : 예측 윈도우 크기가 $F$인 미래 값
• $\mathcal{D}_{train} = {(\mathbf{X}_{t-L:t}, \mathbf{X}_{t:t+F})}_{t=L}^{T-F}$ : 학습 데이터셋은 스트라이드가 1인 슬라이딩 윈도우
• $f(\cdot; \theta) : \mathbb{R}^{L \times N} \rightarrow \mathbb{R}^{F \times N}$ : 파라미터 $\theta$로 정의된 심층 신경망 모델
• $\eta$ : 학습률(learning rate)
• $\tau$ : 학습 중의 반복 횟수(iterations)

Problem Statement

최적의 예측값 $\hat{\mathbf{X}}_{t:t+F} = f(\mathbf{X}_{t-L:t}; \theta)$ 를 구하는 것이 목표이며, 평균 제곱 오차(MSE)는 예측값($\hat{\mathbf{X}}_{t:t+F}$)과 GT($\mathbf{X}_{t:t+F}$) 사이의 차이를 계산하며, $\theta$를 최적화하기 위해 사용되는 대표적인 손실 함수이다.

Selective Learning

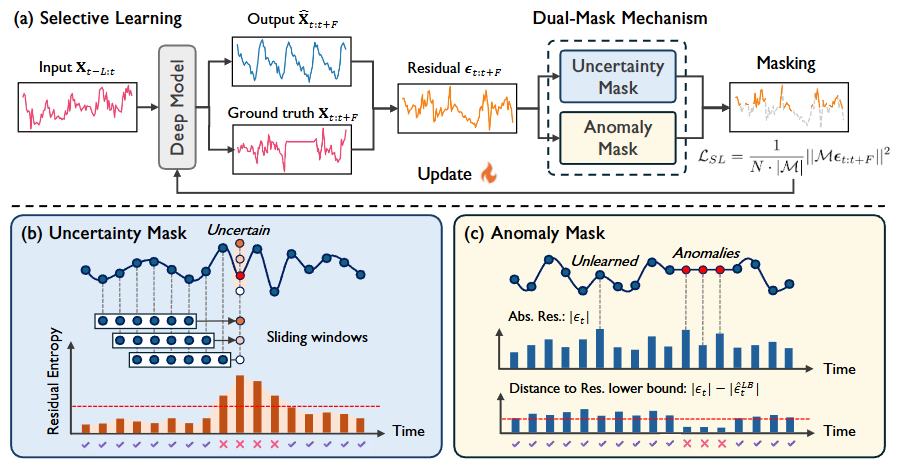
Figure 2. (a) Overall framework of selective learning. (b) Uncertainty mask. (c) Anomaly mask.

핵심 아이디어는 일반화 가능한 타임스텝의 서브셋에 대해서만 MSE 손실을 계산한다는 것이며, 두 가지 범주의 타임스텝을 마스킹하여 동적으로 필터링하는 이중 마스크(dual-mask) 메커니즘을 제안한다.

1. 불확실한(Uncertain) 타임스텝 : 모델이 예측한 값과 GT의 잔차(residual)를 이용해 잔차 분포의 엔트로피를 불확실성 척도로 사용한다. 슬라이딩 윈도우 샘플링을 통해 서로 다른 윈도우에서 예측된 타임스텝샘플들을 얻을 수 있으며, 이를 통해 잔차의 엔트로피를 정량화하여 높은 엔트로피를 가진 타임스텝을 걸러내는 지표로 활용한다.

2. 이상(Anomalous) 타임스텝 : 간단한 모듈을 추가하여 각 타임스텝의 잔차 하한(lower bound)을 구하도록 학습한다. 현재 잔차가 하한에 가장 가까운 타임스텝을 마스킹함으로써, 학습해야 할 타임스텝은 유지하면서 비일반화 이상치를 동적으로 제거한다.

   $\tau$번째 반복(iteration)에서의 시계열 예측 모델 $f(\cdot, \theta)$가 주어졌을 때, 비일반화 타임스텝의 서브셋에서만 최적화를 제한하는 마스크 $\mathcal{M}^{(\tau)} \in \{0, 1\}^F$를 만들어 손실 함수를 계산한다.

여기서 $\mathcal{M}^{(\tau)} = \mathcal{M}_u^{(\tau)} \lor \mathcal{M}_a^{(\tau)}$이며, $\mathcal{M}_u^{(\tau)}$와 $\mathcal{M}_a^{(\tau)}$는 각각 불확실성 마스크와 이상치 마스크를 $\lor$는 요소별(element-wise) OR 연산자를 의미한다. 또한 채널 독립(channel-independent) 전략을 채택하여 각 변수에 대해 독립적으로 마스크를 생성한다.

Uncertainty Mask

높은 예측 불확실성을 보이는 타임스텝을 위한 엔트로피 기반의 마스킹 접근법

$\epsilon_t = X_t - \hat{X}_t$를 $t$번째 타임스텝의 잔차라고 할 때, 각 타임스텝은 한 에포크 내에서 $n_t = \min\{t - L + 1, F\}$번 예측된다. 잔차는 가우시안 분포 $\epsilon_t \sim \mathcal{N}(\mu_t, \sigma_t^2)$를 따른다고 가정하며, 이에 따라 잔차 엔트로피와 분산은 다음과 같이 계산한다:

잔차 엔트로피가 상위 $r_u\%$인 타임스텝에 하드 임계값(hard thresholding) $\gamma_u$를 적용하여 불확실성 마스크 $\mathcal{M}_u^{(\tau)}$를 얻는다:

Anomaly Mask

이상 타임스텝은 일반적으로 실제값과의 편차로 인해 큰 잔차를 발생 시키기 때문에 단순히 잔차 $| \epsilon_t |$가 큰 타임스텝을 마스킹하는 방식은, 실제 이상치와 학습이 덜 되었지만 일반화 가능한 패턴을 구분하지 못한다는 한계가 있다.

이러한 한계를 극복하기 위해, 잔차와 이론적 하한(lower bound) $\epsilon_t^{LB}$ 사이의 편차인 $S(X_t)$를 정의한다:

따라서, 이상 타임스텝은 높은 잔차 하한을 가져 상대적으로 작은 $S(X)$ 값을 보이고, 학습되지 않은 타임스텝은 현재 잔차와 이론적 최소값 사이의 큰 격차로 인해 큰 $S(X)$ 값을 보인다.

잔차 하한(residual lower bound)을 추정하기 위해 학습 데이터셋 $\mathcal{D}_{train}$ 상에서 가단한 모델 $g(\cdot; \phi)$를 학습 시키고, 이를 통해 $\hat{S}(X_t)$를 다음과 같이 추정한다:

하드 임계값(hard thresholding) $\gamma_a$를 사용하여 $\hat{S}(X_t)$ 값이 가장 작은 상위 $r_u\%$의 타임스텝을 필터링해 이상치 마스크 $\mathcal{M}_a^{(\tau)} \in \{0, 1\}^F$를 얻는다:

특히, 추정된 잔차 하한을 정적(static)인 마스킹 기준으로 사용하지 않고, $S(X_t)$는 현재의 예측값에 따라 마스킹을 동적으로 조정할 수 있다. 이러한 방식은 두 가지 장점이 있다.

1. 편향 완화: 정적 마스킹은 학습 데이터셋 $\mathcal{D}_{train}$의 분포를 크게 변화시켜 편향(bias)을 유발하는 반면, 동적 마스킹은 학습 중에 마스크를 적응시켜 기대치(expectation) 측면에서 이러한 편향을 완화한다.
2. 점진적 학습: 일반화가 덜 되는 드물지만 중요한 극한 이벤트(예: 극단적 날씨)에 대해, 동적 마스킹은 먼저 일반화 가능한 타임스텝을 학습한 후, 이전에 이상치로 간주되었던 타임스텝들을 점진적으로 학습하도록 시도한다.

Experiments

실험 설정

• ILI 데이터셋의 경우 예측 길이 $F \in \{24, 36, 48, 60\}$,
  그 외 데이터셋은 $F \in \{96, 192, 336, 720\}$
• 하이퍼파라미터: 기존의 하이퍼파라미터 설정을 따르면서 마스킹 비율 $r_a$와 $r_n$만 조정
• 옵티마이저 : Adam

Main Results

SOTA 베이스라인 모델(iTransformer, TimeMixer)를 포함한 192개의 모든 케이스에서 성능이 향상됨

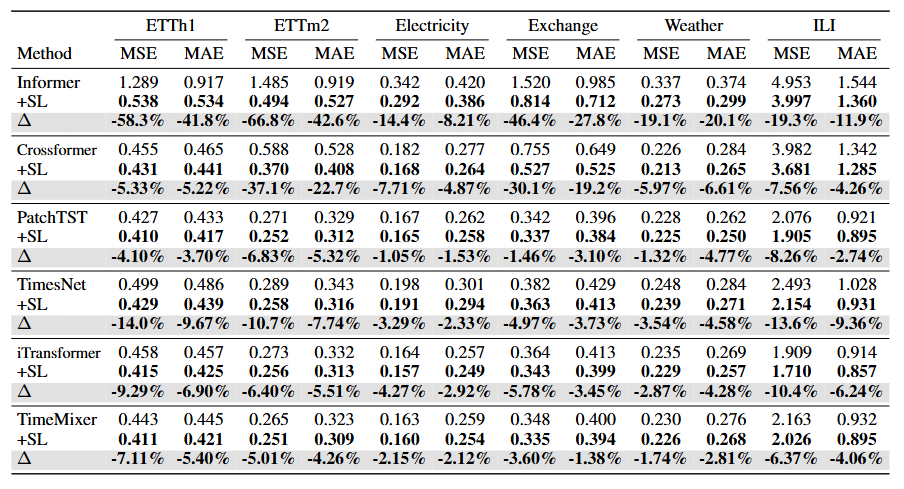
Table 1. main results

Zero-shot Forecasting

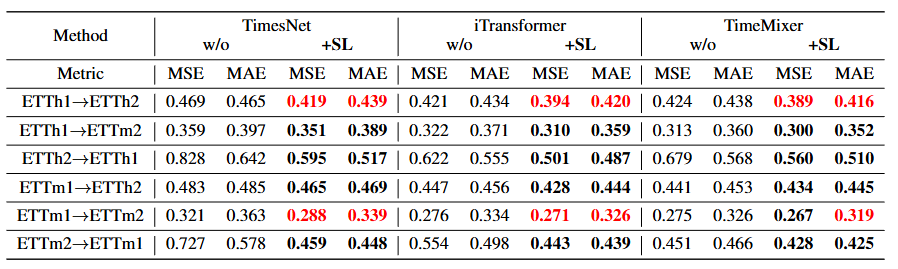
Table 2. zero-shot forcasting results

• 모델을 데이터셋 $\mathcal{D}_A$에서 학습시킨 후 추가 학습 없이 데이터셋 $\mathcal{D}_B$에서 평가했다.
• 어려운 시나리오(ETTh2 → ETTh1, ETTm2 → ETTm1)에서 선택적 학습은 평균적으로 MSE를 22.6%, MAE를 14.5% 감소시키며 상당한 개선을 이루었다.
• 일부 케이스에서는 타겟 데이터셋에서 처음부터 학습한(train-from-scratch) 결과보다 더 뛰어난 성능을 보이기도 하였다.

Comparison with Other Training Objectives

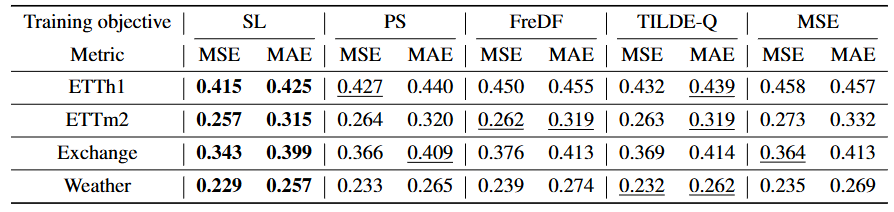
Table 3. Comparison between selective learning (SL) and other training objectives with iTransformer as backbone

• 선택적 학습은 높은 호환성을 가지기 때문에 모델에 완전히 무관(model-agnostic)하며, 다양한 정규화 방법이 적용된 어떠한 딥러닝 아키텍처에도 적용할 수 있다.
• 선택적 학습은 point-wise의 학습을 기반으로 하며, 형태 기반(TILDE-Q), 주파수 기반(FreDF), 분포 기반(PS loss) 목표를 포함한 point-wise가 아닌 대안적 학습 목표들과 비교했다.
• 타겟 시퀀스의 특정 타임스텝들이 본질적으로 일반화가 불가능하기 때문에 시간 또는 주파수 도메인에서 형태나 분포를 맞추는 전체 시퀀스에 대한 전역적 정렬(global alignment) 방식이 최선이 아님을 입증한다.

Ablation Study

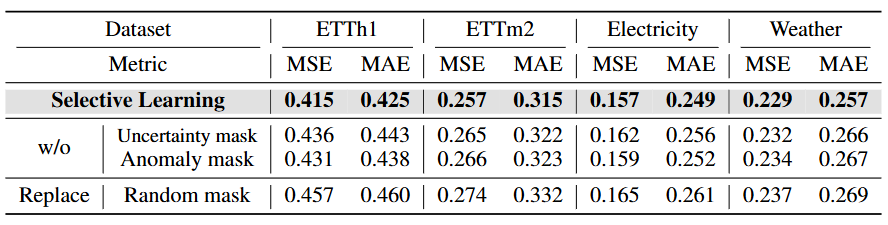
Table 4. Ablation results for selective learning with iTransformer as backbone

• 어느 한쪽 마스크라도 제거하면 4개 데이터셋 모두에서 상당한 성능 저하가 발생하며, 이는 두 마스크가 일반화 불가능한 패턴을 필터링하는 데 있어 필수적이고 서로 구별되는 기능을 수행함을 시사한다.
• 무작위 마스킹으로 대체하면 모델 성능이 마스킹을 하지 않은 경우와 비슷하거나 오히려 더 나빠지는데, 이는 단순히 타임스텝의 일부에 무작위로 주의를 기울이는 것만으로는 모델의 성능과 일반화 능력을 향상시킬 수 없음을 의미한다.

Hyperparameter Analysis

Effects of Masking Ratio

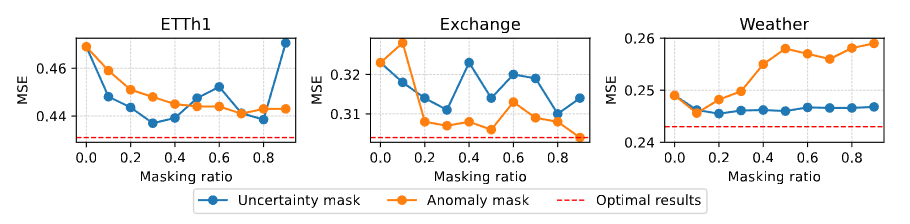
Figure 3. Forecasting results under different masking ratios. The prediction length is 336.

• 비정상성(non-stationary)이 강한 데이터셋(ETTh1, Exchange)에서는 더 큰 마스킹 비율이 우수한 성능을 보였다.
• 반면, 주기적인 패턴을 보이는 데이터셋(Weather)은 더 작은 마스킹 비율에서 향상된 성능을 보였다.
• 특히, Exchange 데이터셋의 경우 90%의 이상치 마스킹 비율에서 최고 성능을 보였는데, 이는 이 데이터셋에서 시장에 의한 일반화 불가능한 이상치가 노이즈보다 훨씬 더 큰 영향을 미치기 때문이다.

Effects of Estimation Model

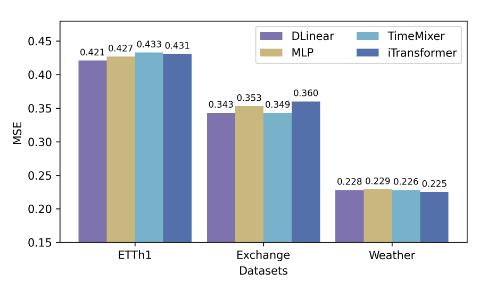
Figure 4. Forecasting performance with iTransformer as backbone and various estimation models. The results are averaged from all prediction lengths.

• 비정상성이 매우 높은 데이터셋(ETTh1, Exchange)에서는 단순한 모델이 우수한 성능을 보인 반면, 주기적 패턴을 보이는 데이터셋(Weather)은 더 복잡한 추정 모델이 유리했다.
• 그럼에도 불구하고, 추정 모델의 선택이 전체 성능에 미치는 영향은 제한적이었으며, 이는 선택적 학습의 견고성(robustness)을 강조한다.

Learning Curve Analysis

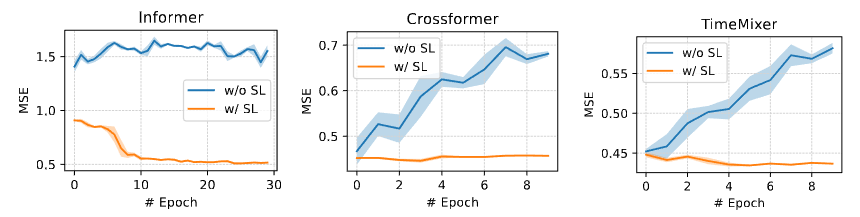
Figure 5. Test MSE curve on the ETTh1 dataset. The prediction length is 336.

• 비교된 세 모델 모두 다양한 정도의 과적합을 보이는 반면, 선택적 학습의 모델들은 안정적인 수렴과 우수한 성능을 달성하였다.