플로이드 워셜 알고리즘을 사용하는 문제.
다익스트라와 플로이드 워셜 알고리즘의 차이점.
다익스트라 : 특정 노드를 시작점으로 해서 나머지 모든 노드와의 최단 거리를 구함
플로이드 워셜 : 모든 노드를, 자신을 제외한 나머지 노드와의 최단 거리
그림에서 4에서 3으로 가는 화살표는, 4가 3을 이겼다는 뜻이다.
여기서 볼 때 순위를 확정할 수 있는 노드는 무엇일까?
2, 5이다.
4는 3,2,5보단 높겠지만, 1보다 높은지는 알 수 없다.
3 역시 2,5보다 높고 4보다 낮지만 1보다 높은지는 알 수 없다.
1은 3, 4보다 높은지 알 수 없다.
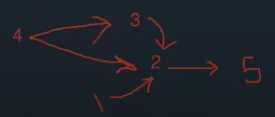
따라서 각 노드가 나머지 모든 노드들과의 최단거리를 구할 수 있다면 순위를 매길 수 있고, 나머지 노드들 중 하나와라도 최단거리를 구할 수 없다면 순위를 매길 수 없다고 결론 내릴 수 있다.
추가로 그림의 화살표와 같이 양방향이 아닌 단방향으로 가정하고 풀어야 한다.
주의 : 플로이드 워셜은 인접 리스트가 아니라 인접 행렬로 구현해야 한다.
아래는 코드이다.
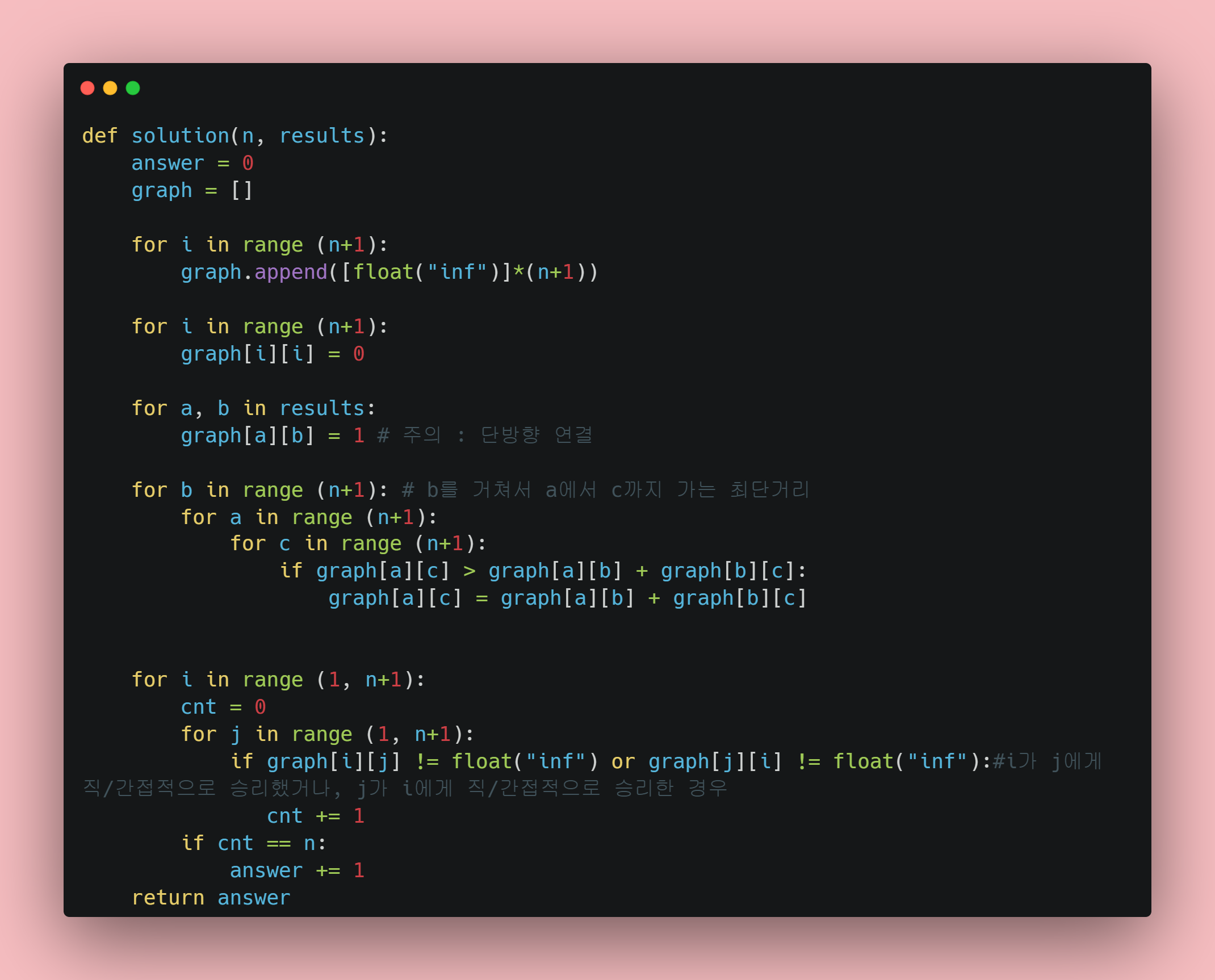
추가 설명 :
graph[i][j]값이 무한대가 아니라는 것은, i가 j를 직/간접적으로 이겼다는 뜻이다.
반대로 graph[j][i]값이 무한대가 아니라면, j가 i를 직/간접적으로 이겼다는 것이다.
그래서 if문을 통한 검증에서 or연산자로 graph[j][i]만 무한대가 아닌지만 확인할 것이 아니라, graph[i][j]도 무한대가 아닌지 확인해서 둘 중 하나라도 무한대가 아닌지를 확인해야 한다.
둘 중 하나라도 무한대가 아니라면 i,j 간의 대결에서 승패가 확정됐다는 뜻이다.
아래 내용은 해당 테스트 케이스를 가지고 visualization을 한 결과이다.
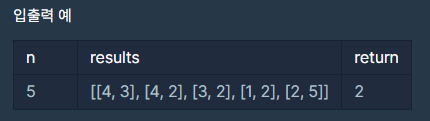
graph의 초기값이다. 모든 요소를 무한대로 설정하고,
i,j가 같은 경우, 내가 나 자신을 이긴 경우인데, 이 경우는 고려할 필요 없으니, graph[i][j]를 0으로,
result배열 값에 접근해서 i가 j를 이긴 경우 graph[i][j]값을 1로 업데이트 해준 상황이다.

플로이드 워셜 알고리즘을 사용해 최단거리를 업로드한 결과이다.
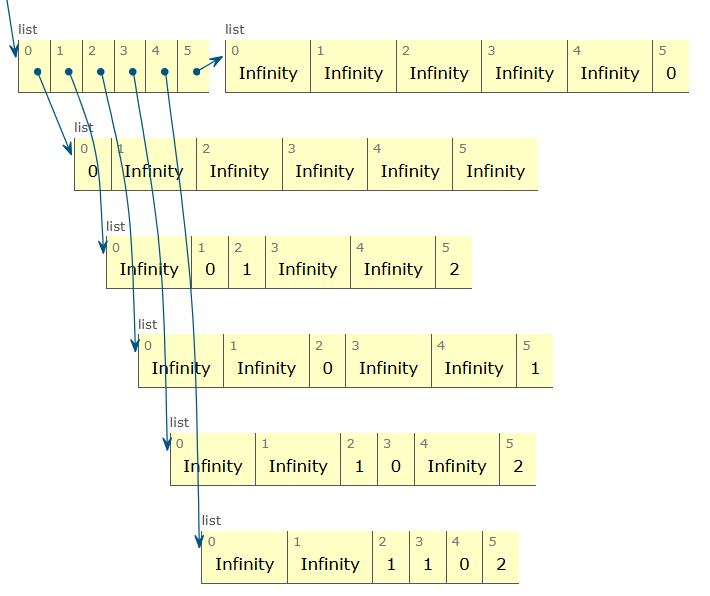
검증 차례인데, 검증 시 0열과 0행은 무시해도 된다.
인덱스 문제 때문에 1부터 값을 넣었기 때문에..
먼저 graph[2]를 본다. graph[2][0]은 무시하고(0열이니까), graph[2][1]은 무한대이지만, graph[1][2]은 1이므로 1이 2를 이겼다는 뜻 -> 1 2와의 대결에서 승패는 결정 났다는 뜻
graph[2][2]는 0이다. 자기 자신과의 대결은 무시한다.
graph[2][3]은 무한대이지만, graph[3][2]는 1이므로 2vs3 대결에서 3이 승리했다는 뜻.
graph[2][4]는 무한대이지만, graph[4][2]는 1이므로 4vs2대결에서 4가 승리했다는 뜻.
graph[2][5]는 1이므로 2vs5에서 2가 승리했다는 뜻이다.
=> 최종적으로 2는 자신을 제외한 모든 노드 1, 3, 4, 5와의 대결에서 승패가 확정났으므로 2의 순위를 확정할 수 있다.
같은 방법으로 graph[5]도 따져보면 5는 자신을 제외한 모든 노드들과의 대결에서 승패가 확정됐다.
따라서 2, 5번 노드의 순위를 확정할 수 있다.
