Binary Search Algorithm

1. 이진 탐색 알고리즘

1) 순차 탐색 vs 이진 탐색

• 순차 탐색 : 리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 확인하는 방법
• 이진 탐색 : 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법
  • 이진 탐색은 시작점, 끝점, 중간점을 이용하여 탐색 범위를 설정함

2) 이진 탐색 동작 예시

• 이미 정렬된 10개의 데이터 중에서 값이 4인 원소를 찾는 예시
• [Step 1] 시작점 : 0, 끝점 : 9, 중간점 : 4 (소숫점 이하 제거)
  
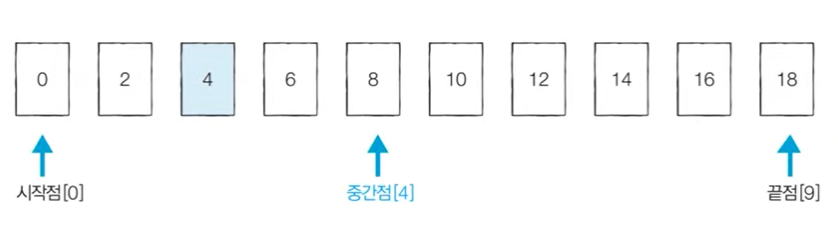
• [Step 2] 중간점에 있는 값인 8보다 4가 더 작기 때문에 왼쪽에서 다음 탐색을 수행
  
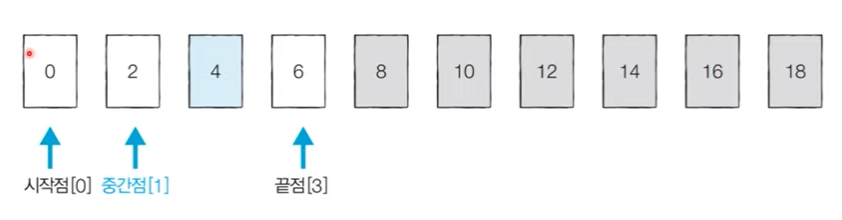
• [Step 3] 시작점과 중간점 위치가 같아지면 원하는 값을 찾은 것이므로 탐색을 종료함
  

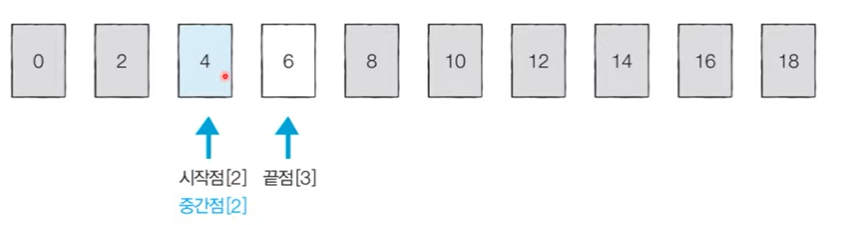
3) 시간 복잡도

• 단계마다 탐색 범위를 2로 나누는 것과 동일하므로 연산 횟수는 log2N에 비례함
• 이진 탐색은 탐색 범위를 절반씩 줄이며, 시간 복잡도는 O(logN)을 보장함

2. 이진 탐색 구현

1) 이진 탐색 재귀적 구현

# 이진 탐색 소스코드 구현 (재귀 함수)
def binary_search(array, target, start, end):
  if start > end:
    return None
  mid = (start + end) // 2
  # 찾은 경우 중간점 인덱스를 반환
  if array[mid] == target:
    return mid
  # 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
  elif array[mid] > target:
    return binary_search(array, target, start, mid - 1)
  # 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
  else:
    return binary_search(array, target, mid + 1, end)

# n(원소의 개수)과 target(찾고자 하는 값)을 입력 받기
n, target = list(map(int, input().split()))
# 전체 원소 입력 받기
array = list(map(int, input().split()))

# 이진 탐색 수행 결과 출력
result = binary_search(array, target, 0, n - 1)
if result == None:
  print("원소가 존재하지 않습니다")
else:
  print(result + 1)

10 7
1 3 5 7 9 11 13 15 17 19
4

10 7
1 3 5 6 9 11 13 15 17 19
원소가 존재하지 않습니다

2) 이진 탐색 반복문 구현

# 이진 탐색 소스코드 구현 (반복문)
def binary_search(array, target, start, end):
  while start <= end:
    mid = (start + end) // 2
    # 찾은 경우 중간점 인덱스를 반환
    if array[mid] == target:
      return mid
    # 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
    elif array[mid] > target:
      end = mid - 1
    # 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
    else:
      start = mid + 1
  return None

# n(원소의 개수)과 target(찾고자 하는 값)을 입력 받기
n, target = list(map(int, input().split()))
# 전체 원소 입력 받기
array = list(map(int, input().split()))

# 이진 탐색 수행 결과 출력
result = binary_search(array, target, 0, n - 1)
if result == None:
  print("원소가 존재하지 않습니다")
else:
  print(result + 1)

3. 파이썬 이진 탐색 라이브러리

1) 인덱스 반환

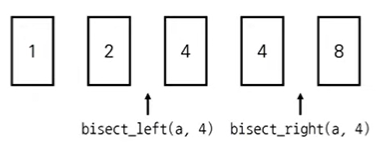
• bisect_left(a, x) : 정렬된 순서를 유지하면서 배열 a에 x를 삽입할 가장 왼쪽 인덱스를 반환
• bisect_right(a, x) : 정렬된 순서를 유지하면서 배열 a에 x를 삽입할 가장 오른쪽 인덱스를 반환
• 시간 복잡도 : O(logN)
  

from bisect import bisect_left, bisect_right

a = [1, 2, 4, 4, 8]
x = 4

print(bisect_left(a, x))
print(bisect_right(a, x))

2
4

2) 값이 특정 범위에 속하는 데이터 개수 구하기

from bisect import bisect_left, bisect_right

# 값이 [left_value, right value]인 데이터의 개수를 반환하는 함수
def count_by_range(a, left_value, right_value):
  right_index = bisect_right(a, right_value)
  left_index = bisect_left(a, left_value)
  return right_index - left_index

a = [1, 2, 3, 3, 3, 3, 4, 4, 8, 9]

# 값이 4인 데이터 개수 출력
print(count_by_range(a, 4, 4))
# 값이 [-1, 3] 범위에 있는 데이터 개수 출력
print(count_by_range(a, -1, 3))

2
6

4. Parametric Search

• 파라메트릭 서치란 최적화 문제를 결정 문제('예' 혹은 '아니오')로 바꾸어 해결하는 기법
  • 예시 : 특정한 조건을 만족하는 가장 알맞은 값을 빠르게 찾는 최적화 문제
• 일반적으로 코딩 테스트에서 파라메트릭 서치 문제는 이진 탐색을 이용하여 해결할 수 있음

이코테 이진 탐색 문제 풀이
이것이 취업을 위한 코딩 테스트다 with 파이썬