🖤 Introduction 🖤

📌 Motivation

A posture is defined as the skeletal configuration of a figure; for a realistic posture a set of criteria(제한조건) should be satisfied

→ 관절이라는 것은 조건을 만족해야한다
→ 너무 자유롭게 움직이면 사람처럼 보이지 않는다
→ 관절에서 팔꿈치가 뒤로 꺾이면 안된다

💁‍ 왜 IK가 필요할까?

✔ criteria(제한조건)

• Character models have natural articulation limits.
  → 관절이라는 것은 일정 각도 이상 꺾이지 못한다.
  
• Interpenetration of the body with other objects or themselves is not permitted.
  → 뚫고 들어가는 것이 불가능하다.
  
• Physical laws should be considered as well as numerous personal factors (height, length, etc.)
  → 물리적으로 타당한 움직임을 말한다.
  → 손을들어 올리면 다른 쪽이 균형을 맞추어서 내려가는 것 등이 존재하는데 사람마다 키, 체형이 달라서 하나로 통일되어 있지 않다. 이런 것들을 모두 고려해서 realistic posture을 만들어야 하는데 이것이 쉽지 않다.
  

⇒ 이걸 전부 디자이너가 처리하려면 너무 많은 시간과 노동력이 든다. 이를 자동으로 할 수 없을까?

✔ 일반적이지 않은 애니메이션의 필요

일반적인 에니메이션들을 많이 에셋스토어에 나와 있지만 검을 세번 휘드르고 찌르기를 만드고 싶은데 이런 애니메이션은 없어서 스스로 만들어야 한다. 덤블링 애니메이션을 만들고 싶은데 너무 어려움.

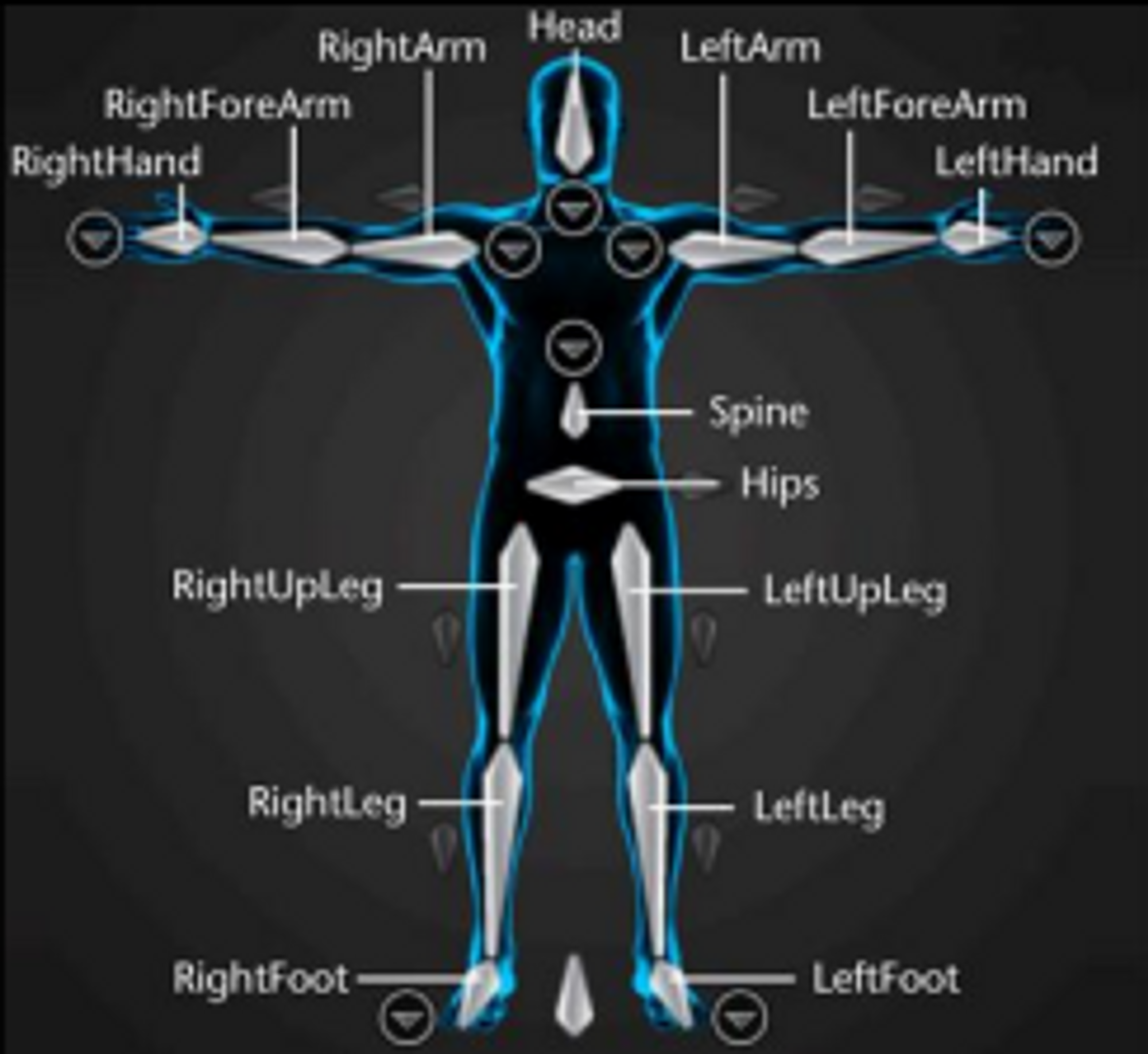
( 관절체 : 손, 발, 허리 , 머리 등을 가지고 있는 것 )

💁‍♀️ IK vs FK

✔ Inverse Kinematics (IK)

• Inverse Kinematics (IK) is a method for computing the posture via estimating each individual degree of freedom in order to satisfy a given task or criteria.
• 끝단(end effect)을 움직이면 나머지 관절체의 위치, 각도가 결정이 된다.
• end effecter : 물체를 집거나 결정을 할 때 가장 중요한 것은 끝단이다
• computer graphics, robotics, rehabilitation 등 여러 곳에서 사용 되고 있다.

✔ Forward Kinematics

• 관절 각각에 대해 위치와 회전값을 지정해주는 것.
  → joint가 60개,, 너무 어렵다 → IK가 나오게 된다!

---

📌 Brief review of IK

What id IK?
“Inverse kinematics positioning using nonlinear programming for highly articulated figures, 1994” solves the IK task as a problem of finding a local minimum of a set of non-linear equations, defining Cartesian space constraints.

✏ non-linear equations

• 문제를 풀 때 함수같은 것을 풀 때 linear하게 풀면 쉽다.
  → y = ax + b
  
• 해를 찾을 때 선으로 찾을 수 없고 복잡한 수식을 풀어야 할 때 non-linear라고 한다.
  → 관절체가 여러개가 있는데 관절체 하나 하나가 자신을 표현하는 수식들이 있다.
  → 이 수식을 모두 만족을 시키되 완벽히 만족을 시킬 수는 없다. 최대한 만족하는 방향으로 풀 건데 approximate를 때려서 풀게 된다.
  

✏ local minimum

• 관절체의 수식을 다 만족하는 것을 찾을 수 없다. 너무 오래 걸린다.
• 그래서 적당히 만족을 시키는 approximation을 찾고자 함.
• 그것이 어떻게 가능할까?
  → 우리는 게임에서 애니메이션이 적당히 잘 움직이면 눈치를 못해고 그냥 넘어간다. (팔꿈치가 살짝 올라가도 모름)
  → 즉, 너무 정확하게 만드는 것에 초점을 맞추지 않고 에러를 최소화하는 방향으로 문제를 풀겠다
  
• global minimum : 내가 조건들을 걸었을 때 이 조건들을 만족하는 가장 좋은 값
  → 이것을 찾는 것은 너무 힘드니 대충 주어진 상황에서 빨리 풀 수 있는 값들 중 괜찮은 것을 찾겠다!! 하는 것이 local minimum이다.
  

A spatial(공간상) constraints used in the paper involves two parts:

• One constraint is a character hierarchy with the end-effector (hand)
  → end effecter, 어깨가 얼만큼 움직이면 팔꿈치는 얼만큼 움직여야 하는지 등
  
• The other constraint is the position of the goal.
  → 목표를 다가가기 위해 최대로 노력하는 함수
  

+) Cartesian

• x, y 좌표계

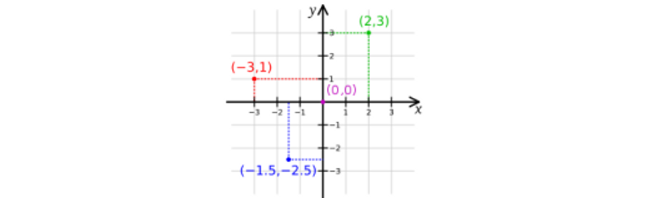
✔ Jacobian matrix

• non-linear 시스템 → 하나의 해를 찾을 수 없으니까 최대한 local minimum을 찾는 다고 이야기 했다. 이 때 사용하는 것이 자코비안 이다.
  In terms of IK problem, one of the popular numerical approaches is to use the Jacobian matrix to find a linear approximation to the solution.
  

• 해를 찾을 때 공간을 찌그러트려서 해를 찾으려고 노력하는데 이것이 일반적인 해를 찾는 시스템이다.

• Jacobian은 내가 관찰하는 시점에서만 가장 알맞은 친구를 찾겠어! 라는 아이디어를 가지고 만들어졌다

• 자코비안이 나왔다는 것은 관찰 가능한 정보들을 이용해서 approximaion할 생각이구나하고 이해하면 된다.

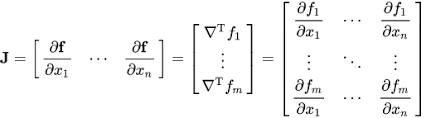
✔ IK의 발전 과정

1. Jacobian-based approaches suffer from high computational cost, complex matrix calculations and singularity problems. (It occurs when det(J) = 0)

   → complex matrix calculations : 편미분을 해야하니 자코비안은 컴퓨터 성능이 많이 필요.

   → singularity problems : 해가 풀리지 않는 것을 의미한다.

   해가 없다. 근데 순순히 죽어주지 않고 컴퓨터의 모든 자원을 다 끌어다 쓰고 수천 수만번 하고 나서 없는 것 같아 라고 말해버리게 된다.

   -> ex) 물건이 너무 멀어서 손이 닿지 않는다. 이 때 해가 없음이 나와야 한다. 이때 singularity 문제 발생

2. An alternative approach is given by ‘Inverse kinematic without matrix invertion, 2008’ where the inverse kinematics problem is solved from a feedback loop. This approach is computationally more efficient than the pseudo-inverse based methods and does not suffer from singularity problems

   • inversion 이 없는 IK
     → FK 내가 관절체에 모든 세타 정보가 주어졌을 때 Jacobian Matrix를 곱해서 최종 포지션 f를 만들겠다는 방향으로 진행이 된다.
     → 반면 IK는 반대다. end effecter의 포지션이 주어졌을 때 Jacobian을 이용해서 세타를 도출해는 것이 문제이다.

   즉 IK를 풀기 위해서는 자코비안의 inversion이 필요하다. $F = Jθ , J^{-1}F = θ$

   → singularity problem이 발생했을 때 "어 inversion이 없는데요?" 하고 죽어버리는 것이다.

   → 이 문제를 해결하기 위해 inversion 없이 문제를 해결하겠다는 방법이 나오게 된다

   • singularity problems 이 없음
   • 이전보단 빠르지만 자코비안이 들어가는 순간 느리다.

3. The use of IK solvers based on Newton methods is also popular. These algorithms seek target configurations by solving unconstrained nonlinear optimization problems.

   • 뉴턴의 방법 : 최적화 문제를 푸는 것, 자코비안 처럼 매트릭스로 푸는 것이 아니라 어떤 iteration을 통해 대략적으로 local minimum 하게 품
   • 당연히 IK를 풀 때는 constrain가 존재한다. return method가 조금 변형된 형태로 등장

4. Recently, numerous way of solving IK have been proposed such as non-iterative technique (FTL, FABRIK), motion capture data based IK, and deep learning based IK.

   • iteration을 돌리는 것도 느리니 FTL - "대충 이렇게 해도 돼" 느낌으로 게임에서 사용
   • FABRIK - 수도 알고리즘의 정점, 언리얼에서 사용하는 IK
   • motion capture data based IK
   • deep learning based IK - 로봇 공학 쪽에서 많이 사용

---

🖤 The Articulated Body Model 🖤

✔ The articulated body model

• In order to process the motion data, it requires to be preprocessed to ensure that the correct hierarchical connections and constraints are satisfied.
  관절체를 렌더링을 하기 위해서는 관절체에 대한 올바른 규격이 있어야 하고 규약에 따라 해야한다.
  
• In computer graphics applications, human body is defined by a complex hierarchical model consisting of many joints, each one having different degrees of freedom (DoF) and various possible restrictions.
  → Bone : joint 부터 joint의 연결
  → Joint : 관절체

  • 유니티나 언리얼에 가면 구조체의 형태로 어깨 안에 레프트 숄더,암, … 등등이 있는데 구조를 만든 이유는 어깨만 돌려도 나머지가 상호작용 하도록 만들기 위해 이런 구조체를 사용

  • root는 보통 배꼽정도를 말한다.
    → Dof(degrees of freedom) : 관절의 자유도

  • 어떤 관절은 벌어지는 것 밖에 안됨 : 1DoF

  • 이차원 평면 기준으로도 회전이 가능함 : 2DoF

  • 몇가지 축을 기준으로 회전하느냐에 따라 달라진다. 보통 DoF는 6까지 있다.

    → restrictions : DoF를 가지되 여기 이상을 못가게 막아두자는 것

✔ Human body modelling

• A rigid multibody system consists of a set of rigid objects, called links, connected together by joints. A joint is the component concerned with motion; it permits some degree of relative motion between the connected segments.
  → 우리의 몸은 강체이다
  rigid라는 하는 순간 물리 엔진이 쉬워진다. 우리 몸도 사실 완전 리지드는 아니지만 그러면 유체 모델 가져다 써야 하니 그냥 리지드라고 하자 큰 문제는 없다
  → set of rigid objects : 본들이 막대기 원기둥으로 이루어지는 등 우리가 흔히 하는 리지드 오브젝트들로 이루어짐
• 왼쪽은 휴먼 바디 모델을 표현하기 위한 최소한의 조인트
• 그치만 우리는 뼈 위에 살도 있는데 뼈만으로는 이를 표현하기 힘들 때가 있다
  → 그래서 이런 조직들을 또 따로 정의 하는 방식도 존재
  
• 루트로부터 바닥에 알 수 없는 조인트를 박아둔다.
  → 지면위에 있나? 구부정한 자세인가? 등을 체크하기 위해서
  
• 휴먼 바디 모델을 표현하기 위한 조인트들도 있지만 이와는 달리 별개로 정의된 조인트들도 있다.

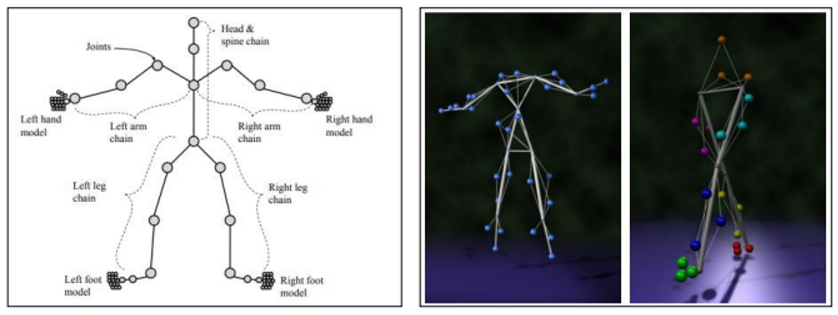
• A manipulator such as a robot arm or an animated graphics character is modeled as a chain composed of rigid links connected at their end by rotating joints
  → chain : 숄더를 움직이면 하위 조인트들이 다 움직이는 것

  • chain에 있는 것은 parent joint가 움직이면 children joint 은 다 움직임

    (end effecter사 가장 아래의 parent joint)
    

  • children이 움직인다고 parent가 움직일 필요는 없다

    → 그런데 IK에서 자식이 움직일 때 부모가 움직이는 경우도 존재. 부모와 자식 사이에 말도 안되는 constrained를 오버한 경우

• Any translation and rotation of the i-th joint affects the translation and rotation of any joint placed later in the chain.
  → 조인트가 엄청 많아서 i 번째로 표현
  → 어떤 거 열었는데 40개의 조인트 그러면 문서 같은 곳에 나와있음 1번이 뭐고 2번이 뭔지
  
• 적어도 하나 이상의 부모를 가지고 있어야 하고 자식의 수는 상관이 없다
• 조인트중에 자식이 없으면 end effecter라고 함

✔ DoF의 예시

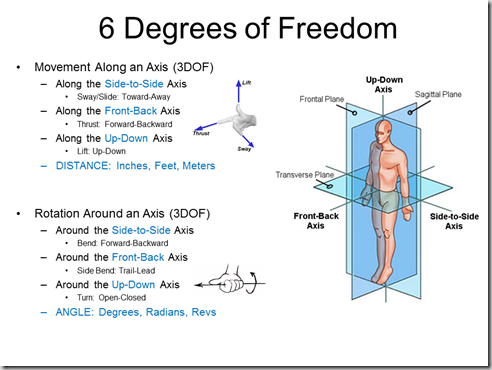
✔ Motion

rotational(회전) + translational(이동)이 합쳐져서 motion을 정의하게 됨

• Forward Kinematics (FK): 매프레임마다 관절체의 회전 위치 정보를 다 지정해줘야 한다
  → input으로 모든 joint angles를 넣는데
  → 퀄리티는 높지만 시간이 오래 걸림
  → Motion capture를 이용해 만드는 것은 일종의 FK 근데 살짝 고쳐 쓰고 싶을 때 IK를 사용하기도 함
  
• Inverse Kinematics (IK)
  → input으로 end effecter를 넣으면 알아서 된다.
  → 퀄리티는 낮지만 시간이 절약됨
  → 덤블링 같은 동작 말고 단순한 동작들에 많이 사용이 된다.
  

• FK는 unique solution이 존재
  관절체의 constraint만 지키면서 닿을 수만 있으면 항상 풀린다.
  
• IK는 항상 하나의 솔루션이 존재하진 않는다 → best solution을 찾는 것
  → 하나만 존재하는 경우 : 팔을 쭉 뻗었는데 딱 길이 맞을 때, 하나밖에 없다
  

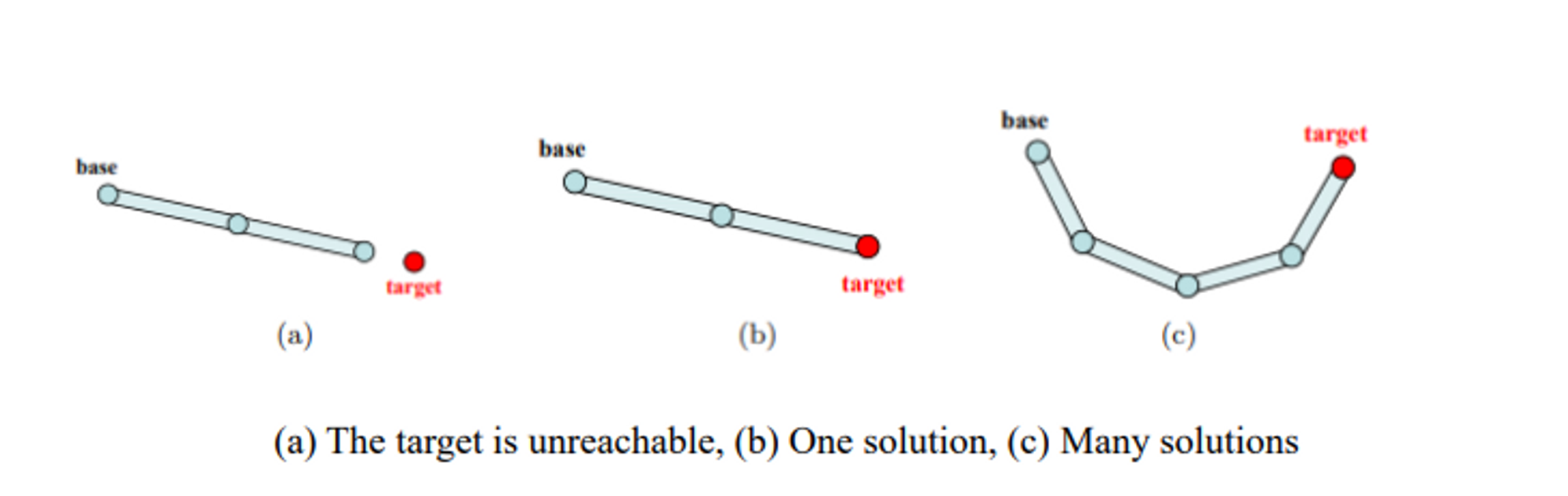
📌 Orientations and rotations

Geometric Algebra provides a convenient mathematical notation for representing orientations and
rotations of objects in three dimensions: Rotor (R)

• 축 회전을 더 편하게 하기 위해 등장함
• Rotor은 Geometric algebra의 한 종류

📌 Geometric algebra

• 기존 벡터들이나 수식으로 회전을 표현하는 것이 너무 어렵다. 이것을 편하게 하기 위해 등장하게 되었다.

---

🤍다음시간에는 IK를 이해하기 위한 Geometric algebra의 기초와 Rotor에 대해 알아보도록 하겠습니다.🤍

---

🖇 Reference

해당 포스트는 강형엽 교수님의 게임공학[GE-23-1] 수업을 수강하고 정리한 내용입니다.

[DoF] https://gunjanpatel.wordpress.com/2016/07/06/what-is-degrees-of-freedom-dof/