2. Geometric algebra & Quaternion

🖤 Geometric algebra 🖤
📌 Geometric Primitive in GA
✔ Bivector
0-dimensional object: scalar &1-dimensional object: vector.

2-dimensional object: bivector
- 공간을 감싸는 느낌의 벡터
- 이것의 넓이가 magnitute가 된다. 기존 벡터에서 magnitute와 방향이 같으면 같은 것이 되는데 bivector도 똑같다. 즉 차지하고 있는 방향과 가르키는 방향이 같으면 두 bivector는 같은 것이다.
⇒ 즉 벡터는 방향과 magnitude를 이용해 같고 다름을 정의한다.
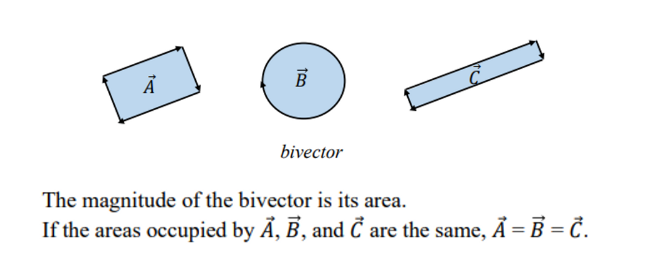
3D object: trivector & 4D object, and kD object can be defined.
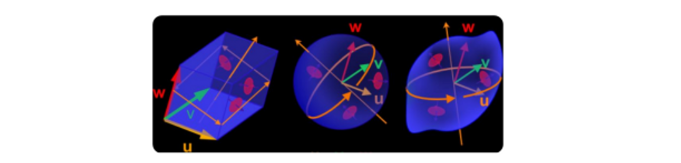
- 2d에서 bivector을 정의할 때는 왼쪽 회전 오른족 회전 두개 중 하나밖에 없으므로 magnitude가 중요했는데
- 3d에서는 회전 평면이 엄청 많아진다. 존재할 수 있는 평면 자체는 3d인데 bivector는 평면 위에 존재해야하니 이 평면이 어떤 orientation을 가지냐에 따라 달라진다.
- 스칼라 배를 하면 그냥 넓이가 스칼라배가 된다. (특징)
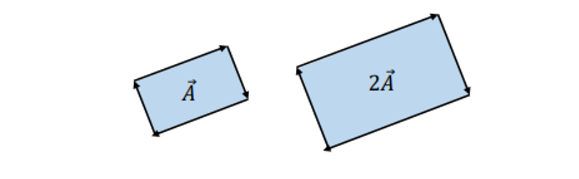
- bivector를 어떤 축을 기준으로 회전하는 것이라 생각하면 편하다
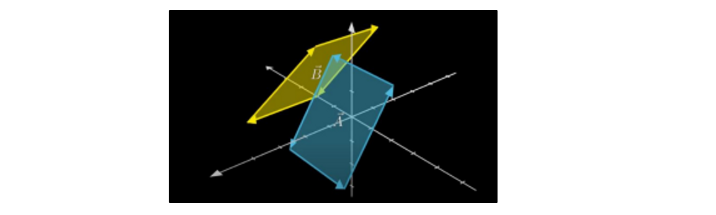
- 두개의 bivector가 합쳐지면 어떤 새로운 방향을 가진 bivector가 나온다
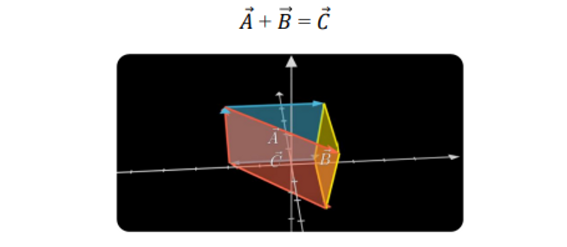
Basis Calculation
(2, 3, 4) → 2x + 3y + 4z ⇒ x를 basis라고한다.
- bivector도 basis로 표현할 수 있다.
[ there are three bivectors each represents an orthogonalplane in 3D space ]
- E3 와 E1 이 직교
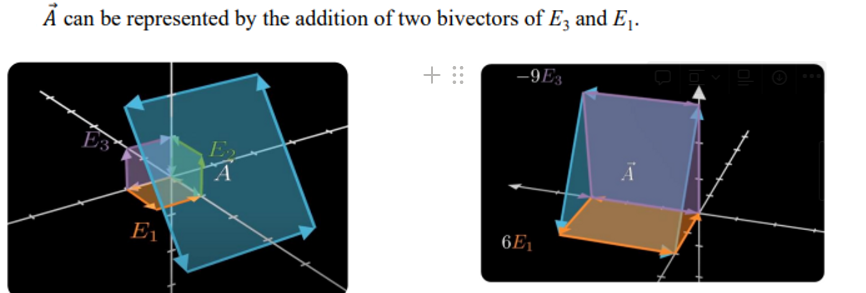
✔ Inner product (= dot product)
- 결과 : scalar Inner product result = length of the projection of one vector onto the other vector = scalar.
- 두 벡터 사이의 각도를 표현할 때도 많이 사용
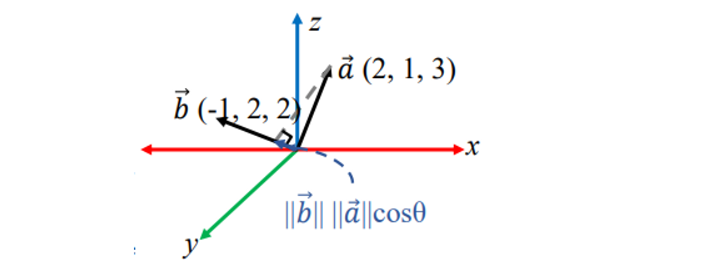
- The inner product of two vectors :
〈u, v〉 - 다음과 같은 법칙 성립
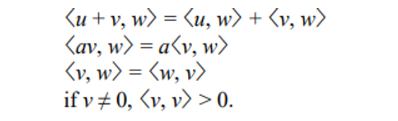
✔ Outer product = wedge product, exterior product
- 내적의 문제는 오리지널 벡터가 무엇이냐의 정보를 잃어버리는 것이었다.
- 둘 다 세타가 같다.
- 내적의 결과를 가지고 어떤 두 벡터의 연산인지 경우의 수가 많아 알기 어렵다
→ 2d에서는 그나마 조금 괜찮은데 3d에서는 더 알기 어렵다. 내적을 한 결과만으로 해당 벡터가 어디로부터 온 것인지 알기가 어렵다
=> 즉,계산 결과로부터 계산 전 벡터를 알기가 어렵다는 것이다.
u ∧ v
→ bivector을 만든다.
→ The orientation of the bivector : 먼저 온 u가 된다.
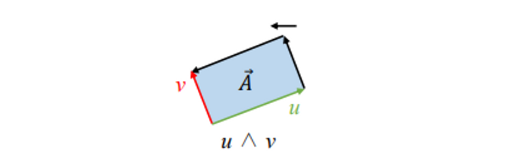
features
Anti-commutative
→ inner product는 A · B = B · A → 차이점!
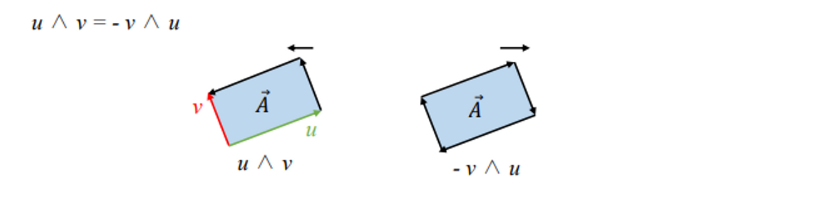
Associative (결합법칙)
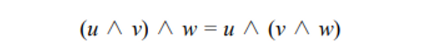
Distributive (분뱁법칙)
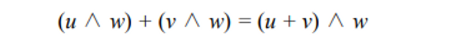
- Outer product of two parallel vectors = no parallelogram = 0 Therefore, the outer product of any vector with itself is zero.
→v ∧ v= 0 : 자기 자신의 외적은 0임 (외적은 sin 으로 표현이 되기 때문 )
→a · a=
- bivector ∧ bivector = trivector
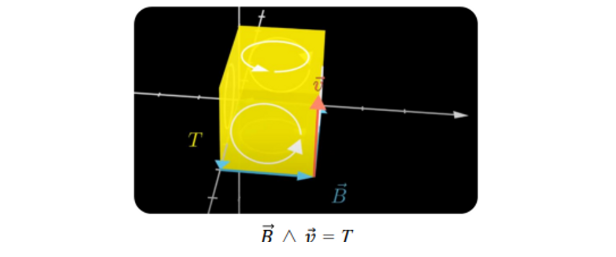
↪ Numerical explanation of the outer product
2 dimetional
Cartesian plane 에 해당하는 벡터를 unit vector를 사용해 basis로 표현한다
unit vector
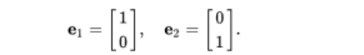
- 벡터를 unit vector로 표현
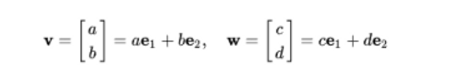
- 두 벡터가 이루는 parallelogram area = determinant
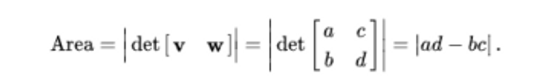
- the exterior product of v and w
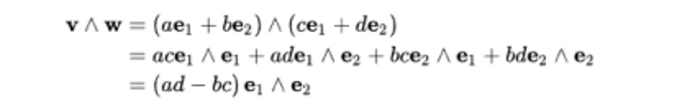
3-dimensional
- e1∧e2∧e3 ⇒ trivector
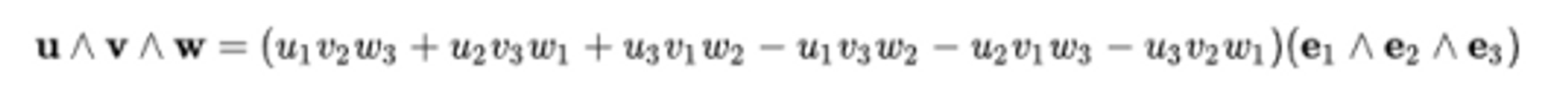
📌 Geometric Product
💭 Review of Inner product and outer product
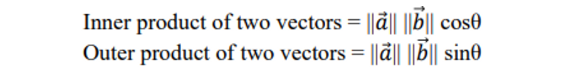
✔ Geometric Product의 등장 배경
- 내적은 어디서 왔느지 알 수가 없다. 각도만 같고 빙글빙글 돌리는 것이 모두 같은 값을 나타낸다. → 문제점
- 외적은 sin 을 사용해서 30도랑 -30도랑 결과가 달라진다. 주기함수이기 때문에 결과적으로 또 같아지는 부분이 발생한다.
⇒ 이를 해결하기 위해 Geometric Product 가 등장
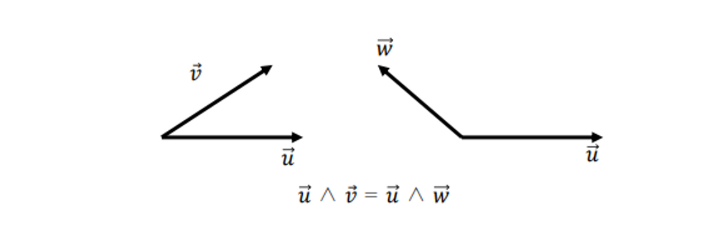
✔ Combining the inner product and outer product
- Adding the inner product and outer product
→ 기존의 product 개념과 다름
→ 어디서 오는지 명확히 알 수 있게 된다.
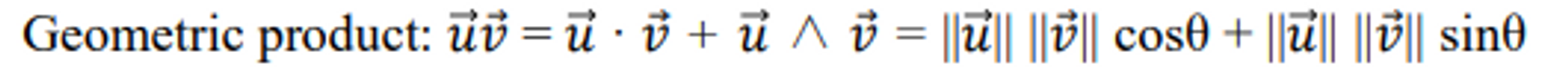
- 그런데 스칼라와 바이벡터를 더할 수 있는가?
→ 불가능하다
→ 이것을 가능하게 하기 위해 complex number 를 사용한다.
→
→ bivector 뒤에 i를 붙여서 문제를 해결한다.
✔ Understanding geometric product
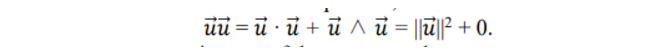
- The inverse of the vector
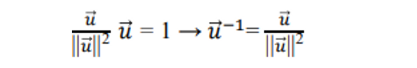
- uw와 순서를 바꾼 wu를 해주고 이 둘을 더한다
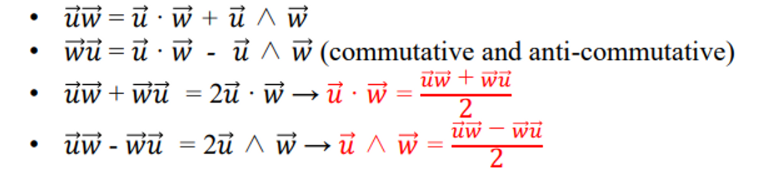
-
Geometric product of two different basis vectors is simply their outer product:
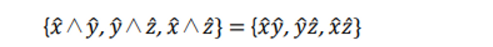
📌 Rotation with Geometric Algebra
✔ 2D geometric algebra
In linear algebra 2-dimensions: a vector is used and it has two components
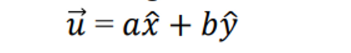
In geometric algebra in 2-dimensions: a multi-vector is used and it has four components
→ multi vector : V ( 스칼라 + 벡터 + 벡터 + 바이벡터)
멀티 벡터를 표현할건데 뭔지 잘 모르니까 표현가능한 친구들을 총집합 시키고 앞에다가 상수 붙여서 표현한 것이다.
→ 예를 들어 만약 상수가 없다면 a = 0으로 하여 필요한 것만 표기한다.
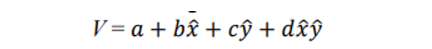
pseudoscalar 회전
- pseudoscalar
가장 높은 차원 수를 가지는 것에 대한 것
2d에서 highest-grade basis element는 다음과 같다
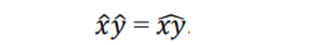
- 그리고 이것이 마치 허수처럼 등장을 한다. 이것들의 제곱이 -1이다.
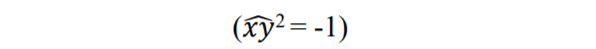
- i를 뒤에 박으면 positive / i를 앞에 박으면 negative 회전
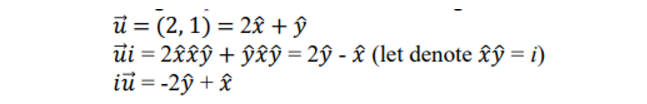
rotate a vector 𝑢 by an angle θ
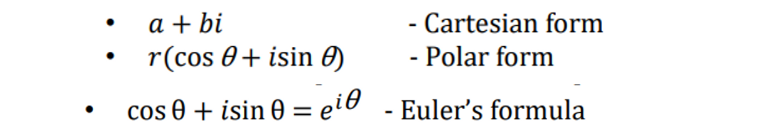
- θ 에 회전하고 싶은 값을 넣어서 직접 회전이 가능해진다
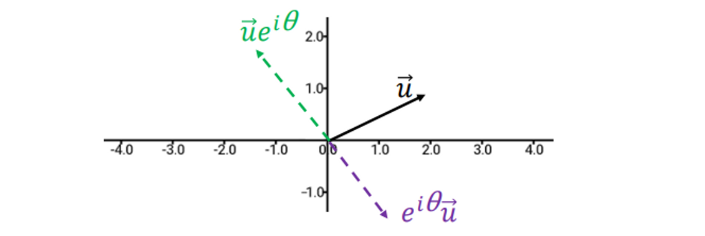
Geometric Product
- Geometric Product를 할 때
스칼라+bivector성립을 하지 않는데 어떻게 해야 하는가?
→ bivector 뒤에 i를 붙임
→ 실제로 밑에 보면 sin에 i 붙음
⇒ i를 붙임으로써 오일러 folmula를 이용해서 하나의 folmula로 바꾸는 것이 가능해진다
⇒ 스칼라 + bivector 가 polar form에서 exponential form 으로 바뀐다.
- u와 v가 nomalized vector면 ||u|| , ||v|| = 1이니 로 표현가능

- Conjugate of the geometric product
- Conjugate : 스칼라는 그대로 두고 i가 붙는 것에 부호를 바꿈
- ex)
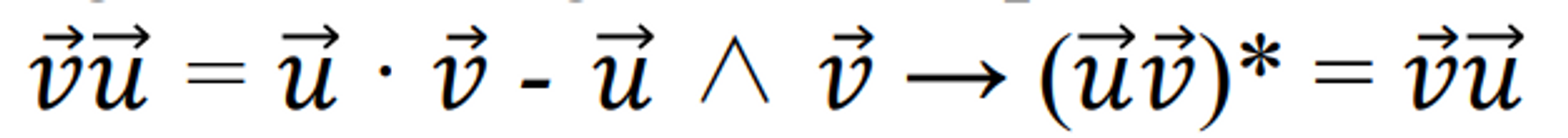
- 원래는 교환법칙이 성립이 되지 않지만 Conjugate 를 해주어서 앞뒤를 바꾸어 빼주는 것이 가능해진다. (아래 사진의 *이 conjugate이다. 지수 자리에 표시되어야 하는데 살짝 중간에 있어서 애매해 보인다..)
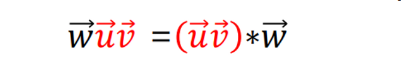
✔ Example
- θ만큼 회전하는 v
- w에다가 uv(회전을 표현하는 geometric product)를 적용해줌 → 뒤에 붙었기 때문에 CCW로 돌아가게 된다.
- uv자체가 회전표현이 된다.
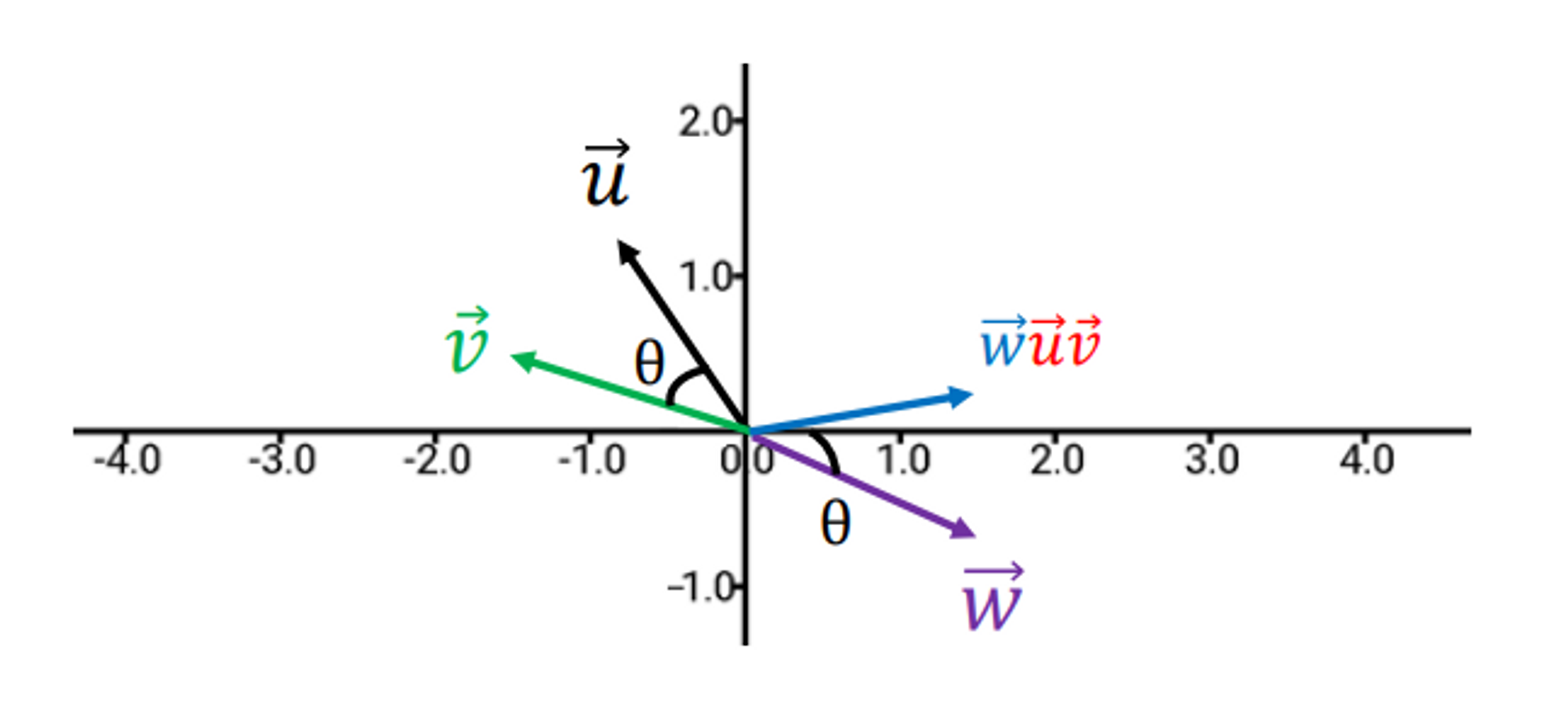
🧐 여기까지 정리
u에다가 벡터 y를 곱했을 뿐인데
- geometric product라는 포맷을 정의
→ 웻지 프로덕트, 두개 제곱했을 때 -1이 되고 이런걸 정의
- 이런 몇개의 정의를 하고 뒤에 psuedoscalar를 붙이니까 회전이 표현이 되었다.
- 그리고 웻지 프로덕트 bivector에 i를 붙여주고, 오일러 포뮬러에의해 θ를 포함하는 회전을 표현하는 식으로 바뀜
- 이것을 이용해 회전을 표현했더니 두개 이용해서 회전 곱해주는 것만으로도 벡터를 표현해주는 것이 가능해진다.
✔ 3D geometric algebra
In geometric algebra in 3-dimensions, a multi-vector has eight components
- 멀티벡터 2차원에서는 벡터 2개와 바이벡터로 표현이 되었다.
- 3차원은 component가 늘어나니 벡터 3개 바이벡터 3개 트라이벡터로 표현한다 → In geometric algebra in 3-dimensions
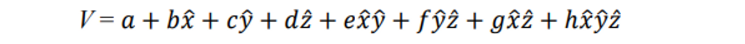
In 3D, the pseudoscalar
xyz가 i가 되어야 한다.
- x에다가 뒤에다가 i를 곱해본다. higest grade basis니까 xyz가 튀어나옴.
→ xx = 1이니 yz가 된다. ⇒ yz는 바이벡터
⇒ 2d에서는 u에다가 i를 곱하면 회전하는 벡터가 튀어나왔는데 쓰리디에서는 회전이 튀어나오게 된다.
- 임의의 벡터 v에다가 i를 곱하면 어떤 U라는 바이벡터가 나온다.
- -v는 Ui로 표현이 가능하다
→ vi = U에서 양변에 i를 곱한것
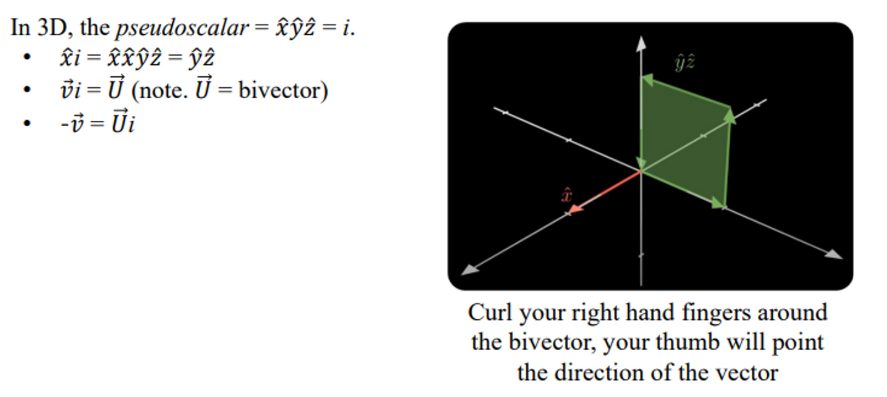
Therefore, a general 3D multi-vector can be rewritten as follows:
- bx + cy + dz → 결국 (b,c,d)이니 그냥 u벡터로 표현
- 바이벡터를 basis로하는 좀 회전한 것들고 그냥 → vi 로 표현
- 위의 식을 4개로 간단화한것
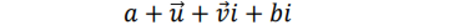
cross product
- 어떤 축을 기준으로 회전을 할 때 많이 사용
- 로터의 개념과 비슷함
- 두개 사이의 관계가 존재하는게 여기서 살펴볼 것임
Outer product and cross product
-
두개의 벡터 uv를 geomatric product를 한다.
→ 앞에 있는 것이 u · v , 뒤에 있는 것이 u ∧ v -
웻지 프로덕트는 뒤에 붙는 것이 rotor인데 크로스 프로덕트는 벡터이다.
-
x에다가 i를 곱하면 xi = xxyz = yz이다. 그래서 i를 곱하면 아래와 같은 결과가 나온다
⇒ 기존의 cross product를 이용해서 표현한 회전이 outer product를 이용해서 사용할 수 있는데 그냥 수도스칼라 붙이면 된다.!
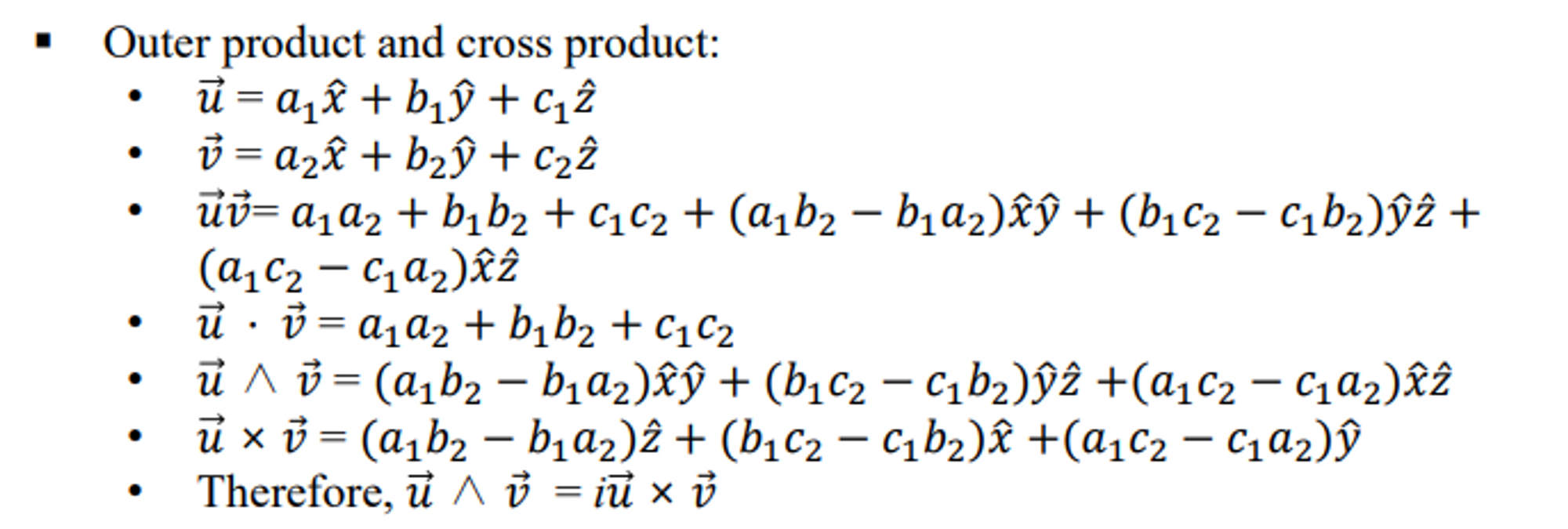
구체적으로 ~
- 벡터 v를 z-axis를 기준으로 90도 회전
- v = (3, 2, 1)
- v’ = (3, -2, 1)
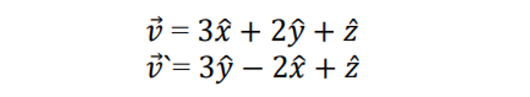
- 2d 회전에서 bivector를 기준으로 회전을 했다.
→ v 벡터 뒤에 xy(bivector)를 붙여 회전(CCW)
→ z가 아니고xyz라는 이상한 trivector가 나오게 된다.
→ 없애주려고 노력을 해본다
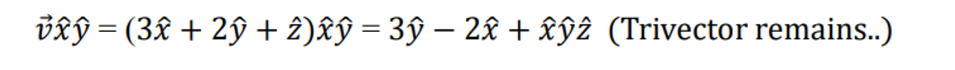
- conjugate 시켰더니 결과가 똑같아야하는데 예상과 다르게 된다.
→ 뒤에-zyx가 붙는다!
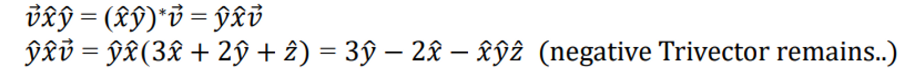
- 이번에는 앞 뒤에 다 붙여보자!
→ z는 나왔는데 앞에가 틀렸당.. 세타만큼 두 번 이동했으니 틀림
→ 그러면 앞에서 θ/2 , 뒤에 θ/2 붙이면 되지 않을가?
→ 근데 geometric product에서는 단순히 스칼라를 나누어 버리면 안된다 웻지 product에다가 나눠야한다.
⇒ 이전에 스칼라 + 웻지 프로덕트를 하나의 exponential 로 표현할 수 있었다. 이건 그냥 스칼라처럼 나누기 2 뭐 그렇게 사용했었다.
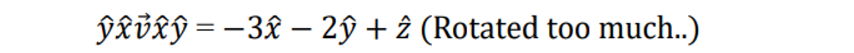
- 그렇게 했더니 우리가 원하는 v’이 나왔다
⇒ 3차원에서의 회전은 앞에서도 반만큼 뒤에서도 반만큼해서 움직여주어야 하는구나!
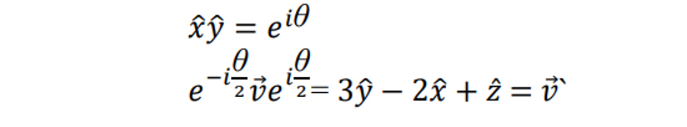
- vector v를 angle θ만큼 I라는 plain에서 옮길 때
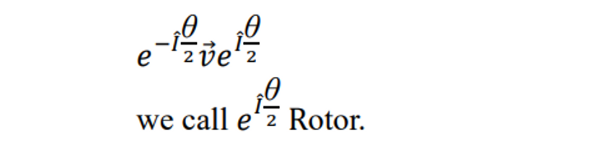
🖤 Quaternion 🖤
Rotor와 컨셉이 유사하다.
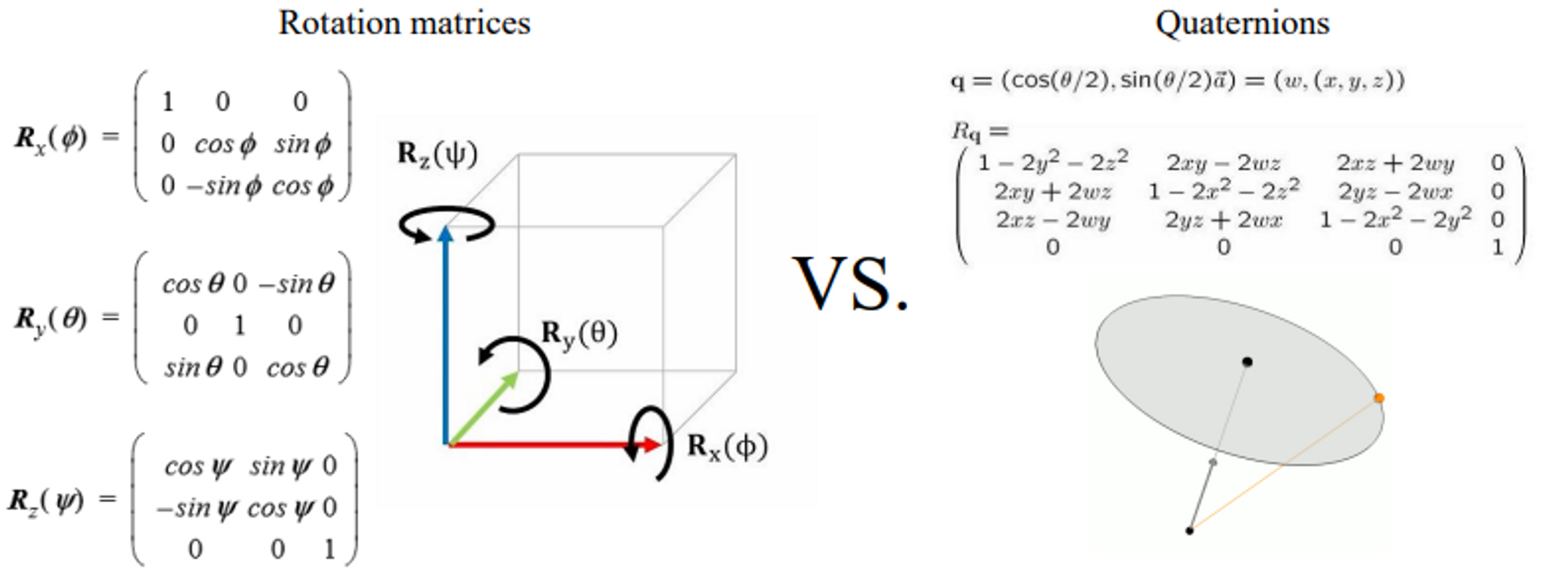
matrix을 이용한 회전의 문제점
보통 rotation을 표현할 때 rotation matrix를 이용해 많이 표현을 한다. rotation matrix 는 z, y, z축 기준 회전인데 이게 직관적이지가 않다. 회전을 정의하기 위해 x축으로는 얼마 회전해야하고, y축으로는 얼마 회전해야하고, … 3개의 축을 기준으로 하기 때문에 이를 모두 정의해주어야 한다.
→ 축 회전은 continuous한 영역에서는 큰 문제가 되지 않는다. 그러나 discrete한 영역으로 보내면 특정 timestamp로 00초 이후의 회전을 나타내는 것인데 각 축들이 원래는 전부 interpolation을 통해 스무스하게 움직여야 하는데 discrete하다 보니 어떨때는 x축 회전이 좀 더 많고 이런 상황이 발생한다. 특히 게임에서 timestamp를 적게 쓰면 cost가 크고 보통 60fps로 고정을 하는데 그러면 회전에서 지글지글함이 보인다.
⇒ 이를 해결하기 위해 Quaternion이나 Rotor을 이용한 회전을 정의하게 된다.
Quaternion 이란?
⇒ 임의의 축을 기준으로 회전을 정의할 수 있는 것
- 3차원 공간 상에서 회전을 컴팩트 하게 나타내는 것
→ 3차원에서만 사용한다. 다른 새로운 축이 등장하면 이것을 이용한 회전을 표현할 수 없어 Rotor를 사용
- 특정 축을 기준으로 회전을 표현하는 것
- rotation matrices에 비해 compact, efficient, and numerically stable(발산x)
- 하지만 not intuitive and easy to understand
- In a 3-dimensional space, according to Euler’s rotation theorem
→ 어떤 rotation이든 고정된 point에 대한 rigi d body rotation은 고정된 축을 기준으로 몇 도 회전하는 것으로 모두 표현할 수 있다. - Quaternions는 axis-angle representation으로 바꾸어 준다. 임의의 축을 기준으로 몇 도 회전하냐?
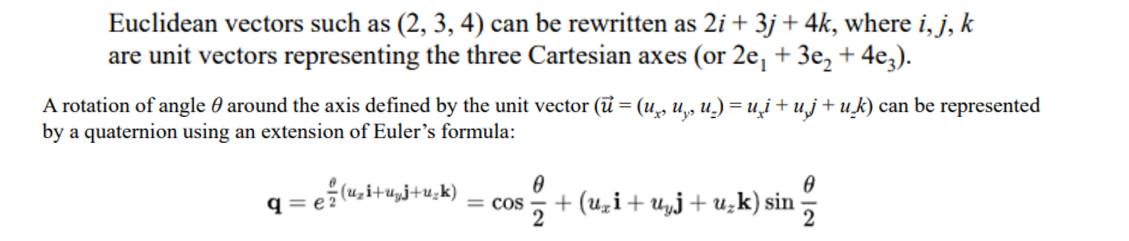
⇒rotor에서 많이 봄 폼이다. rotor에서 I가 어떤 축을 기준으로 회전할거냐에 대한 unit vector였다.
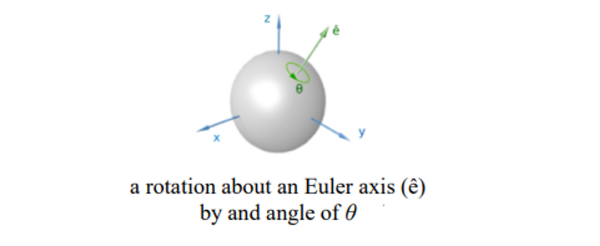
- 실제로 회전을 할 때 아래와 같이 표현한다.
→ 회전하려는 벡터에 앞뒤로 붙이는게 rotor와 유사

-
matrix rotation을 바꾸려는 이유는 연산이 빨라지기 때문이다
-
Rotor는 Quaternion을 조금 더 generation하게 표현하는 것.
🖇 Reference
해당 포스트는 강형엽 교수님의 게임공학[GE-23-1] 수업을 수강하고 정리한 내용입니다.
