[Computer Vision] LoG, Template Matching and Corner

SYiee·2023년 11월 8일

목록 보기

6/11

💡 What we learn last session?

Edge Detection

우리는 이미지에서 edge를 찾고자 했다. 특징을 찾기 위해서이다. 그래서 gradient를 구했고 여기서 극값을 찾고자 threshold를 정해 edge를 detection했다. 하지만 edge가 두꺼우면 안되게 때문에 thinning이 필요했고 threshold를 조정하거나 2개 이상 사용하였다.

📌 Second-Derivative Filters

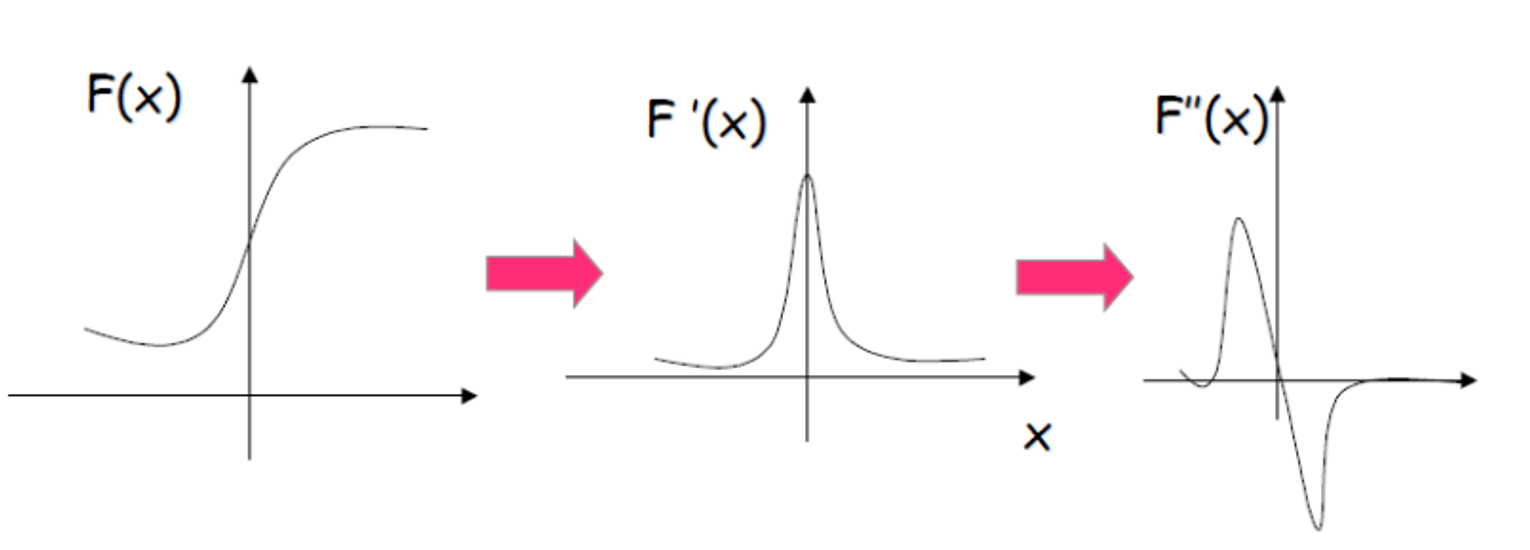
edge detection을 위해 우리는 1차 미분을 했다. 여기서 극댓값을 찾기 위해 threshold를 설정했었다. 그런데 극댓값은 $F''(x) = 0$ 이 되는 x를 찾으면 손쉽게 edge를 찾을 수 있다.

$F'(x)$

장점

미분을 한 번만 하면 된다.

단점

threshold를 정해야 한다.
edge가 뚱뚱해진다.

$F’(x)$

장점

threshold를 찾을 필요가 없다
edge가 thick해지지 않으니 thinning을 할 필요가 없다.

단점

Noise에 취약해진다 원래 미분하면 noise가 더 생긴다. 근데 두번 하면 더 심해진다..

🤔 그렇다면 noise를 없애기 위해 그냥 smoothing을 세게 하고 gradient 하면 안 될까? smoothing을 시키면 noise가 줄어드니 말이다.

🔥 Remaining problems 🔥

미분이 쉽지 않다.

그런데 문제는 미분이 쉽지 않다는 것이다. discrete한 값을 사용하기 때문이다. 앞서도 이야기 했지만 미분은 한다는 것이 그렇게 쉽지가 않다. 그렇기에 우리는 filter를 사용할 것이다.
원치 않는 data를 얻을 수도 있다.

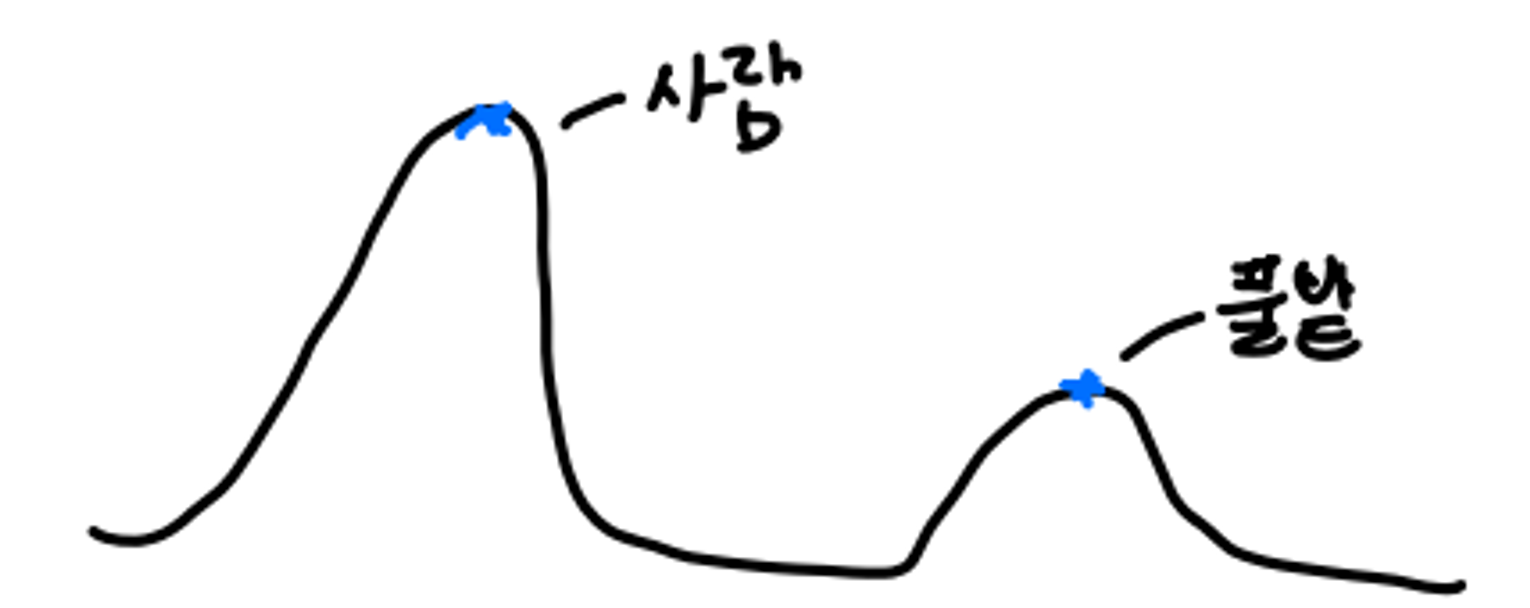
아래 사진과 같은 data가 있을 때 우리는 사람에 해당하는 edge만 detection하고 싶다. 그러나 두 번 미분하면 다 사람과 풀밭에 대한 정보를 둘 다 얻게된다. 이전에 미분을 한 번만 $F'(x)$ 만 할 때는 threshold를 설정하면 풀밭처럼 극값이지만 threshold보다 낮은 값들을 자연스럽ㄱ 걸러졌다.

하지만 두번 미분하는 방법을 사용하면 threshold의 부재로 인해 문이 개방되면서 모든 극값들이 들어와버린다.

→ 그래서 보통 사용을 할 때는 general threshold를 잡고 미분을 두번하는 방식으로 사용한다.

✔ Numerical Derivatives

Taylor Series 를 이용한다.

우리에게 주어진 값 given data는 $f(x+h), f(x)$ 이다. image 의 signal값이다. 우리가 구하고자 하는 값은 $f''(x)$ 로 이차 미분값이다.

아래 두 식을 더하는 과정에서 일차 미분과 삼차 미분값은 자연스럽게 사라지게 된다. 그러나 나머지 값들 $O(h^4)$ 은 Error로 남는다.

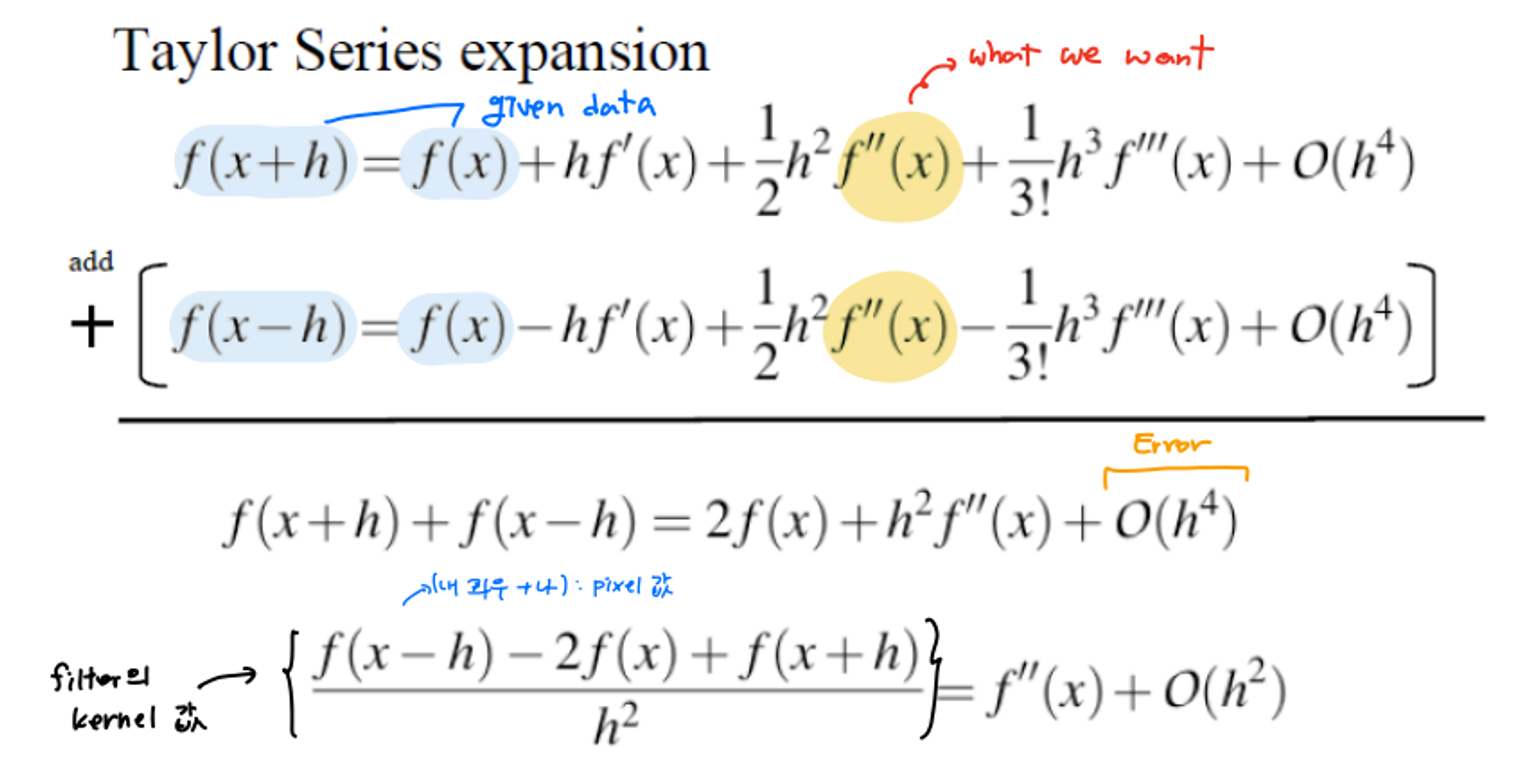
최종으로 나온 식을 보면 좌변에 해당하는 값이 filter의 kernel 값이다.

$f(x-h) -2f(x) + f(x+h)$ 을 보면 나(x)의 픽셀 값과 좌우 픽셀값(x-h, x+h)를 사용하는 것을 알 수 있다.

✔ Example

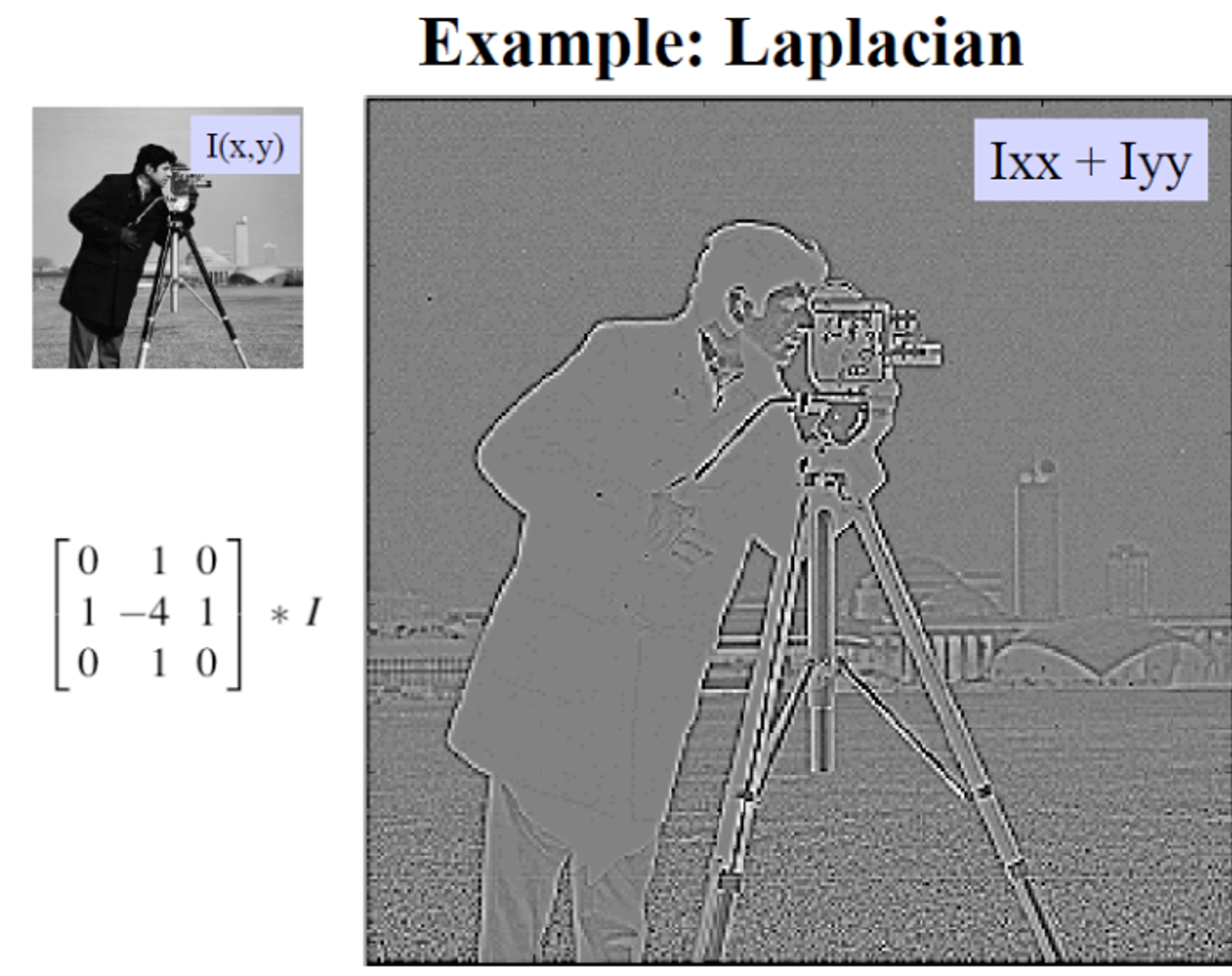
아래 사진을 보면 원본 이미지에 2차 미분 필터를 적용했더니 오른쪽과 같은 결과값이 나온 것을 알 수 있다.

128인 값( $f''(x= 0)$ 은 절대 나오지가 않는다. discrete한 data이기 때문이다.

→ 대신 우린 crossing 하는 곳을 찾는다. 예를 들어 내 왼쪽값은 128보다 크고 오른쪽은 128보다는 작은 값을 갖는 crossing하는 곳을 찾는다.

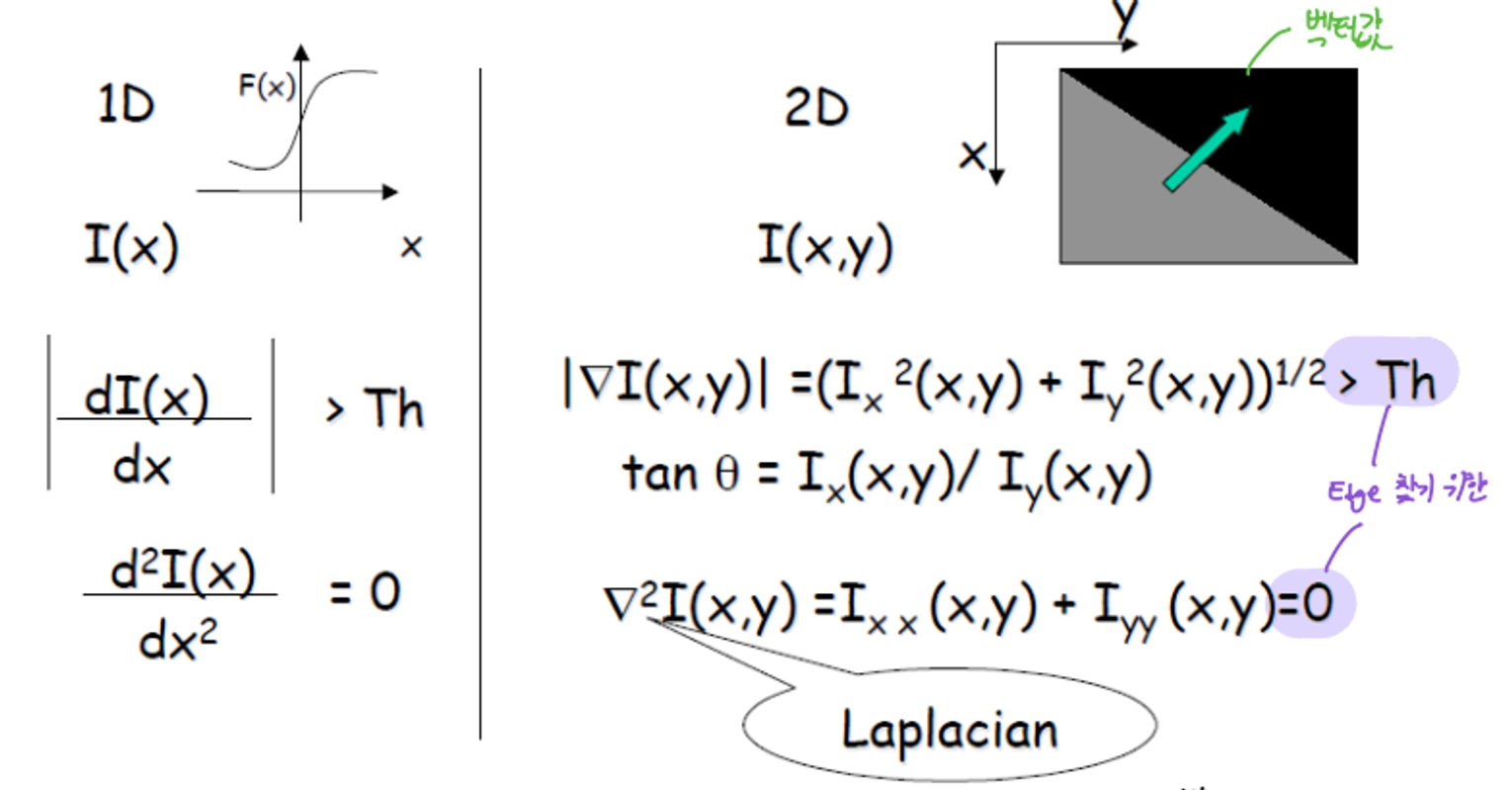
📌 Edge Detection (1D to 2D) & LoG

1D

input image signal : $I(x)$
$I'(x) > threshold$
$I''(x) = 0$

2D

input image signal : $I(x,y)$
$∇I(x,y) > threshold$
$∇^2I(x,y) = 0$

→ 이때 $∇^2$ 를 x와 y 방향으로 두 번 미분한 것으로 Laplacian이라고 부른다.

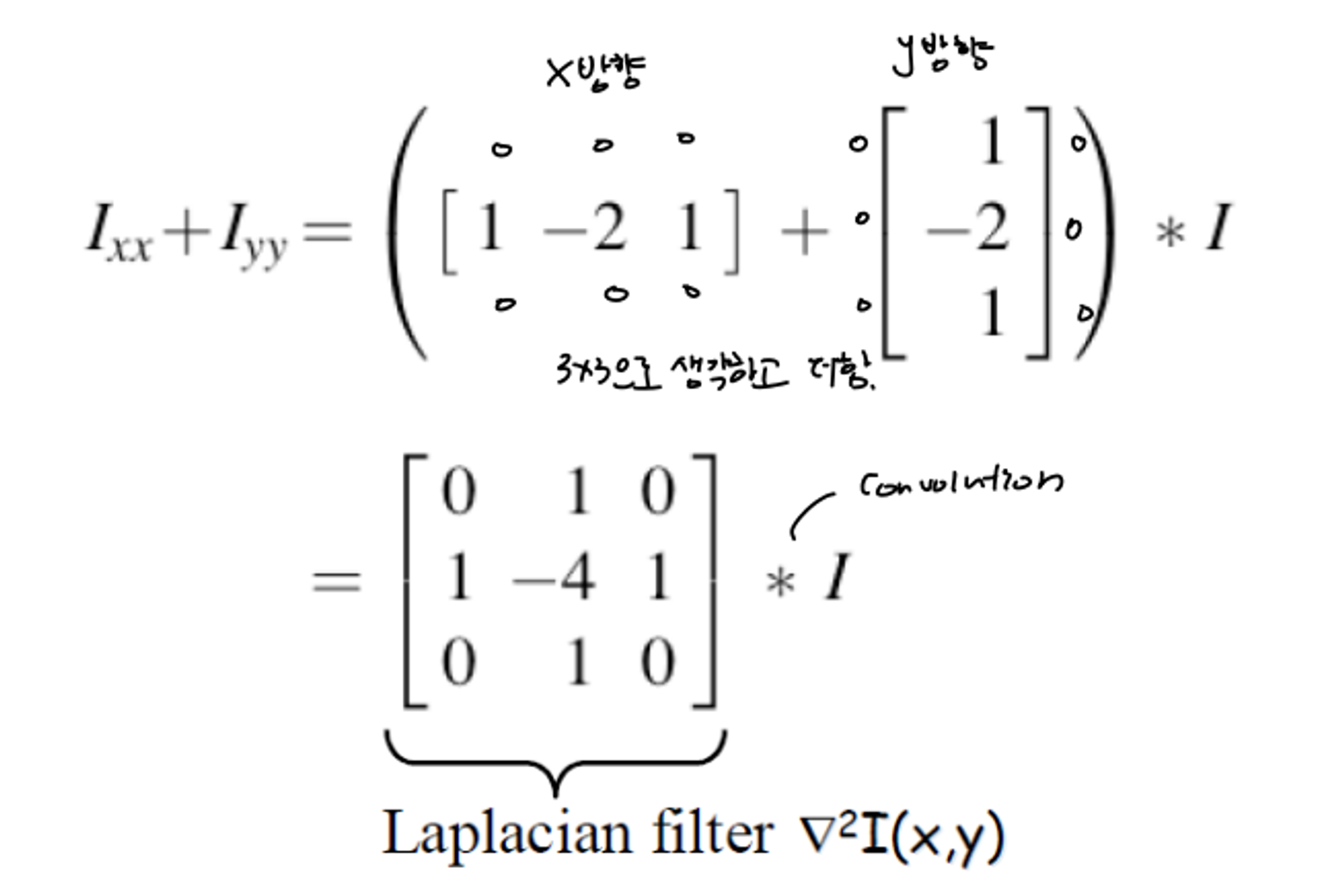
✔ Finite Difference Laplacian

x방향과 y방향의 second derivative filter를 더한 값이 Laplacian filter가 된다.

그 후 image signal과 convolution을 한다.

📍 Notes about Laplacian

$∇^2I(x,y)$ : scalar
- 스칼라 값이기 때문에 orientation 정보가 사라진다.
- 2차 미분의 합이다. → 미분을 두 번 하여 noise가 올라간다. noise에 민감해지게 된다.

⇒ smoothing filter와 결합하여 사용해야 한다.

아래 사진처럼 이미지에 smoothing filter를 먼저 통과 시키고 Laplacian filter를 적용시키는 것을 상상하겠지만 실제로는 1→2 순서로 이루어지지 않는다.

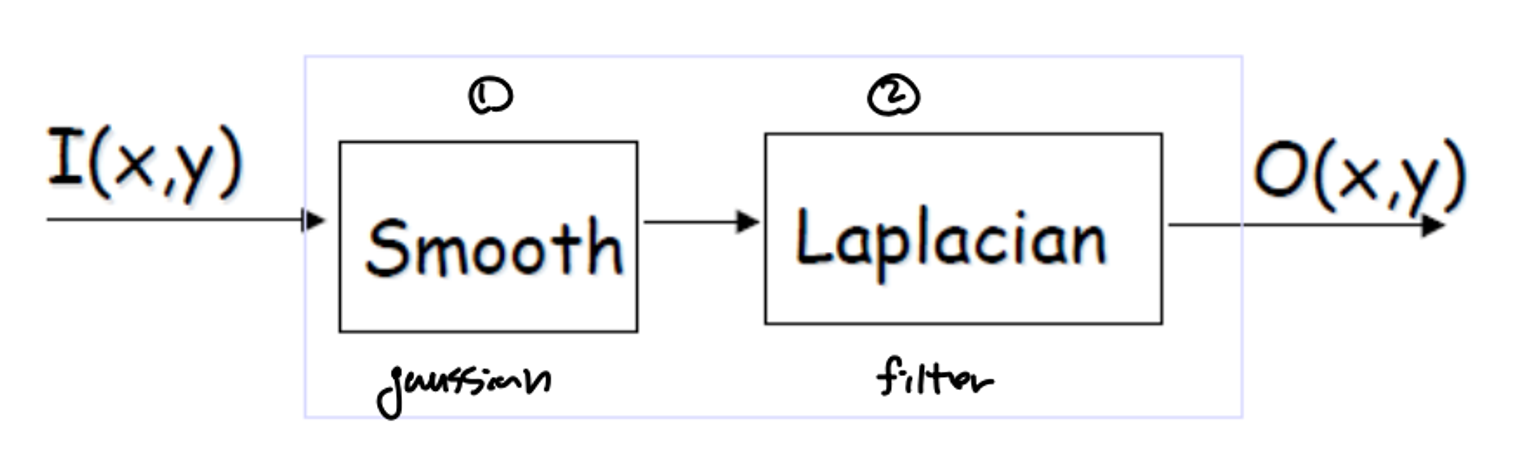
우리는 이전에 앞에서 convolution의 특성에 대해 배웠다. Convolution은 Commutative한 성질을 가졌다. 이것을 이용해 계산을 해보고자 하낟.

✅ LoG(Laplacian of Gaussian Filter)

What we want to do?

To detect the edge → why we have to detect edge? → cause edges have some properties which is different from neighbors.

Image → Gaussian smoothing → Laplacian

Simply → LoG is a Laplacian filter which is added smoothing

✔ Original method : Gaussian smoothing to image → Laplacian filter

이 방법을 사용하면 convolution을 더 많이 하게 된다.

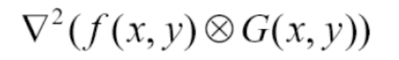
✔ Better Way : Laplacian filter to Gaussian smoothing → convolution with image

이 방법을 사용하면 convolution 수를 줄여 훨씬 빠른 계산이 가능해진다.

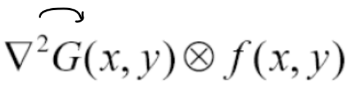
📍 1D Gaussian and Derivatives

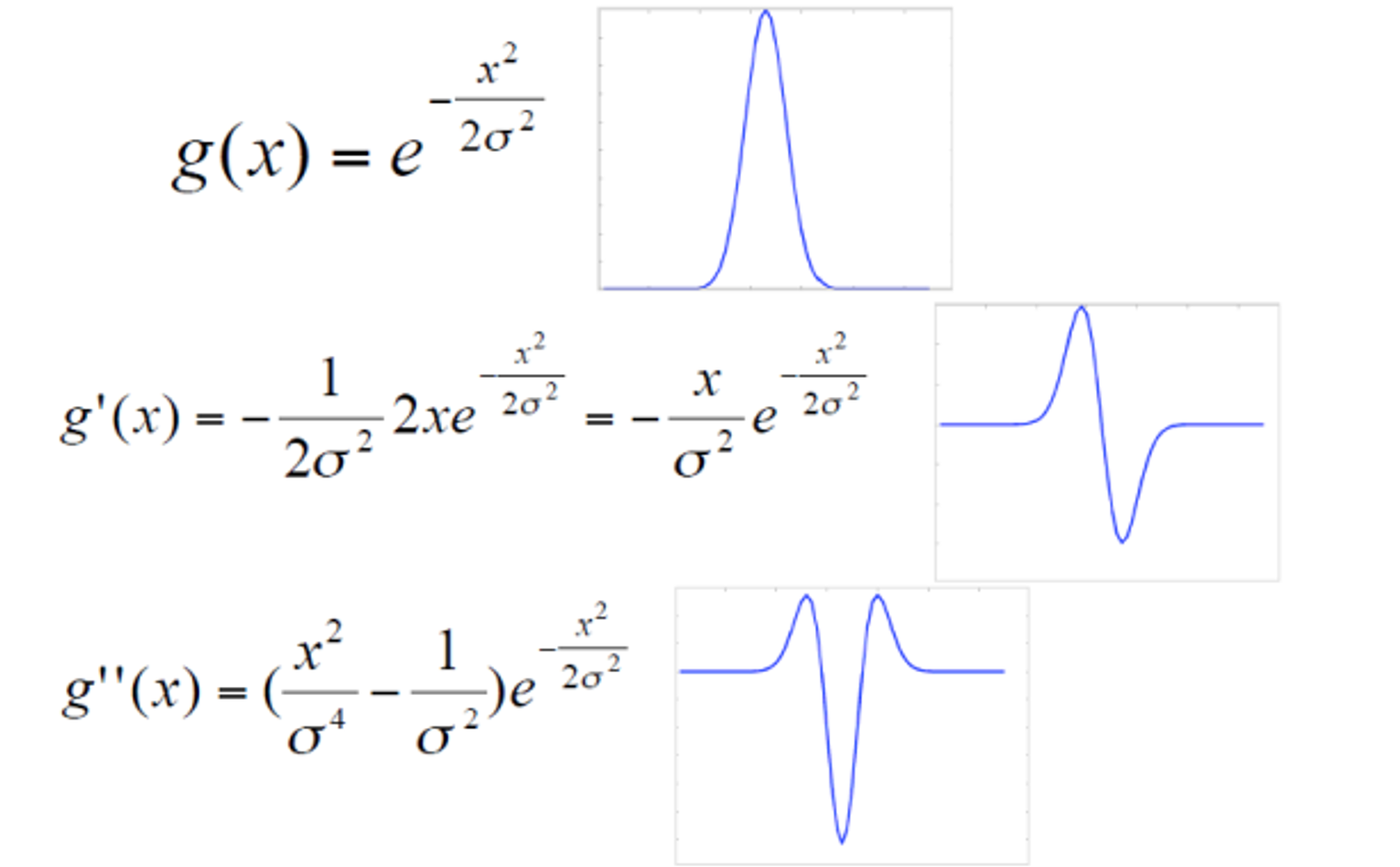
📍 Second Derivative of a Gaussian

위의 1D의 가우시안의 2차 미분을 2D로 가져오면

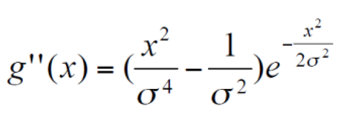
아래 사진과 같다. 입체 꼬깔이 되었다.

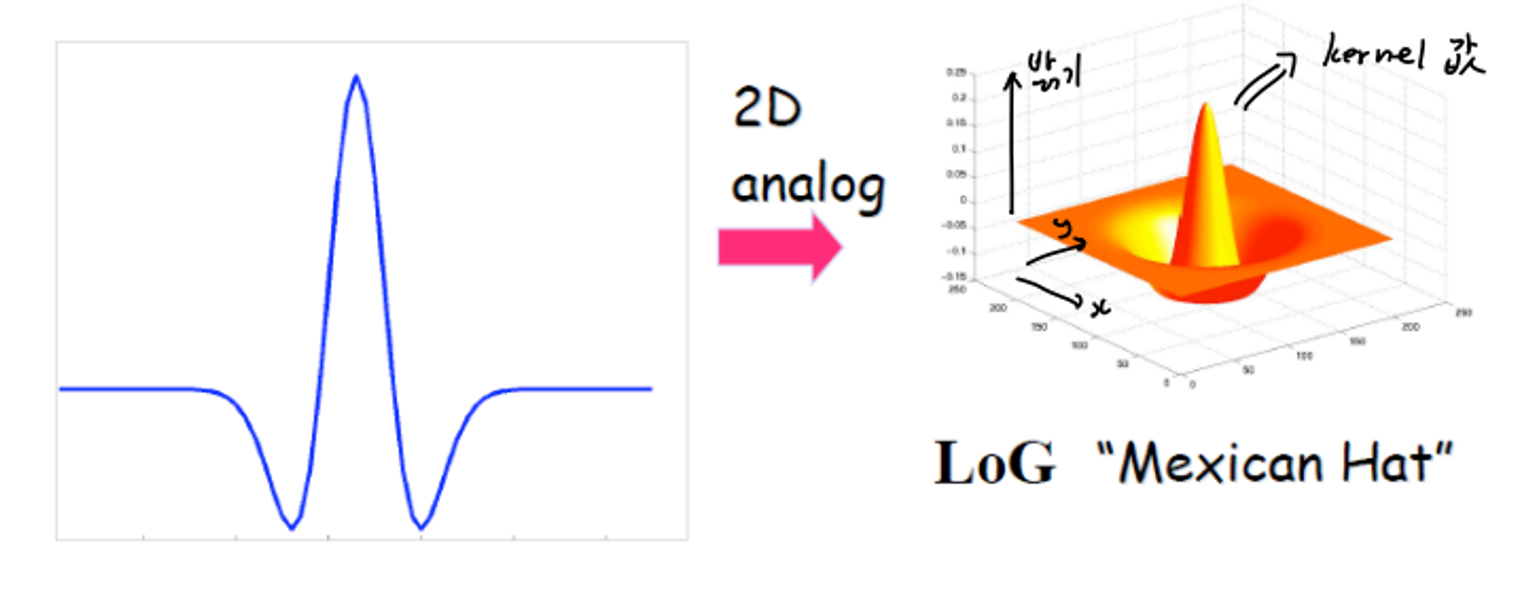
Effect of LoG Operator

Band-Pass Filter

low frequency와 high frequency를 모두 살릴 수 있다

✅DoG ( Difference of two Gaussian )

위에서 구한 Laplacian이 두개의 Gaussian의 차와 유사하다.

유의해야하는 것이 Derivative of Gaussian도 DoG라고 불리니 용어를 헷갈리지 않도록 조심하자.

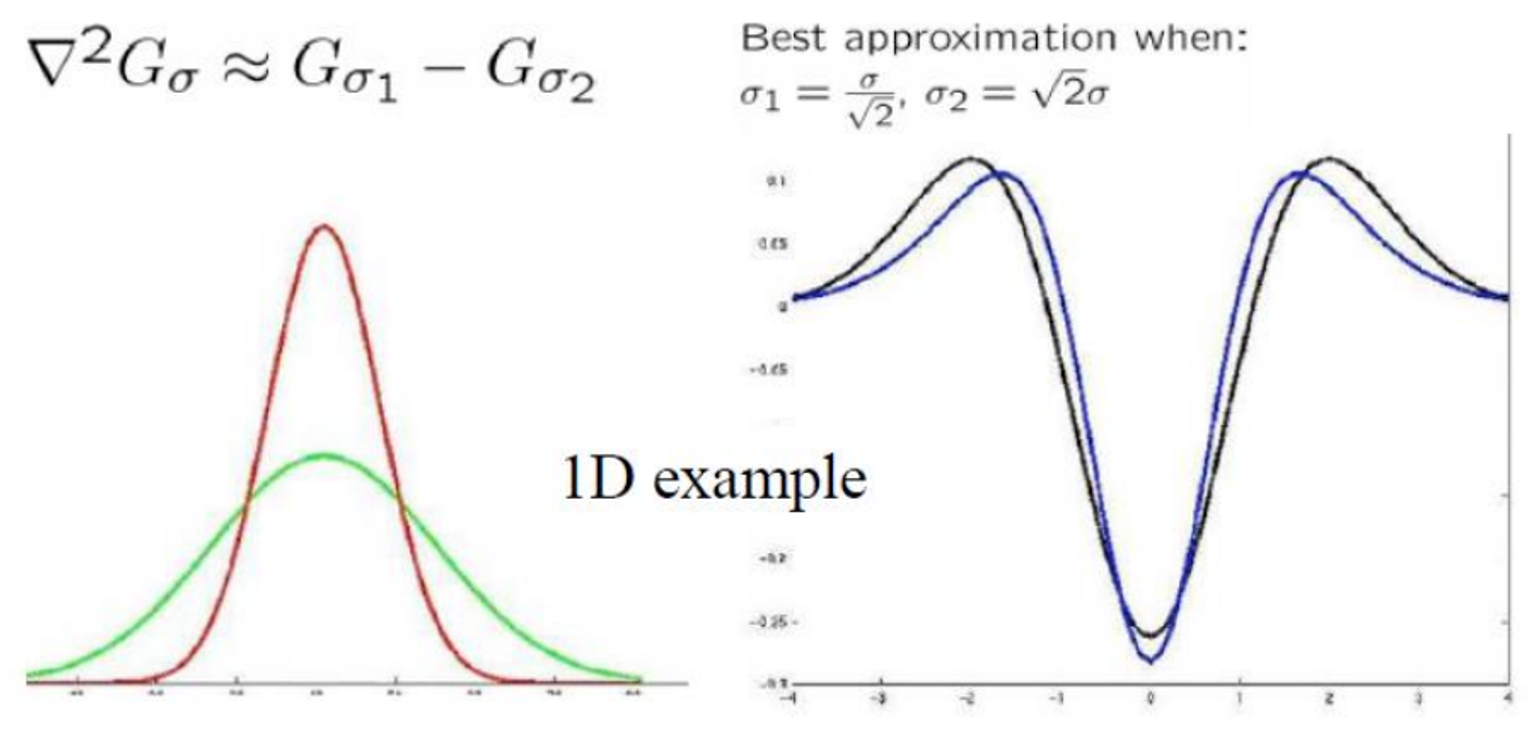
LoG는 DoG를 이용해 손쉽게 approximation이 가능하다.

✔ Example : LoG Extrema

sigma 값이 커질 수록 뭉뚝해진다

그런데 사진을 보면 isolated된 영역 Blob이 생긴 것을 볼 수 있다.

우리가 이전부터 해왔던 filtering을 하는 작업은 모두 Convolution으로 이미지에서 kernel 모양과 비슷한 것을 찾는 것이다. 근데 가우시안의 이차미분 그림을 보면 볼록 튀어나온 부분이 마치 Blob처럼 보이는 것을 알 수 있다.

우리는 여기서 인사이트를 얻어 이 가우시안 필터를 blob detector로 사용할 수도 있다는 것을 알게 된다.

✔ LoG Blob Finding

⚡ LoG filter extrema locates blobs

maxima = dark blobs on light background
minima = light blobs on dark background

⚡ Scale of Blob

LoG filter 의 sigma parameter 값( standard distribution )을 조정하여 blob의 사이즈를 조정할 수 있다.

아래 사진의 예시를 보면 sigma가 2일 때는 사람의 눈 정도를 감지할 수 있었는데 sigma가 10이 되면 blob의 사이즈가 커져 사람의 머리를 감지할 수 있게 된다. 이를 통해 feature detection 이 가능해진다!

💡 Observe and Generalize

♻️ Review till here

다시 처음으로 돌아가 보자.

앞서 우리는 edge를 detection 하고 싶었다. 이에 이차 미분을 하는 Laplacian filter 을 사용했다. 그러나 미분을 두 번 하면서 noise가 많아졌다. 이에 noise를 줄이기 위해 Gaussian filter를 사용해 먼저 smoothing을 했다. 이를 LoG라 불렀다.

그런데 LoG를 한 결과들을 가만히 들여다 보니 특정 부분이 동그랗게 어둡거나 밝은 부분을 발견했다. 바로 Blob이다. 이제 이런 Blob을 사용해서 이미지에서 특징을 찾아내보고자 한다. 그리고 이를 generalize해보자.

Key Idea

앞서 convolution 한다는 것이 filter와 비슷한 모양인지를 찾는 것이라고 했다. 그렇다면 Gaussian filter만이 아니라 다른 사진과도 비교가 가능할지 않을까? 라는 생각에서 generalization을 시작한다. 내 얼굴을 kernel로 써볼까?

Template Matching

아래와 같은 사진을 kernel로 사용해보면 어떨까?

창틀에 해당하는 십자가를 이미지랑 convolution하면 맨 오른쪽과 같은 결과가 나오게 된다. 그런데 맨 오른쪽에 있는 사진을 보면 원래 이미지를 뽑은 곳은 밝게 표현이 되는데 가장자리로 갈수록 어두워지는 것을 볼 수 있다.

위에서 언급한 것처럼 완전 동일할 때는 큰 값, 조금씩 다르면 작은 값을 갖는다.

그런데 측면에서 본 사진으로는 정면에 모습을 찾기 어렵다. 그러나 우리는 이제 측면에서 본 사진으로도 정면의 모습도 찾고 싶다. 즉 측면의 kernel로 정면에서 본 것을 찾고 싶으니 우리는 element의 independent, robust한 특징을 찾고 싶다.

robust : 변화는 있지만 감당할 수 있는 정도
independent : independent feature

📌 Corner Detection

✔ What is corners?

코너는 특징을 갖는 특정 영역이다.

다른 시점에서 봐도 코너는 코너이기에 물체의 형상, 특징을 characterization 하기에 좋다.

edge나 boundary가 보면 edge 방향으로 쭉 이동하면 알 수가 없다. 그러나 corner는 어떤 방향으로 움직여도 알 수 있다.

Motivation for Corner Finding

corner는 key point, feature point이다. → 즉, 시점이 달라져도 견디는 포인트이다.
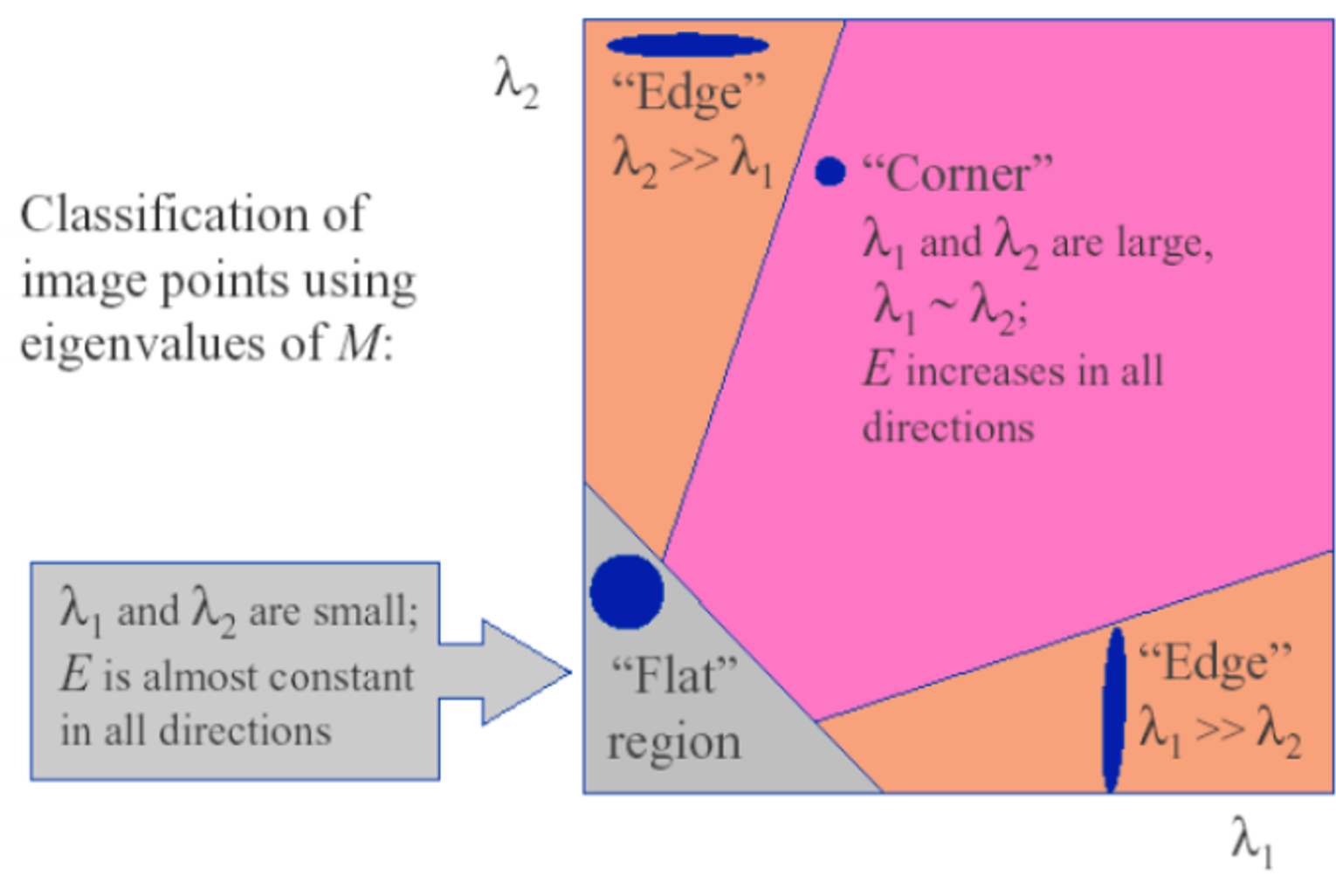
Eigen value
- if) 두 eigen value 값이 크다 ⇒ corner일 확률이 높다
- else) 두 eigen value 값이 거의 작다. ⇒ flat

✅ Harris Corner Detector

✔ Basic idea

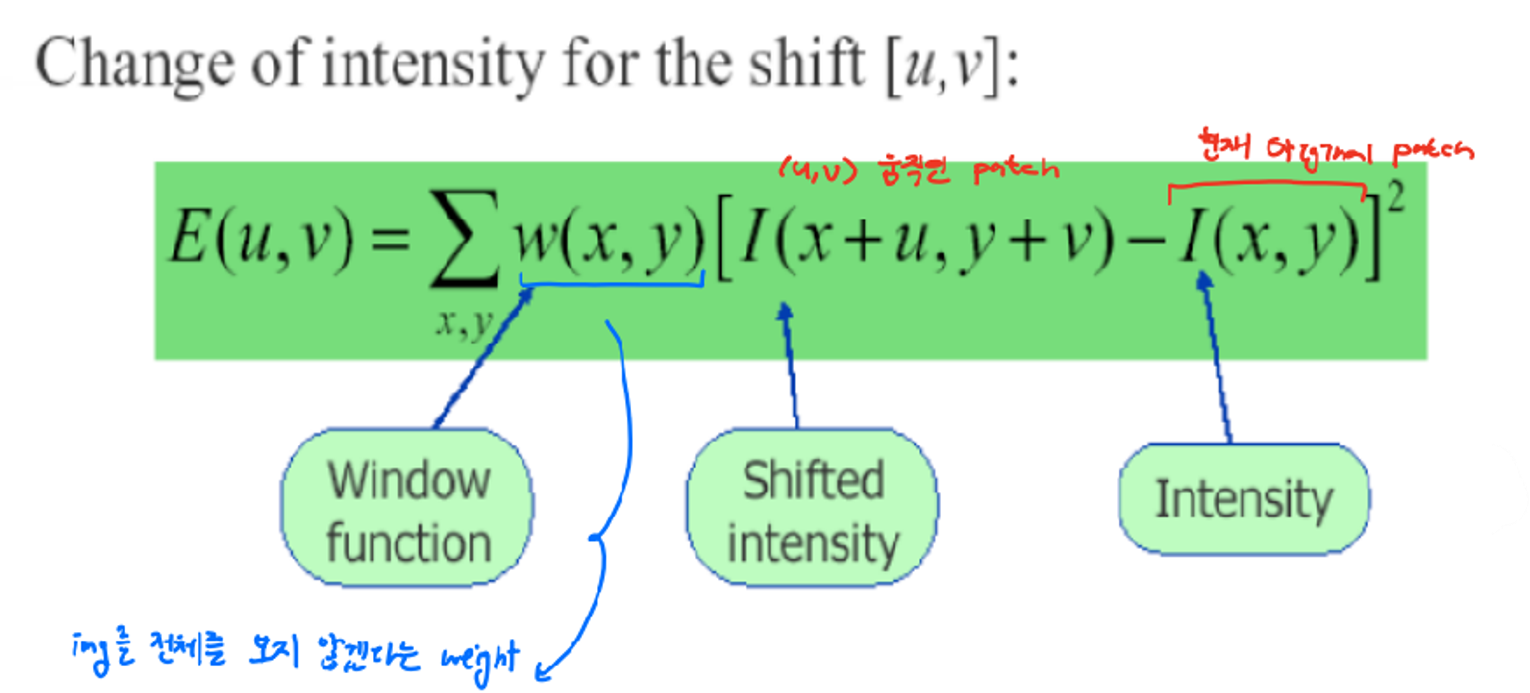
이미지의 한 픽셀의 중심점으로 잡고 그 중심 픽셀에 window를 설정해 window 내의 픽셀값의 합을 $I(x,y)$ 로 설정한다. 그 후 window를 x축 방향으로 u만큼 y축 방향으로 v만큼 이동시켜 다시 $I(x+u, y+v)$ 를 구해준다.

patch를 통해 현재와 움직였을 때의 유사도를 분석한다.

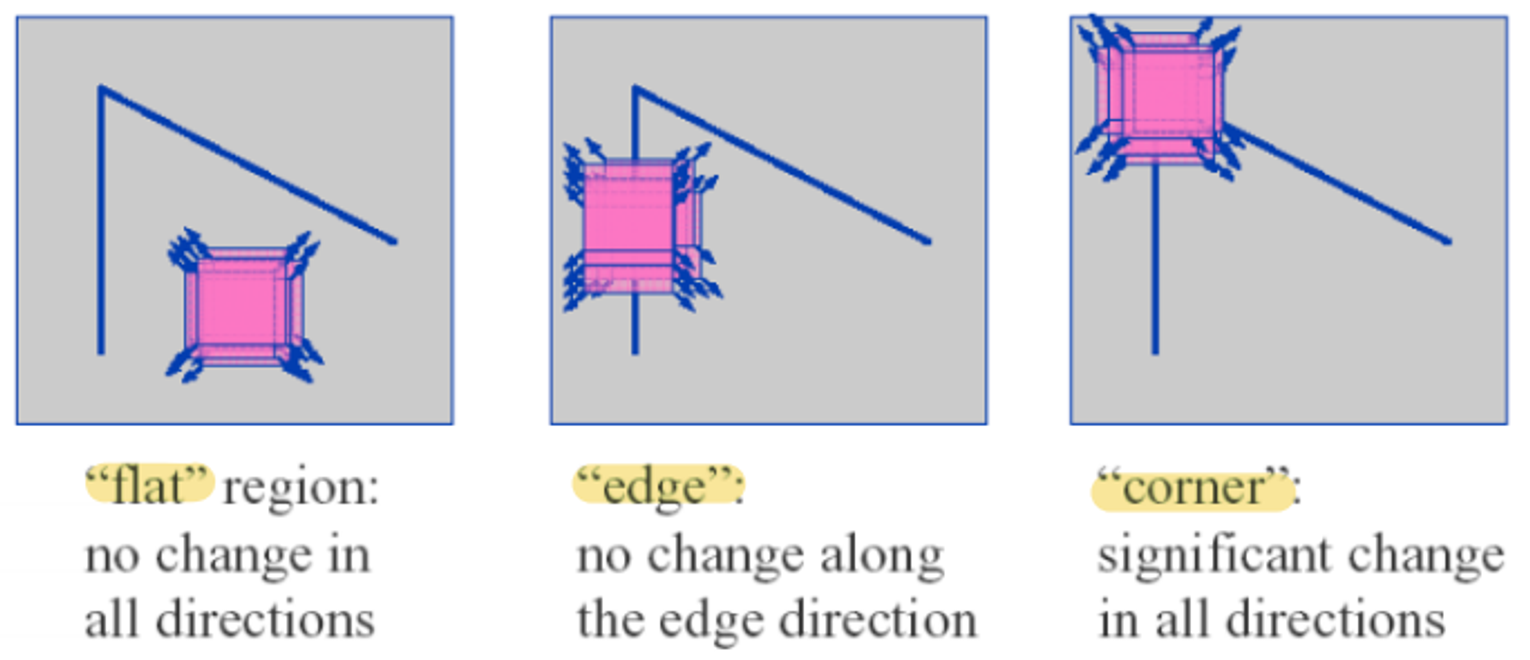
patch를 왔다갔다 하면 변화 가 3가지로 나타난다. 변화를

모를 때 → flat (픽셀 값의 어느 방향으로도 변화가 없다)
알 때 → edge (픽셀 값이 한 방향으로만 변화가 있다.)
방향에 따라 다를 때 → corner (픽셀 값이 모든 방향으로 변화가 있다.)

✔ Harris Detector : Mathematics

$I(x,y)$ : 현재 original patch
$I(x+u,y+v)$ : (u,v)만큼 움직인 patch
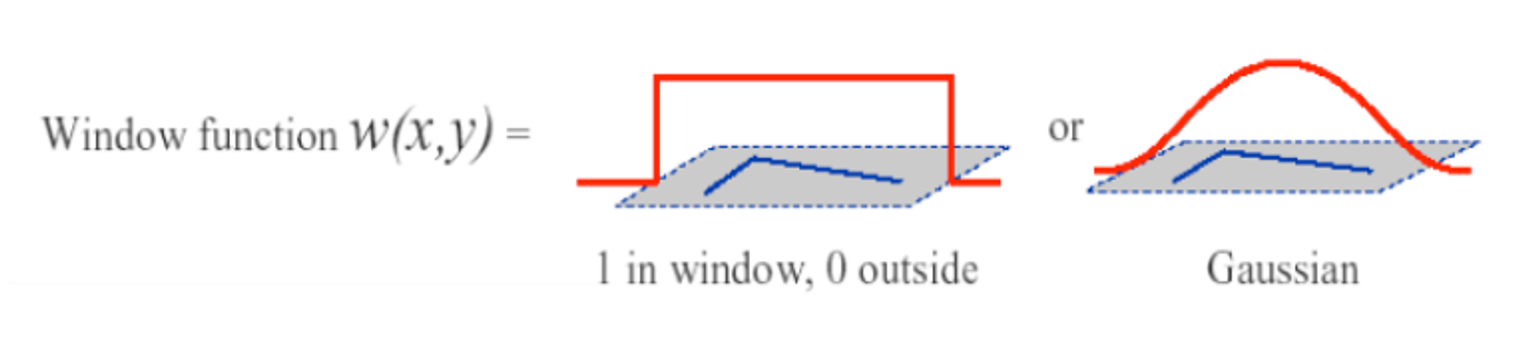
$w(x,y)$ : window function
→ img 전체를 보지 않게 하기 위한 weight

⇒ 현재의 patch와 움직인 patch의 difference를 구해서 corner인지 detect한다.

output == 0 : 두 patch가 같다. 유사하다
output이 크다 : 유사하지 않다.
⇒ Dissimilarity

⇒ 즉 E(두 값의 차이)가 크면 corner point이다.

📕 Dissimilarity vs Similarity

*Dissimilarity : 값이 높을 수록 다르다*

Similarity : 값이 낮을수록 같다

💨 Window function

✔ Taylor Series for 2D Functions

계산량을 줄이기 위해 patch를 shift해서 얻었어야 할 값을 original 값을 통해 예측하자.

✔ Harris Corner Derivation

위에서 예측한 shift된 patch 값을 통해 Difference를 구하는 식에 넣으면 아래와 가이 추정이 가능하다.

이를 matrix equation으로 정리한다. 시그마가 갖는 변수 값은 x,y 임으로 u,v 를 빼내면 최종적으로 맨 밑의 식이 나온다.

이제 이 식에서 우리는 shift 값인 **u, v** 말고 matrix M 의 특성을 파악해보고자 한다.

앞서 결과로 나오는 E (두 패치 값의 차이) 값이 크면 corner point라고 했는데 값이 크기 위해서는 아래에서 구한 matrix M 값이 커야 한다.

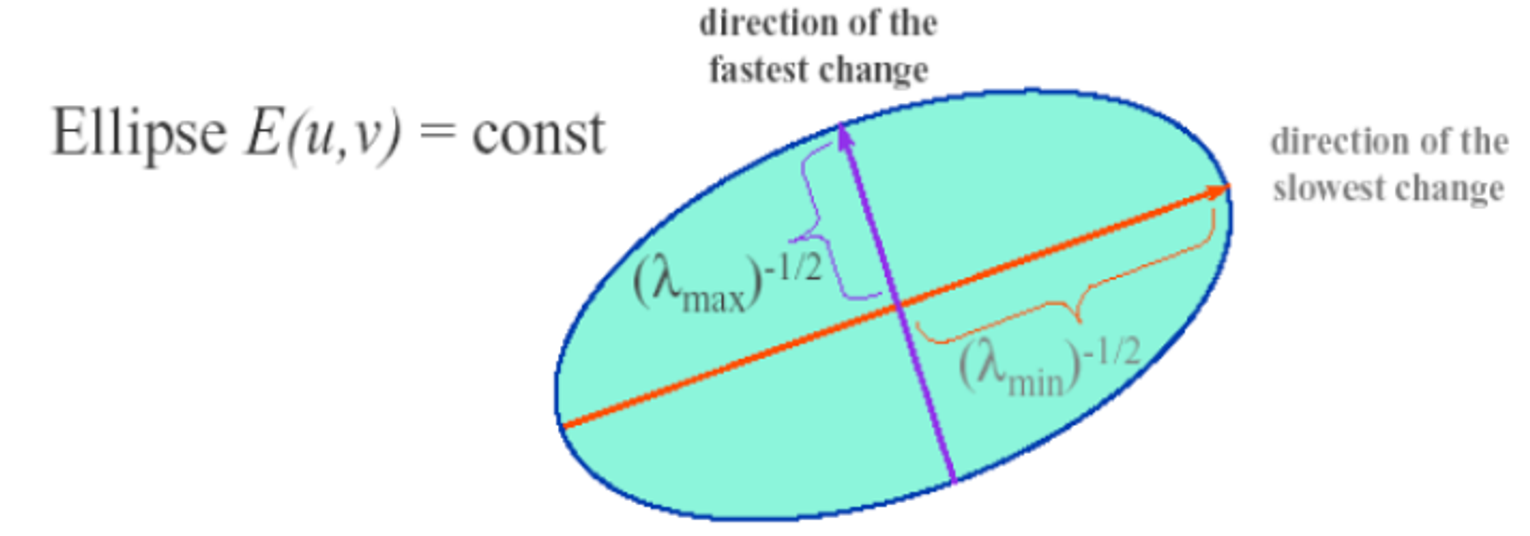
행렬을 고유값 분해하면 x, y 축 중 어느 방향으로 이미지 변화가 큰지 알 수 있다.

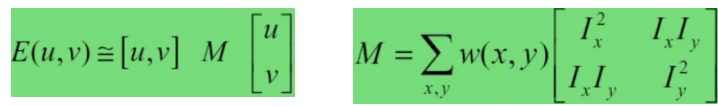
🗨 $**λ_1, λ_2$ : eigen value**

→ 고유값은 주어진 방향으로 얼마나 빠르게 변화가 나타나는지 특정한다

유의미한 값을 가지는 Full rank → eigen value가 의미있는 값이라 추정 가능
⇒ 유의미한 값이란 무엇일까?
- 만약 두 eigen value 값이 작다면 아래 사진처럼 거의 직선에 해당한다. 이는 determinant와 inverse를 구할 수는 있지만 eigen value로서의 의미가 없다고 볼 수 있다. 정보가 하나 있는것과 다름이 없다.
- 그러나 eigen value가 둘 다 큰 값이라면 서로 되게 다른 식이라는 것을 뜻한다. 그렇게 되면 의미가 있고 정보가 2개 있다고 할 수 있다.