📌 Gaussian Smoothing Filter
✔ Box filter vs Gaussian filter
우리는 이전 포스트에서 두개의 필터에 대해 학습했다.
box filter를 사용하면 원본에는 없는 흐릿한 선들이 생기기도 하는데 이를 ghost line이라 불렀다. 이는 box filter의 모양 때문이었다. 이를 보안하기 위해 적용한 것이 Gaussian filter이었다. Gaussian은 중심의 가장 큰 값이고 주변으로 퍼져나갈수록 값이 작아진다. 즉 중심에 더 많은 weight를 주고 거리가 멀어질 수록 weight가 감소하는 kernel인 것이다.

✔ Gaussian smoothing
standard deviation(표준편차) 가 클수록
→ 내 자리의 값을 구하기 위해 더 멀리있는 값까지 가져오게 된다.
→ 내 값이 많이 희석된다.
→ smoothing 효과가 커진다.
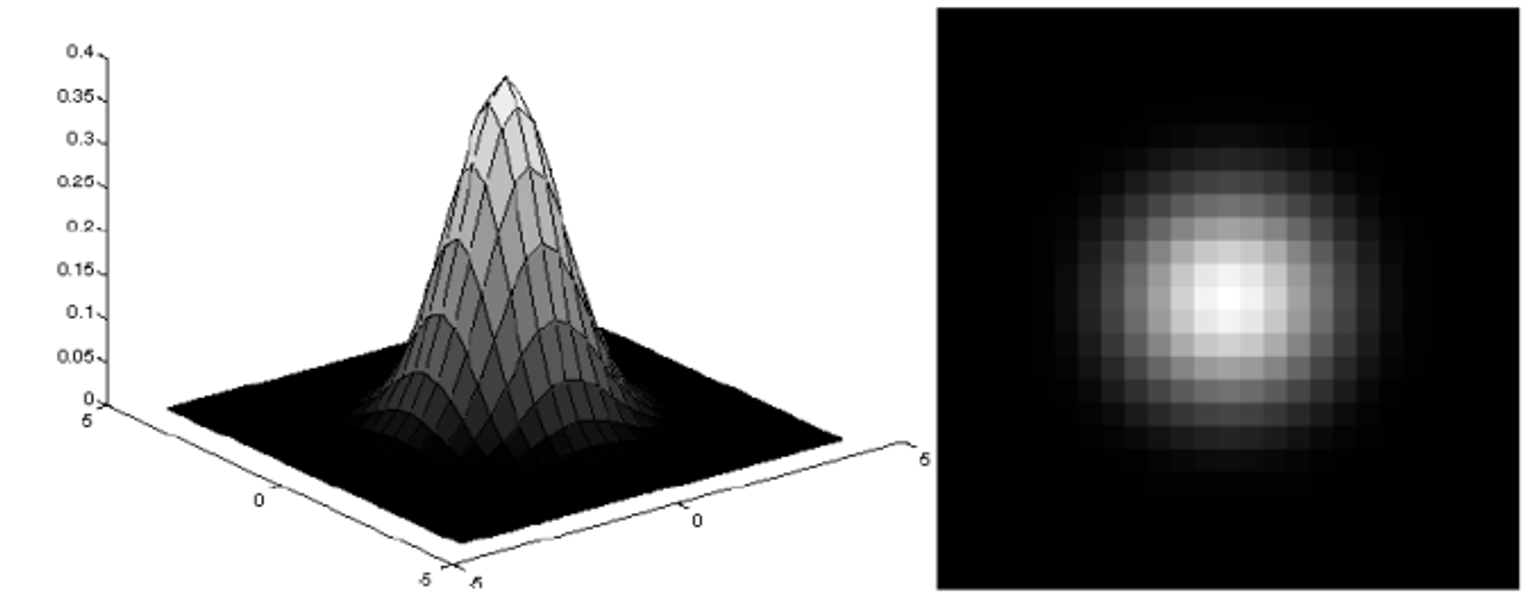
왼쪽은 분산이 1인 정규분포이고 오른족은 분산이 3인 정규분포이다. 솟아 오른 부분이 얼마나 뚱뚱한지 (variance)로 나를 주위로 얼마나 weight를 줄 것인지 판단한다.

sigma
아래 사진을 보면 sigma(표준편차, standard deviation) 값에 따라 smoothing되는 정도가 다르다.
sigma는 Gaussian Distribution을 중심으로 대칭을 이루고 그 면적이 1에 해당한다. 아래 사진을 보면 sigma 값이 작을 수록 중심에 더 집중이 되고 값이 클수록 더 넓게 분포된 것을 알 수 있다.
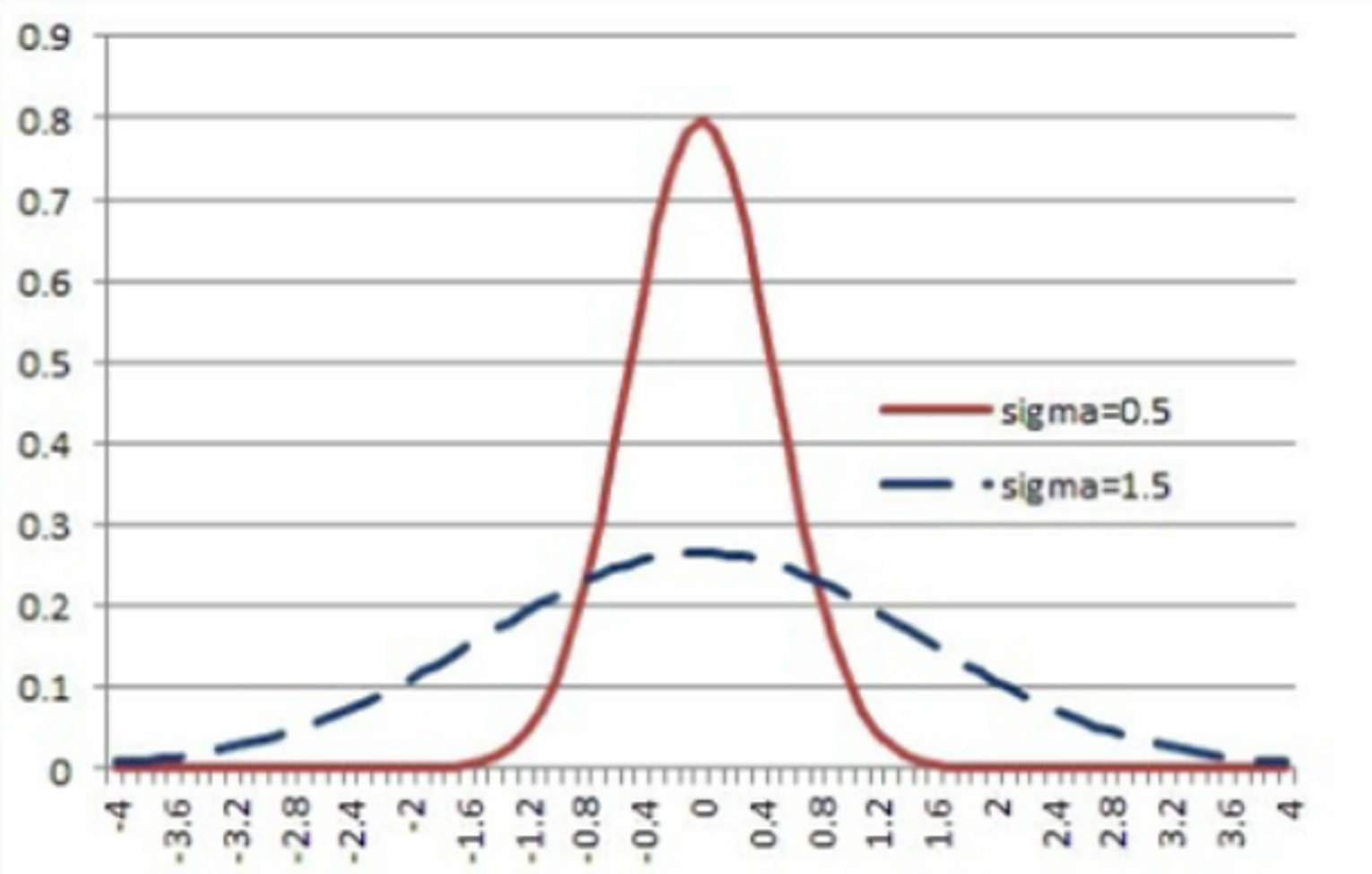
sigma값에 따라 다양한 결과를 가질 수 있다. sigma가 10일 때를 보면 본래의 내 정보가 너무 많이 사라지는 것을 알 수 있다. 따라서 상황에 따라 적절한 sigma값을 설정해야 한다.

📌 Smoothing before Derivative Operator
처음 우리는 이미지를 미분하여 특성을 찾아내고자 했다. 그런데 미분을 하니 noise 가 많아 우리가 원하는 것을 찾지 못했다. 이에 미분을 하기 전에 smoothing을 적용시키려 한다.
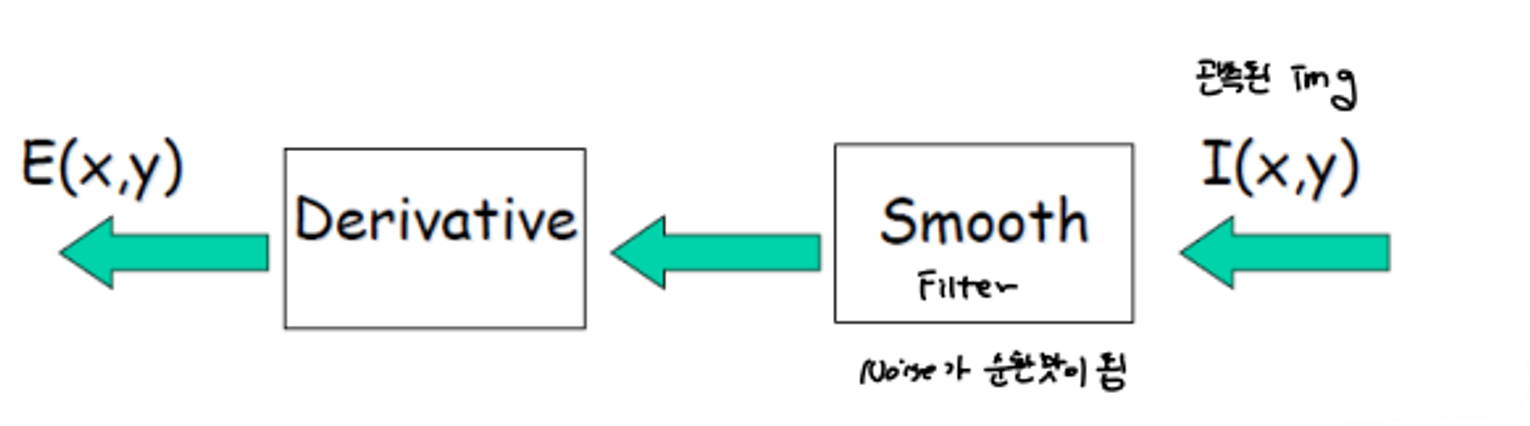
사실 미분과 smoothing 적용시키는 것 모두 convolution을 계산하는 것이다. 이에 convolution의 commutative한 특징을 사용하여 kernel끼리 먼저 convolution을 한 후 결과를 이미지랑 convolution을 한다. 이를 통해 성능을 올릴 수 있다.
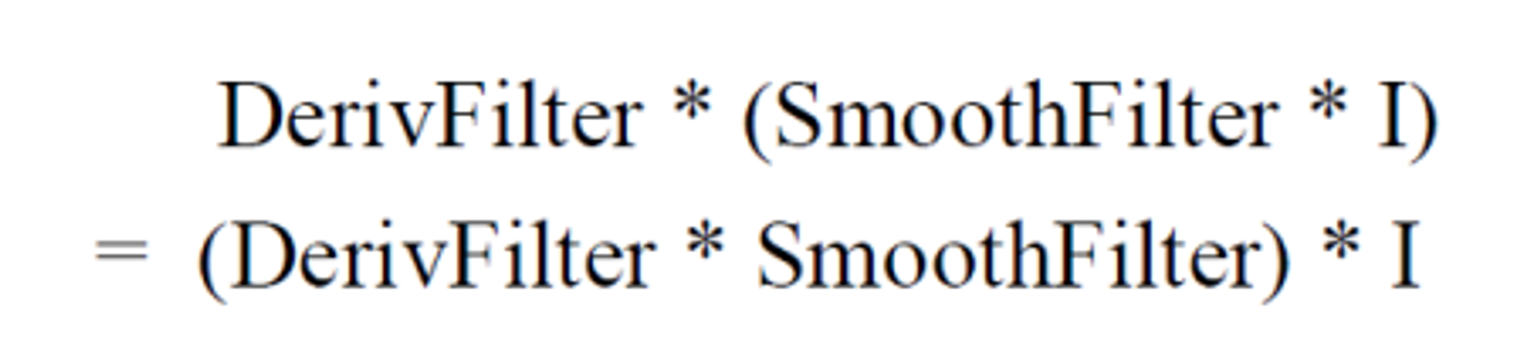
First Derivative of a Gaussian
가우시안을 미분하면 다음과 같다.
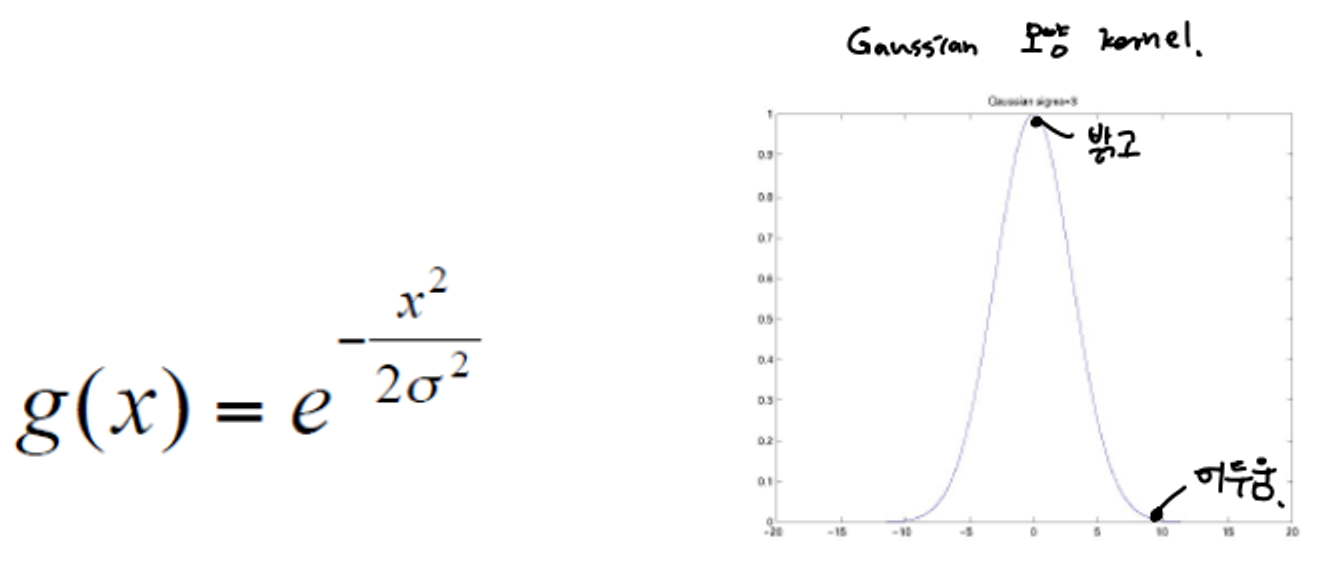
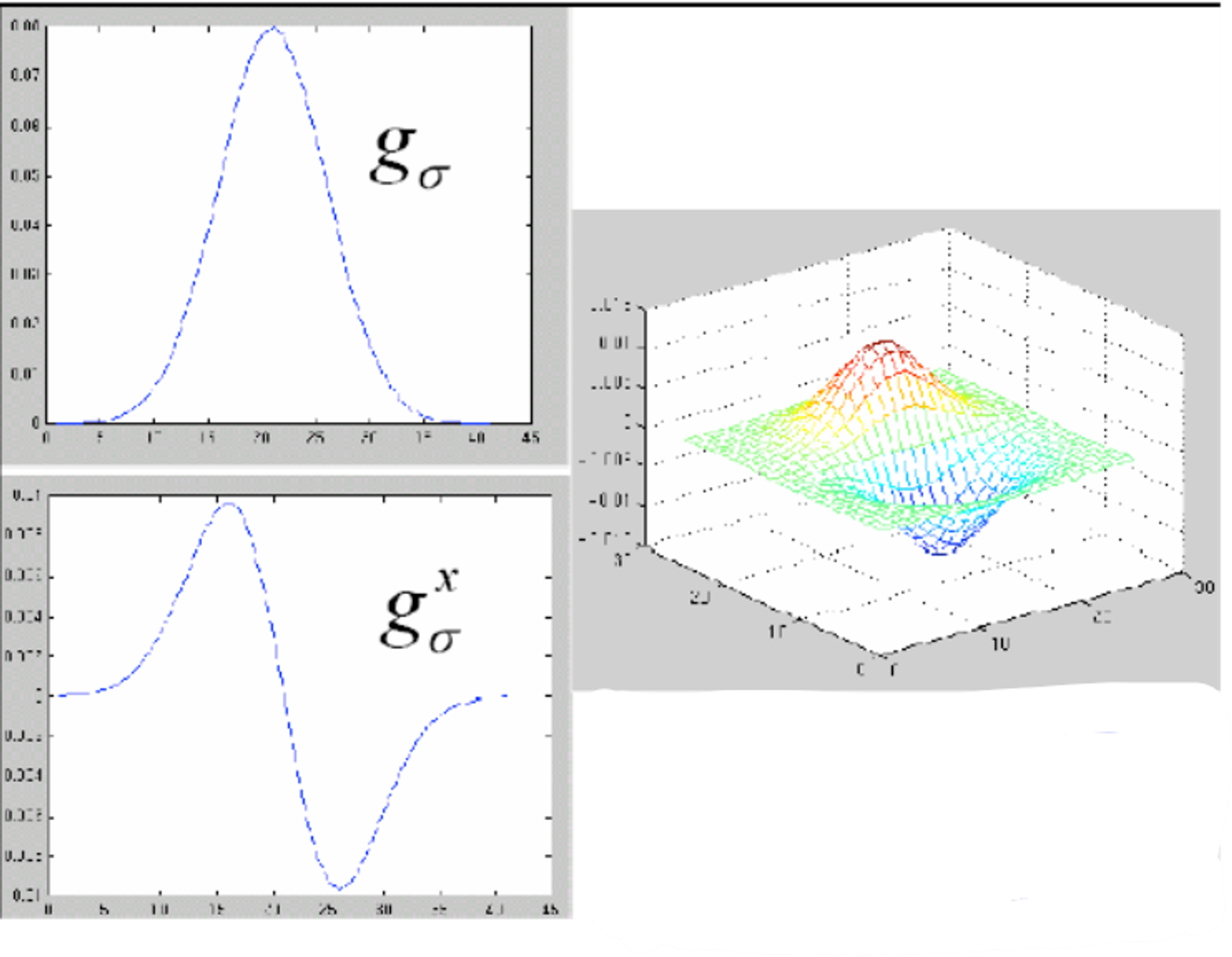
Derivative of Gaussian Filter
스무딩을 위해 사용할 가우시안과 특징을 찾기 위한 미분 과정을 합쳐서 하나의 필터로 만들었다.
필터의 모양은 아래와 같다.
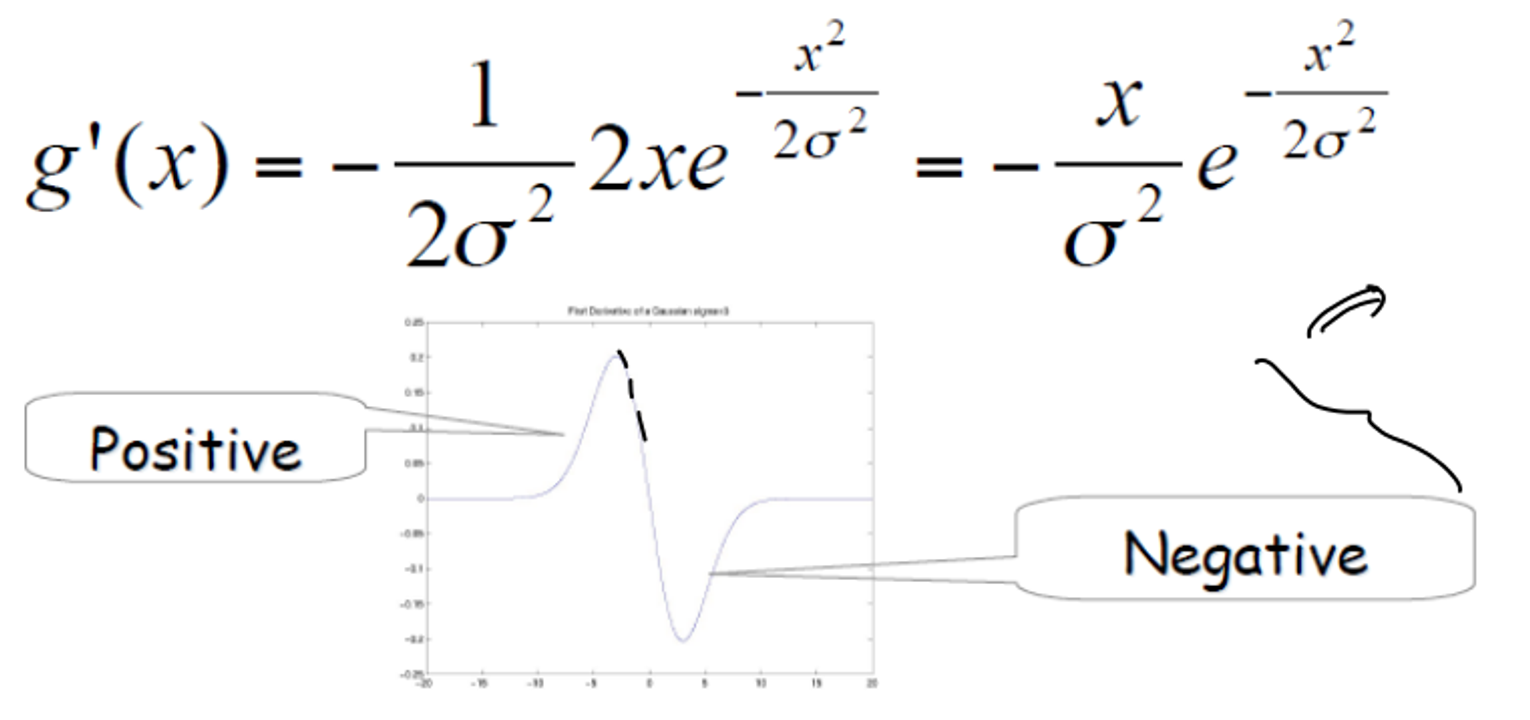
만약 아래처럼 나오는 결과를 급격하게 변하는 절벽과 같은 값으로 만들고 싶다면 가우시안의 표준 편차 값을 작은 것을 사용 (picky) 하면 된다.

📌 Edge Detection
💁♀️ What are edges?
- 값(밝기, color, …)이 다른 부분의 경계선
- low level에서 edge는 값의 차이가 나는 경계이다
voundary: edge 중 의미를 가지는 영역을 가르는데 결정적인 역할을 하는 것

✅ Edge Detection (1D)
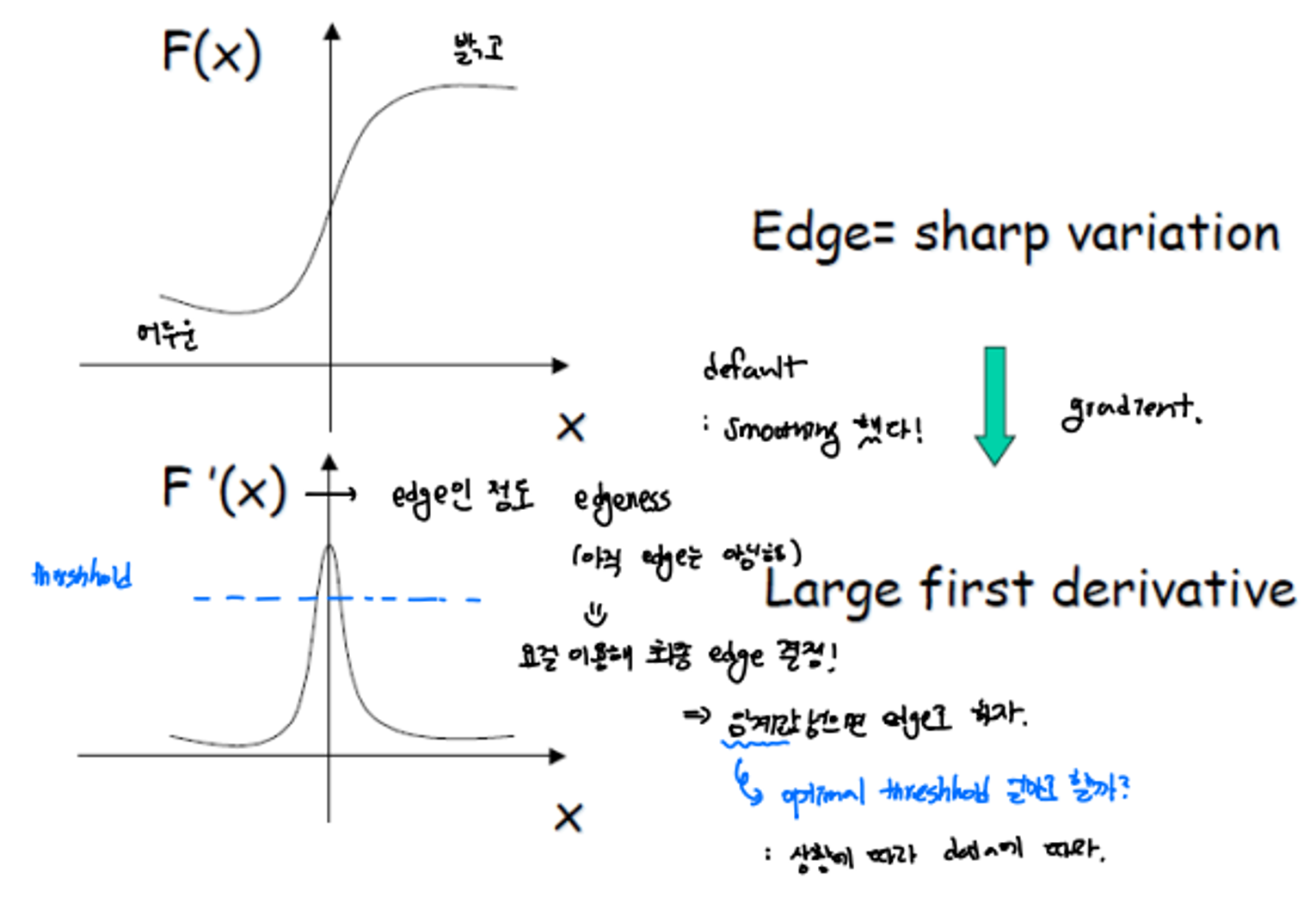
F(x) 함수를 보면 픽셀 값이 한 쪽은 어둡고 한 쪽은 밝은 것을 볼 수 있다. 이 함수를 한 번 미분한 F’(x)를 우리는 edge인 정도라고 이야기 한다. 하지만 아직 edge는 아니다.
이제 여기서 edge를 찾기 위해 threshold를 설정한다. 그리고 이 임계값을 넘으면 edge로 보기로 한다.
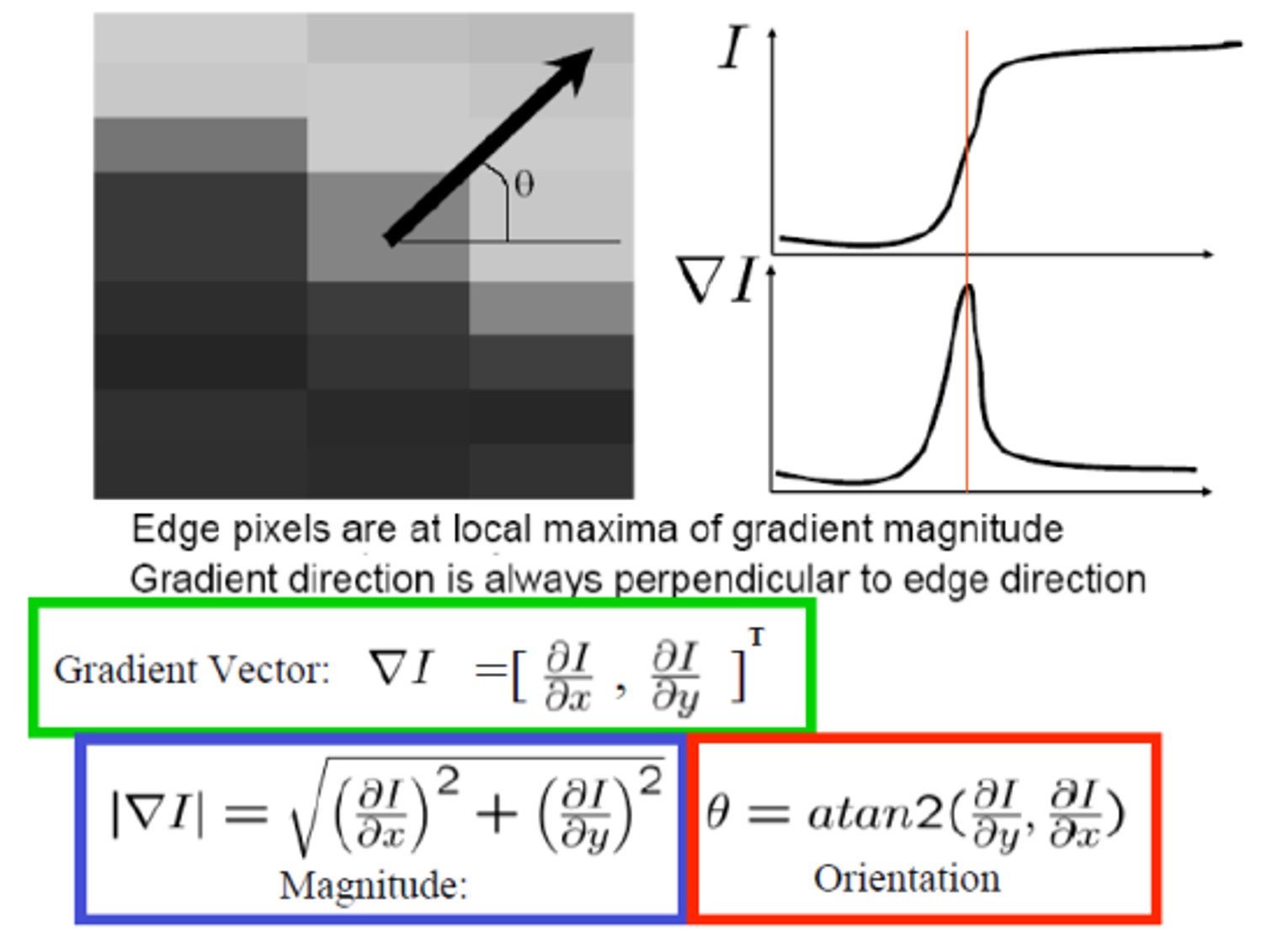
overview of Gradient
- magnitude : edge가 어느 정도인지
- orientation : 어디를 보고 있는지
How should we choose the threshold?
미분을 하여 threshold를 정해 edge를 찾는 방법에는 문제점이 존재한다.
- 원하는 것과 원치 않는 것이 같이 사라진다.
- threshold가 80인 사진을 보면 배경과 풀밭에 대한 edge는 걸러냈지만 사람의 다리에 대한 edge 정보도 사라진 것을 볼 수 있다.
- edge가 thick해진다.
- threshold를 작게 잡을 수록 edge가 두꺼워져 면적을 갖게 된다.
⇒ 그러나 edge detection을 통해 하고자 하는 것은 선을 찾는 것이다. 즉, 면적을 접하면 안된다는 것이다. 얇을수록 좋고 두꺼울수록 왜곡된다.

📌Canny Edge Detector
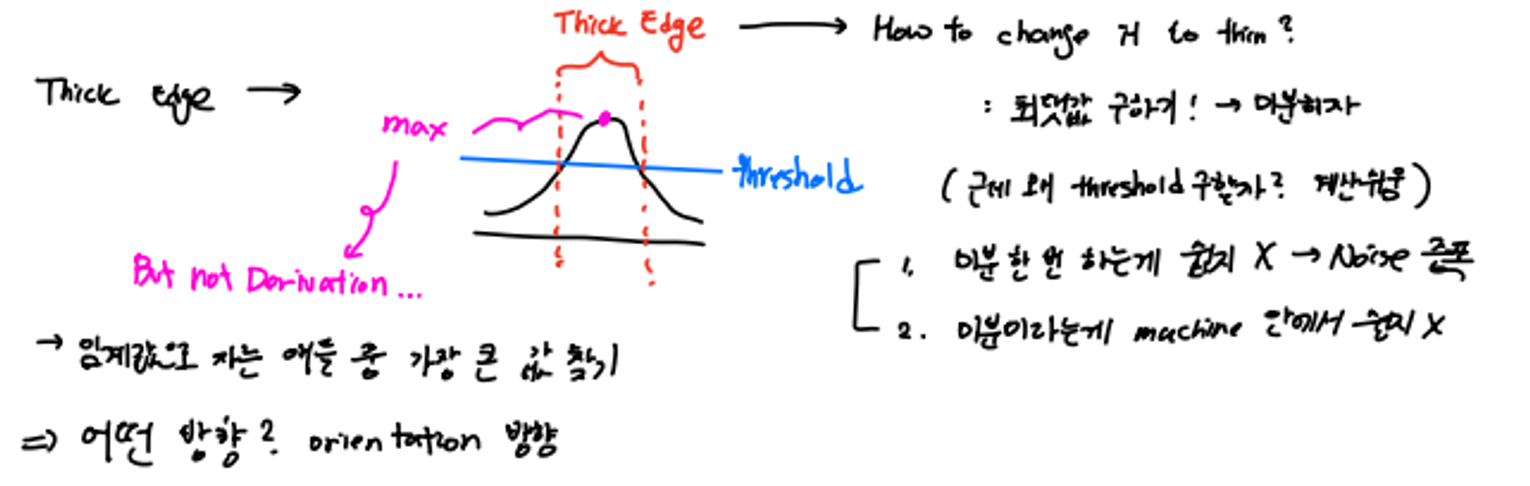
How to make edge thin?
threshold를 정하는 것 때문에 edge가 thick해지는 일이 발생했다. 그러면 어떻게 edge를 얇게 만들 수 있을까? 방법은 간단하다 최댓값을 구하면 된다!
- 미분을 하자
- 미분하는 것은 쉽지 않으며 noise를 증폭시킨다.
- 미분이라는게 machine 안에서 하기 쉽지가 않다.
- 임계값으로 자른 것들 중 가장 큰 값을 찾는다.

Trade-off
Smoothing←→Localization
스무딩을 많이 할수록 edge는 더 thick해진다.

✅ Canny Algorithms
concept
threshold를 여러개 고른다. 그리고 애매한 애들 중 강한 애들 근처에 있는 것은 살리는 방식으로 사용한다.
-
노이즈 제거를 위한 가우시안 필터링
-
gradient 계산 ( 방향 & 크기)
-
NonMax Suppression or Non-maximum suppression
⇒ Thick Edge problem solution
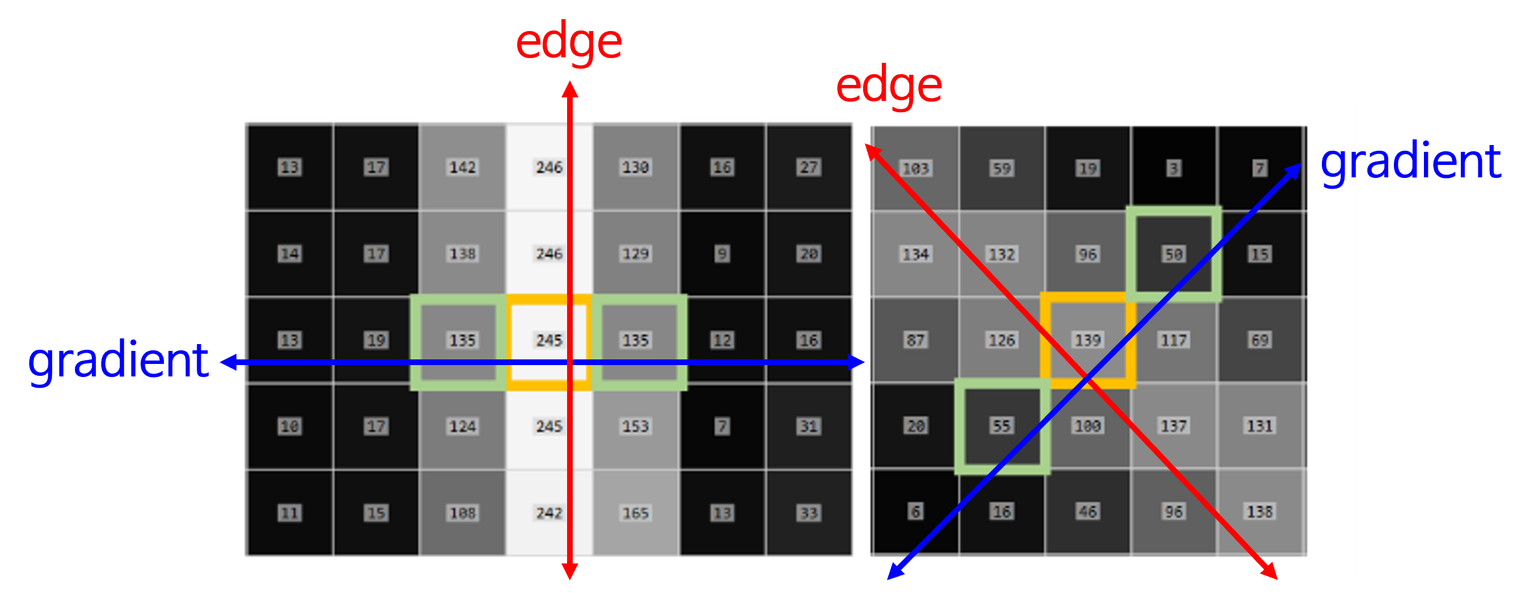
- 하나의 edge가 여러 개의 픽셀로 표현되는 현상을 없애기 위하여 gradient 크기가 local maximum인 픽셀만을 edge 픽셀로 설정
- gradient 방향에 위치한 두 개의 픽셀을 조사하여 local maximum인 지 확인
- 아래 그림과 같이 edge와 gradient는 직교입니다. 따라서 gradient의 방향을 기준으로 NMS를 적용하기 때문에 단일 edge를 선택
-
Hysteresis edge tracking
⇒ 원하지 않는 값이 사라지는 문제 해결
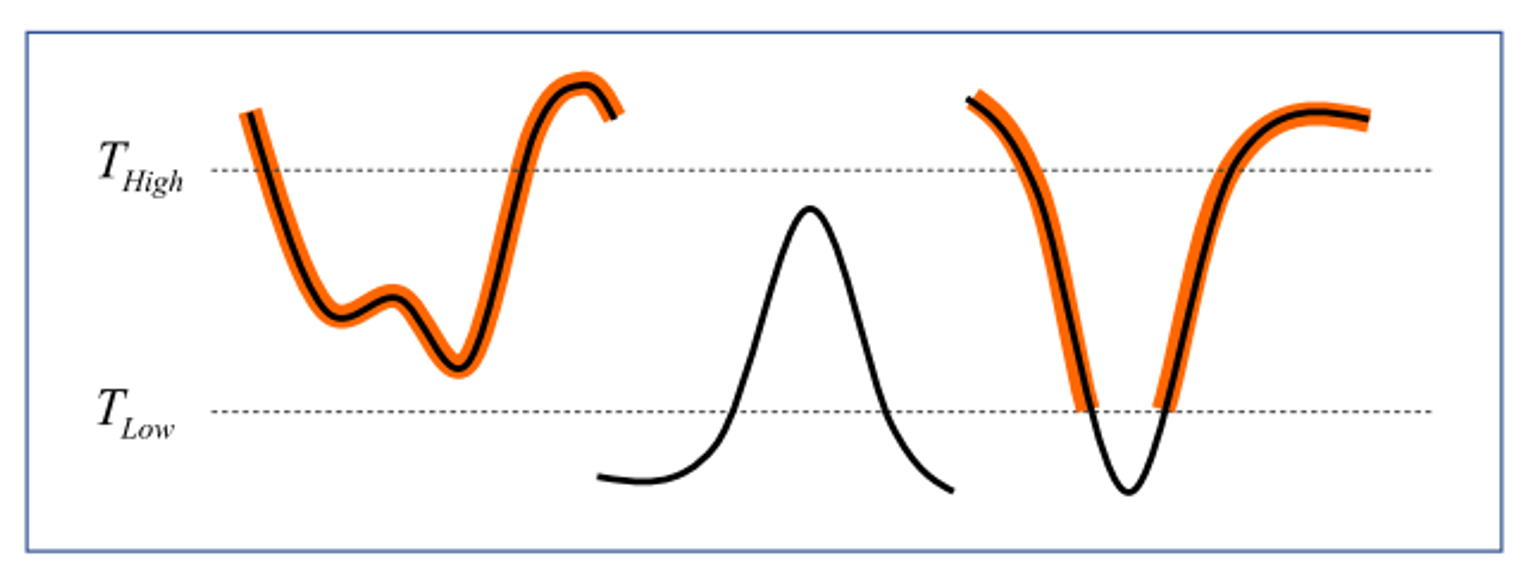
- 두 개의 임계값을 사용하며 edge로 판별할 수 있는 기준이 두가지 영역으로 구분
- High Threshold 이상의 값을 가지는 픽셀은 edge로 판단 →
strong edge - Low threshold 이하의 gradient를 가지는 픽셀은 edge가 아니라고 판단
- High Threshold과 Low threshold 사이의 픽셀
→ 픽셀들을 계속 이어갔을 때 High Threshold 이상의 값을 갖는 픽셀과 연결이 된다면 hysteresis 구간의 픽셀을 모두 edge로 판별
→weak edge