[Computer Vision] Stereo

💭 Summary
두개 이상의 뷰가 주어졌을 때 잃어버린 정보를 복원할 수 있는 방법에 대해 알아보고자 한다.

외눈박이일 경우 공간적으로 인식을 하는 건 불가능하다.

두 개의 뷰가 있을 때 어떻게 3차원 정보를 복원하는지 알아보자.

✅ Camera Projection Equation

computer vision

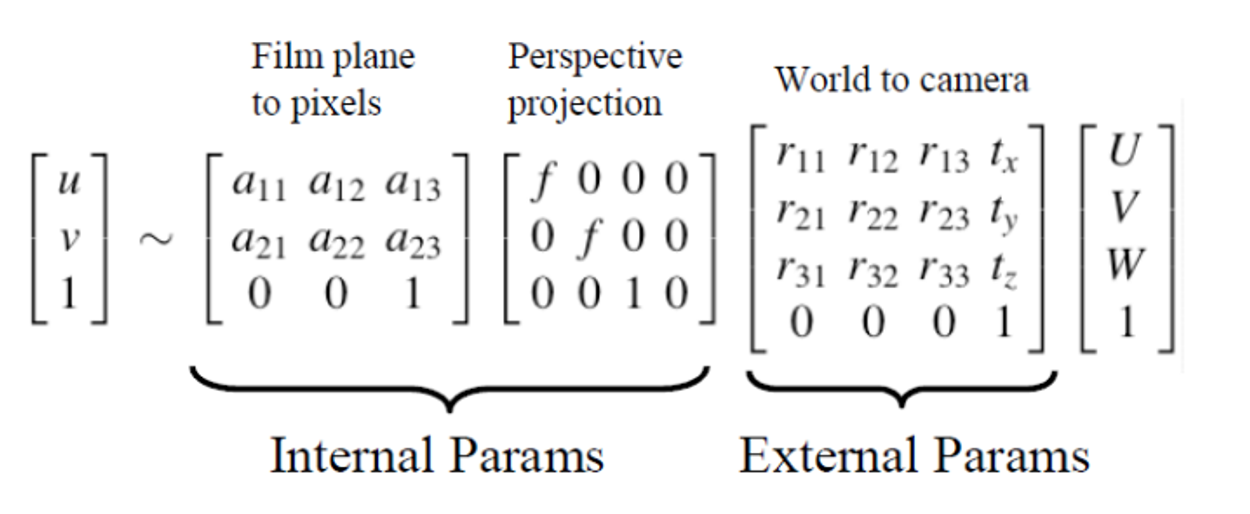
[u v 1] 의 given data, 찍은 사진으로 3D data의 복원을 하고 싶다.

Computer Graphics

[U V W 1]이 given data이다.

• world → camera
  카메라가 1개보다 많아 공동좌표가 필요할 때 이 작업을 수행한다.
  
• perspective projection
  → 3D에서 2D로 변환이 되기 때문에 사진을 찍으면 절대 Scale을 알 수 없다.
  

✅ Stereo Vision

동시에 2개 이상의 카메라에서 찍힌 사진을 통해 depth를 추론해는 것이다.

✅ Why Stereo Vision?

fundamental ambiguity

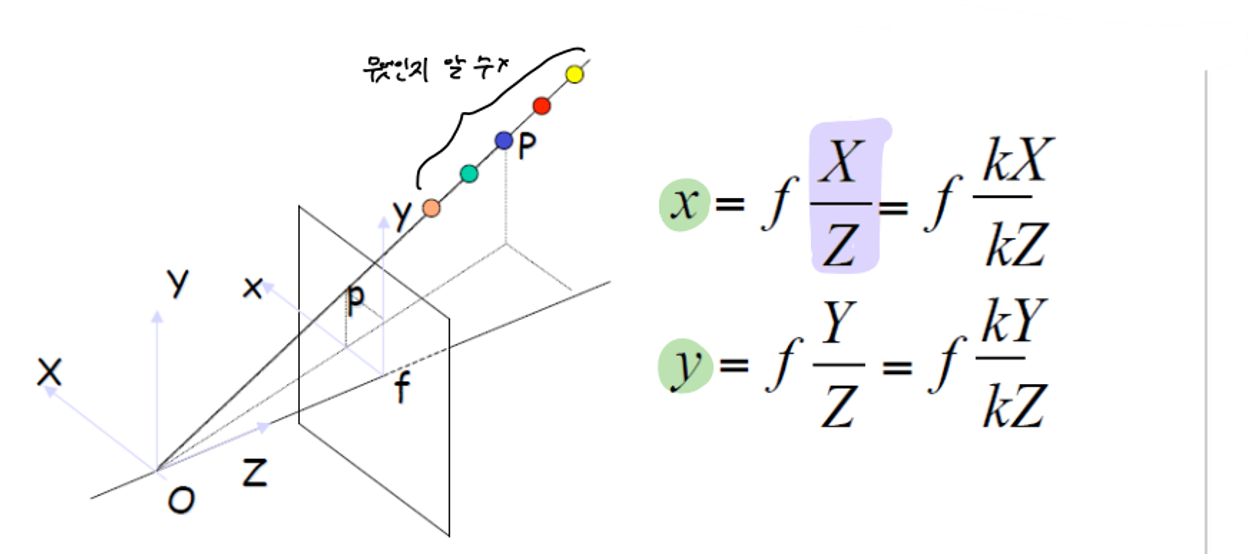
이전 시간에 배운 것처럼 계산을 할 때 아래 사진에서 처럼 X/Z의 하나의 pair만을 구하기 쉽지 않다.

→ OP 위에 점들 중 어떤 것인지 알 수가 없다.

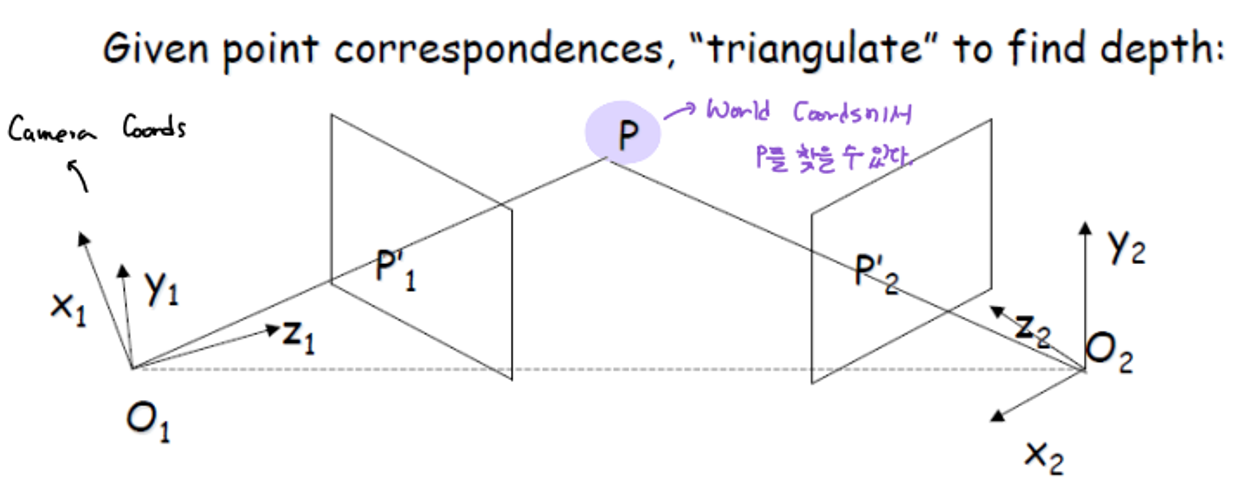
✅ Recovering Depth Information

위에서 언급한 문제 해결을 위해 우리는 카메라 두 개를 사용한다. 마치 우리의 눈처럼 말이다.

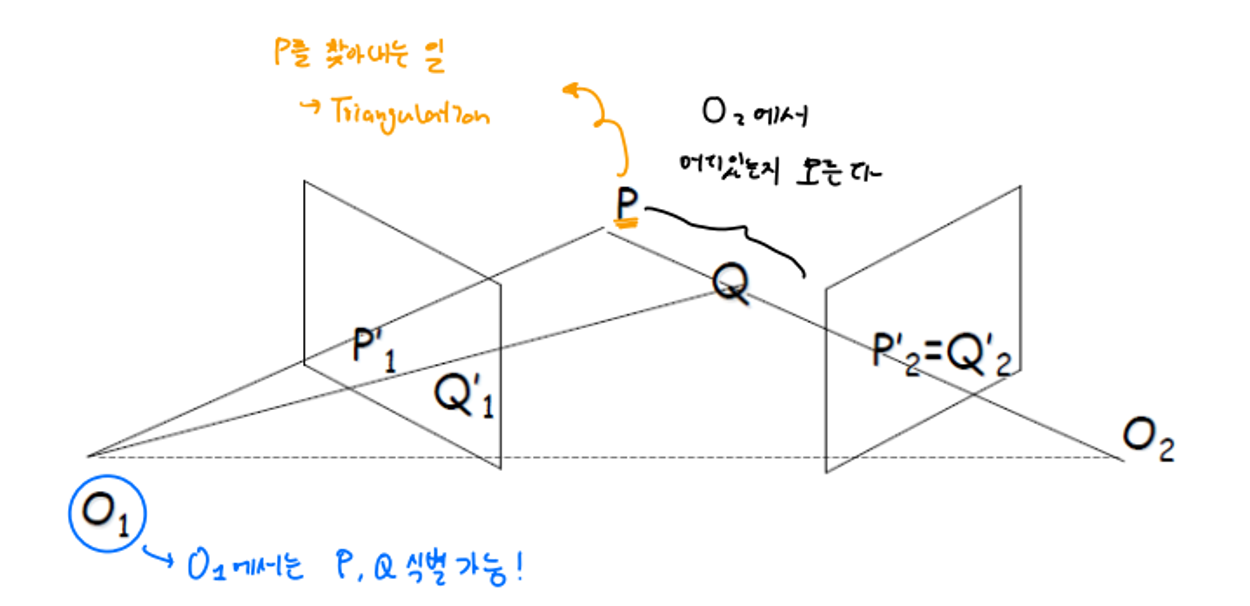
P라는 곳을 찾고 싶다고 가정했을 때

• O2에서 P, Q는 같은 직선상에 있기 때문에 어디에 있는지 알 수 없다.
• O1에서는 P, Q를 식별 가능하기 때문에 P를 찾아낼 수 있다.

→ 이렇게 P를 찾아내는 일을 Triangulation 이라고 한다.

A Hitchhiker’s Guide to Parallax

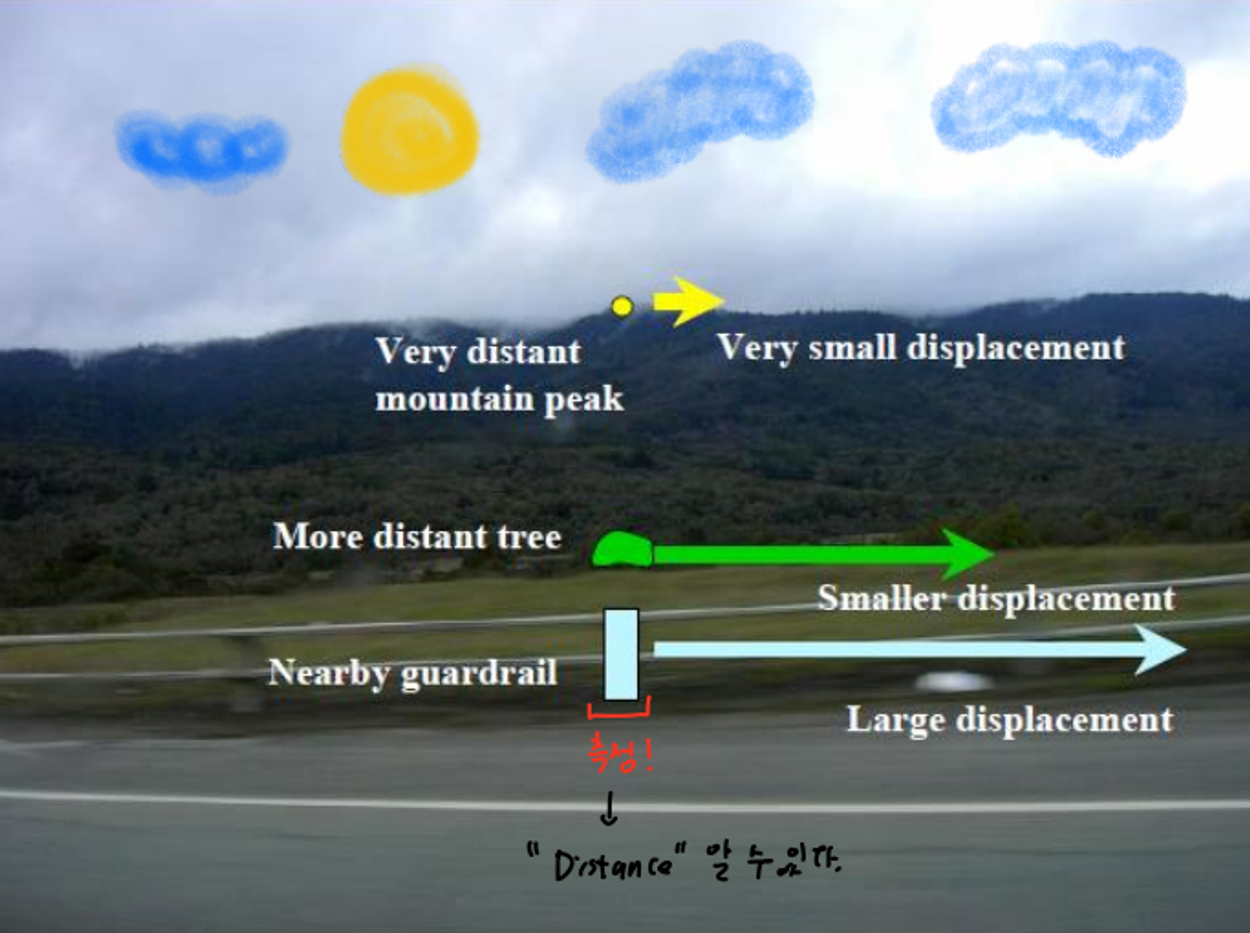
parallax : 다른 거리에 위치한 장면 특징의 겉보기 움직임

• motion parallax

  → 움직이는 시점 기준

  • 가까우면 : 빨리지나감
  • 멀면 : 느리게지나감

• 측정 방법

  1. sparse
     • 정밀도가 올라간다.
     • 얼굴만 측정
  2. dense
     • 정밀도는 떨어지지만 형상을 구할 수 있다.
     • 눈,코, 입, 얼굴, 다~

Stereo Reconstruction

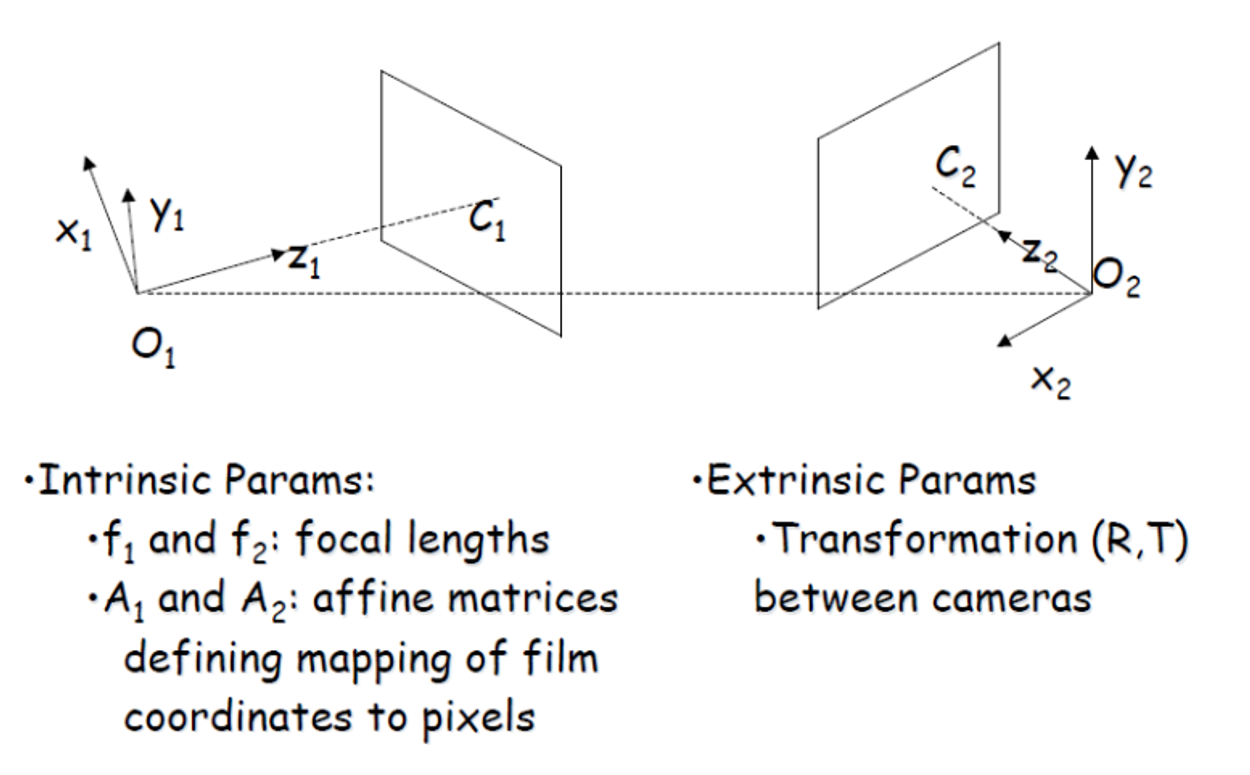
Parameters of a Stereo System

O1, O2 두 카메라는 같다.

→ perspective transform Matrix가 같고, affine transform에서 사용되는 f 값이같다.

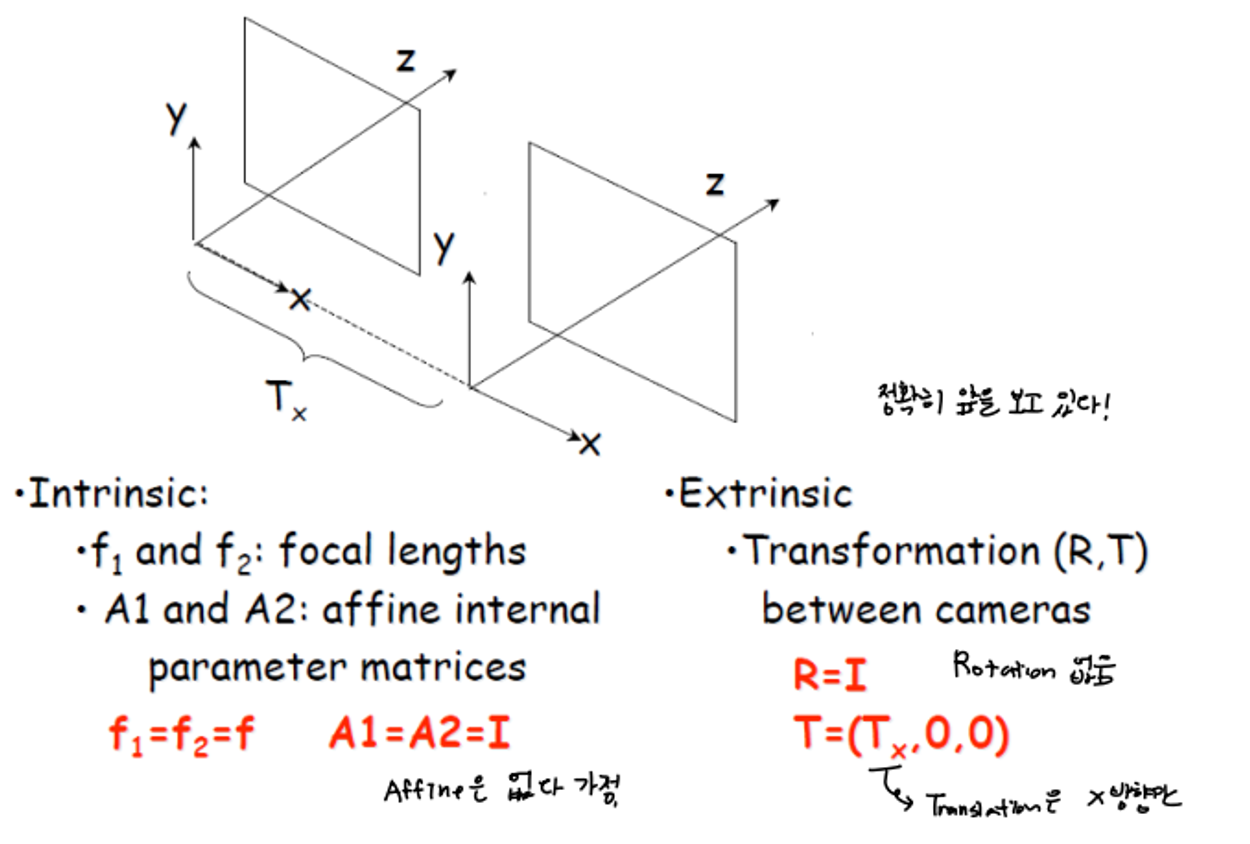
A Simple Stereo System

• 두 카메라는 정확히 앞을 보고 있다.
• Extrinsic (world → camera) : Transformation(R,T) 카메라의 rotation은 없으며 x축으로의 translation만 존재.
  
• Intrinsic
  • projection matrix : 초점 길이 f 가 모두 같다
  • Affine matrix : affine transform은 없다 가정

✔ Top Down View (XZ plane)

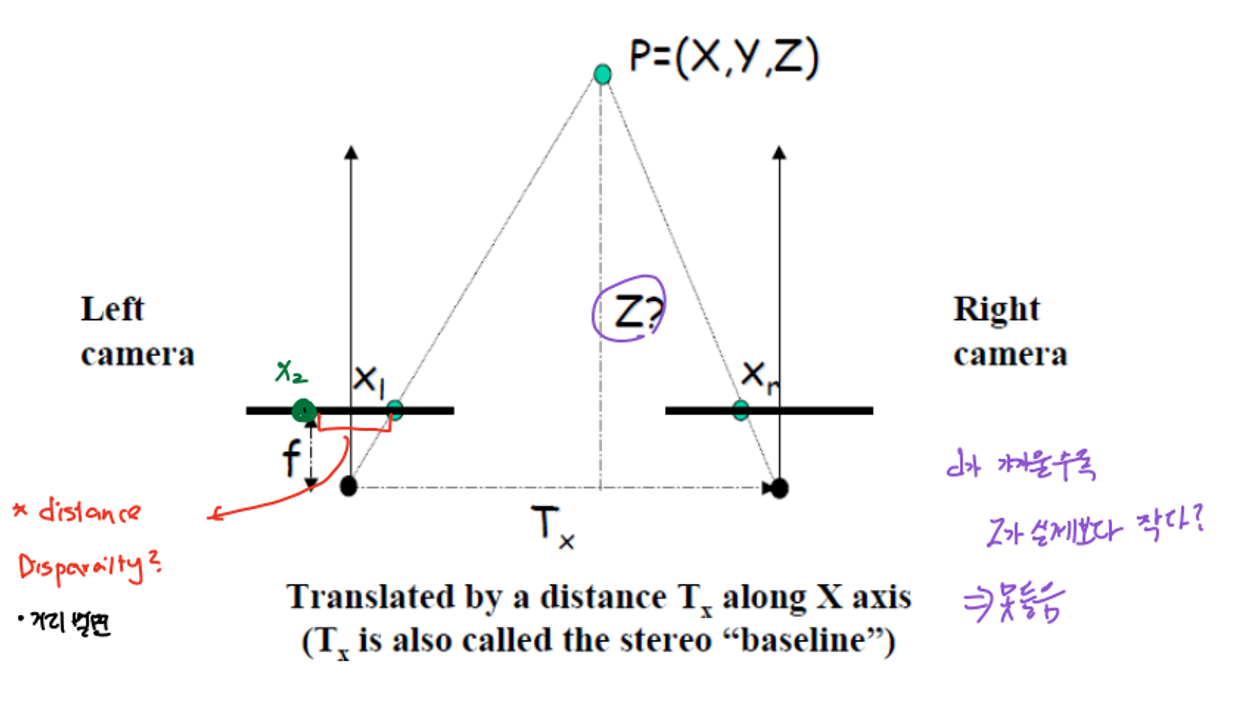
Projection Equations

Left Camera를 world Coordinate로 하고 right camera는 x방향으로의 translation만 있다.

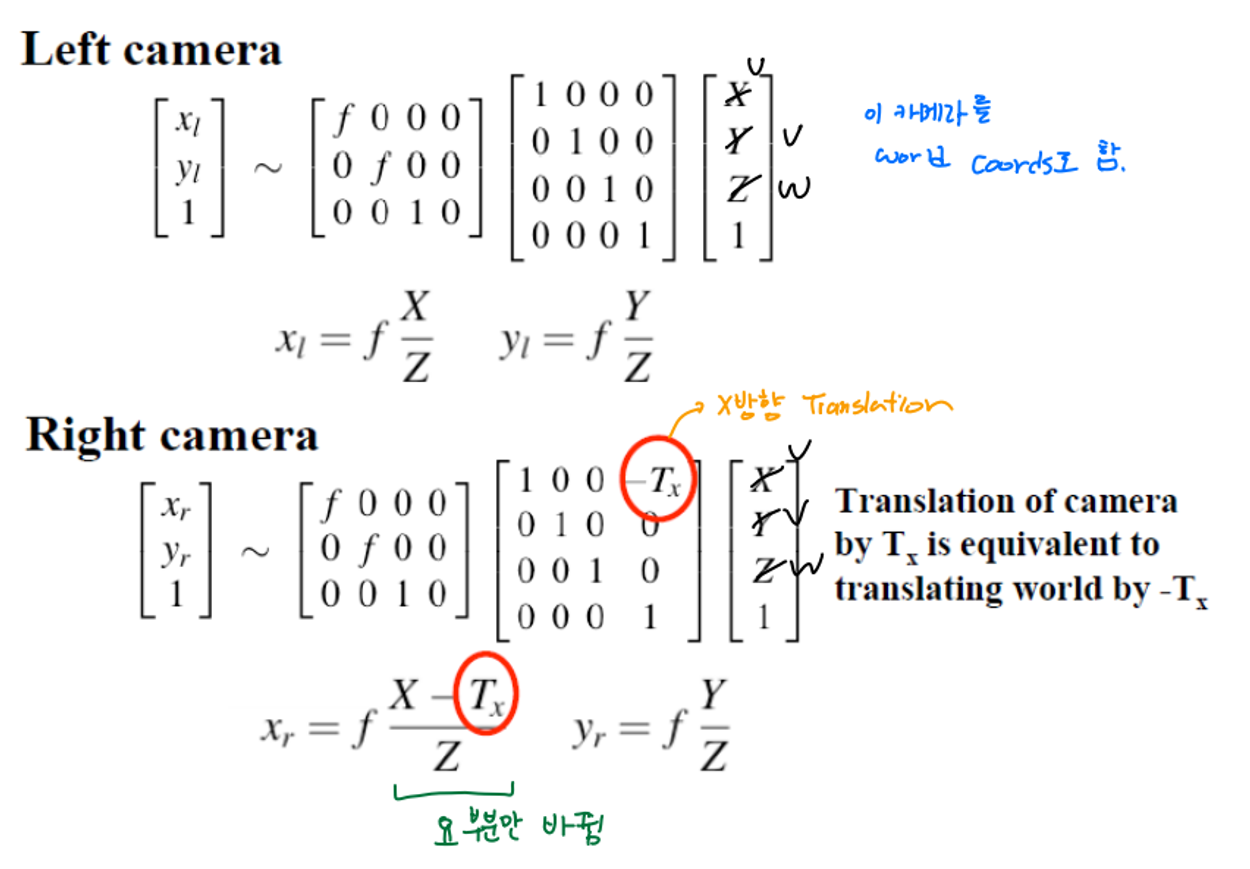
Stereo Disparity

두 개의 카메라 렌즈(또는 눈) 사이의 관찰 위치 차이에 의한 이미지 픽셀 간의 거리 또는 깊이 차이

→ 두 개의 이미지(좌측 이미지와 우측 이미지) 사이에서 대응되는 특징점 또는 픽셀의 위치 차이를 계산하여 3D 공간에서 객체의 깊이 정보를 추정하는 데 사용

Stereo Disparity : d

right camera와 left camera가 관측한 두 x값의 차이를 d라고 하자. 이 d는 아래와 같은 식으로 표현이 가능하다. 이 때 분모에 있는 Z와 바꾸어 식을 변형시키면 depth값을 구할 수 있다.

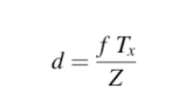
Depth : Z

$T_x$ , d를 모두 알고 있으니 우리는 Depth인 Z를 구할 수 있다.

⇒ depth와 stereo disparity는 역수 관계다.

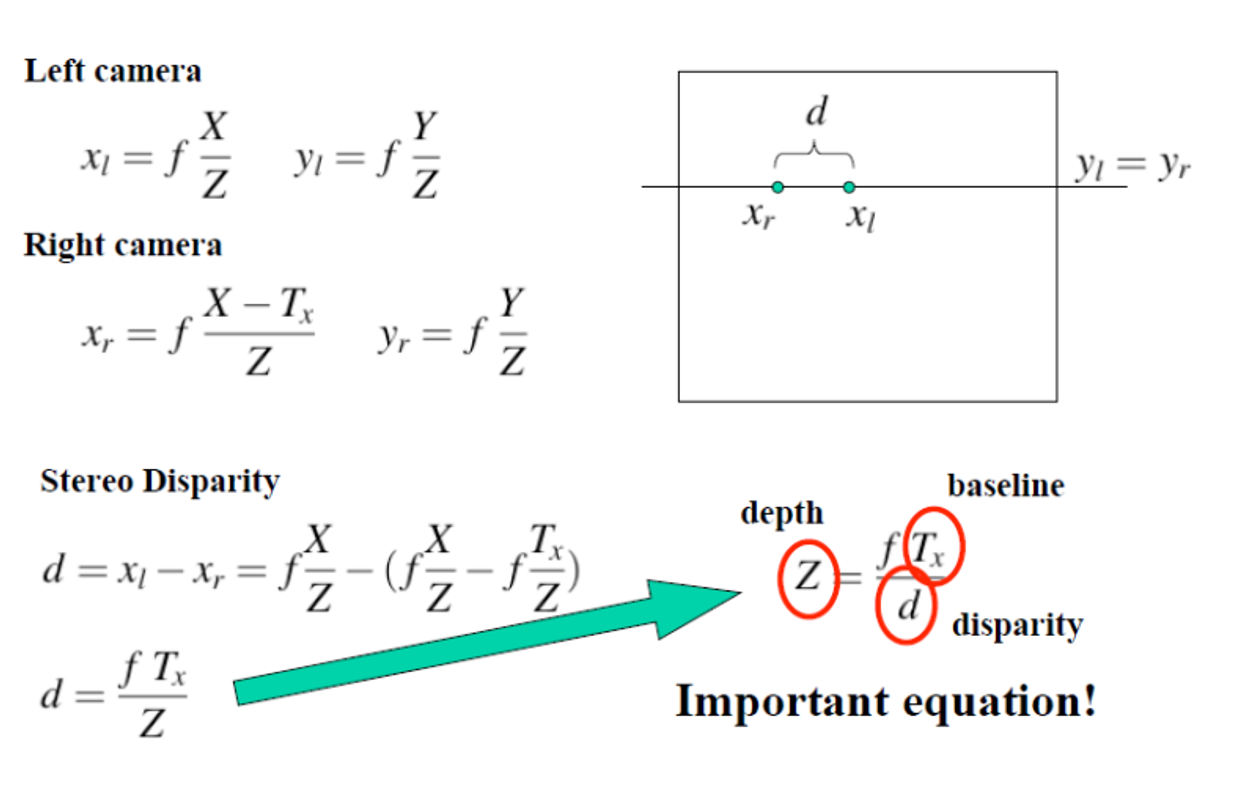
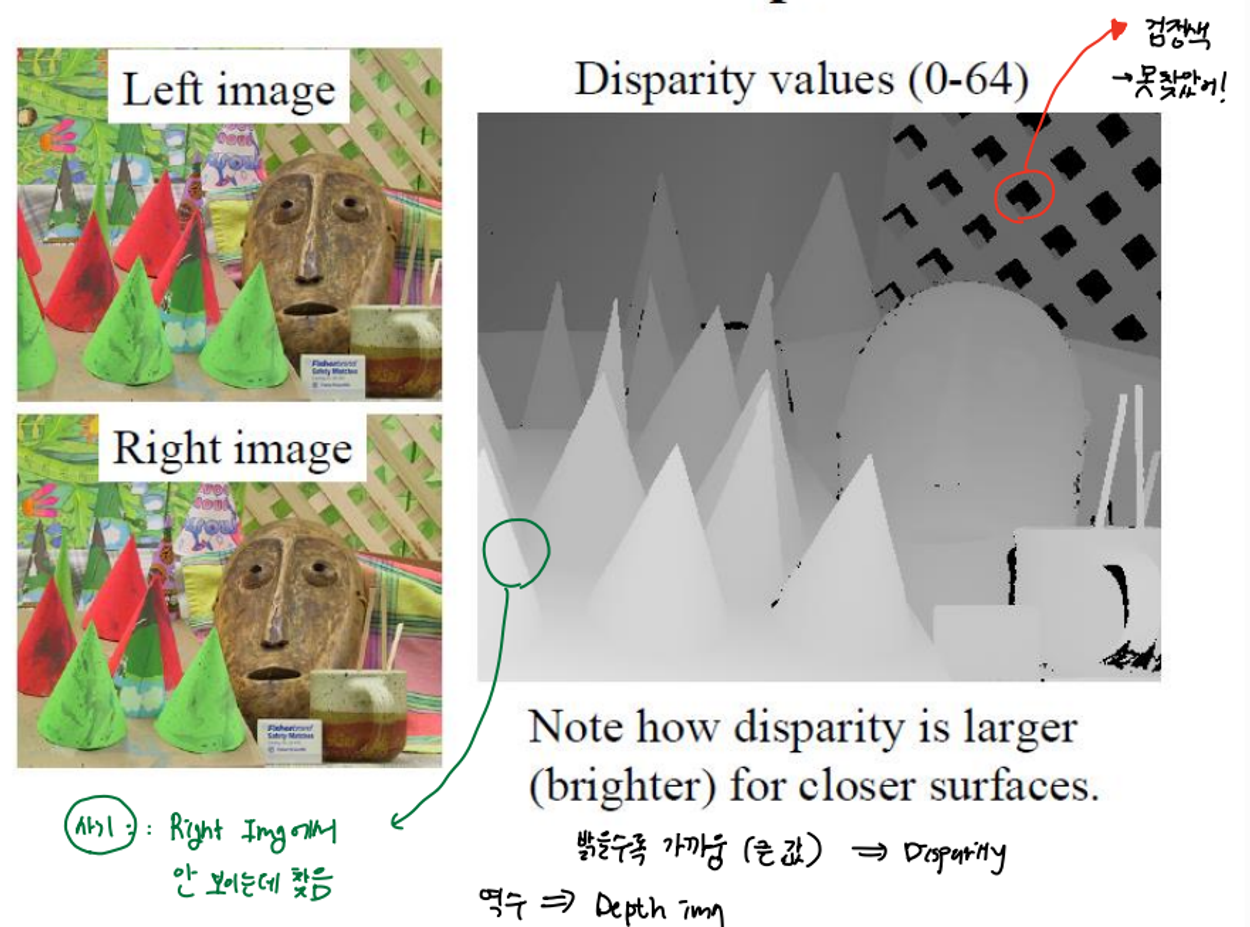
Stereo Example

오른쪽 사진은 disparity 결과이다. disparity 값이 크다는 것은 깊이가 얕다는 것이다. 이는 가까이 있는 것을 의미한다. 즉 아래 사진에서 가까이 있을 수록 밝게 표현된 것이다.

그리고 사실 아래 사진은 사기이다.

1. 왼쪽 부분은 한 쪽 Left image에서는 보이지 않는 부분인데 구했다.
2. edge가 저렇게 선명하게 나올 수 없다. patch를 떠서 cooresspondeing matching을 하는데 edge는 8-neighbor 값이 달라지기 때문에 저렇게 선명할 수가 없다.

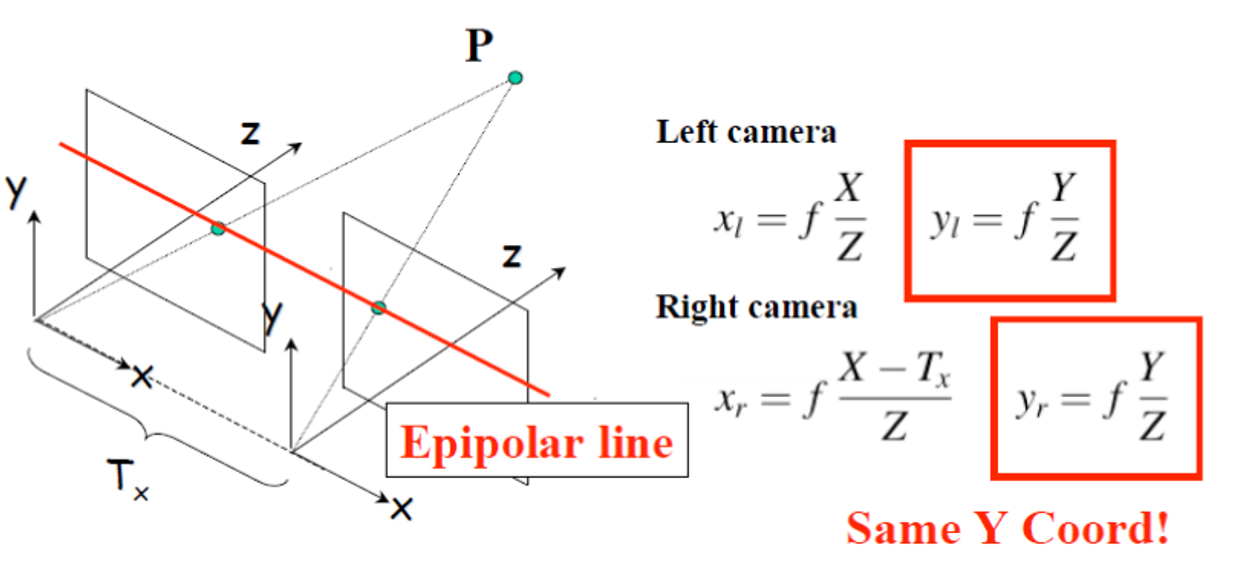
Epipolar Constraint

corresponding point를 찾기 위해서 전체 이미지를 다 보기엔 cost가 넘 크다.

1. 그러니 Epipolar Constraint 를 걸어 Epipolar Line 에서만 찾자.

• Epipolar Line: 두 카메라에 object가 찍힌 그 픽셀 point를 잇는 선
  x 방향으로만 translation했기 때문에, y값은 동일!
  

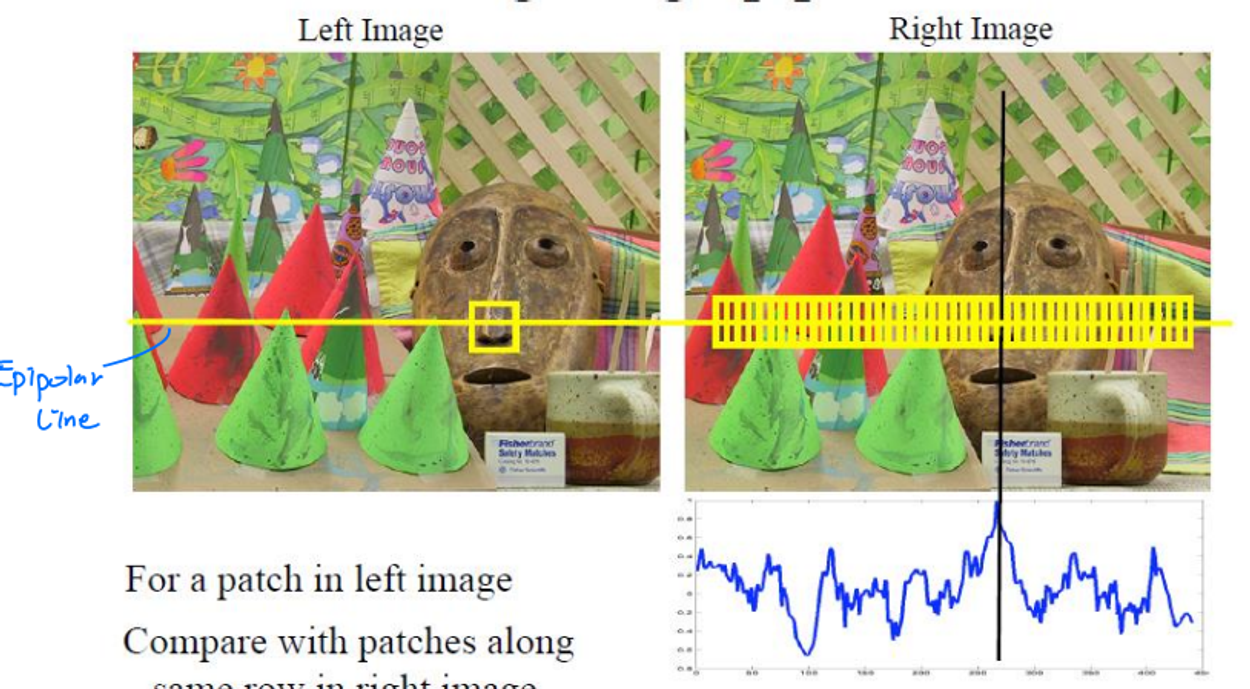
그런데 이것도 사실 다 볼 필요가 없다.

2. 오른쪽에서 본 이미지는 왼쪽 이미지를 기준으로 물체가 왼쪽으로 이동한 것 처럼 보이므로 patch의 왼쪽만 본다.

근데..! 사실 왼쪽도 다 볼 필요가 없다.

3. 두 카메라 사이의 거리인 baseline 범위까지만 확인해보면 찾을 수 있다.

Example

그래서 사실 사기가 아닌 사진으로는 이렇게 나오는 게 정상이다.

너무 퀄리티가 안 좋으니 개선이 필요하다.

kernel의 size를 키워서 narrow하게 말고, wide 하게 보자.

narrow한 영역은 noise에 민감하다.

• patch size가 작아지면
  • 퀄리티 좋아짐
  • 글로벌 옵티마 찾을 확률이 낮아짐
• patch가 커지면
  • 상대적으로 noise에 강해지지만, smooth해지면서 detail이 사라진다.
  • 경계 근처에 에러 디테일이 사라진다.
  • global optima pair 근처로 갈 확률은 높아지지만, 정확한 correspondence match는 어려울 수 있다.