Recurrent Neural Networks(RNN)
기존의 Neural Network는 고정된 크기의 벡터를 입력하고 고정된 크기의 벡터를 출력하는 단점이 존재했다.
하지만 RNN은 Vector Sequence에 대해 연산을 수행하기 때문에 가변적인 크기의 Vector를 입출력할 수 있다.
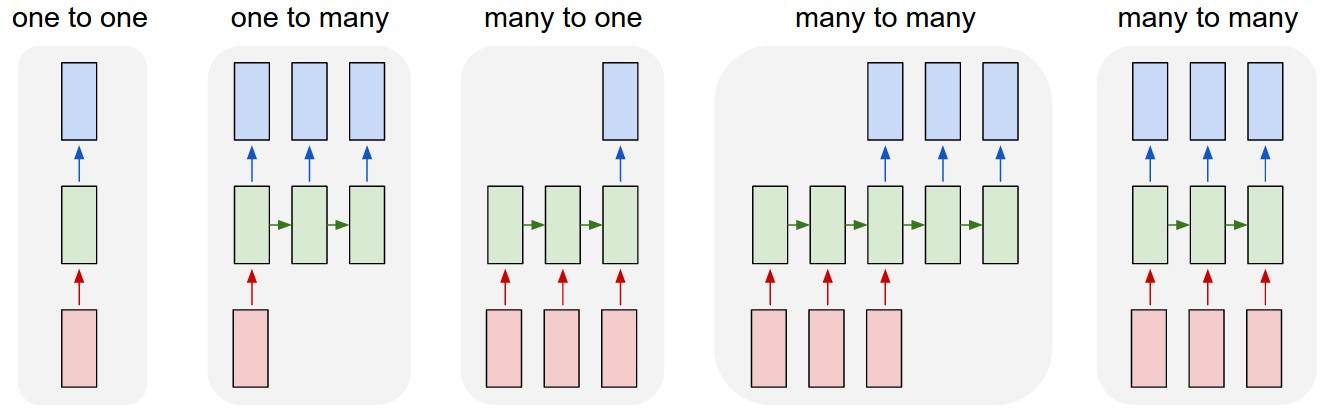
One to one
- 기존의 Neural Network 구조(RNN이 없음)
- 고정된 크기의 input과 output 출력
One to many
- input 1개에 대해 여러 개의 output을 가짐
- ex) Image Captioning(1개의 이미지 input -> sequence of words)
Many to one
- 여러 개의 input에 대해 1개의 output을 가짐
- ex) sentiment classification(sequence of words -> sentiment)
Many to Many
- 두 가지 종류가 존재
- 시간차가 존재하는 경우(machine Translation)
- 시간차가 존재하지 않는 경우(Video Classification on frame level)
Sequential Processing of Non-Sequence Data
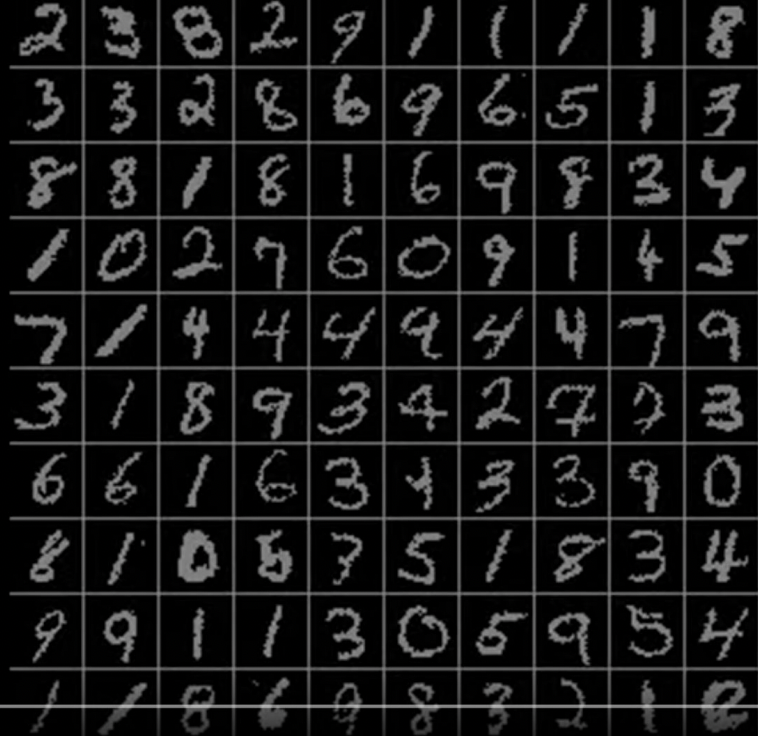
그렇다면 고정된 사이즈의 input과 output이 필요할 경우에는 RNN을 사용할 수 없을까? 그렇지 않다. sequential processing이 요구되는 경우에는 RNN을 사용할 수 있다.
위 이미지는 유명한 숫자 분류 문제이다. 비록 input으로는 fixed input이 들어가지만 숫자를 분류할 때 이미지 전체를 한 번에 살펴보는 것이 아닌 이미지의 부분 부분을 살펴보게 된다. 따라서 이미지 처리 과정이 가변 과정일 경우에는 RNN을 사용할 수 있다.

Recurrence Formula
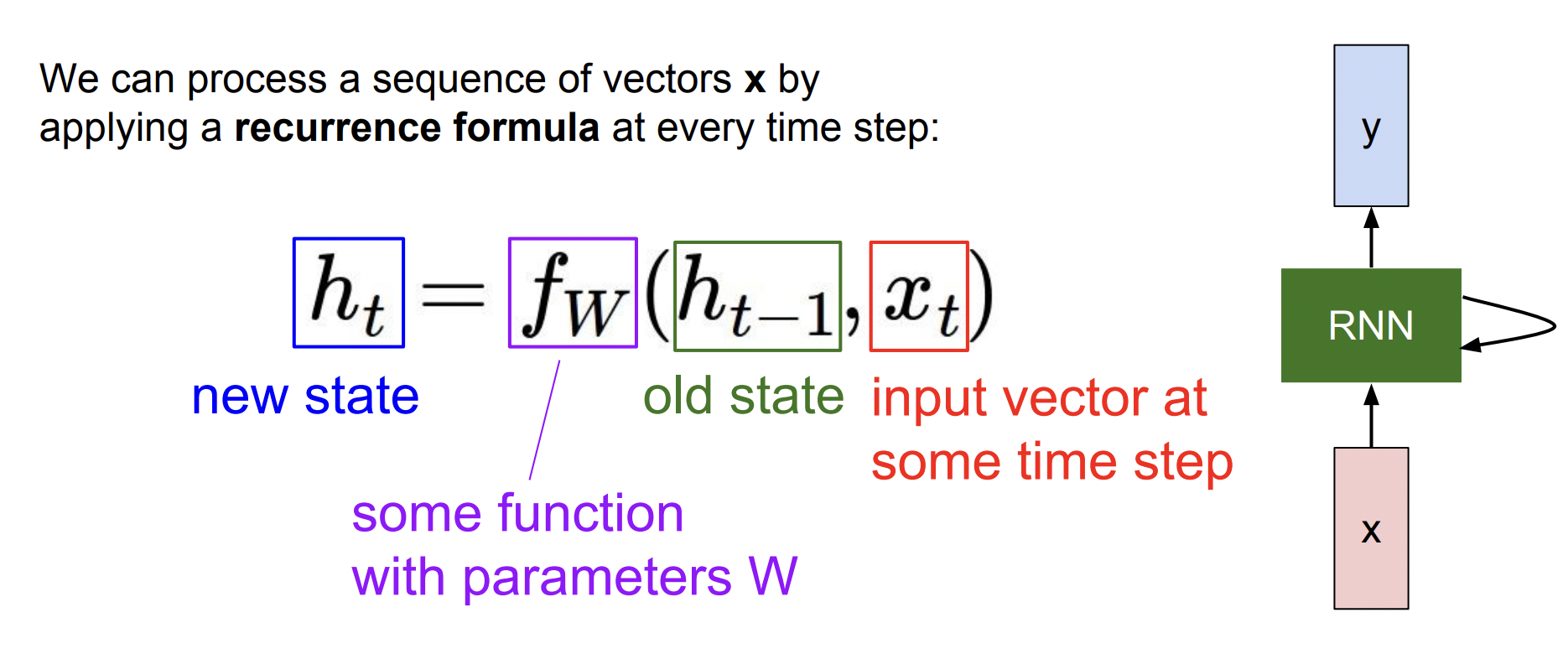
sequence vector인 x를 입력받고 함수 f를 지나 hidden state를 업데이트해서 출력값을 내보낸다. 이때 함수 f와 parameter w는 모든 step에서 동일한 값을 가진다.
참고로 RNN이 출력값을 가지려면 h(t)를 입력으로 하는 fc-layer를 추가해야 한다.
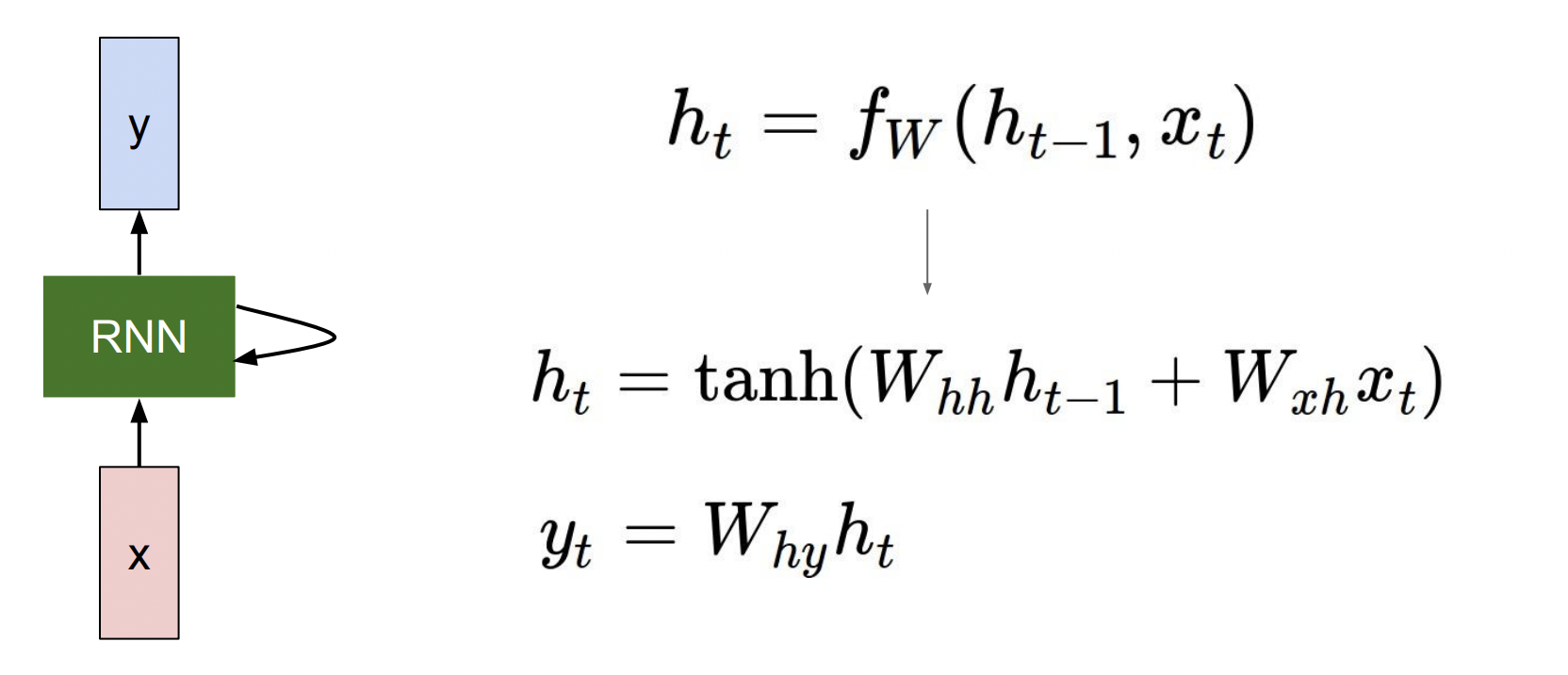
이 예시에서는 함수 f로 tanh 함수를 사용하였다.
RNN이 이러한 구조를 갖게 된 이유는 sequential process를 구현하기 위해서이다. sequntial한 구조에서는 이전의 데이터를 기억하는 것이 중요하기 때문이다.
computational graph
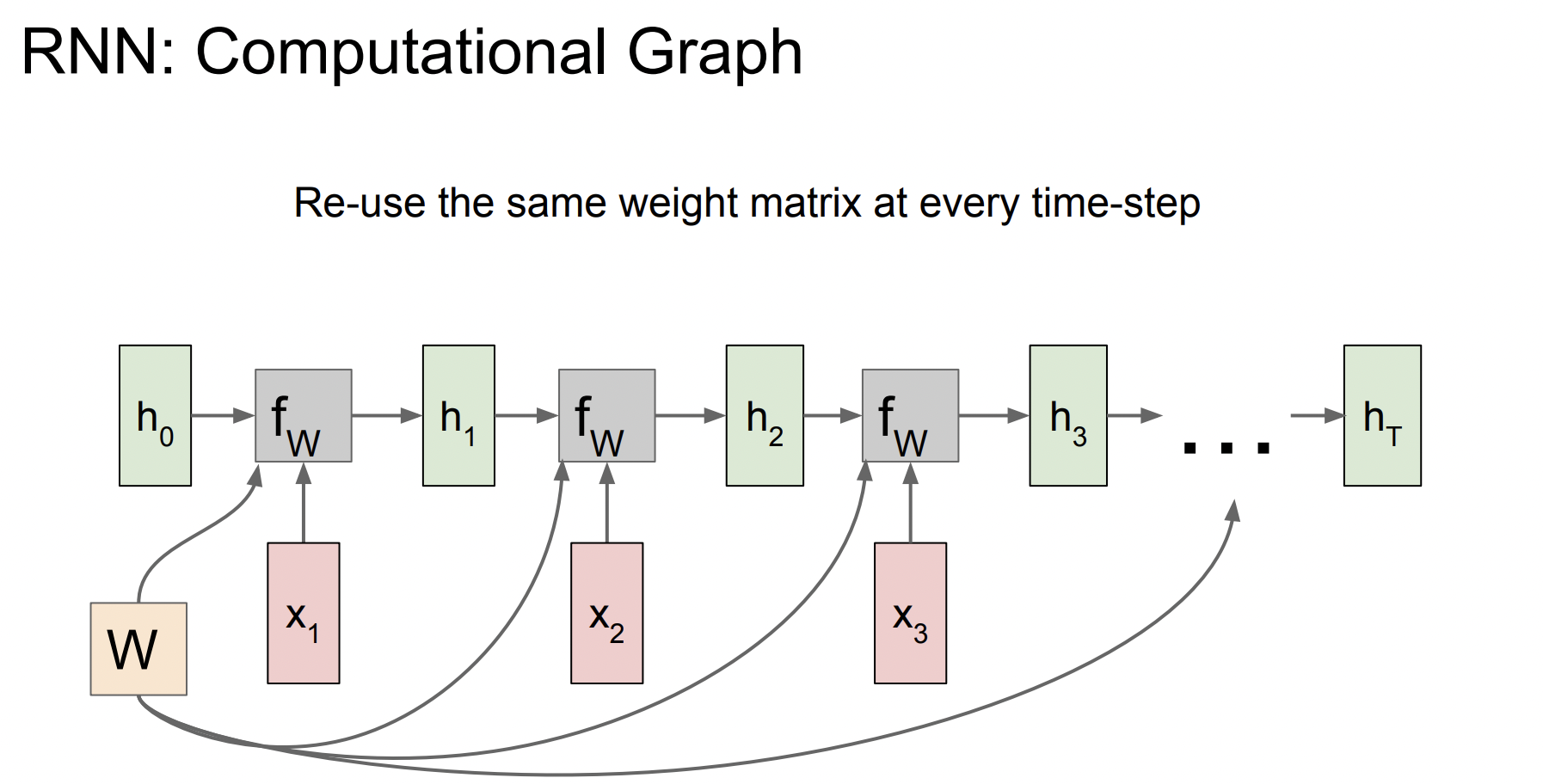
h0은 initial hidden state를 의미하고, 대부분 0으로 초기화된다. W는 가중치 행렬이고 매번 동일한 값을 사용한다. 이렇게 해서 h1이 나오고 그렇게 나온 h1이 그 다음 step의 입력값으로 사용된다.
many to many
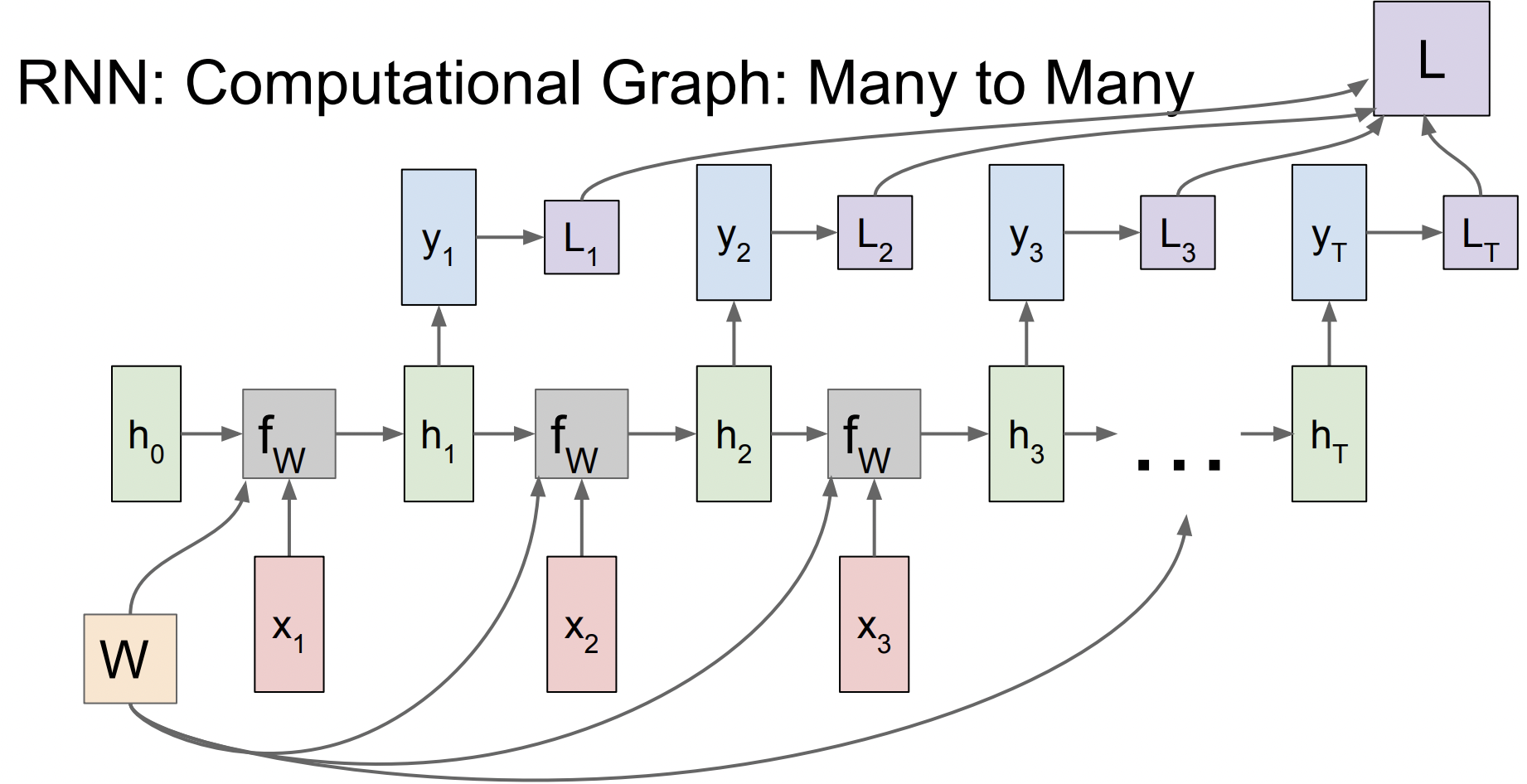
출력값이었던 h(t)가 그 다음 step의 입력이 되어서 y(t)를 출력한다. 이때 y(t)는 매 step의 class score를 의미한다.
이 graph에서 loss를 계산할 때에는 각각의 y에 대한 loss를 계산하고 이 loss들을 더해서 최종적인 loss가 되는데, 여기서의 loss는 softmax loss를 의미한다.
many to one
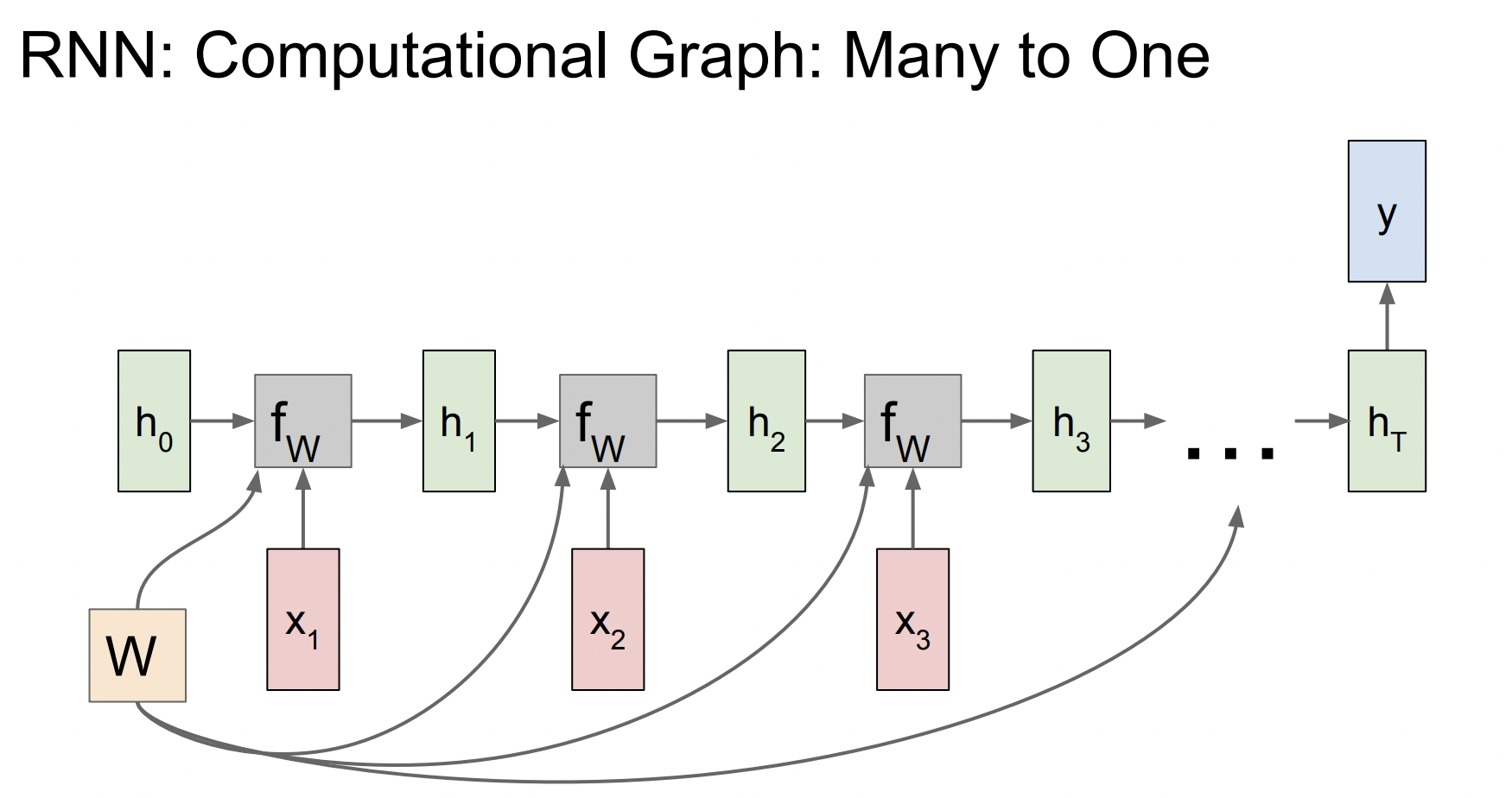
이 그래프는 네트워크의 최종 hidden state에서만 결과값이 나온다. 따라서 최종 hidden state가 전체 seqence에 대한 일종의 요약이라고 할 수 있다.
one to many
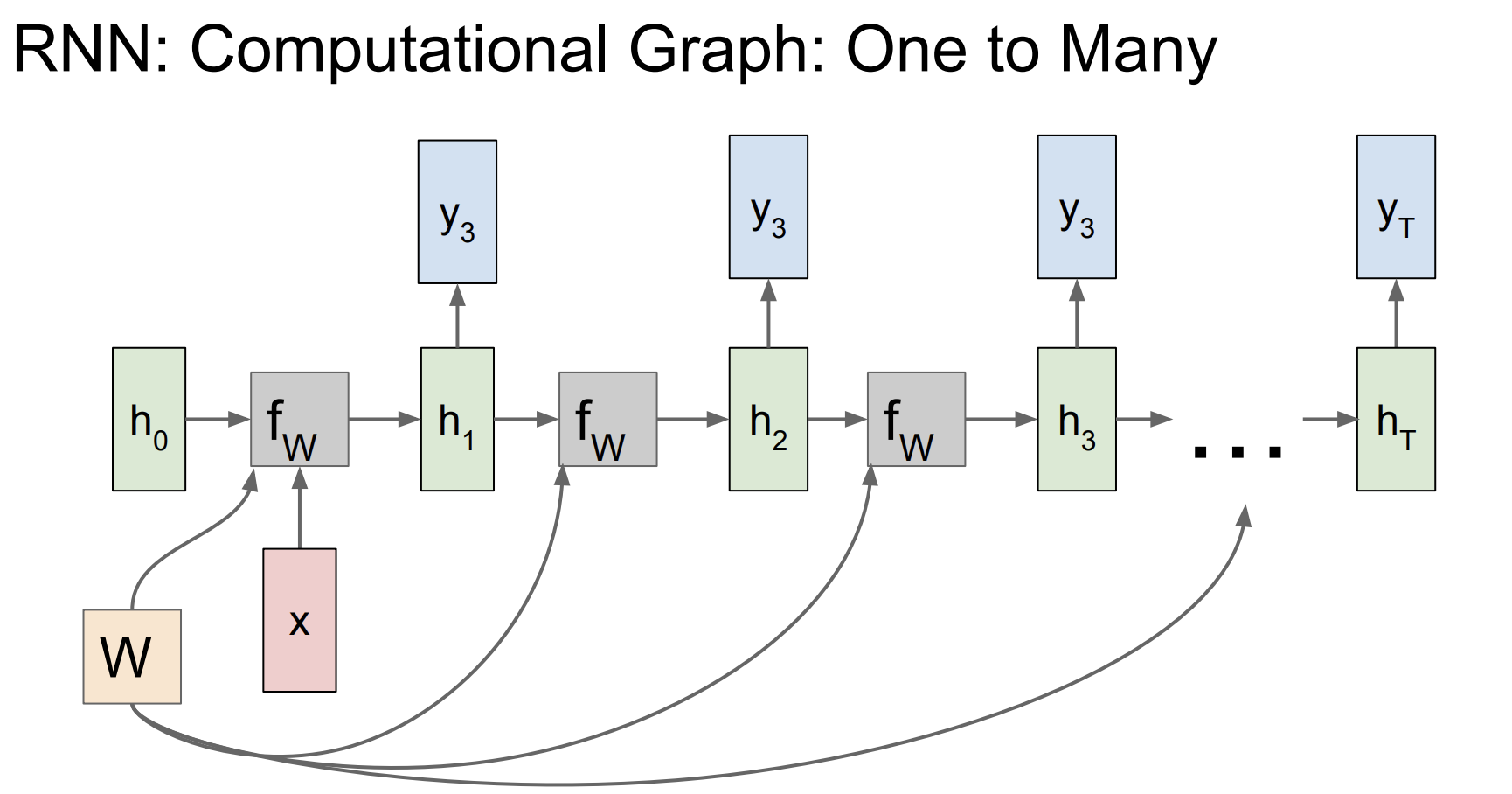
인풋이 fixed size이지만 가변적인 사이즈의 output을 가지는데, 이때 대부분의 fixed sized input은 모델의 initial hidden state를 초기화하는 용도로 쓰인다.
Sequence to Sequence
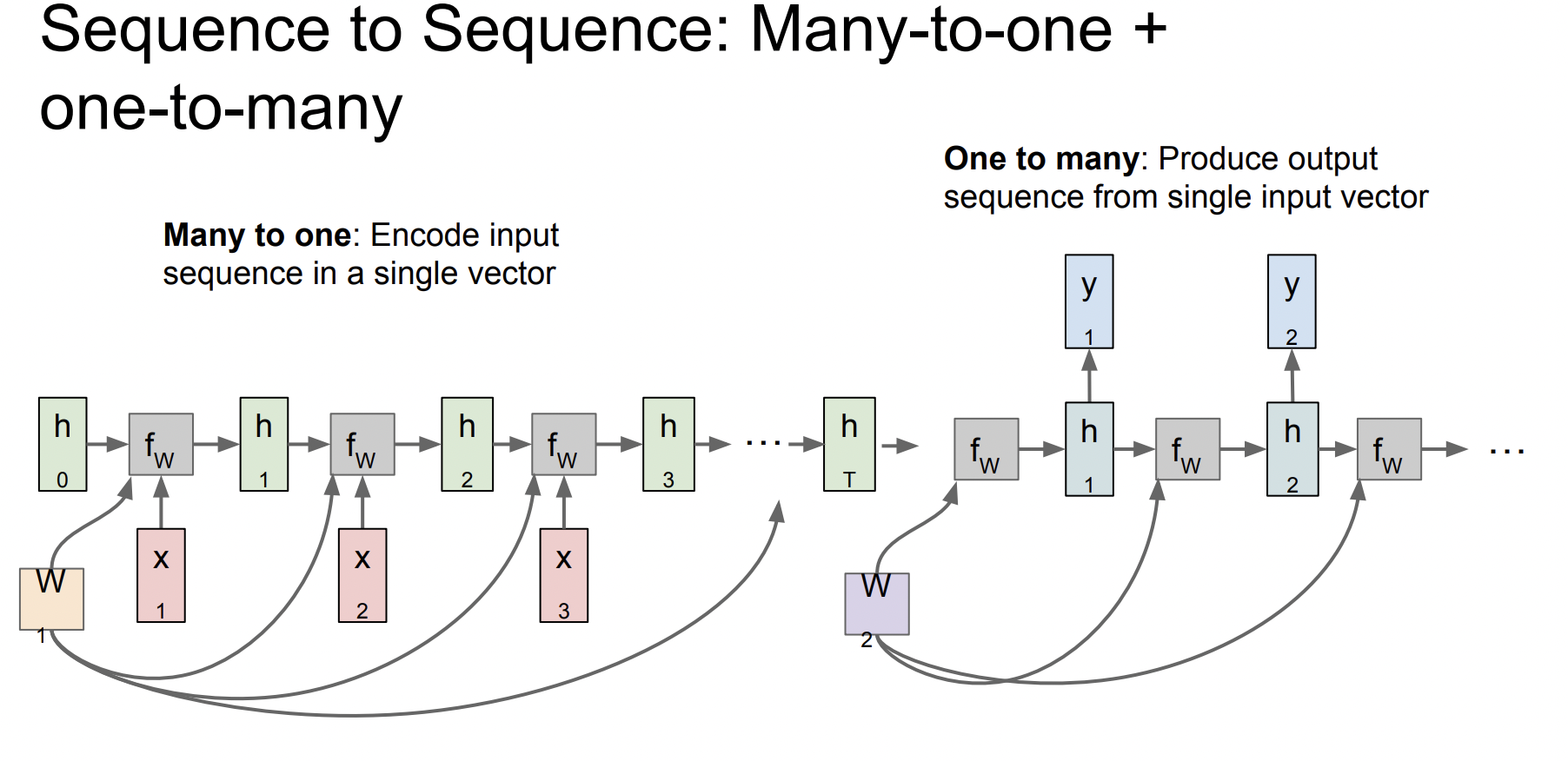
여기서 many to one과 one to many를 합쳐서 사용할 수도 있는데, many to one을 encoder로 사용하고 one to many를 decoder로 사용해서 기계 번역(machine translation)에 사용할 수 있다.
Truncated Backpropagation through time
RNN에서는 특별한 backpropagation 과정을 사용하는데, 우리가 일반적으로 사용하는 backpropagation 과정을 진행하면 전체 sequence를 가지고 진행해야 하기 때문에 시간도 매우 오래 걸리고 메모리 부족 문제도 발생한다.
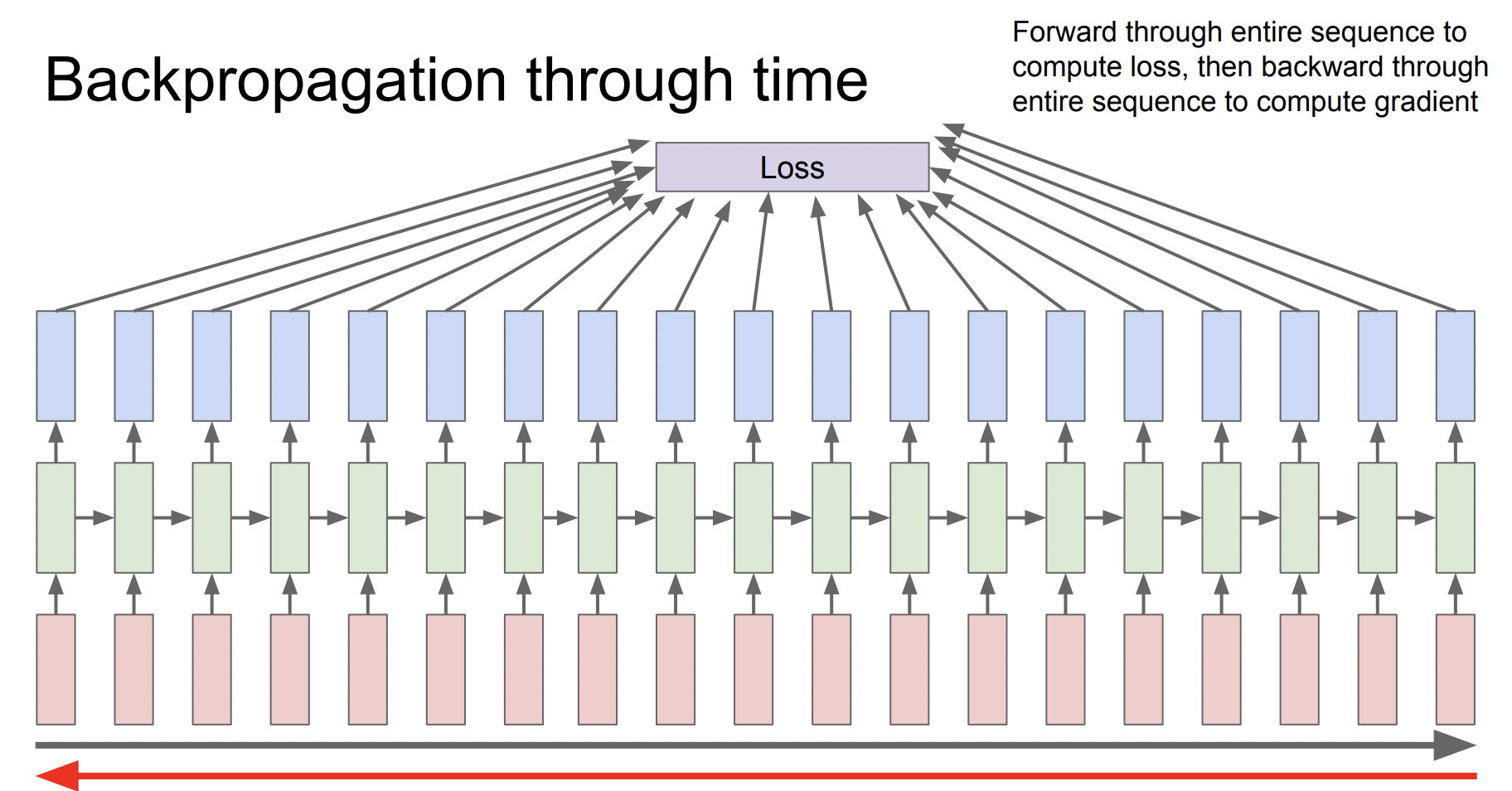
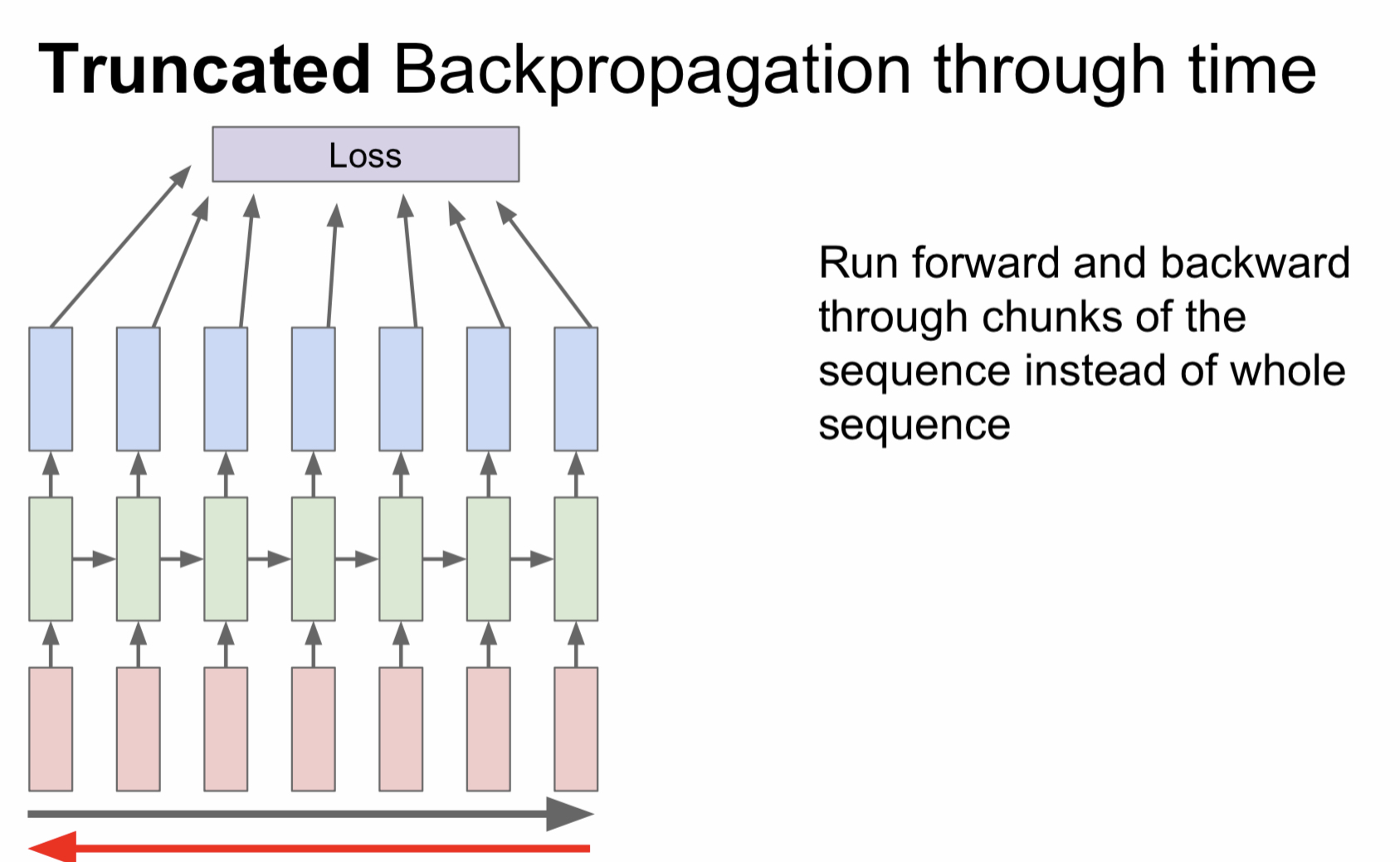
따라서 전체 데이터를 step마다 일정 단위로 나누어서 그 step에 대한 gradient만 계산하여 근사시키는 방법을 사용한다. sgd 방식을 sequence data 버전으로 진행한다고 생각하면 된다.
Multilayer RNNs
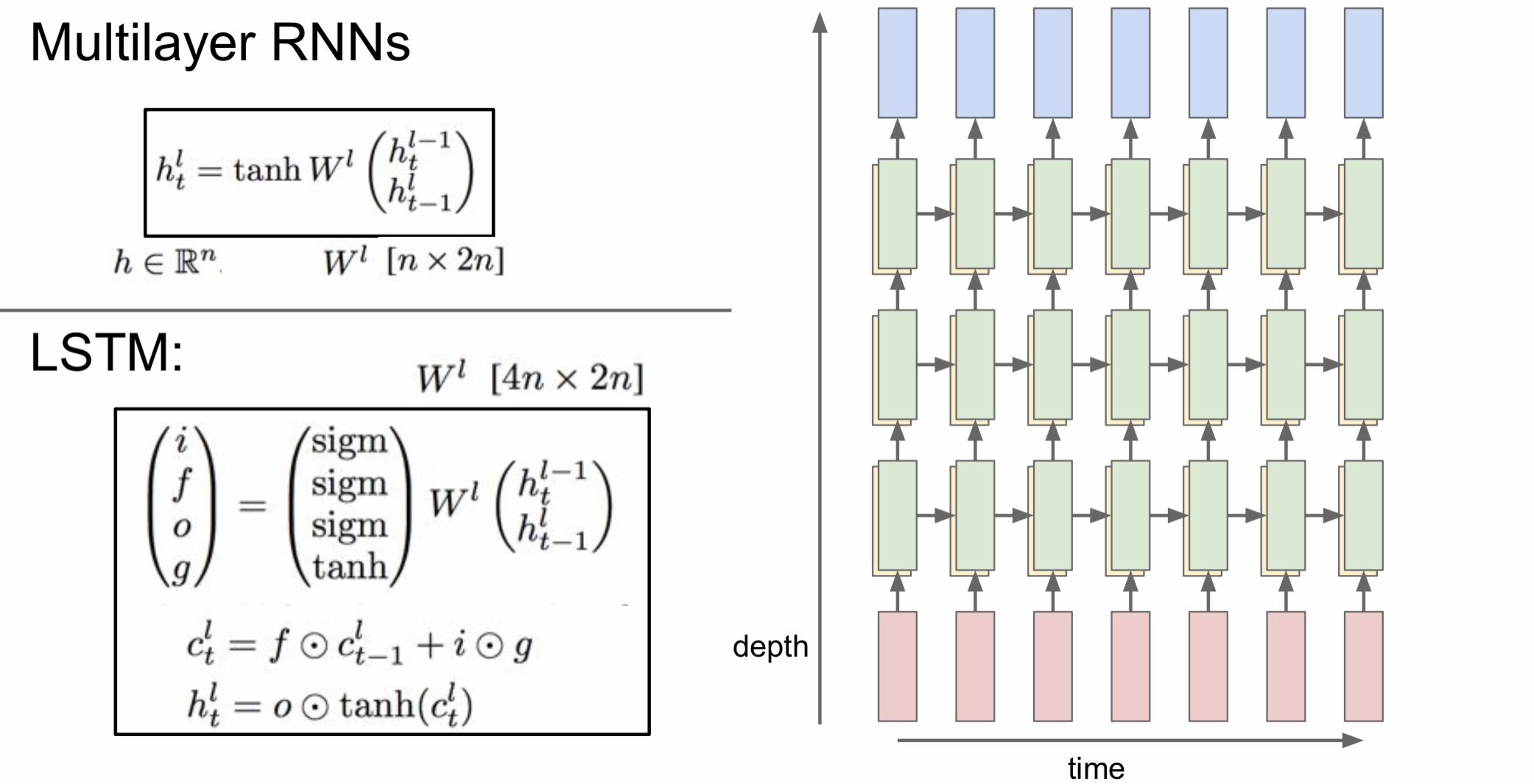
지금까지는 RNN layer를 하나만 사용해서 hidden state도 1개뿐이었다. 하지만 지금부터는 layer를 여러 개 쌓아서 사용한다. 여러 개의 layer를 쌓으면 다양한 문제에서 성능이 좋아지기 때문이다. 하지만 너무 많이 쌓지는 않고 보통 2~4 layer RNN을 사용한다.
Vanilla RNN Gradient Flow
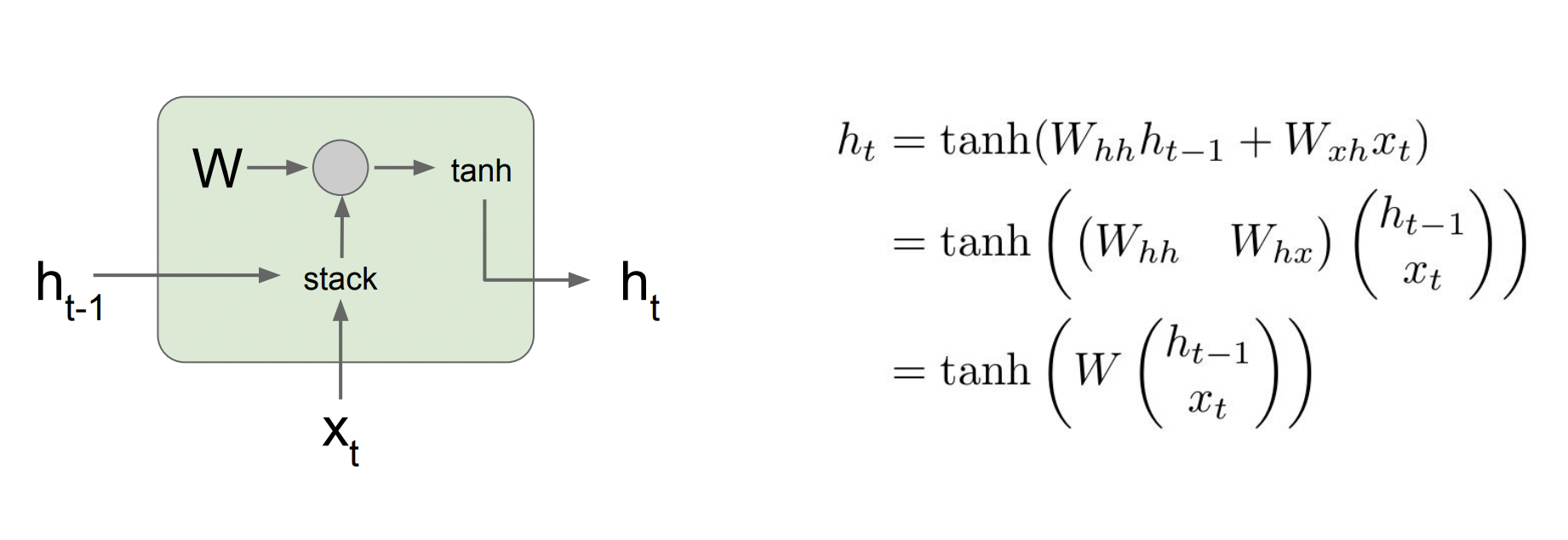
이 사진은 일반적인 RNN의 계산 과정이다. 현재 입력과 이전 입력을 쌓고 가중치 행렬인 W와 연산을 한 뒤 tanh 함수를 통과시킨다.
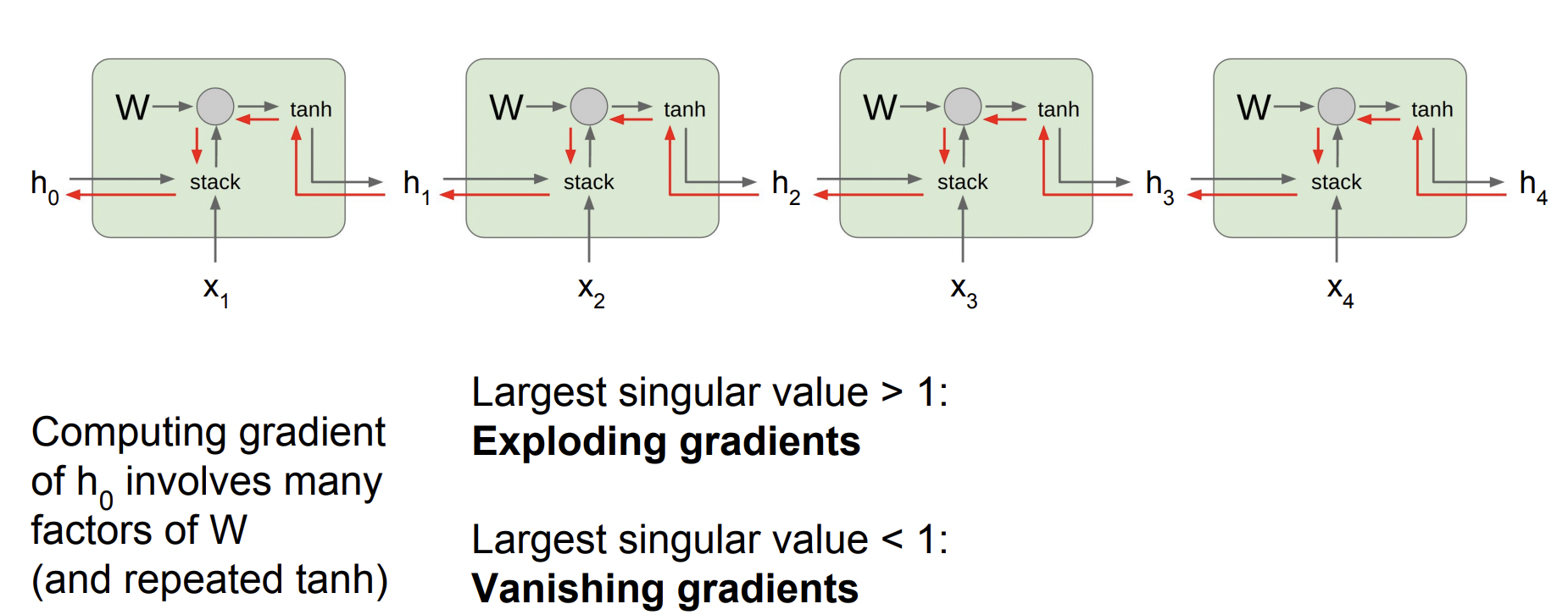
하지만 이렇게 계산한다면 문제점이 발생한다. 바로 backpropagation을 진행할 때 h0을 구하려면 모든 RNN cells를 거쳐야 한다는 것이다. 이렇게 값들을 계속해서 곱한다고 했을 때, 곱해지는 값이 1보다 크다면 값이 점점 커지고 1보다 작다면 점점 작아져서 0이 될 것이다.
- 곱해지는 값이 1보다 클 때 -> Exploding gradients
- 곱해지는 값이 1보다 작을 때 -> Vanishing gradients
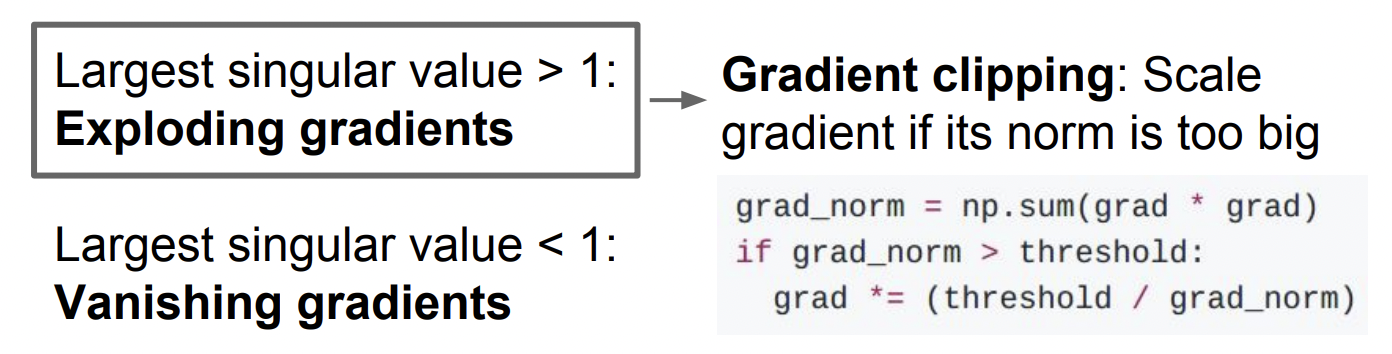
Exploding gradient를 막기 위해 사용하는 기법이 Gradient clipping이다. gradient의 L2 norm이 임계값보다 큰 경우 임계값을 넘지 못하도록 조정하는 방법이다.
하지만 Vanishing gradient를 다루려면 LSTM에 대해 알아야 한다.
Long Short Term Memory (LSTM)
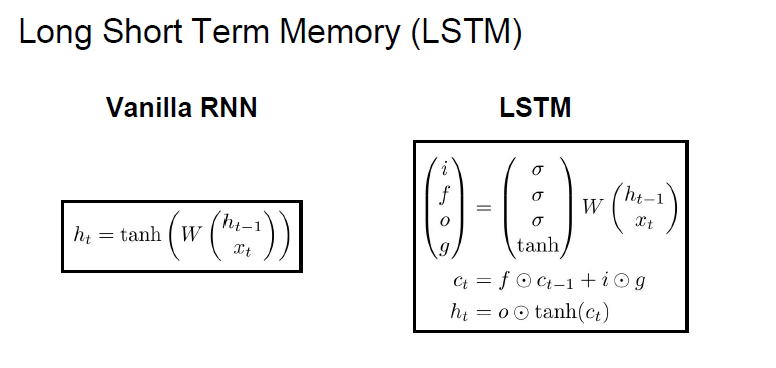
LSTM은 이러한 gradient 문제를 해결하기 위해 설계되었다.
Vanilla RNN과 비교하면 한 cell당 두 개의 hidden state가 있는 것이 특징이다. 바로 h_t와 c_t이다.
c_t는 cell state라고 하며 LSTM 외부에 노출되지 않는 변수이다.
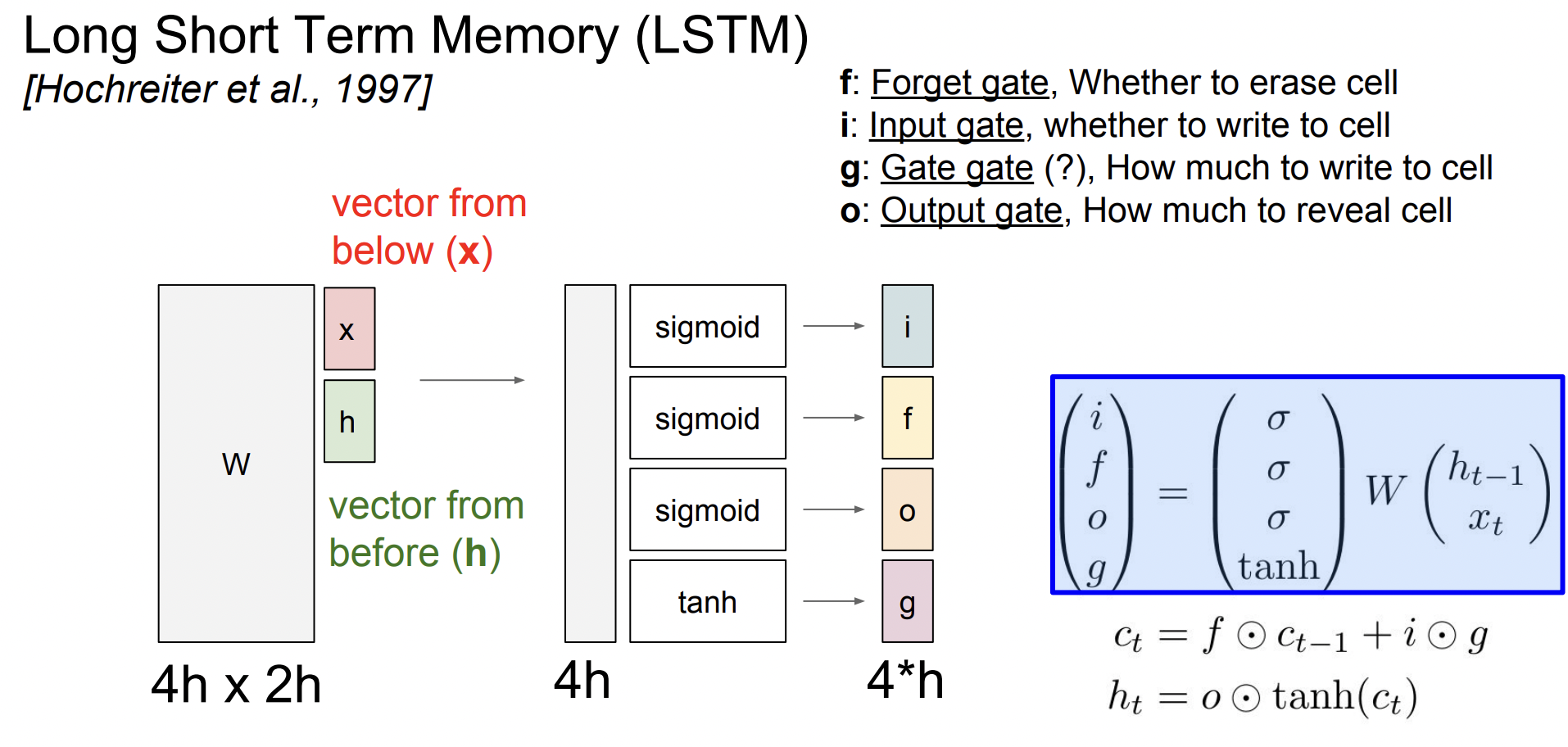
LSTM에서는 총 4개의 gate를 계산하게 된다.
- Forget gate : 0이면 이전 cell state를 잊음, 1이면 기억
- Input gate : 1이면 지금의 cell state를 사용, 0이면 미사용
- Gate gate : input sell을 얼마나 포함시킬 지 결정
- Output gate : hidden state를 계산할 때 cell state를 얼마나 노출시킬 지 결정
이때 Input gatei, Forget gatef, Output gateo는 sigmoid에서 나온 값이므로 [0,1] 의 값을 가지며 Gate gateg는 tanh에서 나온 값이므로 [-1,1] 의 값을 가진다.
Gradient Flow
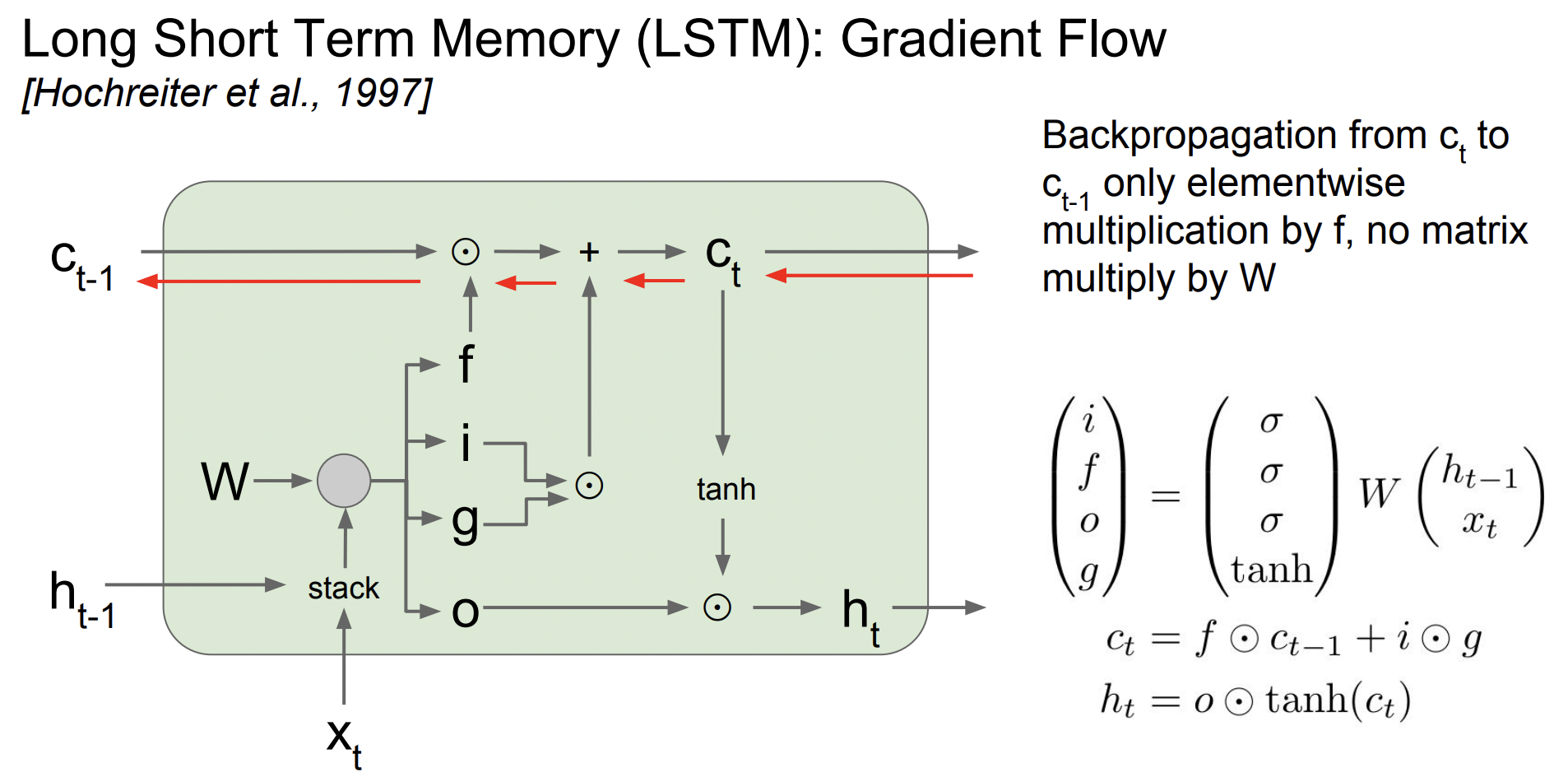
앞서 Vanilla RNN은 가중치 행렬 W가 계속해서 곱해지는 문제가 있었지만 LSTM에서는 조금 다르다.
gradient가 cell state에서 내려오는 upstream gradient와 forget gate의 element wise값이다. 즉 행렬곱 연산이 아니기 때문에 연산이 더 가벼워진다.
또한 매 스탭마다 다른 f값이 곱해지면서 exploding gradient와 vanishing gradient 문제를 해결할 수 있다.
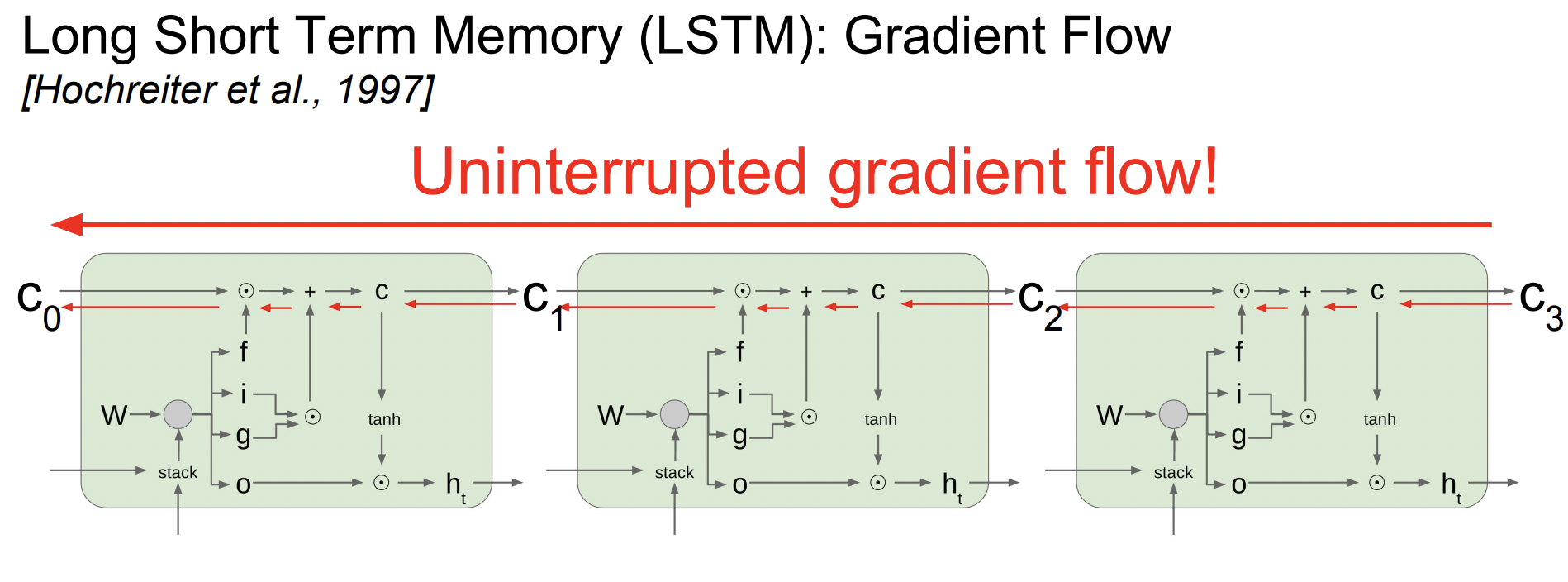
또한 RNN처럼 매 step마다 함수(tanh)를 거칠 필요 없이 단 한 번만 거치면 된다. 방해받지 않는 flow라고 할 수 있다.
