🔗강의 영상

목차

• Reinforcement Learning
• Markov Decision Processes
• Q - Learning
• Policy Gradients

강화 학습

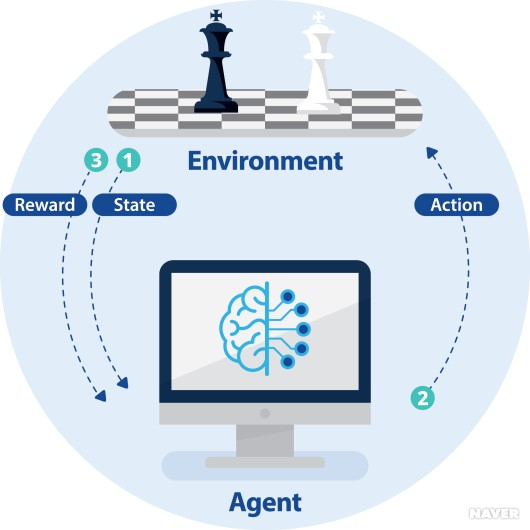
개념

agent와 environment와 상호작용하며 보상을 최대화하는 방향으로 학습하는 방법론.

• agent: action을 취할 수 있는 물체
• environment: agent와 상호작용하는 것으로 agent에게 적절한 state(상태)를 부여한다.

메커니즘

1. Environmet로 부터 Agent가 State를 부여받는다.
2. state를 받은 Agent가 어떠한 Action을 취한다.
3. 그 Action에 대해 Agent는 보상을 받는다.
4. 다음 State를 부여받는다.

Markov Decision Processes

개념

강화 학습의 기본적인 문제 설정을 위해 강화 학습을 수식화하는 것. agent가 action을 취하고 보상받는 과정을 모델링한다.

특징

Markov Property(마르코프 성질)을 가진다.

• Markov Property: 현재 상태가 과거의 모든 정보를 충분히 반영하며, 미래 상황은 오직 현재 상태와 선택된 액션에만 의존한다는 성질.

기호 정의

• S: state의 유한 집합
• A: agent가 취할 수 있는 action의 유한 집합
• R: state와 action에 대한 보상의 분포
• P: state와 action이 주어졌을 때, 다음 state에 대한 분포의 전이 확률(transition probability. s에서 s'로 이동할 확률)
• γ(감마): 현재 얻게 되는 보상이 미래에 얻게 될 보상보다 얼마나 중요한지 나타내는 값. (0~1)

사용 이유: 강화 학습을 MDP로 풀어 쓰는 이유: 누적 보상을 최대화 하는 π*를 찾기 위한 목적.

작동 원리

1. 시작 상태(time step=0): 환경에서 초기 상태 s0를 agent에게 준다.
2. agent는 현재 상태 s0에 기반하여 어떤 a0을 취하고, 보상 r0와 다음 상태인 s1을 agent에게 보내서 종료될 때까지 반복한다.
3. policy π: 각각의 state마다 action의 분포를 표현하는 함수. 각 state에서 어떤 action을 선택할지 정하는 것.

예시

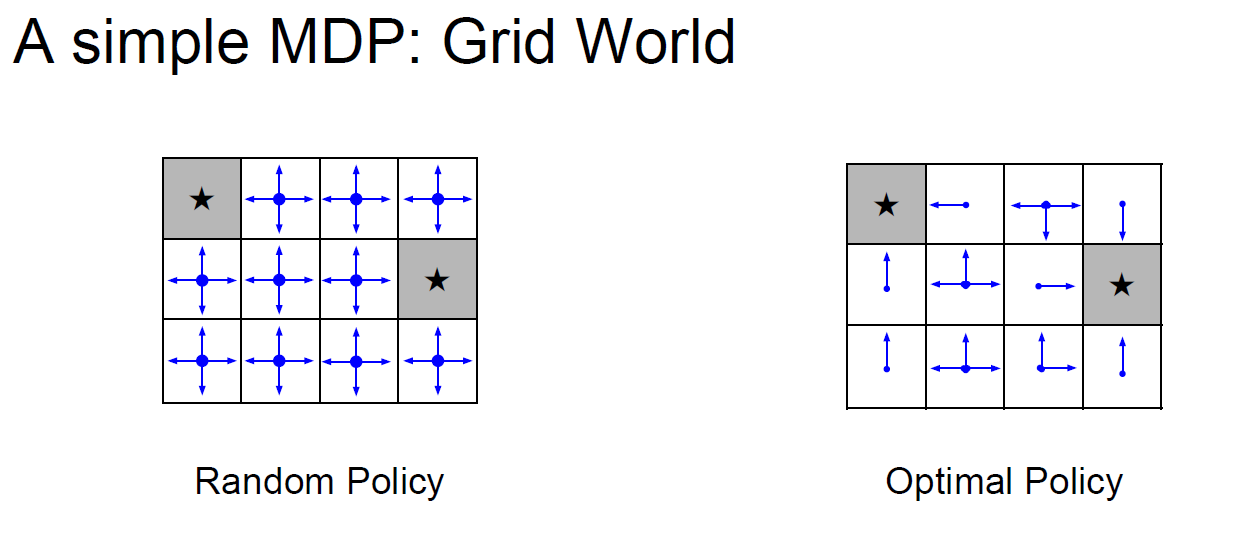
우리가 ★이 있는 쪽으로 가는 길찾기 문제를 푼다고 할 때, 최적의 정책 π가 존재한다면 길을 훨씬 수월하게 찾을 것이다. 보상을 최대화 할 수 있는 방법은 미래 내가 받을 보상들의 합이 최대가 되도록 하면 된다.

수식

1. optimal policy π*
   보상의 합을 최대화하는 π* 수식

   미래 보상들의 합에 대한 기대값을 최대화

   

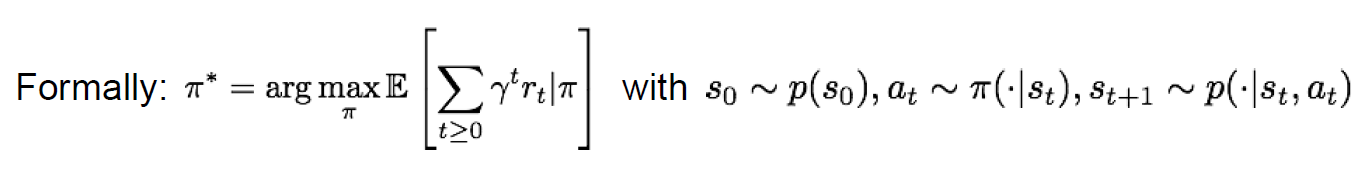
2. Value function
   어떤 상태 S와 정책 π가 주어졌을 때, 계산되는 누적 보상의 기댓값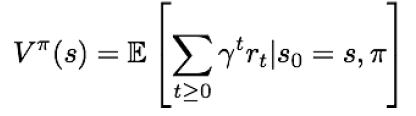

   

3. Q-Value funtion
   상태 s에서 어떤 행동을 해야 가장 좋은지 알려주는 함수

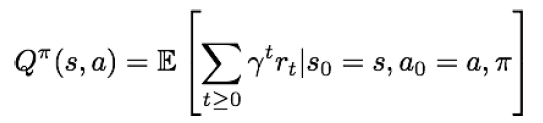
Bellman equation

현재 state의 가치와 다음 state의 가치 사이의 관계를 나타내는 수식.

개념

• 예를 들어 Q-value function인 Q이 있다고 가정하자. Q은 어떤 행동을 취했을 때 미래에 받을 보상의 최대치이기 때문에 최적의 경로를 도출할 수 있다. 즉, Q* 덕분에 어떤 상태에서든 최적의 보상을 받을 경로를 알기 때문에 s’에서도 최상의 action을 취할 수 있다.

• 하지만 여기서 scaleable하지 않다는 문제가 있다. 왜냐하면 모든 Q(s,a)에 대해 계산을 해야되는데 계산량이 너무 많다. 해결책으로 Neural Network을 이용하여 Q(s,a)을 계산 가능하도록 근사시킨다.

강화학습은 value iteration algorithm 방식을 사용함으로써 bellman equation을 반복적으로 돌려서 각 state의 value를 업데이트하고 최적의 policy를 찾는다.

Q - Learning

모델 없는 강화 학습 방법으로, 환경의 동작을 사전에 알지 못하고 상호작용을 통해 최적의 정책을 찾는다.

Deep Q-Learning(DQN)

DQN에서는 신경망(neural network)을 사용하여 Q(s,a)를 근사시킨다.

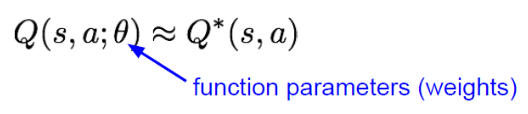
델타 파라미터는 neural network의 weights과 관련된 파라미터

Q(s,a) 행동-가치 함수(action-value function)

상태 s에서 행동 a를 취했을 때 얻을 수 있는 예상 미래 보상의 총합 함수.

네트워크 구조

Q - function은 Bellman equation을 만족해야한다.

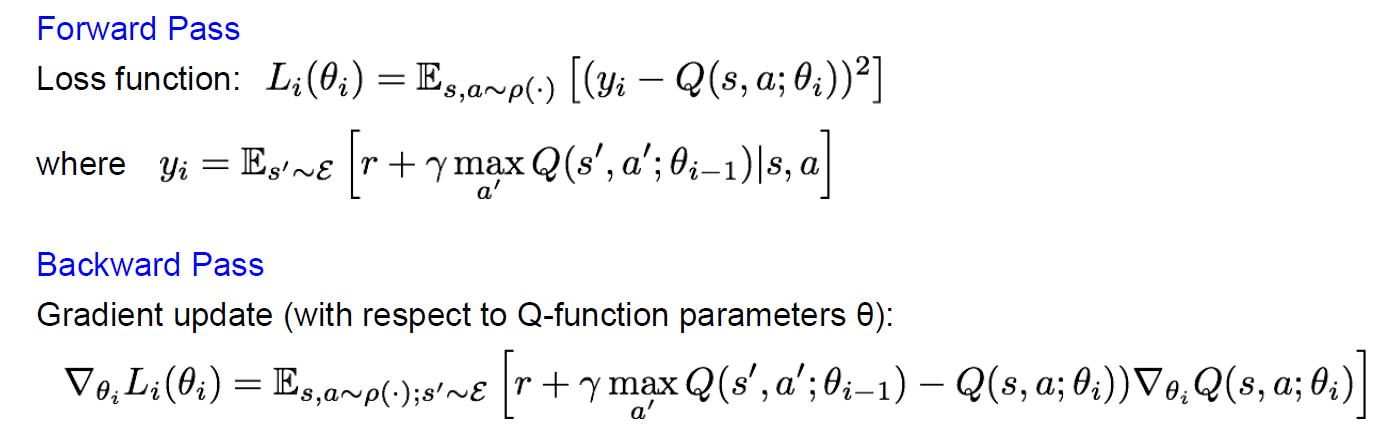
Forward Pass

손실 함수(Loss function) Li(θi): i번째 반복할 때의 손실 함수. 예측된 Q값(Q(s, a; θi))과 target 값(y_i) 사이의 차이를 제곱 오차로 얼마나 차이가 나는지 측정한다.

yi: target 값. Bellman equation을 만족하는 정답 방정식. 현재 상태와 행동에 대한 보상(r)과 다음 상태(s')에서 가능한 모든 행동 중 최대 Q값을 γ(감가율)로 조정하여 더한 것.

Es,a~p(ㆍ): 정책 p에 따라 선택된 모든 가능한 상태 s와 행동 a 조합에 대한 (괄호 안의) 기대값

Backward Pass

∇θiLi(θi): i번째 반복 때의 손실 함수에 대한 gradient. 경사 하강법 같은 최적화 알고리즘을 사용하여 loss값에 대하여 θ를 계속 update한다.

예시: Atrari Game

atrari game에서 점수를 얻는 방향으로 강화 학습 시키는 q-learning을 진행했다. 벽돌깨기 같은 게임의 학습을 거듭할 수록 실수하지 않고 득점한다.

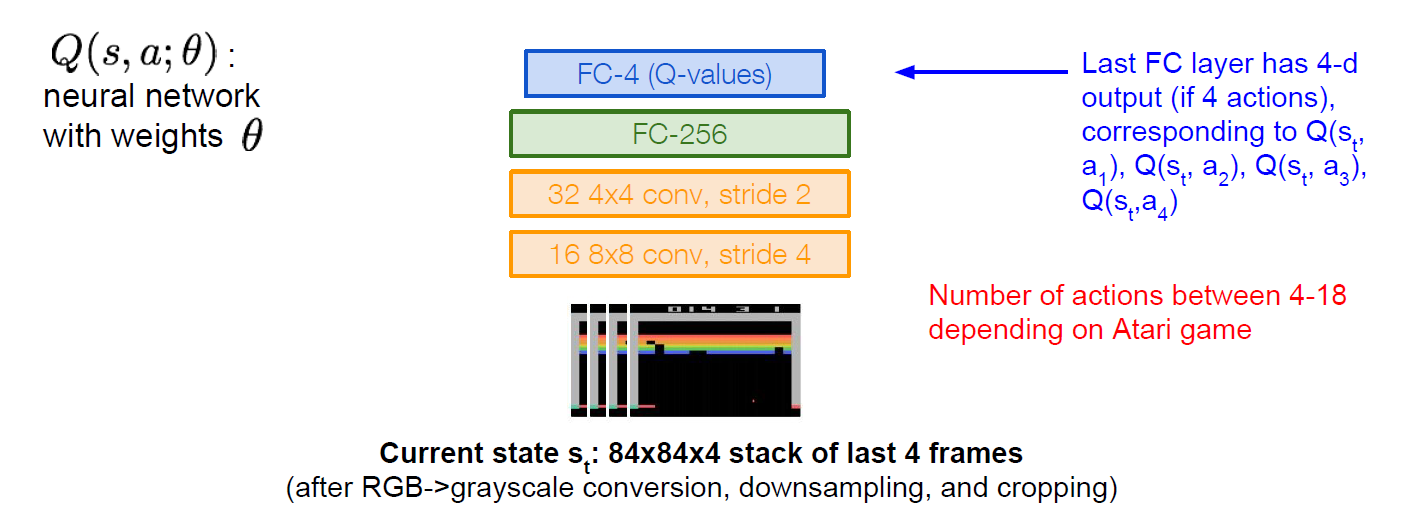
입력: 게임 화면을 84 * 84 크기로 만든 다음 4프레임 정도를 누적시켜 넣어준다. 이 네트워크 구조의 장점은 한 번의 forward pass만으로 모든 함수에 대한 q-value 값을 계산할 수 있다는 것.

Q - network의 training: Experience Replay

학습이 진행되면서 얻은 새로운 experience를 바로 학습에 사용하지 않고, replay memory에 저장한 후, mini batch 형태로 random sampling하여 신경망을 학습한다.

이렇게 학습하는 이유: data간의 상관관계가 생기면 학습이 효율적이지 못하기 때문에, 가중치 값을 update하는데 여러 번 갱신시킬 수 있기 때문에.

단점

모든 state에 대해 Q-value값이 존재해야 해서 function이 복잡해진다. 위 벽돌깨기 게임 같은 경우는 state가 4 방향으로 움직이며 변경되는 것 뿐인데, 어떤 로봇이 물체를 잡는 것과 같은 행동을 강화 학습으로 풀려면 state 차원은 매우 높아진다.

Policy Gradients

상태에 따른 Q - value값들을 학습시키는 것이 아니라 정책(Policy) 자체를 직접 학습시켜 최적화하는 방법

J(θ): 미래에 받을 보상을 누적으로 하여 기댓값을 나타낸 함수

목표: J(θ)를 최대화시키는 θ*를 찾는 것.

Reinforce Algorithm

메커니즘

에피소드가 끝날 때까지 에이전트가 경험을 쌓은 후, 각 스텝에서 얻은 보상을 사용하여 정책(policy)을 update한다. 양의 보상을 가져다주는 행동의 확률을 증가시키고, 음의 보상을 가져다주는 행동의 확률을 감소시키는 메커니즘. 각 에피소드에서 실행된 행동들에 대한 gradient를 계산하고, 이를 사용하여 policy parameter를 update한다.

수식

특정 Policy 인 θ가 정해지면 state, action과 그 에 대한 reward가 나올것이다. 이를 흔적(trajectory)이라고 하고 object function은 흔적을 기반으로 reward를 측정하게된다.

그리고 기대값은 보통 확률*그 확률일 때의 값으로 표현된다.

• r(τ): 해당 경로 τ에서 얻는 총 보상.
• r(τ)p(τ;θ): 특정 경로 τ가 발생할 확률 * 그 경로에서 얻게 되는 보상. (아직 잘 이해x)
• r(τ)p(τ;θ)값을 적분한 이유: 연속적인 상태와 행동 공간에 대해 다루고 있기 때문.
  

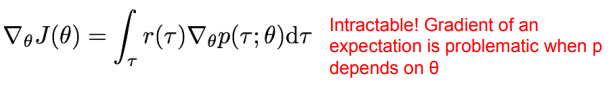
위 사진- object function J(θ)의 gradient를 계산하는 수식

위 식에서 보상 r과 확률밀도함수 p가 모두 경로 τ에 의존하며, p는 추가적으로 θ에도 의존하기 때문에 계산이 매우 복잡해진다. (intractable하다) 따라서 수식을 조금 변경해준다.

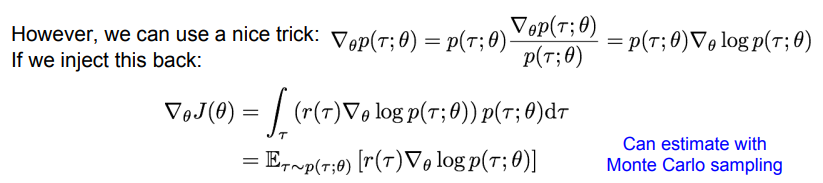
위 사진은 score function(로그-확률을 이용한 미분 기법)방법을 이용하여 J(θ)의 gradient를 계산하는 과정이다.

• 첫 번째 수식: ∇θp(τ;θ) = p(τ;θ) ∇θlog p(τ;θ): log 함수의 미분 성질과 chain rule을 이용.
  • log 함수의 미분 성질: y = log(x))를 x에 대해 미분하면, dy/dx = 1/x 가 된다. 확률밀도함수 p에 log를 취하면 미분이 용이해지는 성질
  • chain rule: f(g(x)))' = f'(g(x)) * g'(x) (4강에서 언급됨)
  • ∇θlog p(τ;θ): log 확률밀도함수 p를 파라미터 θ로 미분한 것.
• 두 번째 수식: 첫 번째 식에서 구한 ∇θp(τ;θ)을 원래 gradient 식(∇θJ(θ)=∫r(τ)∇θp(τ;θ) dτ)에 대입한다.
• 세 번째 수식: 기대값(E~)은 모든 가능한 경로 τ에 대해 평균을 알아야 하지만 실제로 모든 가능성을 고려하는 것은 너무 어려워서 계산할 수 없다. 따라서 강화학습에서는 보통 기댓값을 계산할 때 사용하는 Monte Carlo sampling을 사용한다.
  • Monte Carlo sampling: 현재 정책에서 생성된 경로들만 가지고 평균치를 추정하는 방법
• 수식의 결론
  • 구체적인 Q-value값은 몰라도 정책 자체J(θ)의 gradient를 구해 최적의 정책을 찾을 수는 있다.
  • J(θ)를 기댓값의 형식으로 변환했다. (??)

전이 확률(transition probabilities)없이 policy gradient를 추정하는 방법

5번 식에서 p(τ;θ)를 계산하려면 전이 확률을 알아야 하지만 p7번에서 기대값 형태로 유도한 policy gradient 추정 식에서 알 수 있든 전이 확률이 필요하지 않다. 미분을 하면 0이 된다.

어떤 경로의 r(τ) (특정 경로 τ에 대한 보상)이 크면 action들의 확률을 높이고, 낮으면 낮춘다. 구체적으로 어떤 행동이 좋은지 파악하고 그 행동에 대한 우도(likehood)를 높이고 싶지만 기대값 계산에 의해 모든 값이 평균화된다. 충분히 많은 샘플링을 한다면 큰 수의 법칙에 따라 gradient를 이용해서 최적의 parameter 값을 찾아낼 수 있지만, 그렇게 된다면 샘플의 분산이 너무 높다는 문제가 발생한다. 해당 경로에서 모든 action이 좋았다는 보장을 할 수 없다는 불확실성을 가진다. 따라서 단순히 보상이 양수였다는 것보다는 상대적으로 좋고 나쁨에 대한 판단을 할 수 있도록 수식을 변경한다.

Variance reduction 3가지 방법

1. 해당 state로부터 받을 미래 보상만 고려하여 어떤 행동을 취할 확률을 키운다.
2. 지연된 보상에 의해 할인률을 적용한다.

3. Baseline

• 보상의 기준을 0으로 두는 게 아니라 설정한 임의의 baseline을 중심으로 보상이 baseline보다 크면 양수, 아니면 음수로 처리하는 방법.
  

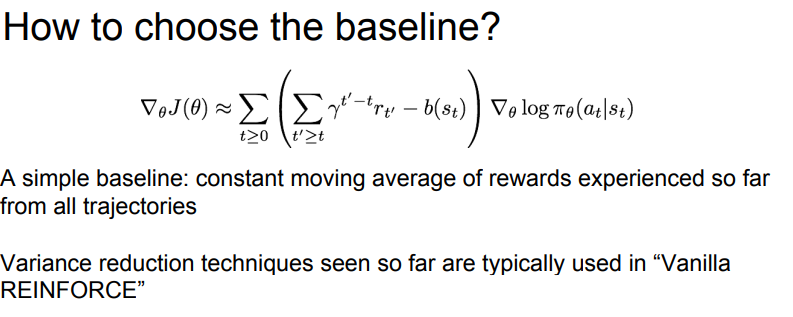
사진 - 기본 baseline 활용 수식

vanilla reinforce

할인율을 적용하여 미래에 받을 보상을 누적시키고 simple baseline을 추가하는 방식.

Actor-Critic Algorithm

Actor와 Critic 두 가지 구성 요소가 서로 협력하여 agent의 최적 행동을 학습하는 방식.

• Actor: action을 결정하는 policy를 학습한다. 확률적 정책 혹은 Deterministic 정책
• Critic: Actor의 행동을 평가한다. agent가 특정 state에서 기대되는 미래 보상을 예측하는 가치함수를 학습한다. v-value function은 state만을 고려한 가치를 예측하며, q-value function은 state와 특정 action을 고려한 가치를 예측한다.
• 작동 방식:
  1. θ,ϕ를 초기화 시킨다.
  2. 현재의 policy를 기반으로 M개의 경로를 샘플링한다.
  3. Gradient를 계산한다. 각 경로마다 보상 함수를 계산하고 이용한다.
  4. 보상함수를 이용해서 gradient estimator를 계산하고 이를 전부 누적시킨다.
  5. ϕ를 학습시키기 위해 가치 함수를 학습시킨다. 가치 함수는 보상 함수와 동치이므로, 가치 함수가 벨만 방정식(Bellman equation)에 근접하도록 학습시킨다.
  6. 앞선 단계를 계속 반복한다.

RAM(Recurrent Attention Model)

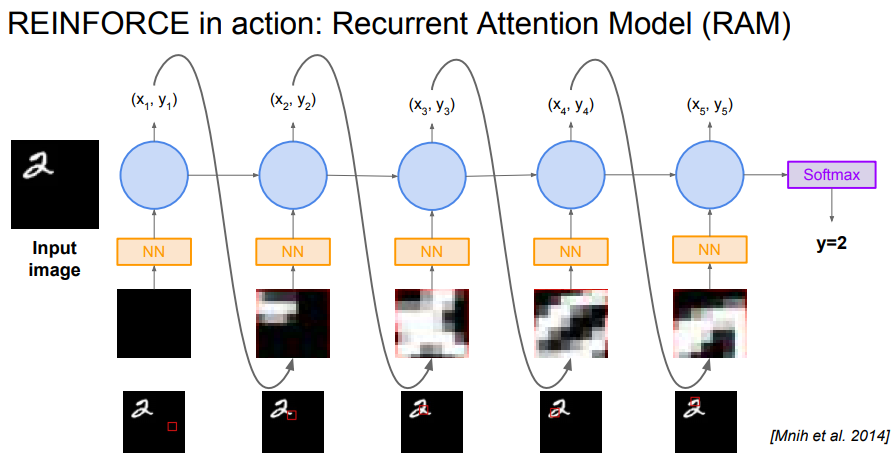
강화학습에 attention을 활용하면 이미지를 지엽적으로 보게 되어 비용을 아낄 수 있다