엔트로피, 크로스 엔트로피, negative log likelihood

실무만 하다 보니 기초를 등한시하게 되는 것 같아 다시 복기하는 겸 정리한다.

• 엔트로피: 정보를 표현하는데 사용되는 최소한의 정보량
  수식: $\sum_{i}^{} p_{i}*(-logp_{i})$
  

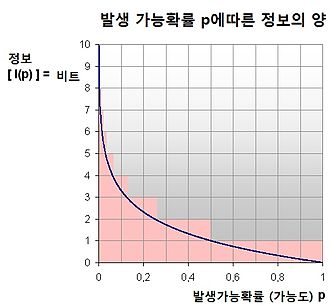
예시

• 자주 쓰이는 값이 많은 정보로 표현되면 안됨. 그렇게 되면 비효율성이 커짐.
• 반대로 발생 빈도가 낮은 값이 많은 정보로 표현되야 함. 그렇게 되야 효율성이 커짐.

크로스 엔트로피: $\sum_{i}^{} p_{i}*(-logq_{i})$

• q는 예측한 확률이다.
• 따라서 q가 위의 p에 근접하도록 예측하여야 비효율적인 것에서 효율적인 방향으로 되는 것이다.
• 이러한 관점에서 우리는 딥러닝 모델을 생각할 수 있다.
• 딥러닝 모델에서도 위와 같은 크로스 엔트로피를 loss function으로 사용하는데 의미는 다음과 같다고 생각하면 된다.

• 예시를 한 번 생각을 해보자. 우리가 해결해야 하는 multiclass classification 문제가 있다. multiclass classification 문제에서는 일반적으로 예측해야 하는 값들을 확률적으로 나타낸다. softmax 함수는 아래와 같다.
  수식: $p(y_{i}|x_{i};\Theta ) = \frac{exp\{f(x_{i})\}}{\sum_{j}exp\{f(x_j)\}}$

• 위의 수식의 핵심을 말하자면 분자의 각각의 값을 합하면 1이 된다.(시그마 기호에 의해) $\theta$에 대하여 $x_i$가 주어진 것에 대한 output $y_i$의 확률값이다. 이는 $f$함수에 따라서 나오는 값이다. 따라서 $f$의 요소값을 높인다는 말은 우도를 높인다는 말이고, 이는 $x_i$에 따라 정답 데이터 분포에 가까운 $y_i$를 뽑아낸다고 생각하면 된다.

• 따라서 위의 수식의 $q_i$자리에 $p(y_{i}|x_{i};\Theta )$을 넣고, $p_i$에 정답 데이터 분포인 $p(y_{i}|x_{i})$를 넣어서 정리하면 $-\sum_xP(y|x)logP(y|x;\theta)$가 되고, 이가 최소가 되게 하는 loss function의 의미는 결국, 예측한 확률의 값이 정답의 확률에 가까운 값이 되도록 한다는 것이다.

• 이를 엔트로피 관점에서 보면 최소한의 정보량에 가깝도록 모델을 학습하면서 파라미터를 추정하는 것이다.

• 이러한 형태를 우리는 negative log likelihood라고 한다.