프로그래머스 - 택배 배달과 수거하기

문제

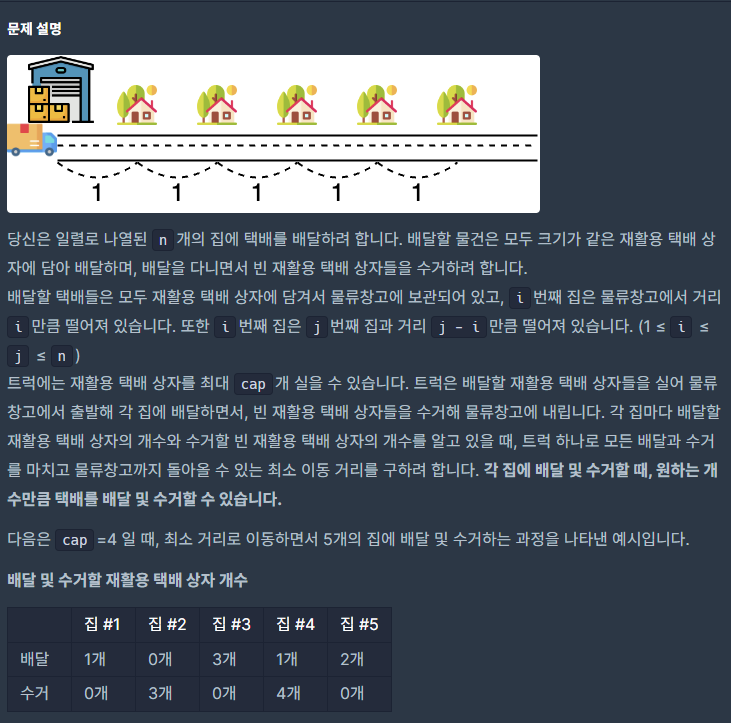
• 문제는 위와 같이 정의된다.
• solution 함수는 4가지 parameter를 인자로 받는데, 각각의 인자는 다음과 같다.
  • cap : 트럭에 담을 수 있는 최대 택배 상자 수
  • n : 배달 또는 수거를 할 수 있는 집의 개수
  • deliveries : 배달해야 하는 집에 대한 array
  • pickups : 수거해야 하는 집에 대한 array

해결 예시

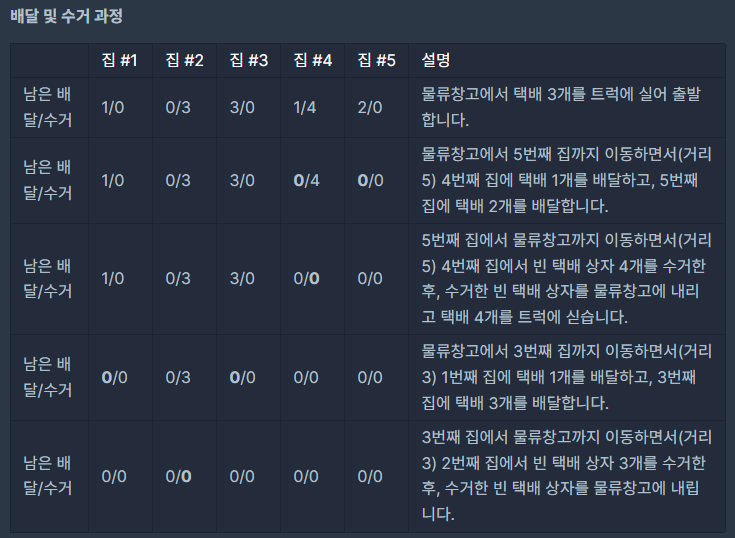
• 위는 프로그래머스에서 제시한 해결방법이다. 또한 직접 코딩 테스트 문제를 풀고자 했을 때 또다른 예시가 하나 더 있는데, 그것들을 분석해본 결과, 거리가 먼 집부터 먼저 배달 또는 수거를 하는 것이 가장 효율적인 방법으로 생각된다. 따라서 다음과 같은 방식으로 코드를 구성해야 한다.
  • cap만큼의 최대 택배를 싣고 배달을 출발한다.
  • 가장 거리가 먼 집에 배달을 다 할 것을 고려하면서 배달을 한다. 예를 들어, 위와 같은 상황일 때, 집 #5 에 배달해야 할 물품 개수는 2이고, 집 #4에 배달해야 할 물품 개수는 1이다. 두 집에 배달해야 할 물품의 총 개수는 3이고, cap은 4이므로 아직 하나를 더 배달할 수 있다. 그렇기 때문에 집 #3에도 배달 물건을 1개 배달할 생각으로 배달을 진행한다.
  • 배달을 다 진행한 후에는 가장 먼 거리부터 cap만큼 수거 물품을 실어서 돌아온다.

code

def solution(cap, n, deliveries, pickups):
    answer = -1

    total_deliveries = sum(deliveries)
    total_pickups = sum(pickups)
    dist = 0
    d_idx = n - 1
    p_idx = n - 1
    while True:
        only_pickups = False # 픽업만 할 수도 있는 경우를 고려한 변수
        # 배달이나 수거할 물건이 남았는지에 대한 체크
        if total_deliveries <= 0:
            if total_pickups <= 0:
                break
            else:
                only_pickups = True

        deliveries_cnt = 0
        pickups_cnt = 0
        stop_loc = []
        
        if not only_pickups:
        	# 배달할 물건을 먼 거리부터 배달
            for i in range(d_idx, -1, -1):
                if deliveries[i] != 0:
                    d_idx = i
                    stop_loc.append(i+1)
                    if deliveries_cnt + deliveries[i] >= cap:
                        deliveries[i] -= (cap - deliveries_cnt)
                        deliveries_cnt = cap
                        break
                    else:
                        deliveries_cnt += deliveries[i]
                        deliveries[i] = 0
            total_deliveries -= deliveries_cnt
            
        # 수거할 물건을 먼 거리부터 수거
        for i in range(p_idx, -1, -1):
            if pickups[i] != 0:
                p_idx = i
                stop_loc.append(i + 1)
                if pickups_cnt + pickups[i] >= cap:
                    pickups[i] -= (cap - pickups_cnt)
                    pickups_cnt = cap
                    break
                else:
                    pickups_cnt += pickups[i]
                    pickups[i] = 0
        total_pickups -= pickups_cnt
        
        # stop_loc에 담겨 있는 값 중 가장 먼 거리를 기반으로 배달/수거 거리 계산
        if len(stop_loc) != 0:
            dist += 2 * max(stop_loc)
            
    answer = dist
    return answer
    

고려해야 할 점

• 배달보다 수거해야 할 총 개수가 많을 경우, 배달은 안 하지만 수거만 할 case가 존재가능함.
• 탐색을 최대한 적게 할 수 있는 방법을 고려해야 함.
• 탐색하다가 cap을 다 채워버려서 탐색 도중 중단 되는 case에 대한 고려를 해야함.
• 탐색하고 난 곳은 다시 탐색을 안 할 수 있는 방법들을 고려해야 함.