
ML, Deep Learning 연산을 이해하기 위해선 선형대수, 행렬미분, 확률에 대해 알아야만 한다.
행렬과 확률이야 뭐.. 선형대수에 대해 내용을 이번 기회에 제대로 한번 정리해보고자 한다.
✅ Matrix
python에서 벡터, 행렬 표현하는 방법은 다음과 같다. (numpy 활용)
->import numpy as np # 1차원 x = np.array([10.5, 5.2, 3.25, 8.0]) # 2차원 column 기준 확장 x_2dim = np.expand_dims(x, axis=1) # column vector j = 1 x[:, j] # row vector i = 1 x[1, :] # Norms A = np.array([ [100, 200, 300], [ 10, 20, 30], [ 1, 2, 3], ]) import numpy.linalg as LA LA.norm(A) # 376.0505285197722 np.trace(A.T.dot(A))**0.5 # 376.0505285197722행렬의 종류는 다음과 같다.
- Square matrix : 행, 열 개수 동일
- Upper triangular matrix : square matrix이며 주대각선 아래 원소 모두 0
- Lower triangular matrix : square matrix이며 주대각선 위 원소 모두 0
- Diagonal matrix : square matrix, 주대각선 제외 모두 0
- Identity matrix : diagnonal matrix 이며 주대각선 원소 모두 1, I로 표시
-> np.diag([])로 diagonal matrix 생성 가능- Symmetic matrix : A = A.T 인 행렬, A = -A.T 인 경우 anti-symmetic
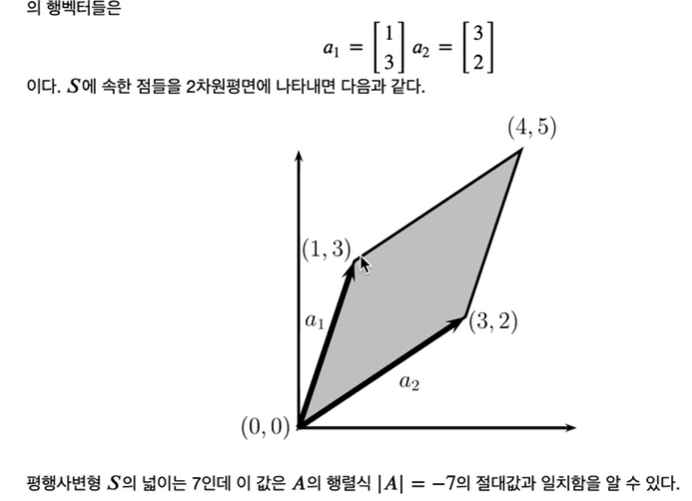
|det(A)| = 집합 S의 부피
- Quadratic Forms
square matrix와 벡터가 주어졌을 때 scalar 값 x.T AX를 이차 형식이라 부른다.
- Gram matrix : 임의의 행렬 A가 주어졌을 때, G = A.TA이고, G는 항상 positive semi-definite이다. 만약 m>=n이고, A가 full rank이면, G는 positive definite이다.
✅ Linear Algebra
✨ Linear Independence & Rank
벡터들의 집합에 속한 어떠한 벡터도 나머지 벡터들의 선형조합으로 나타낼 수 없을 때 이 집합을 선형독립이라 부른다. 역으로 어떠한 벡터가 나머지 벡터들의 선형 조합으로 나타내질 수 있다면, 이 집합을 선형 종속이라 부른다.
- Column Rank : 행렬 내 열들의 subset 중 가장 큰 선형독립인 집합의 크기
- Row Rank : 행렬 내 행들의 subset 중 가장 큰 선형독립인 집합의 크기
-> 모든 matrix의 column rank와 row rank는 동일하고 rank(A)로 표시한다.
행렬이 full rank이면 해당 행렬은 Invertible (non-singular)
이외에도 뭐 고유값, 고유벡터에 대한 설명이라든지, 행렬미분 등 주요 설명들에 대해서는 추가로 정리하는 부분은 생략.
eigenvector, eigenvalue가 물론 주성분분석인 PCA에서 쓰인다는 점(autoencoder 형태), least square 등 최적화 관련으로 주요한 부분이 존재하지만, 학부시절 강의와 네이버 부캠강의로 이전에 학습했기에 넘어가고자 한다.!
-> 🎈 why PCA ?
: (m개의 feature들을 n개로 차원으로 축소하는 개념이 PCA인데 이를 행렬로 보면, m개로 이루어진 벡터의 집합에서 각 벡터를 n차원으로 투영시킨 함수(인코딩), 이를 다시 m차원으로 회복하는 함수 (디코딩) 로 볼 수 있다.여러 행렬들을 살펴보고 학습하다보면 상당히 많은 명제들이 존재하는데, 이를 암기하기 보단 이해하면서 받아들이게 된다면 데이터를 바라보는 관점 역시 수학적으로 바라보게 되어 결국 모델 학습에 있어 더 나은 performance를 측정할 수 있게 된다.
결론 : 절대 암기하지 말자. 이해하는 습관을 기르자.
✅ ML practice
어제에 이어 delivery time 예측 모델 개발 프로젝트 작성.
현 상황.
- 결측치 있는 행의 경우 해당 row 모두 제거 -> train : 158587 // test : 17661 split ratio (0.11) -> fixed.
- 인코딩(음식점 종류 - 범주형), 스케일링 과정 이후 -> 모델링 필요.
🎈 Encoding
CATBoost가 아닌 이상 범주형 변수는 string 형이기에 모델이 인식할 수 없고, 이를 변환하는 작업을 반드시 거쳐야 한다. 범주형 변수는 순서가 있냐 없냐로 나뉘며 다음으로 나뉜다.
- Nominal : 성별, 혈액형과 같이 값이 달라짐에 따라 좋거나 나쁘지 않음. (순서 x)
- Ordinal : 학점, 만족도 조사 등과 같이 값 변화에 따라 좋거나 나쁜 경우 (순서 O)
-> 주어진 범주형 변수는 Nominal 형태.인코딩 종류는 다음과 같다.
1. Label Encoding : 알파벳 순서에 따라 문자형 데이터를 unique한 숫자로 변경.
-> Ordinal 변수에 적합
2. OneHotEncoding : 0,1로 구성된 벡터로 표현하는 기법. 단, 범주가 너무 많은 경우 데이터의 cardinality 증가시켜 모델 성능 저하 가능.따라서 onehotencoding을 사용해 해결하려했으나, 다음과 같은 이슈 발견
이처럼 범주가 상이한 경우, 모델 학습에 문제가 발생하게 되고 train으로 학습되지 않은 alcohol-plus-food의 경우 삭제하는 것이 올바르다.
row수도 전체 비중에 비해 얼마되지 않아 삭제 진행!
최종적으로 train : 158583 // test : 17660
오늘 작업한 내용.
- 원핫인코딩 진행 후 pipeline 구현해 modeling으로 성능평가, grid search사용해 hyperparamter tuning 진행.
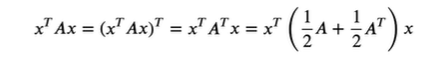




좋은 글 잘 읽었습니다, 감사합니다.