선형 회귀 모델

경사 하강법의 개요

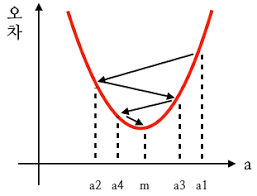
2차식의 그래프에서 x의 값에 a1, a2 그리고 m을 대입해 그 자리에서 미분하면 각 점에서의 순간 기울기가 그려집니다. 여기서 중요한 것은 m의 순간 기울기입니다. 그래프가 이차 함수의 포물선이므로 꼭짓점의 기울기는 x축과 평행한 선이 됩니다. 즉, 기울기가 0입니다.

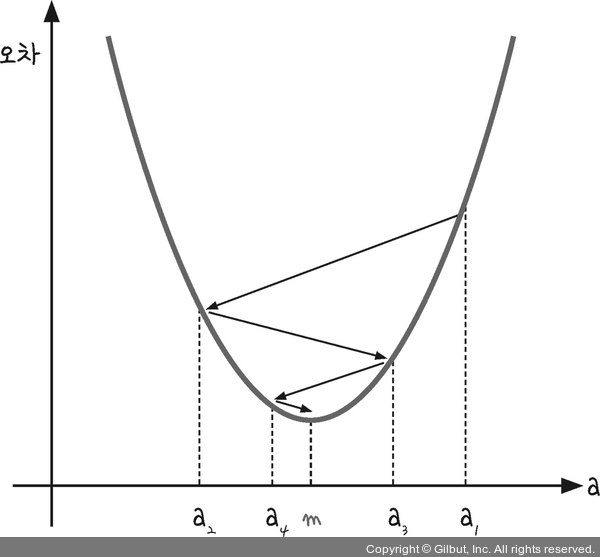
이를 찾기 위해서 다음 과정을 거칩니다.

1. a1에서 미분을 구한다
2. 구한 기울기의 반대 방향(기울기가 +면 음의 방향. -면 양의 방향)으로 얼마나 이동시킨 a2에서 미분을 구한다
3. 앞에서 구한 미분 값이 0이 아니면 1과 2 과정을 반복한다.

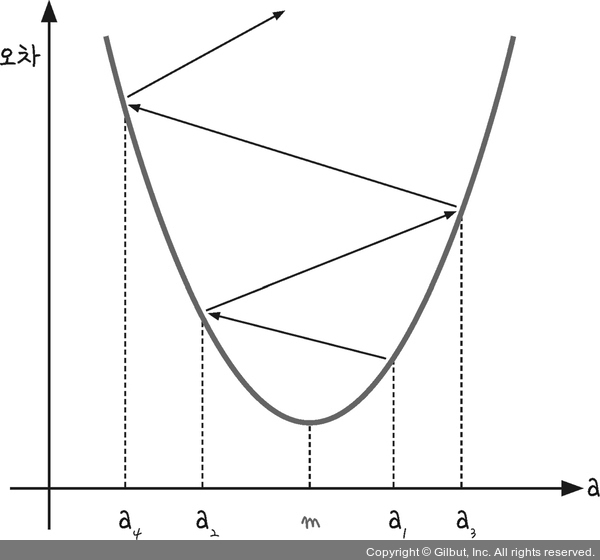
경사하강법은 이 과정을 반복해서 m의 값을 찾아내는 방법입니다.이때 기울기의 부호를 바꿔서 이동시킬 때 적절한 거리를 찾지 못하면 a값이 한 점으로 모이지 않고 그림과 같이 위로 치솟아 버립니다.

파이썬 코딩으로 확인하기

y_pred = a * x + b            # 예측 값을 구하는 식입니다.
error = y - y_pred            # 실제 값과 비교한 오차를 error로 놓습니다.

a_diff = (2/n) * sum(-x * (error))  # 오차 함수를 a로 편미분한 값입니다.
b_diff = (2/n) * sum(-(error))      # 오차 함수를 b로 편미분한 값입니다.
여기에 학습률을 곱해 기존의 a 값과 b 값을 업데이트합니다.

lr = 0.03               # 학습률을 정합니다.
a = a - lr * a_diff     # 학습률을 곱해 기존의 a 값을 업데이트합니다.
b = b - lr * b_diff     # 학습률을 곱해 기존의 b 값을 업데이트합니다.