[BaekJoon] 14476 최대공약수 하나 빼기 (Java)

1.  문제 링크

https://www.acmicpc.net/problem/14476

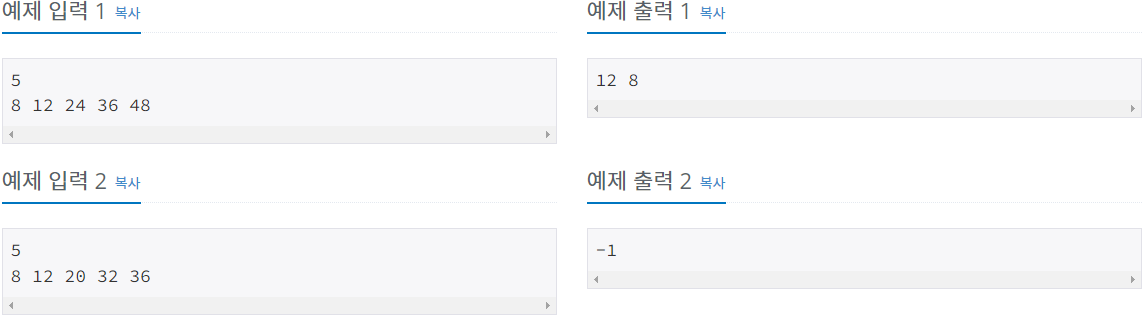
2.  문제

3.  소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
    static int N;
    static int[] nums;

    static void input() {
        Reader scanner = new Reader();

        N = scanner.nextInt();
        nums = new int[N + 2];

        for(int idx = 1; idx <= N; idx++)
            nums[idx] = scanner.nextInt();
    }

    static void solution() {
        int[] leftGcd = new int[N + 2], rightGcd = new int[N + 2];
        for(int idx = 1; idx <= N; idx++) leftGcd[idx] = gcd(nums[idx], leftGcd[idx - 1]);
        for(int idx = N; idx > 0; idx--) rightGcd[idx] = gcd(nums[idx], rightGcd[idx + 1]);

        int answer = Integer.MIN_VALUE, max = Integer.MIN_VALUE;
        for(int idx = 1; idx <= N; idx++) {
            int tempGcd = gcd(leftGcd[idx - 1], rightGcd[idx + 1]);
            if(tempGcd > max) {
                if(nums[idx] % tempGcd != 0) {
                    max = tempGcd;
                    answer = nums[idx];
                }
            }
        }

        if(answer == Integer.MIN_VALUE) System.out.println(-1);
        else System.out.println(max + " " + answer);
    }

    static int gcd(int num1, int num2) {
        if(num2 == 0) return num1;
        return gcd(num2, num1 % num2);
    }

    public static void main(String[] args) {
        input();
        solution();
    }

    static class Reader {
        BufferedReader br;
        StringTokenizer st;

        public Reader() {
            br = new BufferedReader(new InputStreamReader(System.in));
        }

        String next() {
            while(st == null || !st.hasMoreElements()) {
                try {
                    st = new StringTokenizer(br.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }

            return st.nextToken();
        }

        int nextInt() {
            return Integer.parseInt(next());
        }
    }
}

4.  접근

• 주어진 정수들의 순서대로 왼쪽부터의 최대공약수와 오른쪽부터의 최대공약수를 구합니다.
  • 예를 들어, 8, 12, 24, 36, 48이라는 수가 주어졌다면
    • 왼쪽부터 최대공약수를 구해나가면 8, 4, 4, 4, 4가 될 것이고
    • 오른쪽부터 최대공약수를 구해나가면 4, 12, 12, 12, 48가 될 것입니다.
• N개의 수에 대해서 첫 번째 수부터 하나씩 빼보면서 그 때의 최대공약수를 구하고 그 최대공약수가 뺀 수의 약수가 되지 않는 경우에 대해 최댓값을 갱신해나갑니다.
  • 최대공약수를 왼쪽, 오른쪽부터 각각 구해놨기 때문에 현재 빼고자 하는 수가 idx번째 수이고 왼쪽에서부터 구한 최대공약수들의 배열을 left, 오른쪽에서부터 구한 최대공약수들의 배열을 right라고 한다면, left[idx - 1]이 idx번째 수의 왼쪽에 있는 수들의 최대공약수가 될 것이고, right[idx + 1]이 idx번째 수의 오른쪽에 있는 수들의 최대공약수가 됩니다.
  • 그러므로 idx번째 수를 뺀 수들의 최대공약수는 left[idx - 1]과 right[idx + 1]의 최대공약수가 됩니다.
  • 문제의 조건에서 임의의 수 K를 뺐을 때, 나머지 N - 1개의 최대공약수가 K의 약수가 되면 안된다고 하였기 때문에 left[idx - 1]과 right[idx + 1]의 최대공약수, 즉 idx번째 수를 뺀 수들의 최대공약수가 idx번째 수의 약수가 되는지 확인하고 만약 그렇지 않다면 최대공약수의 최댓값을 갱신해나갑니다.