[BaekJoon] 17272 리그 오브 레전설 (Large) (Java)

1.  문제 링크

https://www.acmicpc.net/problem/17272

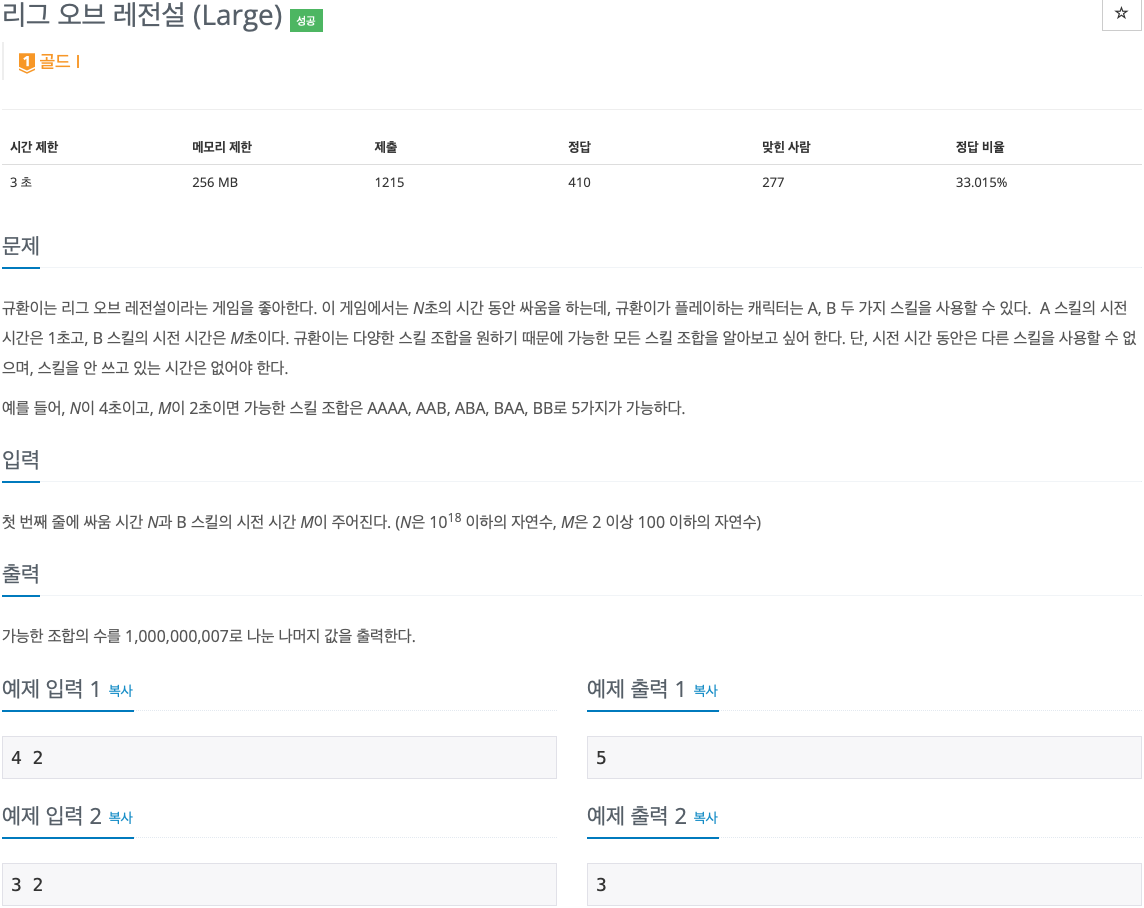
2.  문제

3.  소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    static final int DIVISOR = 1_000_000_007;

    static long fightTime;
    static int skillTime;

    static long[] dp;

    static void input() {
        Reader scanner = new Reader();

        fightTime = scanner.nextLong();
        skillTime = scanner.nextInt();
    }

    static void solution() {
        if(fightTime < skillTime) {
            System.out.println(1);
        } else if(fightTime == skillTime) {
            System.out.println(2);
        } else if(fightTime == skillTime + 1) {
            System.out.println(3);
        } else {
            int matSize = skillTime + 1;
            long powNum = fightTime - skillTime - 1;
            long[][] mat = new long[matSize][matSize];
            for(int row = 0; row < matSize - 1; row++) {
                mat[row][row + 1] = 1L;
            }
            mat[matSize - 1][1] = mat[matSize - 1][matSize - 1] = 1L;

            mat = power(powNum, mat);

            long answer = 0;
            for(int idx = 0; idx < matSize - 2; idx++) {
                answer = (answer + mat[matSize - 1][idx]) % DIVISOR;
            }
            answer = (answer + mat[matSize - 1][matSize - 2] * 2) % DIVISOR;
            answer = (answer + mat[matSize - 1][matSize - 1] * 3) % DIVISOR;

            System.out.println(answer);
        }
    }

    static long[][] power(long exponent, long[][] mat) {
        if(exponent == 1) {
            return mat;
        }

        long[][] temp = power(exponent / 2, mat);
        long[][] result = multiplyMatrix(temp, temp);
        if(exponent % 2 == 1) {
            result = multiplyMatrix(result, mat);
        }

        return result;
    }

    static long[][] multiplyMatrix(long[][] mat1, long[][] mat2) {
        long[][] result = new long[mat1.length][mat1[0].length];

        for(int row = 0; row < mat1.length; row++) {
            for(int col = 0; col < mat1[row].length; col++) {
                for(int idx = 0; idx < mat1[0].length; idx++) {
                    result[row][col] += ((mat1[row][idx] * mat2[idx][col]) % DIVISOR);
                    result[row][col] %= DIVISOR;
                }
            }
        }

        return result;
    }

    public static void main(String[] args) {
        input();
        solution();
    }

    static class Reader {
        BufferedReader br;
        StringTokenizer st;

        public Reader() {
            br = new BufferedReader(new InputStreamReader(System.in));
        }

        String next() {
            while (st == null || !st.hasMoreElements()) {
                try {
                    st = new StringTokenizer(br.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }

            return st.nextToken();
        }

        int nextInt() {
            return Integer.parseInt(next());
        }

        long nextLong() {
            return Long.parseLong(next());
        }
    }
}

4.  접근

N초 동안 스킬을 쓰는 것은 두 가지 경우가 존재한다.
1. N - 1초 동안 스킬을 쓰고 N초부터 스킬 A를 사용
2. N - M초 동안 스킬을 쓰고 N - M + 1초부터 스킬 B 사용

이를 통해 다음과 같이 점화식을 구할 수 있다.

$S_N = S_{N - 1} + S_{N - M}$

예시

• M = 3일 때,

  $S_N = S_{N - 1} + S_{N - 3}$

  이를 행렬로 표현하면 아래와 같이 표현할 수 있다.

  $\begin{pmatrix} S_{N - 3} \\ S_{N - 2} \\ S_{N - 1} \\ S_N\end{pmatrix} = \begin{pmatrix}0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1\end{pmatrix} \begin{pmatrix} S_{N - 4} \\ S_{N - 3} \\ S_{N - 2} \\ S_{N - 1}\end{pmatrix}$

• M = 4일 때,

  $S_N = S_{N - 1} + S_{N - 4}$

  이를 행렬로 표현하면 아래와 같이 표현할 수 있다.

  $\begin{pmatrix} S_{N - 4} \\ S_{N - 3} \\ S_{N - 2} \\ S_{N - 1} \\ S_N\end{pmatrix} = \begin{pmatrix}0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 1\end{pmatrix} \begin{pmatrix} S_{N - 5} \\ S_{N - 4} \\ S_{N - 3} \\ S_{N - 2} \\ S_{N - 1}\end{pmatrix}$

• 즉, $(M + 1) \times (M + 1)$ 행렬로 표현할 수 있다.

점화식

• 위와 같은 예시를 통해 점화식을 아래와 같이 표현할 수 있다.

  $\begin{pmatrix} S_{N - M} \\ S_{N - M + 1} \\ S_{N - M + 2} \\ ... \\ S_{N - 2} \\ S_{N - 1} \\ S_N\end{pmatrix} = \begin{pmatrix}0 & 1 & 0 & 0 & ... & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & ... & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & ... & 0 & 0 & 0 \\ & & & & ... \\ 0 & 0 & 0 & 0 & ... & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & ... & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & ... & 0 & 0 & 1\end{pmatrix} \begin{pmatrix} S_{N - 1 - M} \\ S_{N - 1 - M + 1} \\ S_{N - 1 - M + 2} \\ ... \\ S_{N - 3} \\ S_{N - 2} \\ S_{N - 1}\end{pmatrix}$

• 위와 같은 행렬을 거듭제곱하여 $\begin{pmatrix} S_1 \\ S_2 \\ S_3 \\ ... \\ S_M \\ S_{M + 1} \end{pmatrix}$꼴에 곱할 행렬을 구하면 최종 $S_N$을 구할 수 있다.
  
  
• $S_M$은 경우의 수가 2이고, $S_{M + 1}$은 경우의 수가 3이며, $S_1$부터 $S_{M - 1}$까지는 경우의 수가 1이다.
  • 즉, 거듭제곱한 행렬에서 마지막 두 자리에만 2, 3을 각각 곱해서 더해주고, 나머지는 그냥 더해주면 최종 정답을 구할 수 있다.