[BaekJoon] 2287 모노디지털 표현 (Java)

1.  문제 링크

https://www.acmicpc.net/problem/2287

2.  문제

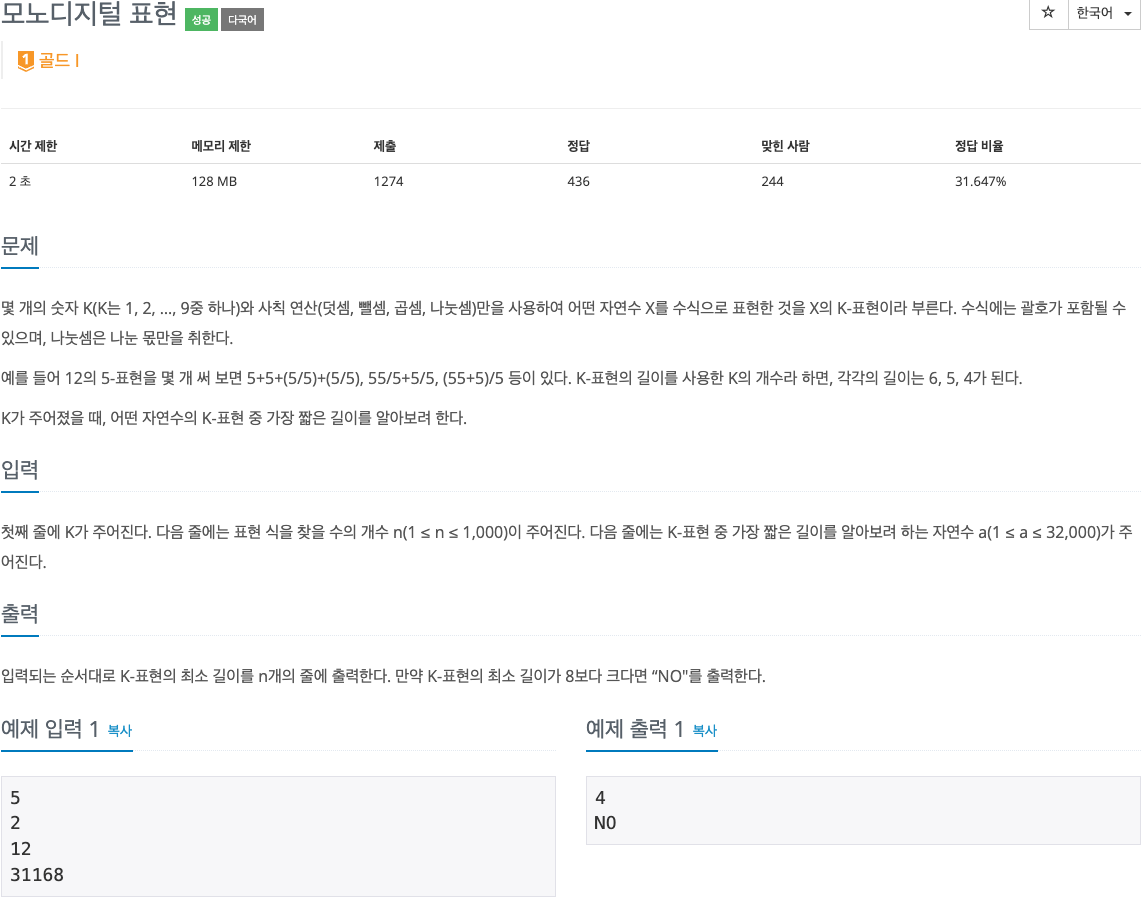
3.  소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.HashSet;
import java.util.Set;
import java.util.StringTokenizer;

public class Main {
    static final int MAX_LENGTH = 8; // K-표현의 최대 길이(8보다 크면 NO를 출력한다)

    // 각 K-표현 길이에서 나타낼 수 있는 숫자들을 나타내는 Set 배열
    static Set<Integer>[] possibleNumbers;
    static int k;
    static int testCnt;
    static int[] testCase;

    static void input() {
        Reader scanner = new Reader();

        k = scanner.nextInt();
        testCnt = scanner.nextInt();
        testCase = new int[testCnt];

        for (int idx = 0; idx < testCnt; idx++) {
            testCase[idx] = scanner.nextInt();
        }
    }

    /*
     * 최대 길이가 8이기 때문에 사전에 길이 8까지 각 길이에서 나타낼 수 있는 모든 숫자를 구한다
     *  - 각 길이에서 표현할 수 있는 수는 이전에 구한 더 작은 길이에서 표현할 수 있는 수를 이용할 수 있다
     *  - 예를 들어, 어떠한 길이에서 표현할 수 있는 수들을 E(X), 현재 길이를 L, 사칙연산을 통틀어 o라고 한다면
     *      - E(L) = E(1) o E(L - 1), E(2) o E(L - 2), ... , E(L - 2) o E(2), E(L - 1) o E(1)
     *  - 위와 같은 수식을 통해 현재 길이에서 표현할 수 있는 수들을 구할 수 있으니 이를 이용하여 모든 길이에서 나타낼 수 있는 모든 숫자를 구한다
     *
     * 모든 길이에서 나타낼 수 있는 숫자를 모두 구했으니 주어진 테스트케이스들에 대해서 가장 짧은 길이인 1부터 시작하여 모든 길이들을 순회하며
     * 해당 테스트케이스가 나오는 가장 짧은 길이를 구하면 그 길이가 K-표현 중 가장 짧은 길이가 된다
     */
    static void solution() {
        findAllPossibleNumbers();

        StringBuilder sb = new StringBuilder();

        for (int idx = 0; idx < testCnt; idx++) {
            sb.append(findMinLength(testCase[idx])).append('\n');
        }
        System.out.print(sb);
    }

    static String findMinLength(int targetNumber) {
        for (int len = 1; len <= MAX_LENGTH; len++) {
            if (possibleNumbers[len].contains(targetNumber)) {
                return String.valueOf(len);
            }
        }

        return "NO";
    }

    static void findAllPossibleNumbers() {
        init();

        // 길이가 1일 때는 자기 자신만 표현할 수 있고, 이를 init 메서드에서 설정하였으니
        // 길이가 2일 때부터 8일 때까지 순회하며 각 길이에서 나타낼 수 있는 숫자를 구한다
        for (int len = 2; len <= MAX_LENGTH; len++) {
            // 위에서 말한 수식을 이용하여 나타낼 수 있는 숫자를 구할 것인데
            // 절반을 기준으로 앞뒤 순서만 바뀐 것이므로 절반까지만 순회하며 앞뒤 순서를 바꿔가며 나타낼 수 있는 숫자들을 찾는다
            for (int basis = 1; basis <= len / 2; basis++) {
                calculatePossibleNumbersBetweenTwoSize(len, basis, len - basis);
                calculatePossibleNumbersBetweenTwoSize(len, len - basis, basis);
            }

            // 위에서 구한 수 뿐만 아니라 자기 자신을 len번만큼 반복한 수 역시 나타낼 수 있기 때문에 이 수 또한 포함시킨다
            String kStr = String.valueOf(k);
            kStr = kStr.repeat(len);
            possibleNumbers[len].add(Integer.parseInt(kStr));
        }
    }

    static void init() {
        possibleNumbers = new HashSet[MAX_LENGTH + 1];
        for (int idx = 0; idx <= MAX_LENGTH; idx++) {
            possibleNumbers[idx] = new HashSet<>();
        }

        // 길이가 1인 경우에는 표현할 수 있는 수가 자기 자신밖에 없으므로 자기 자신만 넣는다
        possibleNumbers[1].add(k);
    }

    static void calculatePossibleNumbersBetweenTwoSize(int length, int firstLength, int secondLength) {
        for (int firstLenPossibleNumber : possibleNumbers[firstLength]) {
            for (int secondLenPossibleNumber : possibleNumbers[secondLength]) {
                possibleNumbers[length].add(firstLenPossibleNumber + secondLenPossibleNumber);
                possibleNumbers[length].add(firstLenPossibleNumber - secondLenPossibleNumber);
                possibleNumbers[length].add(firstLenPossibleNumber * secondLenPossibleNumber);
                try {
                    possibleNumbers[length].add(firstLenPossibleNumber / secondLenPossibleNumber);
                } catch (Exception e) {
                }
            }
        }
    }

    public static void main(String[] args) {
        input();
        solution();
    }

    static class Reader {
        BufferedReader br;
        StringTokenizer st;

        public Reader() {
            br = new BufferedReader(new InputStreamReader(System.in));
        }

        String next() {
            while (st == null || !st.hasMoreElements()) {
                try {
                    st = new StringTokenizer(br.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }

            return st.nextToken();
        }

        int nextInt() {
            return Integer.parseInt(next());
        }
    }
}