[BaekJoon] 2533 사회망 서비스(SNS) (Java)

1.  문제 링크

https://www.acmicpc.net/problem/2533

2.  문제

요약

• 사회망에서 사람들의 친구 관계는 그래프로 표현할 수 있는데, 사람은 정점으로 표현되고, 두 정점을 잇는 에지는 두 정점으로 표현되는 두 사람이 서로 친구 관계임을 표현합니다.
• 어떤 새로운 아이디어를 먼저 받아들인 사람을 얼리아답터라고 하는데, 사회망 서비스에 속한 사람들은 얼리아답터이거나 얼리아답터가 아닙니다.
• 얼리아답터가 아닌 사람들은 자신의 모든 친구들이 얼리아답터일 때만 이 아이디어를 받아들입니다.
• 어떤 아이디어를 사회망 서비스에 퍼뜨리고자 할 때, 가능한 한 최소의 수의 얼리아답터를 확보하여 모든 사람이 이 아이디어를 받아들이게 하려고 합니다.
• 친구 관계 그래프는 트리인 경우, 즉 모든 두 정점 사이에 이들을 잇는 경로가 존재하면서 사이클이 존재하지 않는 경우만 고려합니다.
• 친구 관계 트리가 주어졌을 때, 모든 개인이 새로운 아이디어를 수용하기 위하여 필요한 최소 얼리아답터의 수를 구하는 문제입니다.
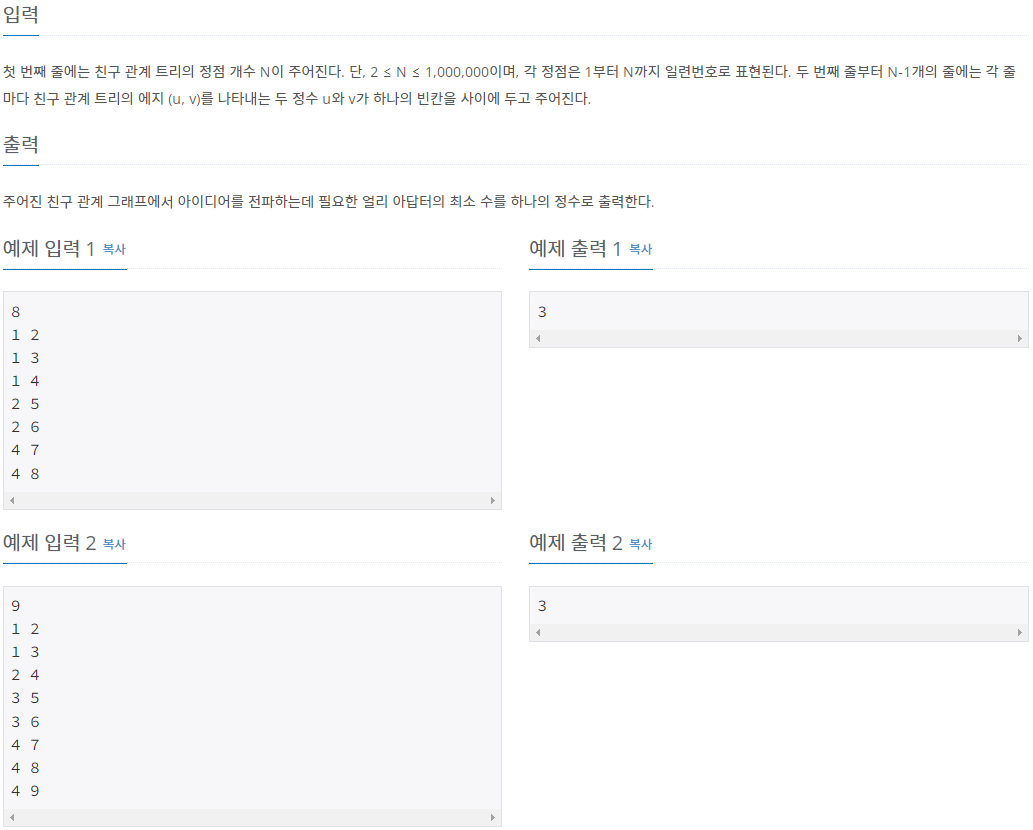
• 입력: 첫 번째 줄에 2보다 크거나 같고 1,000,000보다 작거나 같은 친구 관계 트리의 정점 개수 N이 주어지고 두 번째 줄부터 N - 1개의 줄에 친구 관계 트리의 에지 (u, v)를 나타내는 두 정수 u와 v가 주어집니다.
  • 각 정점은 1부터 N까지 일련번호로 표현됩니다.
• 출력: 첫 번째 줄에 주어진 친구 관계 그래프에서 아이디어를 전파하는데 필요한 얼리아답터의 최소 수를 하나의 정수로 출력합니다.

3.  소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class Main {
    static int N;
    static HashMap<Integer, LinkedList<Integer>> tree;
    static boolean[] visited;
    static int[][] dp;
    static void input() {
        Reader scanner = new Reader();
        N = scanner.nextInt();
        tree = new HashMap<>();
        for(int node = 1; node <= N; node++) tree.put(node, new LinkedList<>());
        for(int edge = 0; edge < N - 1; edge++) {
            int node1 = scanner.nextInt(), node2 = scanner.nextInt();
            tree.get(node1).add(node2);
            tree.get(node2).add(node1);
        }
    }

    static void solution() {
        visited = new boolean[N + 1];
        dp = new int[N + 1][2];
        findEarlyAdaptor(1);
        System.out.println(Math.min(dp[1][0], dp[1][1]));
    }

    static void findEarlyAdaptor(int node) {
        visited[node] = true;
        dp[node][0] = 0;
        dp[node][1] = 1;

        for(int n : tree.get(node)) {
            if(!visited[n]) {
                findEarlyAdaptor(n);
                dp[node][0] += dp[n][1];
                dp[node][1] += Math.min(dp[n][0], dp[n][1]);
            }
        }
    }

    public static void main(String[] args) {
        input();
        solution();
    }

    static class Reader {
        BufferedReader br;
        StringTokenizer st;
        public Reader() {
            br = new BufferedReader(new InputStreamReader(System.in));
        }
        String next() {
            while(st == null || !st.hasMoreElements()) {
                try {
                    st = new StringTokenizer(br.readLine());
                } catch(IOException e) {
                    e.printStackTrace();
                }
            }
            return st.nextToken();
        }
        int nextInt() {
            return Integer.parseInt(next());
        }
    }
}

4.  접근

• 주어진 에지 정보를 이용하여 트리를 생성합니다.
• DFS를 이용하여 각 사람들이 얼리아답터일 때와 아닐 때를 설정하여 그에 맞게 얼리아답터의 수를 결정합니다.

  • 만약 현재 탐색하고 있는 사람이 얼리아답터가 아니라면 그 사람과 이웃한 사람들은 모두 얼리아답터여야만 합니다.

  • 만약 현재 탐색하고 있는 사람이 얼리아답터라면 이웃한 사람들은 얼리아답터일 수도 있고 그렇지 않을 수도 있습니다.

  • 그렇기 때문에 우선 현재 탐색하고 있는 사람을 방문했다는 의미로 그 사람의 visited 값을 true로 변경합니다.

  • 2차원 배열 dp를 이용하는데 이는 다음을 의미합니다.

    • dp[node][0] : node에 해당하는 사람이 얼리아답터가 아닐 때 얼리아답터의 수
    • dp[node][1] : node에 해당하는 사람이 얼리아답터일 때 얼리아답터의 수

  • 우선 현재 탐색하고 있는 사람의 dp 배열의 초기값은 본인이 얼리어답터가 아니라면 0로, 본인이 얼리어답터라면 한 명이 존재하기 때문에 1로 합니다.

  • 현재 탐색하고 있는 사람의 이웃한 사람들을 모두 확인하여 만약 그 사람이 아직 방문되지 않았다면 재귀를 통해 그 사람에 대해서도 탐색합니다.

  • 모든 이웃한 사람을 탐색한 이후에 현재 탐색하고 있는 사람의 dp 배열의 값은 아래와 같습니다.

    • dp[node][0] = dp[node][0] + dp[n][1] -> 현재 탐색하고 있는 사람이 얼리아답터가 아니기 때문에 이웃한 사람들은 모두 얼리아답터여야하므로 이웃한 사람 n의 dp[n][1]의 값을 가져와 더해줍니다.
    • dp[node][1] = dp[node][1] + min(dp[n][0], dp[n][1]) -> 현재 탐색하고 있는 사람이 얼리아답터이기 때문에 이웃한 사람들은 얼리아답터여도 되고 아니어도 됩니다. 그렇기 때문에 우리는 얼리아답터의 최솟값을 구하는 것이므로 이웃한 사람이 얼리아답터가 아닌 경우인 dp[n][0]과 이웃한 사람이 얼리아답터인 경우인 dp[n][1] 중에서 더 작은 값을 가져와 더해줍니다.
• 모든 사람을 방문하여 DFS가 끝난 후에 dp[1][0]과 dp[1][1] 중 더 작은 값을 출력합니다.