1. 문제 링크
https://www.acmicpc.net/problem/3037
2. 문제

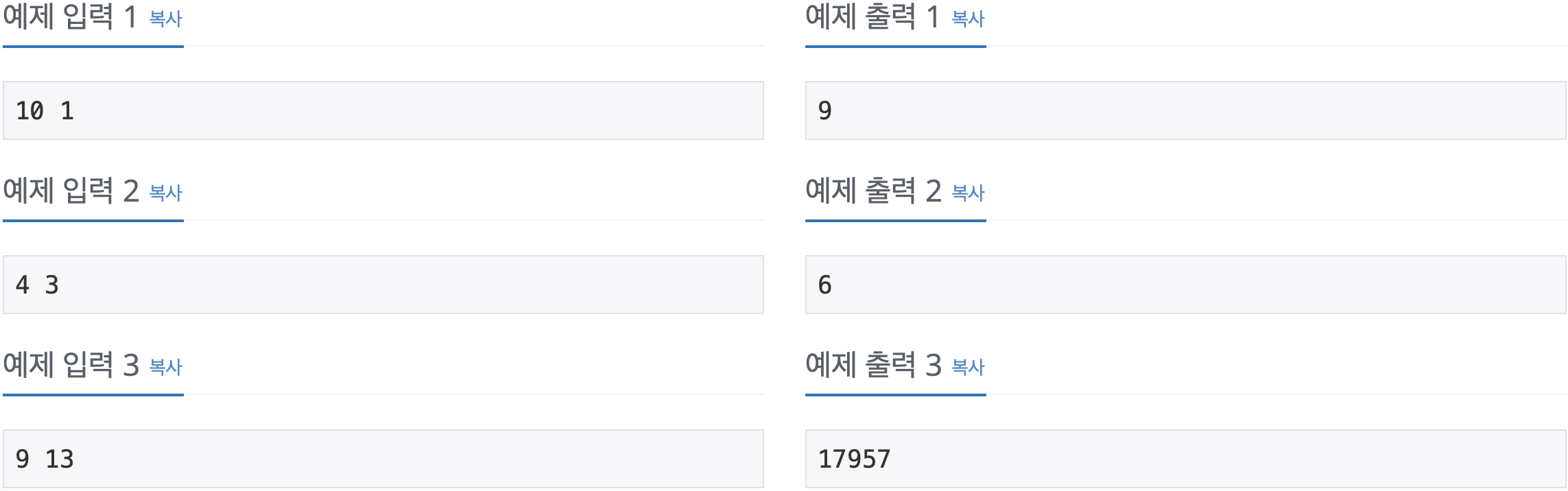
3. 소스코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
static final int DIVISOR = 1_000_000_007;
static int seriesCount;
static int confusion;
static void input() {
Reader scanner = new Reader();
seriesCount = scanner.nextInt();
confusion = scanner.nextInt();
}
/*
* dp[series][confusion]
* - series개의 자연수로 이루어진 수열에 대해 혼란도가 0부터 confusion까지 수열의 개수의 누적합
*
* 4개의 자연수로 이루어진 수열에 대해 혼란도가 4인 수열의 개수를 구해보자
* arr 2차원 배열이 series개의 자연수로 이루어진 수열에 대해 혼란도가 confusion인 수열의 개수를 담고 있는 배열이라고 하자
* 1) 1개의 자연수로 이루어진 수열
* - 쌍을 이룰 수 있는 두 수가 없기 때문에 모든 혼란도에서 수열의 개수가 0이 된다
* 2) 2개의 자연수로 이루어진 수열
* - 혼란도가 0일 때에는 [1, 2] 1개가 존재
* - 혼란도가 1일 때에는 [2, 1] 1개가 존재
* - 혼란도가 2 ~ 4일 때에는 해당하는 수열이 없음
* 3) 3개의 자연수로 이루어진 수열
* - 혼란도가 0일 때
* - [1, 2, 3] 1개가 존재
* - 혼란도가 1일 때
* - 1부터 시작할 때에는 [1, 3, 2]
* - 하나의 자리수가 정해져있으니 이를 제외하고 2개의 수를 이용해 혼란도가 1인 경우를 구하는 것과 같다
* - 그러므로 arr[2][1]
* - 2부터 시작할 때에는 [2, 3, 1]
* - 하나의 자리수가 정해져있고 혼란도가 이미 1이 채워지게 된다 (2가 1보다 큰데 1보다 앞에 있으니)
* - 그러므로 2개의 수를 이용해 혼란도가 0인 경우를 구하는 것과 같다 -> arr[2][0]
* - 3부터 시작할 때에는 이미 3보다 작은 1, 2보다 3이 앞에 있으니 혼란도 2가 채워지게 되어 혼란도가 1인 경우는 없다
* - 혼란도가 2일 때
* - 1부터 시작할 때
* - 하나의 자리수가 정해져있으니 이를 제외하고 2개의 수를 이용해 혼란도가 2인 경우를 구하는 것과 같다
* - 그러므로 arr[2][2]
* - 2부터 시작할 때
* - 하나의 자리수가 정해져있고 혼란도가 이미 1이 채워지므로 2개의 수를 이용해 혼란도가 1인 경우를 구하는 것과 같다
* - 그러므로 arr[2][1]
* - 3부터 시작할 때
* - 하나의 자리수가 정해져있고 혼란도가 이미 2가 채워지므로 2개의 수를 이용해 혼란도가 0인 경우를 구하는 것과 같다
* - 그러므로 arr[2][0]
* - 혼란도가 3일 때
* - 1부터 시작할 때
* - 하나의 자리수가 정해져있으니 이를 제외하고 2개의 수를 이용해 혼란도가 3인 경우를 구하는 것과 같다
* - 그러므로 arr[2][3]
* - 2부터 시작할 때
* - 하나의 자리수가 정해져있고 혼란도가 이미 1이 채워지므로 2개의 수를 이용해 혼란도가 2인 경우를 구하는 것과 같다
* - 그러므로 arr[2][2]
* - 3부터 시작할 때
* - 하나의 자리수가 정해져있고 혼란도가 이미 2가 채워지므로 2개의 수를 이용해 혼란도가 1인 경우를 구하는 것과 같다
* - 그러므로 arr[2][1]
* - 혼란도가 4일 때
* - 1부터 시작할 때
* - 하나의 자리수가 정해져있으니 이를 제외하고 2개의 수를 이용해 혼란도가 4인 경우를 구하는 것과 같다
* - 그러므로 arr[2][4]
* - 2부터 시작할 때
* - 하나의 자리수가 정해져있고 혼란도가 이미 1이 채워지므로 2개의 수를 이용해 혼란도가 3인 경우를 구하는 것과 같다
* - 그러므로 arr[2][3]
* - 3부터 시작할 때
* - 하나의 자리수가 정해져있고 혼란도가 이미 2가 채워지므로 2개의 수를 이용해 혼란도가 2인 경우를 구하는 것과 같다
* - 그러므로 arr[2][2]
* 4) 4개의 자연수로 이루어진 수열
* - 혼란도가 0일 때
* - [1, 2, 3, 4] 1개가 존재
* - 혼란도가 1일 때
* - 1부터 시작할 때
* - 하나의 자리수가 정해져있으니 이를 제외하고 3개의 수를 이용해 혼란도가 1인 경우를 구하는 것과 같다
* - 그러므로 arr[3][1]
* - 2부터 시작할 때
* - 하나의 자리수가 정해져있고 혼란도가 이미 1이 채워지므로 3개의 수를 이용해 혼란도가 0인 경우를 구하는 것과 같다
* - 그러므로 arr[3][0]
* - 혼란도가 2일 때
* - 1부터 시작할 때
* - 하나의 자리수가 정해져있으니 이를 제외하고 3개의 수를 이용해 혼란도가 2인 경우를 구하는 것과 같다
* - 그러므로 arr[3][2]
* - 2부터 시작할 때
* - 하나의 자리수가 정해져있고 혼란도가 이미 1이 채워지므로 3개의 수를 이용해 혼란도가 1인 경우를 구하는 것과 같다
* - 그러므로 arr[3][1]
* - 3부터 시작할 때
* - 하나의 자리수가 정해져있고 혼란도가 이미 2가 채워지므로 3개의 수를 이용해 혼란도가 0인 경우를 구하는 것과 같다
* - 그러므로 arr[3][0]
* - 혼란도가 3일 때
* - 1부터 시작할 때
* - 하나의 자리수가 정해져있으니 이를 제외하고 3개의 수를 이용해 혼란도가 3인 경우를 구하는 것과 같다
* - 그러므로 arr[3][3]
* - 2부터 시작할 때
* - 하나의 자리수가 정해져있고 혼란도가 이미 1이 채워지므로 3개의 수를 이용해 혼란도가 2인 경우를 구하는 것과 같다
* - 그러므로 arr[3][2]
* - 3부터 시작할 때
* - 하나의 자리수가 정해져있고 혼란도가 이미 2가 채워지므로 3개의 수를 이용해 혼란도가 1인 경우를 구하는 것과 같다
* - 그러므로 arr[3][1]
* - 4부터 시작할 때
* - 하나의 자리수가 정해져있고 혼란도가 이미 3이 채워지므로 3개의 수를 이용해 혼란도가 0인 경우를 구하는 것과 같다
* - 그러므로 arr[3][0]
* - 혼란도가 4일 때
* - 1부터 시작할 때
* - 하나의 자리수가 정해져있으니 이를 제외하고 3개의 수를 이용해 혼란도가 4인 경우를 구하는 것과 같다
* - 그러므로 arr[3][4]
* - 2부터 시작할 때
* - 하나의 자리수가 정해져있고 혼란도가 이미 1이 채워지므로 3개의 수를 이용해 혼란도가 3인 경우를 구하는 것과 같다
* - 그러므로 arr[3][3]
* - 3부터 시작할 때
* - 하나의 자리수가 정해져있고 혼란도가 이미 2가 채워지므로 3개의 수를 이용해 혼란도가 2인 경우를 구하는 것과 같다
* - 그러므로 arr[3][2]
* - 4부터 시작할 때
* - 하나의 자리수가 정해져있고 혼란도가 이미 3이 채워지므로 3개의 수를 이용해 혼란도가 1인 경우를 구하는 것과 같다
* - 그러므로 arr[3][1]
*
* 위 예시를 통해 점화식을 구할 수 있다
* - arr[series][confusion] = arr[series - 1][confusion] + arr[series - 1][confusion - 1] + arr[series - 1][confusion - 2] + ... + arr[series - 1][confusion - (series - 1)]
* - 만약 confusion - (series - 1)이 0보다 작거나 같다면 arr[series - 1][0]부터 arr[series - 1][confusion]까지의 합을 의미
* 그러나 매 게산마다 위와 같이 confusion - (series - 1)부터 confusion까지 더해나간다면 시간이 오래 걸린다
* 그러므로 애초에 dp 배열에 누적합을 구해놓고 최종 답을 구할 때 dp[series][confusion] - dp[series][confusion - 1]을 구한다
* modulo 연산의 분배 법칙에서 뺄셈에 대한 분배법칙은 아래와 같다
* - (a - b) % p = ((a % p) - (b % p) + p) % p
* - 뺄셈을 했을 때 음수가 나오는 것을 막기 위해 p를 더한 후 p로 modulo 연산을 취한다
* 이를 이용하여 최종 답을 구한다
*/
static void solution() {
if (seriesCount == 1) {
System.out.println(0);
return;
}
if (confusion == 0) {
System.out.println(1);
return;
}
int[][] dp = new int[seriesCount + 1][confusion + 1];
init(dp);
fillAllNumberOfSeries(dp);
System.out.println((dp[seriesCount][confusion] - dp[seriesCount][confusion - 1] + DIVISOR) % DIVISOR);
}
static void init(int[][] dp) {
dp[2][0] = 1;
for (int idx = 1; idx <= confusion; idx++) {
dp[2][idx] = 2;
}
}
static void fillAllNumberOfSeries(int[][] dp) {
for (int series = 3; series <= seriesCount; series++) {
dp[series][0] = 1;
fillNumberOfSeriesByConfusion(series, dp);
}
}
static void fillNumberOfSeriesByConfusion(int series, int[][] dp) {
for (int c = 1; c <= confusion; c++) {
int firstElementConfusion = c - (series - 1);
calculateNumberOfSeries(series, firstElementConfusion, c, dp);
}
}
static void calculateNumberOfSeries(int series, int firstElementConfusion, int confusion, int[][] dp) {
if (firstElementConfusion <= 0) {
dp[series][confusion] = (dp[series][confusion - 1] + dp[series - 1][confusion]) % DIVISOR;
return;
}
dp[series][confusion] = (dp[series][confusion - 1]
+ (dp[series - 1][confusion] - dp[series - 1][firstElementConfusion - 1]) % DIVISOR) % DIVISOR;
}
public static void main(String[] args) {
input();
solution();
}
static class Reader {
BufferedReader br;
StringTokenizer st;
public Reader() {
br = new BufferedReader(new InputStreamReader(System.in));
}
String next() {
while (st == null || !st.hasMoreElements()) {
try {
st = new StringTokenizer(br.readLine());
} catch (IOException e) {
e.printStackTrace();
}
}
return st.nextToken();
}
int nextInt() {
return Integer.parseInt(next());
}
}
}
