Multi-factor design experiment의 데이터가 정규성을 만족하지 못할 때, 우리는 데이터에 Aligned Rank Transform을 수행한 다음 parametric test (i.e., Factorial ANOVA)를 수행할 수 있다. Aligned Rank Transform은 (1) Data Alignment, (2) Rank Transform 순서로 Data Transform이 이뤄지는 과정이며 Wobbrock et al.의 논문[3]에 각 세부 과정이 설명되어 있다.
Rank Transform & Data Alignment
Conover and Iman [2]-(1981)이 rank transformed data에 parametric F-test를 수행하는 방법을 제안했고, 이후 연구들 [4]에서 이 방식이 부정확한 interaction effect를 도출함을 확인했다고 한다. 그 후 Aligned Rank Transform [5]이 rank transform 이전에 data alignment [6] 과정을 거치는 방식으로 이러한 문제를 보완했다고 한다. F-test on rank가 valid한 이유, Data alignment process가 기존의 문제를 보완하는 이유 등은 관련 논문들 [2,3,4,5,6]에 설명이 되어있다. 사실 제대로 이해해보려고 뛰어들었다가 먼저 알아야 하는 선행 통계 지식들이 너무 많이 엮여 있어서 포기하고 그냥 사용하기로 했다.
ARTool R Package by Wobbrock et al.
ARTool는 Wobbrock et al.이 배포한 ART 툴이다. 윈도우 버전 Executable 프로그램은 데이터를 규격에 맞춰 .csv 파일로 준비하면 각 factor 및 factor의 조합 별로 Data Alignment & Rank Transform을 데이터에 수행한 값들을 뽑아준다. 하지만 각 main effect 및 interaction effect를 확인하기 위한 여러 번의 ANOVA는 직접 다른 소프트웨어에서 수행해야 한다. 직접 해봤는데 매우 귀찮다. R 패키지를 쓰는게 좋다. R 패키지는 데이터만 dataframe 으로 만들어서 art() 함수에 넣어주면 모든 effect를 한 번에 뽑아준다.
R Codes
(1) ARTool 패키지 설치 및 로드
install.packages ("ARTool")
library(ARTool)(2) data frame 준비 아래와 같은 규격이 되어야 한다. 1번째 column은 subject (실제 계산에 사용되지는 않는다), 가장 오른쪽 column은 response, 그 사이는 independent variable이 factor 자료형으로 준비되어야 한다. dplyr 패키지의 group_by() 메소드를 사용하면 아래 규격을 만들기 쉽다.
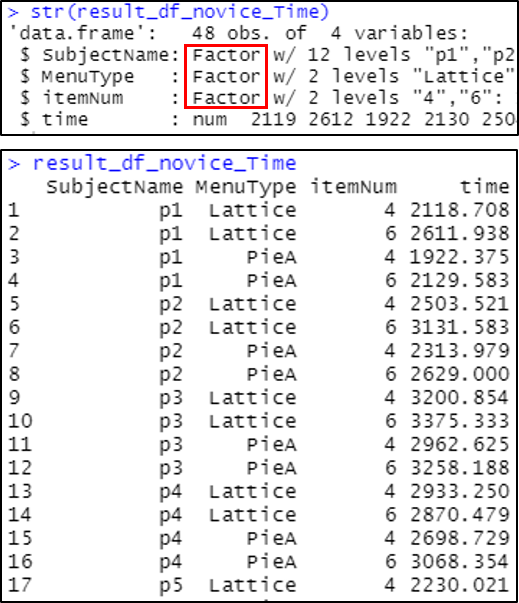
data.frame contents for ART process
(3) ART 및 ANOVA 메소드 수행 Repeated measures의 경우 아래와 같이 Error(SubjectName/(MenuType*itemNum)), Repeated measures가 아닌 경우는 (1|SubjectName)으로 입력하면 된다 [8].
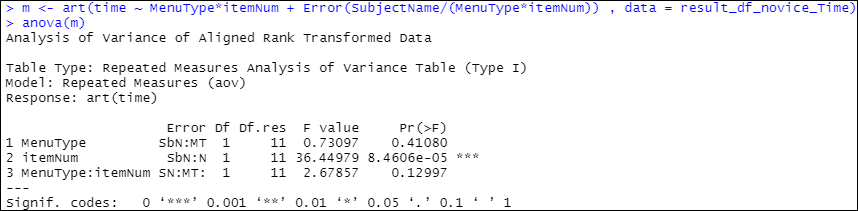
Results of ART & ANOVA
통계 분석 결과
MenuType has no statistically significant effect on time but itemNum has statistically significant effect on time (p < .001).
MenuType은 time에 통계적으로 유의미한 영향을 미치지 않지만, itemNum은 통계적으로 유의미한 영향을 미친다 (p < .001)
참고
[1] https://en.wikipedia.org/wiki/ANOVA_on_ranks
[2] Conover, William J., and Ronald L. Iman. "Rank transformations as a bridge between parametric and nonparametric statistics." The American Statistician 35.3 (1981): 124-129.
[3] Wobbrock, Jacob O., et al. "The aligned rank transform for nonparametric factorial analyses using only anova procedures." Proceedings of the SIGCHI conference on human factors in computing systems. 2011.
[4] Salter, K. C., and R. F. Fawcett. "The ART test of interaction: a robust and powerful rank test of interaction in factorial models." Communications in Statistics-Simulation and Computation 22.1 (1993): 137-153.
[5] Wobbrock, Jacob O., et al. "The aligned rank transform for nonparametric factorial analyses using only anova procedures." Proceedings of the SIGCHI conference on human factors in computing systems. 2011.
[6] Hodges, J. L., and Erich L. Lehmann. "Rank methods for combination of independent experiments in analysis of variance." Selected Works of EL Lehmann. Springer, Boston, MA, 2012. 403-418.
[7] http://depts.washington.edu/acelab/proj/art/index.html
[8] https://cran.r-project.org/web/packages/ARTool/ARTool.pdf
변경 이력
- 2021년 9월 3일: 글 등록
- 2021년 9월 24일: 글 보완
- 2021년 12월 1일: Velog로 이전
