Geometry - Matrix Equation

Matrix x Vector

---

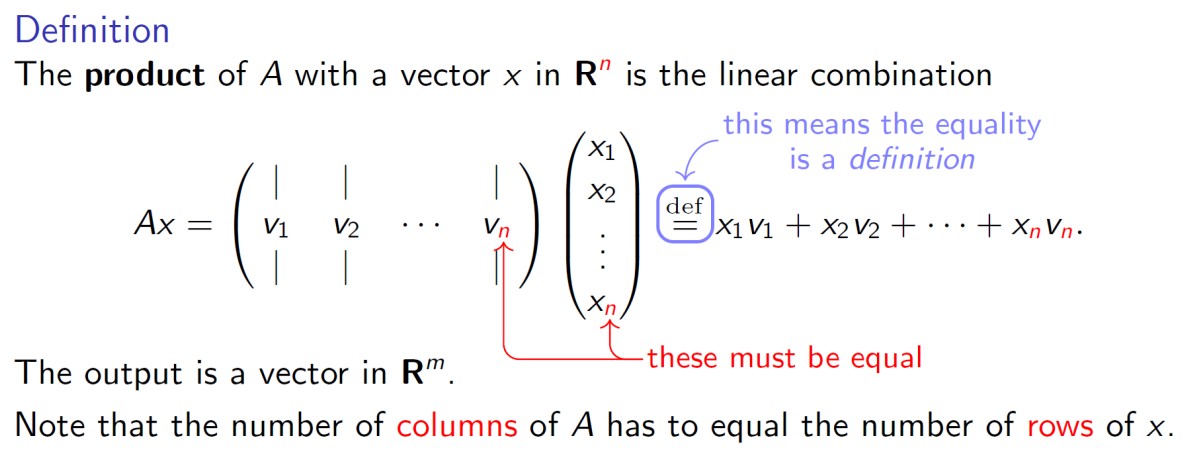
반드시 Matrix의 열의 수와 Vector의 행의 수가 일치해야 곱할 수 있음

Matrix Equation

---

$x_{1}v_{1} + x_{2}v_{2} + ... + x_{p}v_{p} = b$ 해당 식을 $Ax = b$와 같이 표현할 수 있고 이를 Matrix Equation이라고 한다.

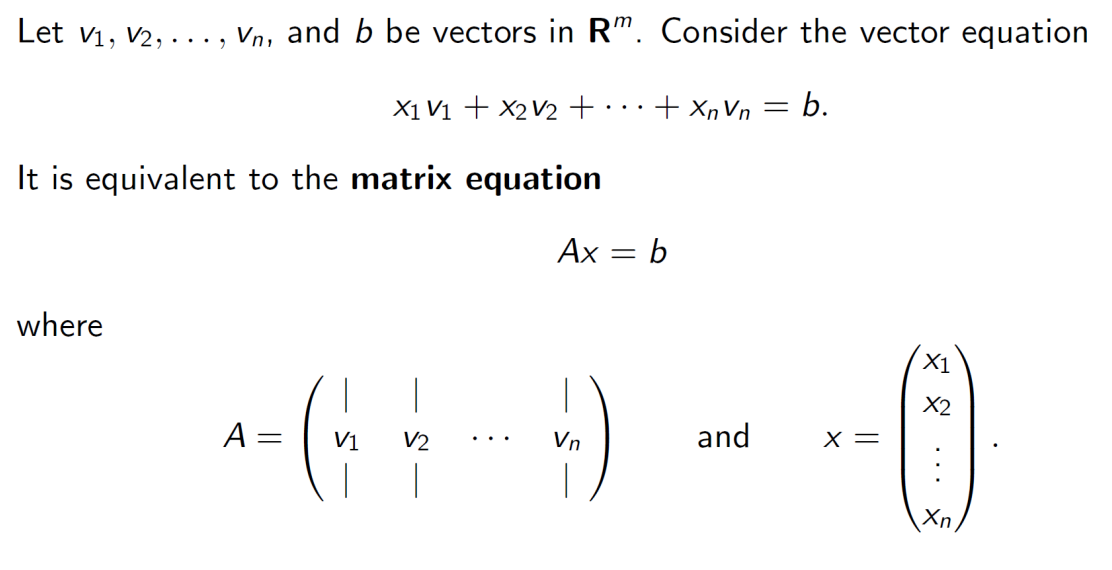
지금까지 배운것을 정리해보면 우리는 아래와 같이 동일한 식을 표현할 수 있고, 이때의 해는 모두 동일하다.

1. System of Equation
2. Augmented Equation
3. Vector Equation
4. Matrix Equation

행백터로의 표현

---

동일한 식을 다음과 같이 두가지 관점에서 바라볼 수 있다.

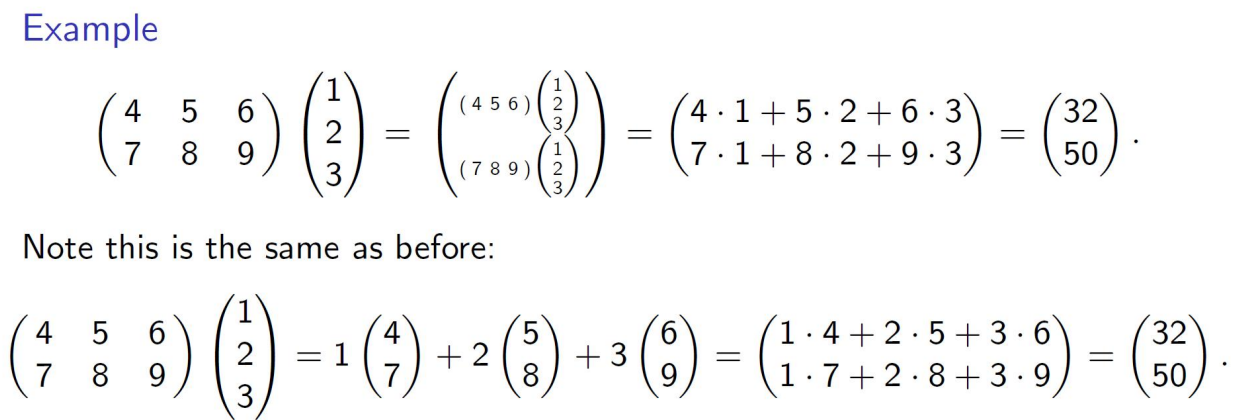
Spans and Solution of Equations

---

$Ax = b$가 해를 가지고 있다 >> b는 A를 구성하는 columns에 의해 Span된다.

예시 링크

When Solutions Always Exist

---

Non-Augmented $m$ x $n$ Matrix $A$에 대하여 아래의 조건을 만족하면 항상 해가 존재한다.

1. $Ax = b$가 $R^m$에 존재하는 모든 b에 대해 해가 존재할 때
2. $A$의 Span이 $R^m$인 경우
3. 모든 행에 pivot이 존재하는 경우

3번식의 경우, A를 Augmented 시키더라도 마지막 행이 Pivot column이 될 수 없기 때문에 만족한다.

Properties of the Matrix - Vector Product

---

선형성에 의거하여, $Ax=0$를 만족하는 벡터 {$u$,$v$}를 구한경우 $Ax = 0$의 solution set은 반드시 Span이다.