kNN

불러왔던 cifar10 데이터셋을 사용하여 구현한다.
from cs231n.classifiers import KNearestNeighbor
# Create a kNN classifier instance.
# Remember that training a kNN classifier is a noop:
# the Classifier simply remembers the data and does no further processing
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
# compute_distance_two_loops 구현하기
각 이미지의 거리 차 구하기
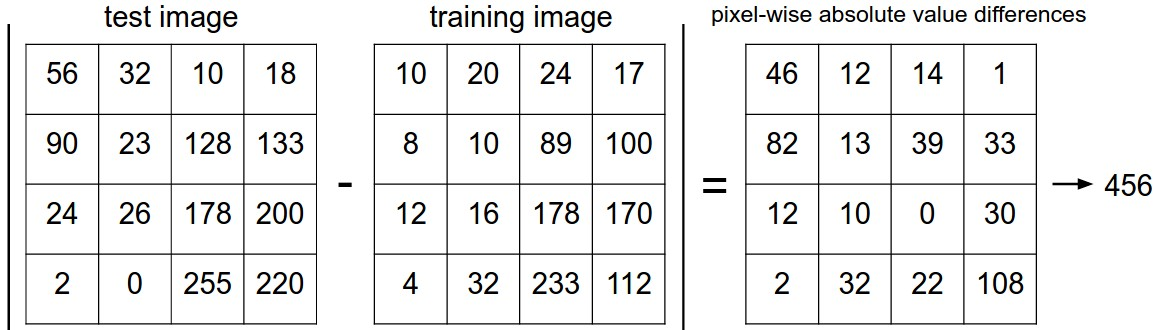
kNearestNeighbor class의 twoloop 함수 구현
def compute_distances_two_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a nested loop over both the training data and the
test data.
Inputs:
- X: A numpy array of shape (num_test, D) containing test data.
Returns:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
is the Euclidean distance between the ith test point and the jth training
point.
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train)) # 0으로 체워진 array 생성
for i in range(num_test):
for j in range(num_train):
#####################################################################
# TODO: #
# Compute the l2 distance between the ith test point and the jth #
# training point, and store the result in dists[i, j]. You should #
# not use a loop over dimension, nor use np.linalg.norm(). #
#####################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# 유클리드 거리 구하는 법
# np.square() : 제곱
# np.sum() : 합
# np.sqrt() : 제곱근
dists[i, j] = np.sqrt(np.sum(np.square(X[i] - self.X_train[j])))
# dists[i, j] = np.linalg.norm(X[i] - self.X_train[j]) # 위의 식과 같은 결과
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return dists코드 실행
# Open cs231n/classifiers/k_nearest_neighbor.py and implement
# compute_distances_two_loops.
# Test your implementation:
dists = classifier.compute_distances_two_loops(X_test)
print(dists.shape)(500, 5000)
데이터 이미지 metrix 확인
# We can visualize the distance matrix: each row is a single test example and
# its distances to training examples
plt.imshow(dists, interpolation='none')
plt.show()
# 검정색은 짧은거리, 흰색은 긴 거리를 나타냄
# 흰색뒤에 검정색이 오는 이유는 다른 종류의 이미지가 있기 때문이다.
# 같은 column은 같은 종류의 이미지를 의미한다.k=1일 때 예측하기
# predict_lables() 구현하기
# Now implement the function predict_labels and run the code below:
# We use k = 1 (which is Nearest Neighbor).
y_test_pred = classifier.predict_labels(dists, k=1)
# Compute and print the fraction of correctly predicted examples
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))predict_labels 함수
def predict_labels(self, dists, k=1):
"""
Given a matrix of distances between test points and training points,
predict a label for each test point.
Inputs:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
gives the distance betwen the ith test point and the jth training point.
Returns:
- y: A numpy array of shape (num_test,) containing predicted labels for the
test data, where y[i] is the predicted label for the test point X[i].
"""
num_test = dists.shape[0]
y_pred = np.zeros(num_test)
for i in range(num_test):
# A list of length k storing the labels of the k nearest neighbors to
# the ith test point.
closest_y = []
#########################################################################
# TODO: #
# Use the distance matrix to find the k nearest neighbors of the ith #
# testing point, and use self.y_train to find the labels of these #
# neighbors. Store these labels in closest_y. #
# Hint: Look up the function numpy.argsort. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# dists[i].argsort()[:k] : i번째 테스트 데이터와 가까운 k개의 훈련 데이터의 인덱스
closest_y = self.y_train[np.argsort(dists[i])[:k]]
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
#########################################################################
# TODO: #
# Now that you have found the labels of the k nearest neighbors, you #
# need to find the most common label in the list closest_y of labels. #
# Store this label in y_pred[i]. Break ties by choosing the smaller #
# label. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# np.bincount() : 각 숫자가 몇 번 나왔는지 세어줌
# np.argmax() : 가장 큰 값의 인덱스를 반환
y_pred[i] = np.argmax(np.bincount(closest_y))
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return y_pred27%의 정확도가 나왔다.
Got 137 / 500 correct => accuracy: 0.274000
k=5일 때 예측
y_test_pred = classifier.predict_labels(dists, k=5)
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))
# L1 distance는 각 원소의 차이를 더한다, 상대적으로 덜 중요한 값을 무시할 수 있다(?)
# inline question2 잘 모르겠다....k=1일 때 보다 나은 결과를 보여준다.
Got 139 / 500 correct => accuracy: 0.278000
two_loops, one_loop, no_loop로 예측
# Let's compare how fast the implementations are
def time_function(f, *args):
"""
Call a function f with args and return the time (in seconds) that it took to execute.
"""
import time
tic = time.time()
f(*args)
toc = time.time()
return toc - tic
two_loop_time = time_function(classifier.compute_distances_two_loops, X_test)
print('Two loop version took %f seconds' % two_loop_time)
one_loop_time = time_function(classifier.compute_distances_one_loop, X_test)
print('One loop version took %f seconds' % one_loop_time)
no_loop_time = time_function(classifier.compute_distances_no_loops, X_test)
print('No loop version took %f seconds' % no_loop_time)
# You should see significantly faster performance with the fully vectorized implementation!
# NOTE: depending on what machine you're using,
# you might not see a speedup when you go from two loops to one loop,
# and might even see a slow-down.
# 사용하는 기기에 따라서 속도가 다를 수 있다. 오히려 더 낮아질 수 있다.
# two loop
# dists[i, j] = np.sqrt(np.sum(np.square(X[i] - self.X_train[j])))
# one loop
# dists[i, :] = np.sqrt(np.sum(np.square(np.tile(X[i], (num_train, 1)) - self.X_train), axis=1))
# no loop
# dists = np.sqrt(-2 * np.dot(X, self.X_train.T) + np.sum(np.square(self.X_train), axis=1) + np.transpose([np.sum(np.square(X), axis=1)]))one_loop 함수
def compute_distances_one_loop(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a single loop over the test data.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
#######################################################################
# TODO: #
# Compute the l2 distance between the ith test point and all training #
# points, and store the result in dists[i, :]. #
# Do not use np.linalg.norm(). #
#######################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# np.tile() : array를 반복해서 생성
# np.sum() : 합
# np.sqrt() : 제곱근
dists[i, :] = np.sqrt(np.sum(np.square(np.tile(X[i], (num_train, 1)) - self.X_train), axis=1))
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return distsno_loop 함수
def compute_distances_no_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using no explicit loops.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
#########################################################################
# TODO: #
# Compute the l2 distance between all test points and all training #
# points without using any explicit loops, and store the result in #
# dists. #
# #
# You should implement this function using only basic array operations; #
# in particular you should not use functions from scipy, #
# nor use np.linalg.norm(). #
# #
# HINT: Try to formulate the l2 distance using matrix multiplication #
# and two broadcast sums. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dists = np.sqrt(-2 * np.dot(X, self.X_train.T) + np.sum(np.square(self.X_train), axis=1) + np.transpose([np.sum(np.square(X), axis=1)]))
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return distsTwo loop version took 14.501467 seconds
One loop version took 20.383668 seconds
No loop version took 0.188824 seconds
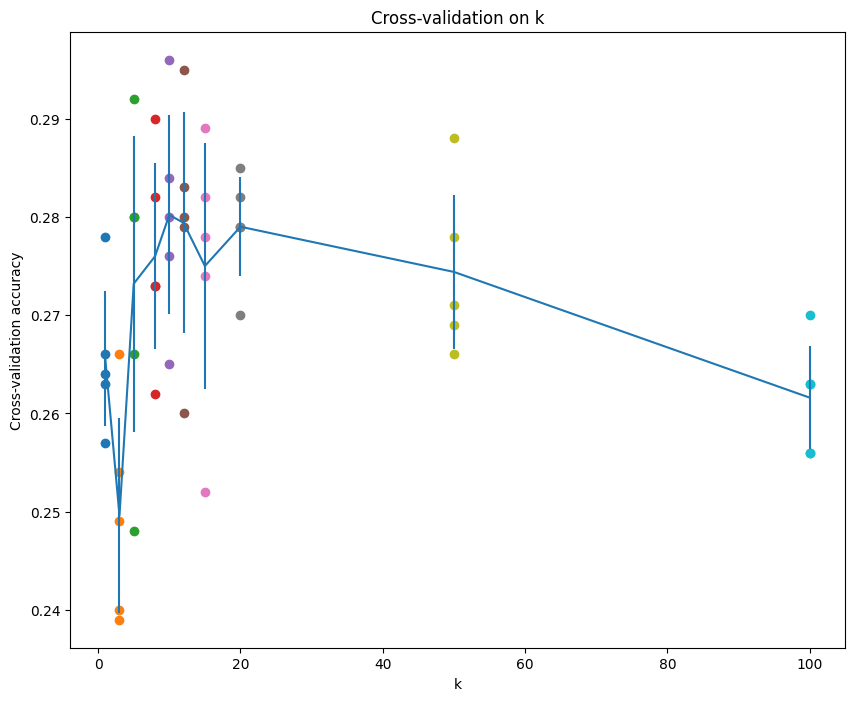
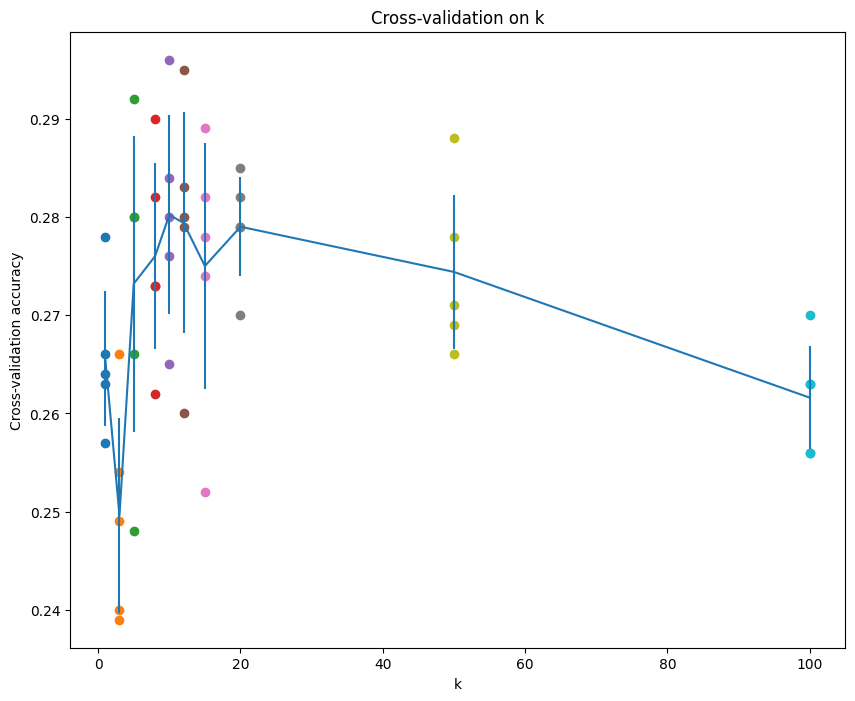
5-fold cross-validation
1~4는 train set, 5는 validation set으로 파라미터 튜닝에 사용됨, 이후 교차검증을 통해 어떤 fold를 사용할지 정하고, test data를 통해 평가한다.

교차검증(cross-validation)
# 교차검증을 통해 가장 최적의 k 값을 찾아 낸다.
num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]
X_train_folds = []
y_train_folds = []
################################################################################
# TODO: #
# Split up the training data into folds. After splitting, X_train_folds and #
# y_train_folds should each be lists of length num_folds, where #
# y_train_folds[i] is the label vector for the points in X_train_folds[i]. #
# Hint: Look up the numpy array_split function. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
range_split = np.array_split(range(X_train.shape[0]), num_folds)
y_train_folds = [ y_train[range_split[i]] for i in range(num_folds)]
X_train_folds = [ X_train[range_split[i]] for i in range(num_folds)]
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}
################################################################################
# TODO: #
# Perform k-fold cross validation to find the best value of k. For each #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times, #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all #
# values of k in the k_to_accuracies dictionary. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
for k in k_choices:
for fold in range(num_folds): #This fold will be omitted.
#Creating validation data and temp training data
validation_X_test = X_train_folds[fold]
validation_y_test = y_train_folds[fold]
temp_X_train = np.concatenate(X_train_folds[:fold] + X_train_folds[fold + 1:])
temp_y_train = np.concatenate(y_train_folds[:fold] + y_train_folds[fold + 1:])
#Initializing a class
test_classifier = KNearestNeighbor()
test_classifier.train(temp_X_train, temp_y_train)
#Computing the distance
temp_dists = test_classifier.compute_distances_two_loops(validation_X_test)
temp_y_test_pred = test_classifier.predict_labels(temp_dists, k=k)
#Checking accuracies
num_correct = np.sum(temp_y_test_pred == validation_y_test)
num_test = validation_X_test.shape[0]
accuracy = float(num_correct) / num_test
print("k=",k,"Fold=",fold,"Accuracy=",accuracy)
k_to_accuracies[k] = k_to_accuracies.get(k,[]) + [accuracy]
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Print out the computed accuracies
for k in sorted(k_to_accuracies):
for accuracy in k_to_accuracies[k]:
시각화
# plot the raw observations
for k in k_choices:
accuracies = k_to_accuracies[k]
plt.scatter([k] * len(accuracies), accuracies)
# plot the trend line with error bars that correspond to standard deviation
accuracies_mean = np.array([np.mean(v) for k,v in sorted(k_to_accuracies.items())])
accuracies_std = np.array([np.std(v) for k,v in sorted(k_to_accuracies.items())])
plt.errorbar(k_choices, accuracies_mean, yerr=accuracies_std)
plt.title('Cross-validation on k')
plt.xlabel('k')
plt.ylabel('Cross-validation accuracy')
plt.show()best_k로 test case 돌려보기
# Based on the cross-validation results above, choose the best value for k,
# retrain the classifier using all the training data, and test it on the test
# data. You should be able to get above 28% accuracy on the test data.
best_k = k_choices[np.argmax(accuracies_mean)]
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
y_test_pred = classifier.predict(X_test, k=best_k)
# Compute and display the accuracy
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))kNN으로는 이 데이터셋을 잘 분류하기 어렵다..
Got 141 / 1000 correct => accuracy: 0.141000
kNN은 낮은 cost를 가지지만 고차원(이미지) 데이터에서 직관적이지 않을 수 있다.