개요
본 블로그 포스팅은 수도권 ICT 이노베이션 스퀘어에서 진행하는 AI 핵심 기술 집중 클래스의 자연어처리(NLP) 강좌 내용을 필자가 다시 복기한 내용에 관한 것입니다.
0.논문 살짝요약

이 논문은 24년 1월에 아카이브에 올라온 논문으로
RNN, GRU, LSTM와 같은 RNN계열의 언어모델이 현재의 대세 모델이라 볼 수 있는 Transformer에 밀려난 주요 단점인
1) 병렬 연산 및 학습 효율성 저하
2) 장기의존성 문제
중 1) 문제를 해결하기 위해
병렬 학습이 가능한 개선된 RNN 구조
인 miniLSTM, miniGRU 라는 모델을 제안한 논문이다.
Transformer는 기존의 순차연산으로만 처리되던 시퀀스 매트릭스를 Positional Encoding, Self-Attention 매커니즘 도입으로 병렬처리가 가능해져 기존 언어모델의 대표라 볼 수 있는 RNN계열 모델을 밀어내고 나아가 현재 대다수 딥러닝 API의 주요 Backbone으로 사용되고 있다.
논문에서 제안한 miniLSTM, miniGRU은 현재 시점의 state를 계산 하기 위해서는 이전 시점의 상태에 의존하는 '순환적 의존성(Recurrent Dependency)'을 제거하여 시퀀스 데이터셋이 입력되더라도 모든 시점에 대해 병렬 처리가 가능한
병렬 스캔 알고리즘을 적용했다.
따라서 논문에서는 제안한 방법론을 통해
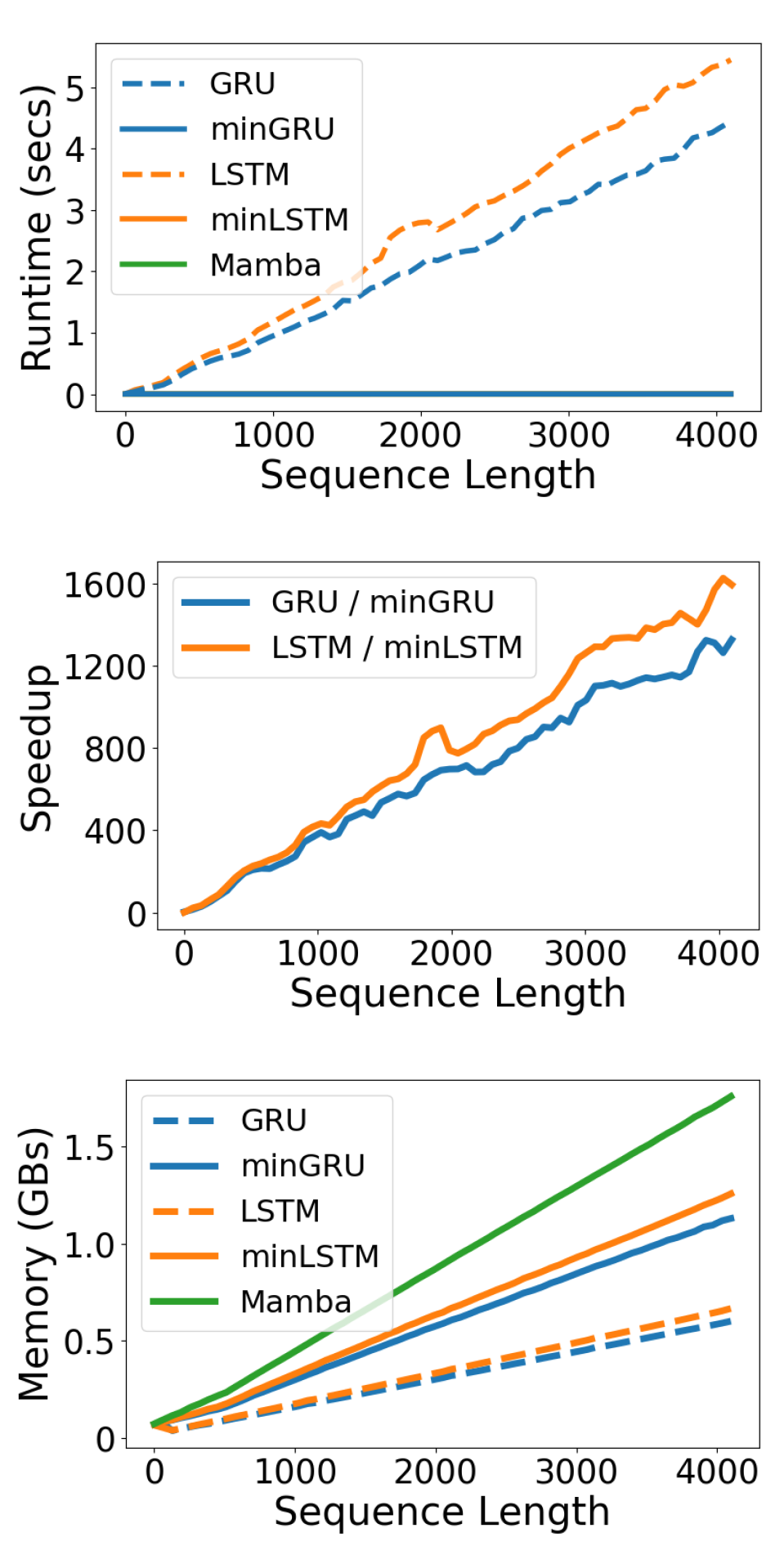
위 사진처럼 시퀀스 데이터의 길이가 길어져도
다른 기존 순차연산 방식의 RNN계열 모델에 비해
실행속도가 영향 받지 않는 장점이 있다.
물론 제안한 miniLSTM, miniGRU는
병렬 스캔 알고리즘이 적용되기에 모든 시점에 대한 중간 결과물을 저장 -> 이로 인한 메모리 사용량이 증가되는 단점이 있다.
여기서 비교군으로 Mamba 모델을 선정했는데
필자는 해당 모델에 대해 자세하게 학습하지는 못했지만 Transformer이 긴 시퀀스 처리에서는 계산 비효율성이 높아지며, 이를 개선한 모델이 Mamba이라 한다.
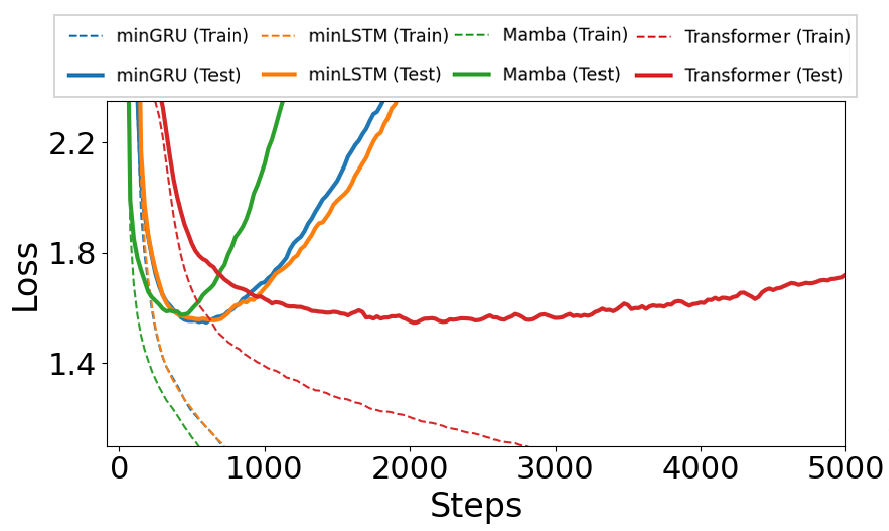
그러나 모델별 훈련/검증 손실 지표를 본다면
모델의 훈련 모드 / 검증 단계의 괴리가 발생하는 과적합 도달 구간이 miniLSTM, miniGRU가 Transformer보다 빠르게 도달하는 것을 본다면
모델의 일반화 성능은 Transformer을 따라잡지는 못하는 것을 확인 할 수있다.
하지만 Were RNNs All We Needed? 논문은
1) RNN계열의 모델이라도 병렬처리가 가능함을 입증
2) Transformer와의 성능 격차를 축소하려 시도함
과 같은 '가능성'을 제시한 논문이라 볼 수 있다.
0.1 논문 선정 이유
이 논문은 올해 출시된 최신논문이기에 별로 다뤄진 사례가 없긴하지만 흥미가 있어서 포스팅을 진행한다.
주요 이유로는
⭐ 논문을 이해하려면 RNN, GRU, LSTM을 수식적으로 정리를 온전히 마쳐야 하며, 로우 레벨 프로그래밍 까지 진행해야함
⭐ miniLSTM, miniGRU의 코드구현(Pytorch)은 자료를 찾아보니 그렇게 난이도가 높은 편은 아님
⭐ 결국 CNN과 같은 가장 기초 레이어에 대한 탐구이기에 이전 포스트
2. NLP-LSTM, GRU (2) : 텍스트 분류기의
텍스트 분류기-RNN, LSTM, GRU 기반 모델과
비교분석 리포트 작성이 용이함
이렇게 정리하는게 가능할 듯 하다.
물론 포스트에 사용한 데이터셋
https://github.com/tbvjvsladla/ASH_NLP_lacture/blob/main/spam_SNS.csv
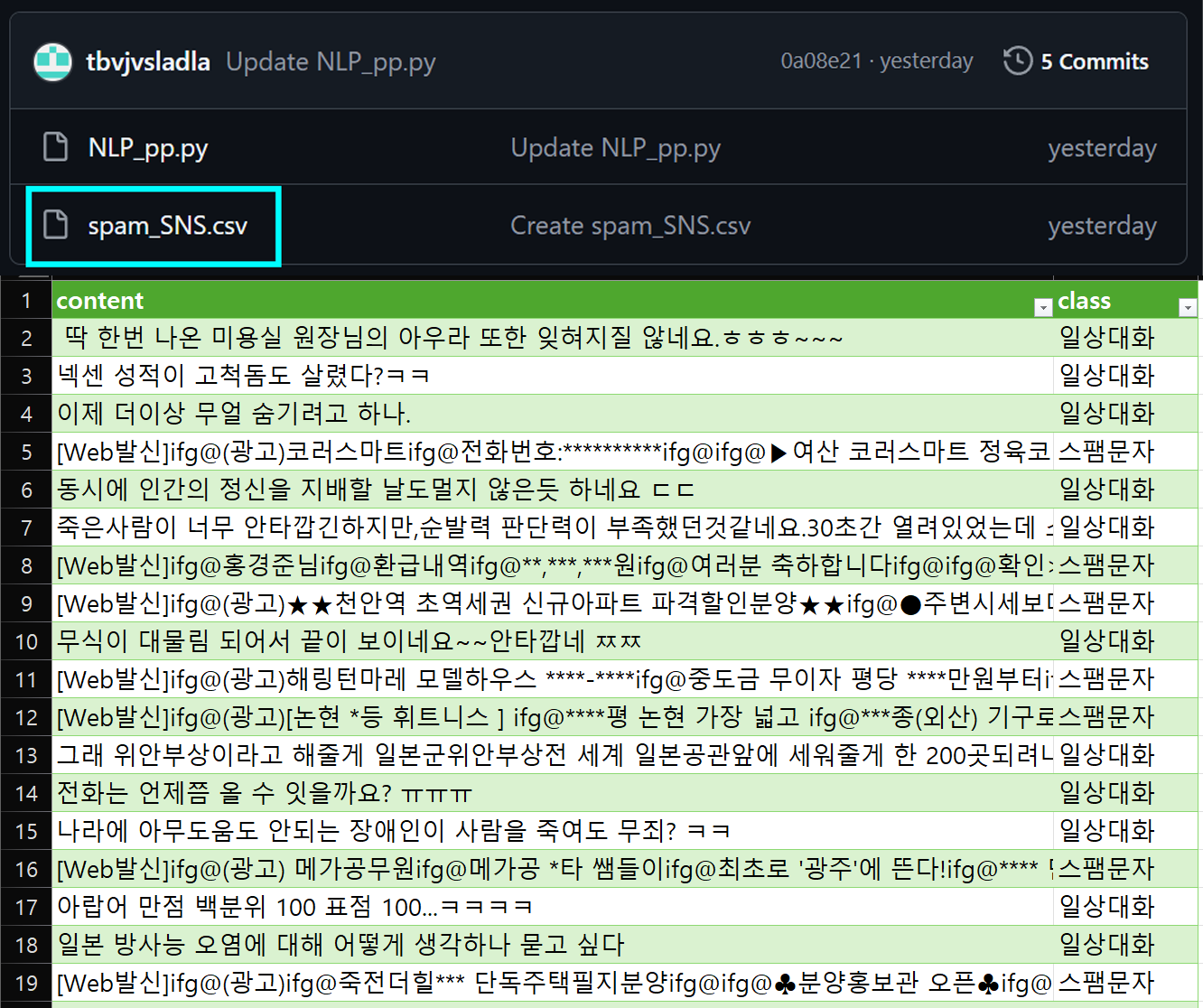
은 시퀀스 길이도 문장패딩을 적용시 300 토큰 정도고 데이터양도 그리 많은 편은 아니지만
향후 Seq2Seq를 소개할 때 backbone로 활용하면 재미있는 결과를 얻을 수 있을 것 같아서
미리 포스팅을 진행하고자 한다.
0.2 사전지식 - RNN,LSTM,GRU
RNN 로우 레벨 프로그래밍
먼저 RNN의 수식을 다시한번 살펴보도록 하겠다.

은닉상태 의 연산에는 입력 와 이전 은닉상태 에 의존하기에 이 이 병렬처리를 불가능하게 하는 주요 원인이자 RNN계열 언어모델의 주요 특징이다.
이를 nn.RNN메서드가 아닌 nn.Module클래스를 상속받는 형식으로 로우레벨 프로그래밍 해보자.
import torch
import torch.nn as nnclass RNNCell(nn.Module):
def __init__(self, in_ch, out_ch):
super(RNNCell, self).__init__()
self.linear = nn.Linear(in_ch, out_ch)
self.tanh = nn.Tanh()
def forward(self, x):
x = self.linear(x)
x = self.tanh(x)
return xclass RawRNN (nn.Module):
def __init__(self, input_size, hidden_size, num_layers=1):
super(RawRNN, self).__init__()
# 주요 RNN설계 파라미터를 먼저 선언
self.hidden_size = hidden_size
self.num_layers = num_layers
# RNN 셀은 중간 데이터를 추출하는 과정이 있기에
# 셀이 여렇게 쌓이더라도 nn.Sequential이 아닌
# nn.ModuleList로 처리해야함
self.cells = nn.ModuleList([
# 셀이 여러개 쌓이면 맨 첫번째 층은 input_size
# 그 다음 층부터는 hidden_size가 입력되는 구조임
RNNCell(input_size if i == 0 else hidden_size,
hidden_size)
for i in range(num_layers)
])
def forward(self, x, hidden=None):
# 입력되는 x는 batch_first=True 인 상태로만 입력된다.
# x차원 : Batch_size, context_length, embedding_dim
bs, seq_len, _ = x.size()
# hidden 정보가 없으면 zeros로 차원에 맞게 생성함
if hidden is None:
hidden = torch.zeros(self.num_layers, bs, self.hidden_size,
device=x.device, dtype=x.dtype)
y_t = []
h_t = hidden
for t in range(seq_len):
# 입력된 x에서 t번째 seq 정보만 추출
x_t = x[:, t, :]
for layer in range(self.num_layers):
# 셀의 개수가 1개 이면 x_t만 입력되는 구조
h_t[layer] = self.cells[layer](x_t if layer == 0
else h_t[layer-1])
y_t.append(h_t[-1])
# 스택이 쌓이면 출력 y는 (Batch_size, context_length, hid_dim)
output = torch.stack(y_t, dim=1)
return output, h_t위 RNN 수식과 이를 코드화 하는 것을 연습해야
이후 진행할 LSTM, GRU를 코드화 하는데 어려움이 없다.
LSTM 로우 레벨 프로그래밍
다음으로 LSTM의 구조를 수식과 같이 매칭하여 분석한 뒤
이를 로우 레벨 프로그래밍을 수행하도록 하겠다.
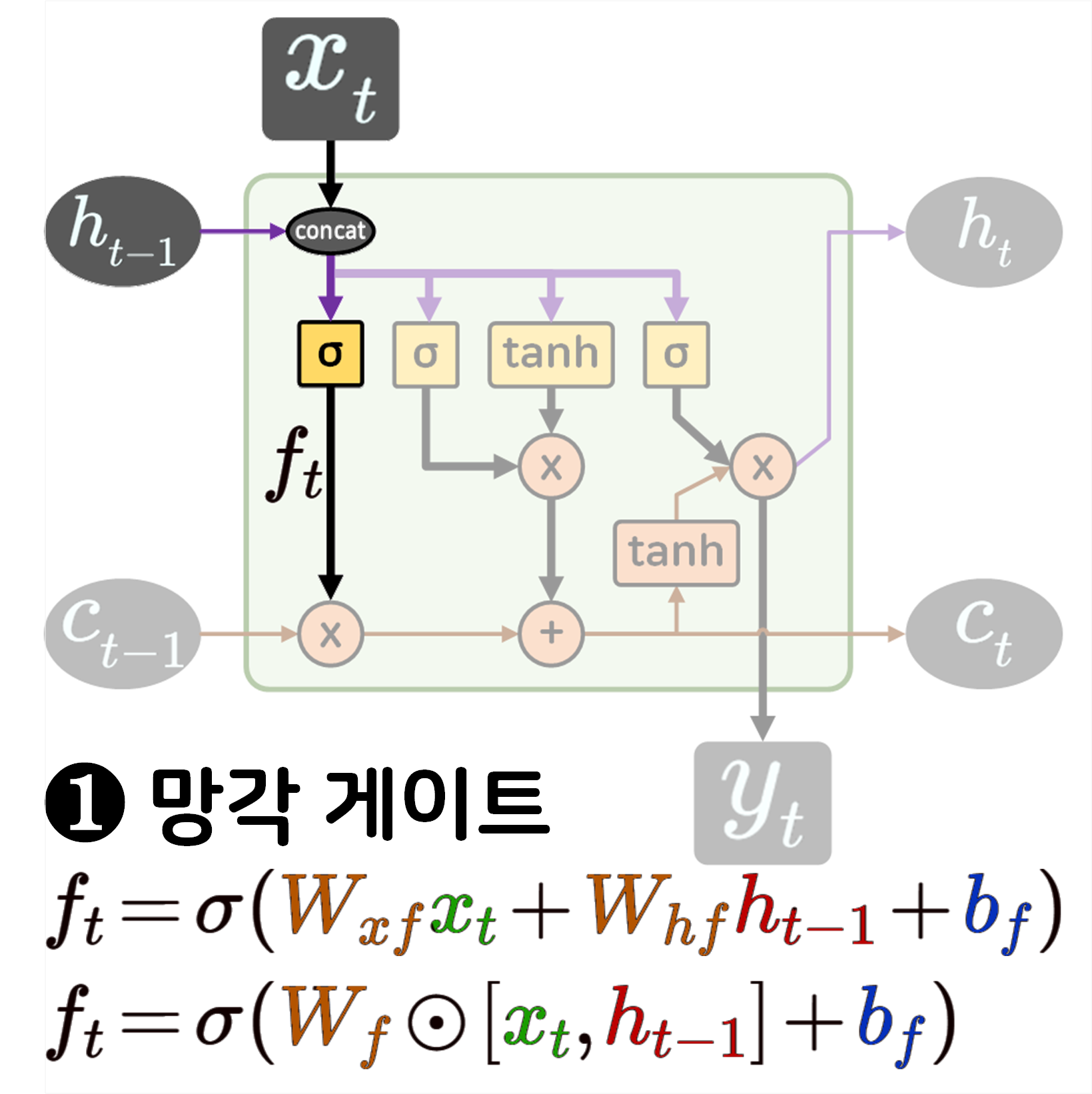
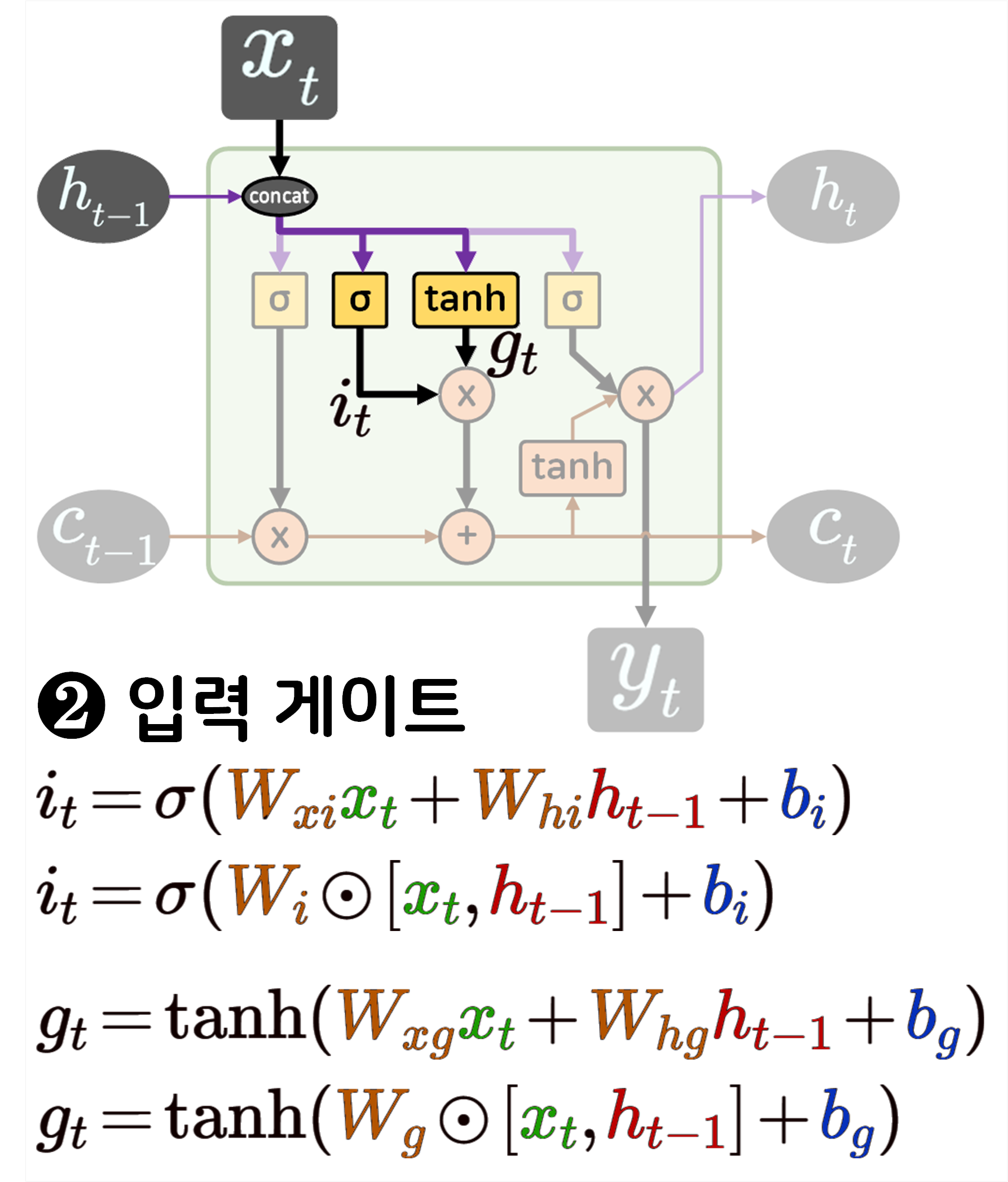
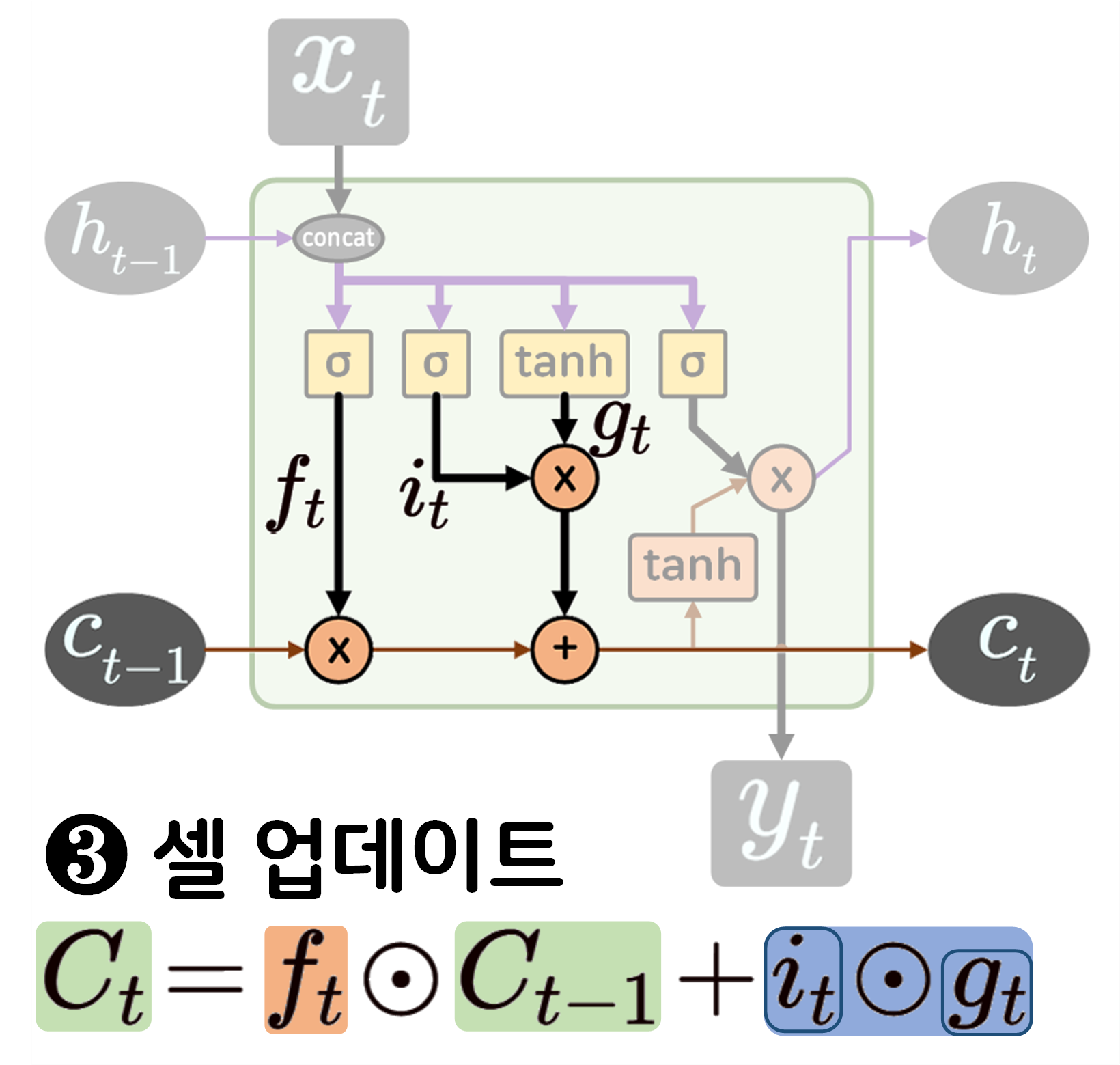
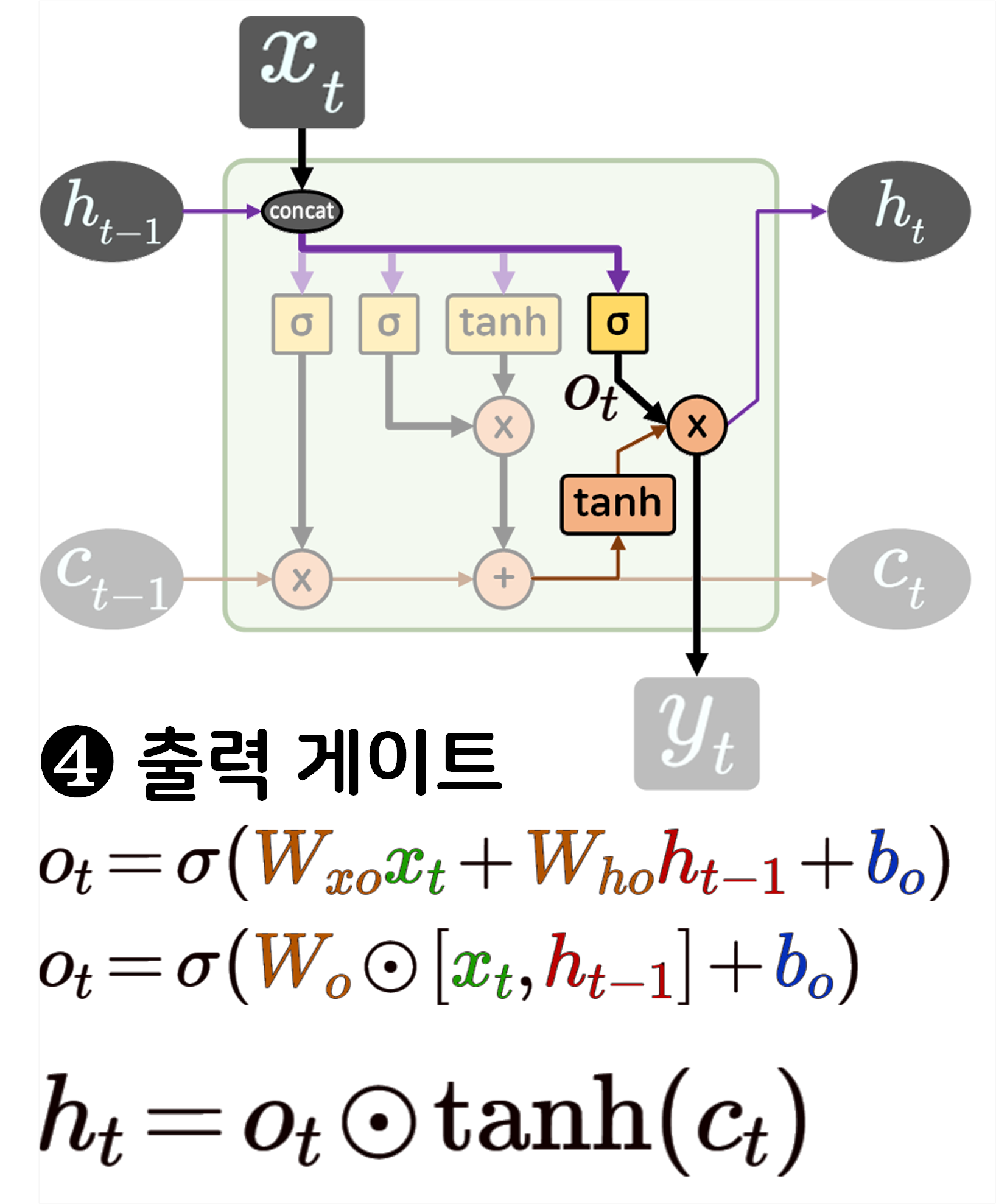
class RawLSTM(nn.Module):
def __init__(self, input_size, hidden_size, num_layers=1):
super(RawLSTM, self).__init__()
# 주요 설계 파라미터를 먼저 선언
self.hidden_size = hidden_size
self.num_layers = num_layers
# LSTM cell은 linear 한층만 생성자에 넣음
self.cells = nn.ModuleList([
# 셀이 여러개 쌓이면 맨 첫층만 input(x)
# 그 다음층부터는 hidden층 입력이 들어감
nn.Linear(input_size if i == 0 else hidden_size,
hidden_size * 4)
#출력이 4개(게이트 개수)로 나옴
for i in range(num_layers)
])
def forward(self, x, hidden=None):
bs, seq_len, _ = x.size()
if hidden is None:
h_t = torch.zeros(self.num_layers, bs, self.hidden_size,
device=x.device, dtype=x.dtype)
c_t = torch.zeros(self.num_layers, bs, self.hidden_size,
device=x.device, dtype=x.dtype)
else:
h_t, c_t = hidden
y_t = []
for t in range(seq_len):
# 입력 x는 seq단위로 분절함
x_t = x[:, t, :]
for layer in range(self.num_layers):
# 셀을 통과한 4개의 값을 gates로 저장
gates = self.cells[layer](x_t if layer == 0 else h_t[layer-1])
# gates 출력결과를 4개의 텐서로 균등하게 나누기
i_t, f_t, g_t, o_t = torch.chunk(gates, 4, dim=-1)
f_t = torch.sigmoid(f_t) #망각 게이트
i_t = torch.sigmoid(i_t) #입력 게이트_1
g_t = torch.tanh(g_t) #입력게이트_2
o_t = torch.sigmoid(o_t) #출력게이트
# 셀 상태 업데이트 연산 수행
c_t[layer] = f_t*c_t[layer] + i_t*g_t
# 은닉 상태 업데이트 수행
h_t[layer] = o_t * torch.tanh(c_t[layer])
y_t.append(h_t[-1])
output = torch.stack(y_t, dim=1)
return output, (h_t, c_t)GRU 로우 레벨 프로그래밍
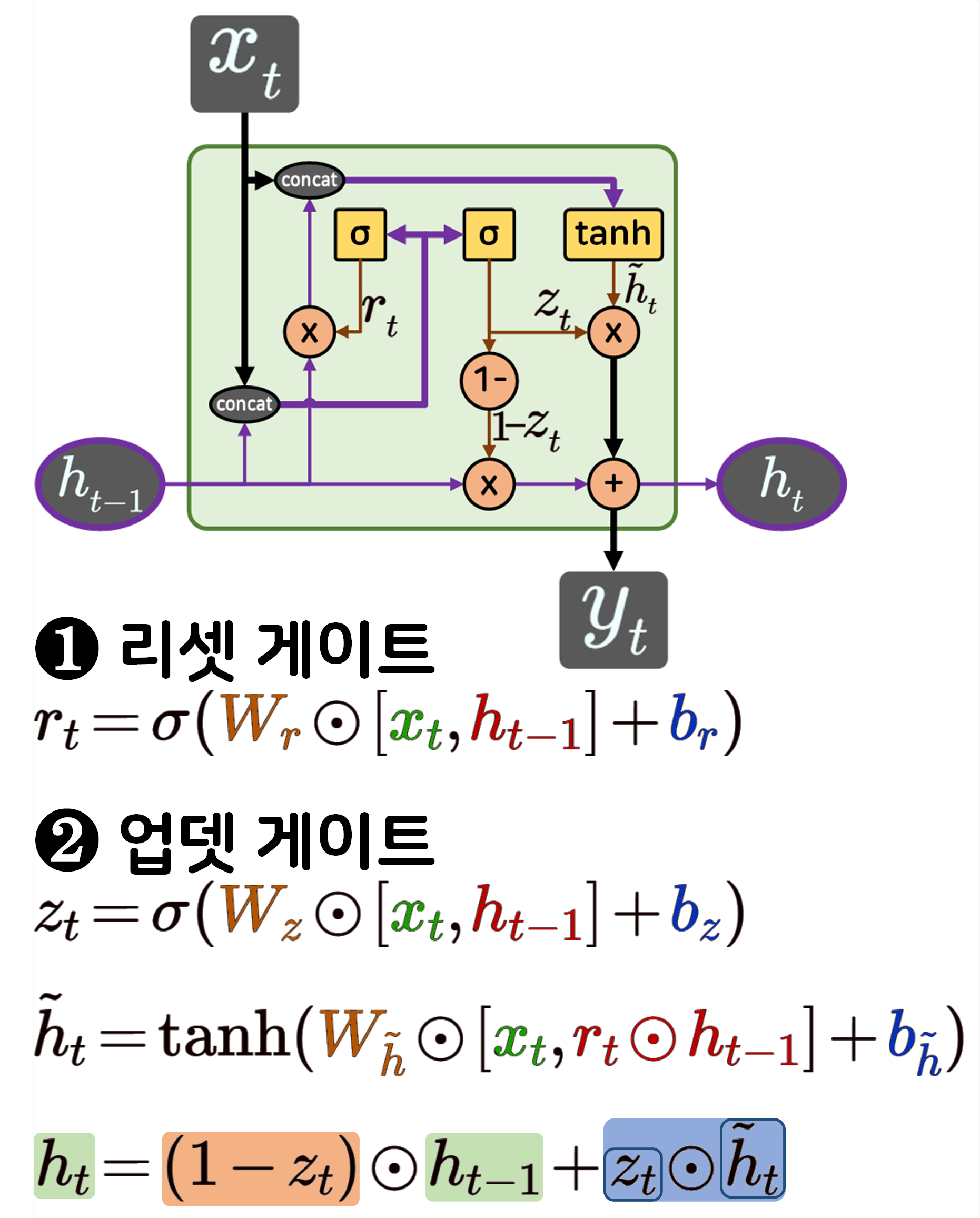
class RawGRU(nn.Module):
def __init__(self, input_size, hidden_size, num_layers=1):
super(RawGRU, self).__init__()
# 주요 설계 파라미터를 먼저 선언
self.hidden_size = hidden_size
self.num_layers = num_layers
# GRU cell은 LSTM이랑 구조가 같으나, 게이트가 1개 적음
self.cells = nn.ModuleList([
nn.Linear(input_size if i == 0 else hidden_size,
hidden_size * 3)
for i in range(num_layers)
])
def forward(self, x, hidden=None):
bs, seq_len, _ = x.size()
if hidden is None:
h_t = torch.zeros(self.num_layers, bs, self.hidden_size,
device=x.device, dtype=x.dtype)
else:
h_t = hidden
y_t = []
for t in range(seq_len):
x_t = x[:, t, :]
for layer in range(self.num_layers):
gates = self.cells[layer](x_t if layer == 0 else h_t[layer-1])
r_t, z_t, h_t_tilt = torch.chunk(gates, 3, dim=-1)
r_t = torch.sigmoid(r_t)
z_t = torch.sigmoid(z_t)
h_t_tilt = torch.tanh(h_t_tilt + r_t*h_t[layer])
#은닉 상태 업데이트 수행
h_t[layer] = (1 - z_t)*h_t[layer] + z_t*h_t_tilt
y_t.append(h_t[-1])
output = torch.stack(y_t, dim=1)
return output, h_t위 3가지 RNN 계열 모델에 대한 수식 정리 + 로우 레벨 프로그래밍을 사전에 수행했으니
이제 본격적으로 Were RNN All We Needed? 논문에 대한 리뷰를 진행하도록 하겠다.
1. Were RNN All We Needed?
논문의 초록에서 지적하는 내용은 Transformer계열의 모델은 시퀀스 길이에 대한 확장성 한계가 발생한다 언급하고 있으며,
이는 Transformer계열 모델이 필수적으로 수행하는 Self-Attention으로 인한 계산 복잡도의 증가와 메모리 사용량의 증가를 언급하는 듯 하다
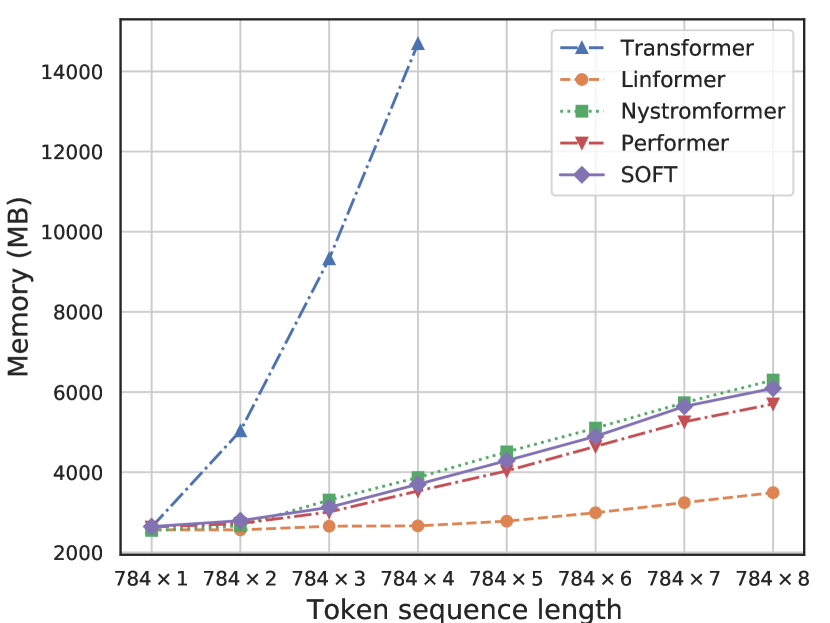
이는 다른 논문에서 발췌한 사진으로 Transformer계열 모델은 타 모델에 비해 시퀀스 길이가 긴 데이터에 관해서는 소비되는 메모리양이 급격하게 늘어나는 것을 알 수 있다.
이로인해 S4, Mamba, Aaren 같은 순환 아키텍쳐 기반의 모델이 제안되었다 언급하고 있다.
그러나 위 모델들은 각각 나름의 한계점이 있어 Transformer를 완전히 대체하지는 못하고 있다.
이에 논문의 저자들은 이제는 거의 사장되다 싶이한 언어모델인 RNN계열의 모델을 개선하여 Transformer를 대체하고자 시도한 논문이 Were RNN All We Needed?이다.
논문에서 제시하는 miniLSTM, miniGRU는 공통적으로 기존의 LSTM, GRU 대비 파라미터의 개수가 적은 장점도 있지만 가장 중요한 개선점은
⭐ 역전파 과정에서 이전 은닉 상태 의 의존성을 제거해 시간 기반 역전파(BPTT : backpropagate through time)를 수행하지 않아도 됨 훈련을 진행할 때 완전 병렬화가 가능
즉 훈련 과정에서 발생하는 순차과정이 모두 병렬수행이 가능해져 빠르게 학습이 가능하다
이것이 miniLSTM, miniGRU에서 제시된 가장 큰 개선사항이라 볼 수 있다.
실험결과 기존 LSTM, GRU에 비해 175배 빠르게 학습이 가능하다 논문에서 소개하고 있으니 어떻게 이를 구현했는지 알아보고자 한다.
병렬 접두사 스캔 알고리즘(parallel prefix scan)
앞서 LSTM, GRU은 순환연산으로 인해 병렬화 학습이 불가능하고
학습또한 비 효율적이라 볼 수 있는 BPTT기반 역전파가 수행됨을 알 수 있다.
이 한계를 극복한게 Transformer이고 Positional encoding 및 self-attntion 알고리즘의 도입으로 해결했다.
물론 논문에서는 위 방법론이 시퀀스 길이에 대하여 이차적인 복잡도(quadratic complexity) 문제를 가져왔고, 이때문에 Transformer는 나름의 한계점이 있기에
연구자들은 BPTT문제를 해결하기 위한 방법론으로
parallel prefix scan을 제안하고 있다.
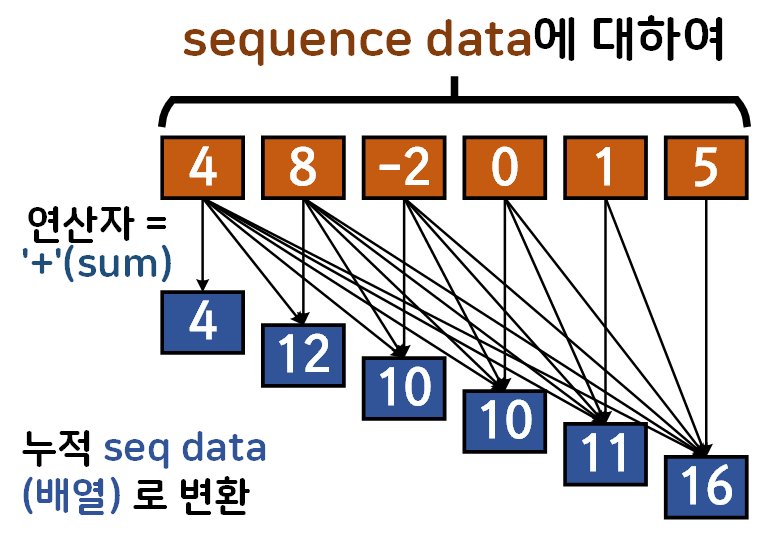
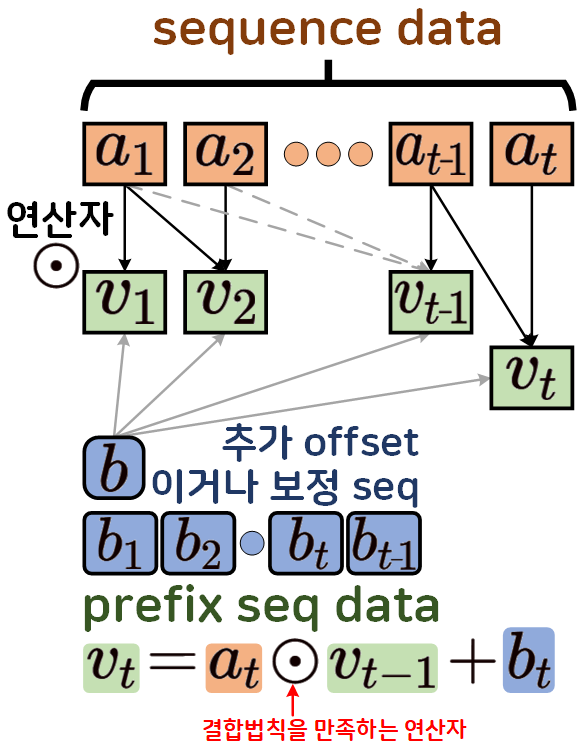
위 도식이 parallel prefix scan의 첫번째 연산 과정으로
기존의 Sequence data를 연산자가 하나 지정되어 있다면
해당 연산자를 바탕으로 누적 연산을 수행
prefix seq data로 변환을 수행하고
해당 데이터를 활용하는게 parallel prefix scan 알고리즘의 장점이라 볼 수 있다.
여기서 중요한 것은 연산자는 무조건 '연관적(associative)'이어야 한다는 것이다.
이 '연관적(associative)'이란 조건을 충족하려면
결합법칙을 만족하는 연산자면 된다.

위 결합법칙을 만족하는 연산자는
덧셈, 곱셈, 최대&최소값, 비트연산(OR, AND, XOR)등이 존재한다.
따라서 위 연산자 이미지를 곱셈으로 변환하면 아래의
prefix seq data를 얻어낼 수 있다.
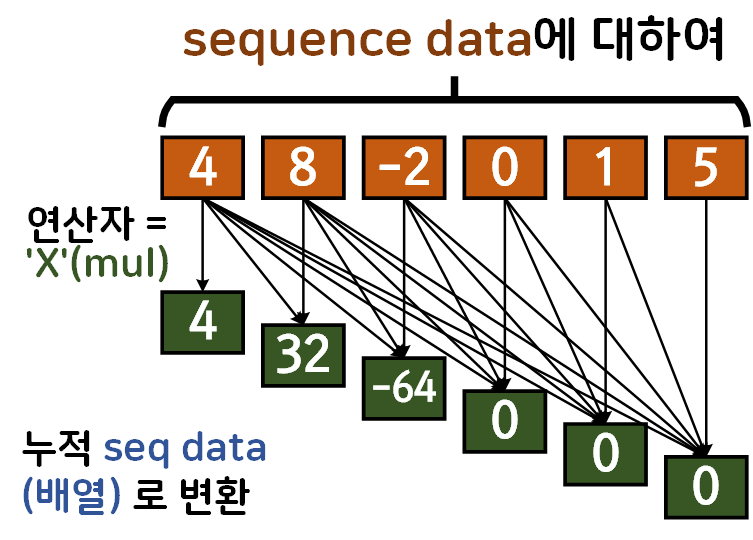

그러나 어떠한 연산자에 대해 Seq data prefix seq data로 변환하는것이
scan 작업에 어떤 효용성을 갖는지 확인하려면
코딩테스트 문제를 풀어봐야 한다...

이 문제를 풀면 어느정도 감이 잡히는데
먼저 가장 시간복잡도가 높은 방식으로 문제를 풀이하도록 하겠다.
import numpy as np
N = 100000 #순차 배열을 만들기 위한 값
seq = np.arange(1, N+1) #1~N까지 순차 배열 생성
# A번째 숫자와 B번째 숫자를 정의
A, B = 500, 20000위와 같이 문제에 대한 배경값을 설정한 뒤
# 계산 복잡도가 가장 높은 순차적으로 연산수행
# 이 연산의 경우 시간복잡도가 O(N)
def Rec_op(A, B, seq):
# A가 B보다 크면 스위칭 수행
if A > B :
A, B = B, A
split_seq = seq[A-1:B]
result = 0
for i in split_seq:
result += i
return result순차 방식으로 연산을 수행하는 코드를 작성하면
위 함수의 시간 복잡도는 이 된다.
하지만 이를 prefix seq data를 생성하여 parallel prefix scan 과정을 수행하면
# 맨 처음 누적배열을 생성하는데만 시간이 소요됨
pre_seq = []
for idx, vel in enumerate(seq):
if idx == 0:
pre_seq.append(vel)
else :
temp = pre_seq[idx-1] + vel
pre_seq.append(temp)
pre_seq = np.array(pre_seq)
#위 코드는 np.cumsum(seq)로 라이브러리 써서 한번에 구현 가능
# 누적 배열을 생성 후 연산 수행
# 이 연산은 시간 복잡도가 O(1)
def prefix_op(A, B, pre_seq):
# A가 B보다 크면 스위칭 수행
if A > B :
A, B = B, A
if A == 1:
return pre_seq[B-1]
else:
return pre_seq[B-1] - pre_seq[A-2]맨 첫 회만 prefix seq data 만들어 내면 매 회 부분 합(연산) 결과를 추출(scan)하는데
시간 복잡도는 이 된다.
여기서 prefix seq data를 생성하는 과정 또한 GPU연산 과정을 사용하면 더 빠르게 수행할 수 있다.
import cupy as cp
# 누적 배열 생성을 GPU연산으로 빠르게 생성
pre_seq = cp.cumsum(cp.array(seq))여기서 cp.cumsum는 np.cumsum 대비 더 빠르게
prefix seq data를 생성하는데
이대 사용되는 방법론이 Up-sweep & Down-sweep Phase 이다.
음.. 이거는 잘 이해가 안가긴 한데
처음 prefix seq data 를 생성하는것도 따지고 보면 순차 누적 연산이기에 시간 복잡도는 이지만
GPU병렬처리가 가능한 Up-sweep & Down-sweep Phase를 적용하면
시간 복잡도가 으로 줄어든다... 이렇게 보면 된다.
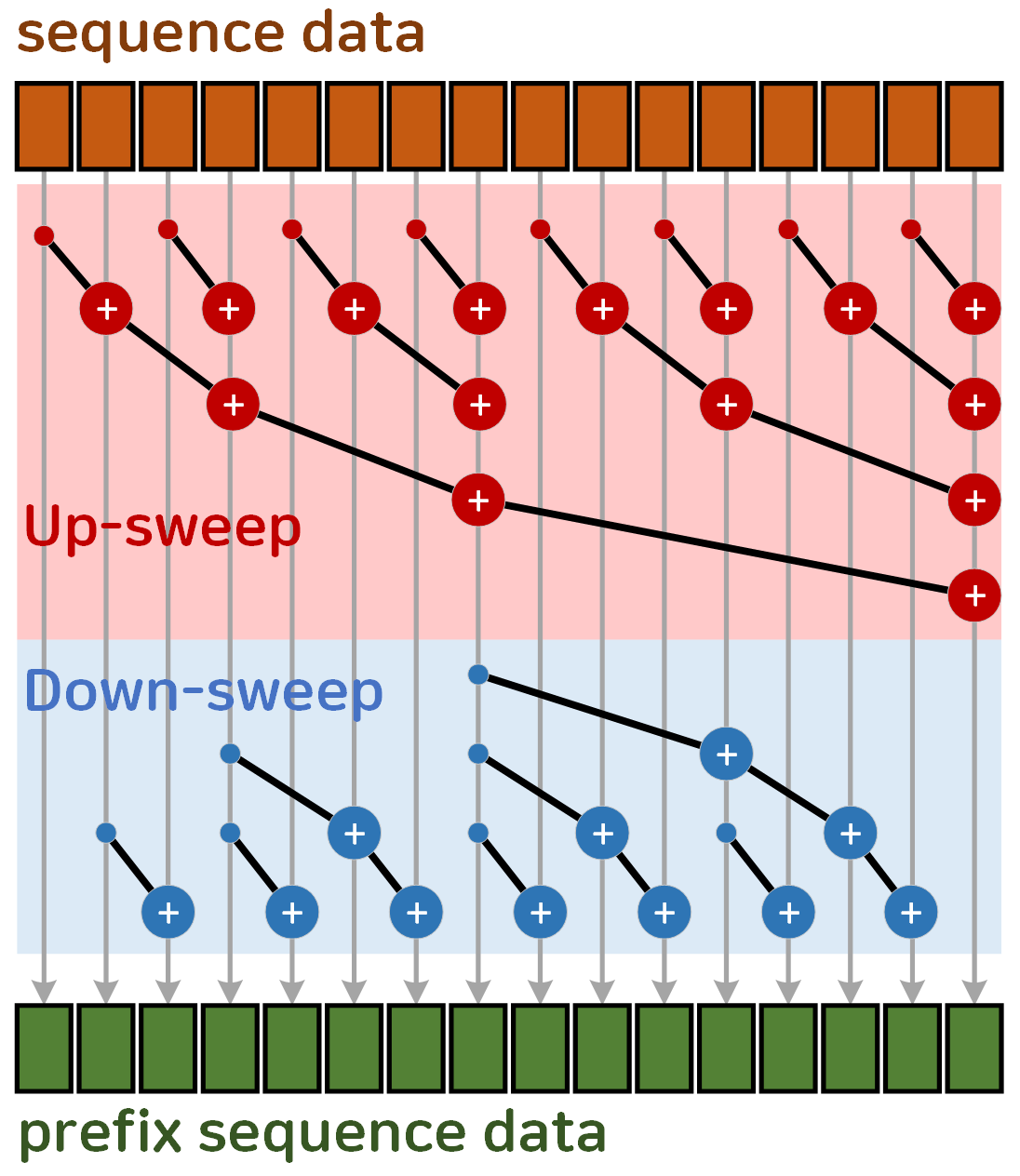
음.. 아무튼 위 사진으로 살펴본다면
초기 Seq data 는 Up-sweep Down-sweep 과정을 거쳐
prefix seq data로 변화하는데 이때
기존의 순차 방식 Seq data prefix seq data 보다 시간 복잡도도 줄어들고
GPU 병렬처리 연산도 가능하다는게
Up-sweep & Down-sweep Phase 라.. 보면 된다.
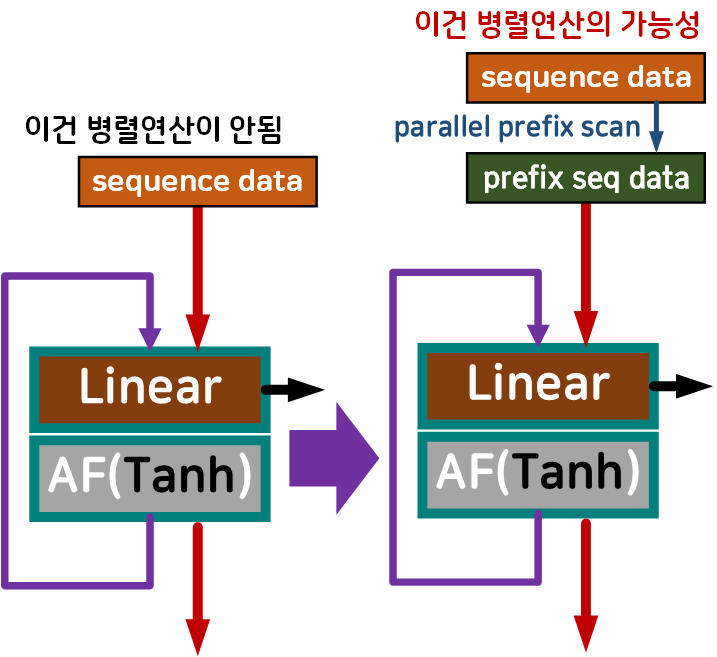
아무튼 정리를 하자면 parallel prefix scan를 도입해서 병렬 처리가 안되던 RNN계열 모델을 병렬 학습이 가능하게 만들자
이게 목적이라 보면 된다.
은닉 상태 간 의존성 삭제
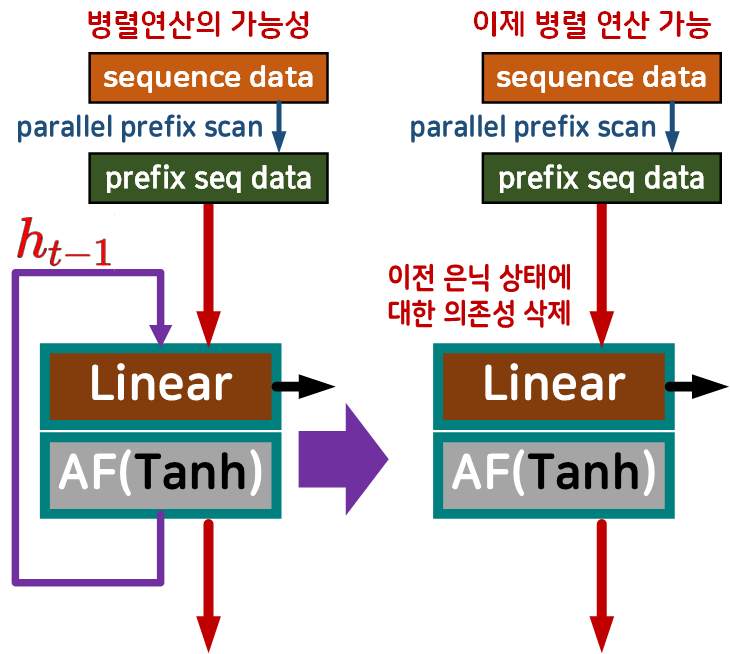
이제 위 사진처럼 LSTM, GRU에 이전 은닉 상태에 대한 의존성을 나타내는 인자값 항목을 없애면
prefix seq data 만으로 RNN계열의 모델 학습이 BPTT로부터 자유로워 지기에 병렬 처리로 가능해진다.
좀 더 정확하게는 이전 상태에 대한 누적 정보가 parallel prefix scan으로 인해 prefix seq data으로 모두 이전되니 이전 은닉 상태 를 필요 없는 인자로 만드는 것이 논문의 핵심이다 라고 볼 수 있다.
여기서 어떻게 의 정보가 parallel prefix scan방법론으로 대체되는지를 확인해야 하는데
LSTM, GRU의 수식이 prefix seq data를 생성하는 수식과 유사성이 있기에 대체가 가능하다
라고 생각하는것이 논문의 주 아이디어라 볼 수 있다.
따라서 GRU의 수식에서 의 정보가 prefix seq data로 대체되는지?
LSTM의 수식에서 의 정보가 prefix seq data로 대체되는지?
각각 확인하여 수식을 설계한 뒤 miniLSTM, miniGRU의 코드화를 수행해야 한다.
GRU의 정보를 prefix seq data를 적용한 수식 개선

prefix seq data를 생성하는 수식과 GRU의 수식 중 hidden 생성 수식을 비교하면 위 사진처럼 인자값 간의 유사성이 있다 판단하고 있으며,
논문에서는 와 의 수식에 정보와 의존성 정보가 포함된 이 존재하니 각각의 인자값들을 제거하는 작업을 수행한다.
논문에서는 게이트 간소화 및 수식 단순화 작업으로 각각의 정보들을 제거한 간단한 수식을 생성한다.

LSTM의 정보를 prefix seq data를 적용한 수식 개선

LSTM의 코드 간소화는 여러 단계를 거쳐서 진행된다


LSTM의 경우 miniLSTM로 코드간소화가 어떻게 진행되는지.. 조금 이해가 안가는 부분이 있긴 하지만
아무튼 최종 수식은 게이트가 4개에서 3개로 하나 줄어드는것은 확인이 가능하며, 논문에서는 GRU miniGRU 수식을 먼저 설명한 뒤 LSTM miniLSTM수식을 설명하고 있는데 이는
miniGRU의 수식을 생성하는 과정을 참조하여 miniLSTM 수식 생성을 수행하기에 쉬운 모델 먼저 설명이 진행되고 있다.
2. Implementaion Details
이제 Were RNN All We Needed? 논문에서 언급한 수식을 바탕으로 코드화를 수행하라고 하면
못한다

이게.. 깃 허브에서 자료를 찾아보면
https://github.com/MOVzeroOne/modernized_rnn
https://github.com/axion66/minLSTM-implementation
두 저장소에 구현된 코드가 있는데
못알아 먹겟다;;
그 이유는 논문의 부록을 살펴봐야 하기 때문이다.
논문의 부록 A, B 둘다 탐독을 해야 제대로 된 miniLSTM, miniGRU을 설계할 수 있으며
단계별로
1) parallel prefix scan를 적용하지 않고 miniLSTM, miniGRU를 설계하기
2) parallel prefix scan 를 적용한 버전 설계 + parallel prefix scan 함수 설계
3) 안정성 향상을 위한 디테일 코드 개선
이렇게 단계를 밟아가면서 코드 개발을 해야 쓸만한 miniLSTM, miniGRU을 사용할 수 있는것이다..
이제 논문의 부록을 참조하면서 설계를 진행하도록 하겠다
1) Sequential Mode miniGRU, miniLSTM 코드화

먼저 논문의 psudo code를 바탕으로 각각의 모델을 설계하도록 하겠다.
class MiniGRUSeq(nn.Module):
def __init__(self, input_size, hidden_size, num_layers=1):
super(MiniGRUSeq, self).__init__()
# 주요 설계 파라미터를 먼저 선언
self.hidden_size = hidden_size
self.num_layers = num_layers
# miniGRU는 게이트웨이가 간소화-> 2개
# 게이트웨이가 줄었으니 chunk로 분할하지 말고
# 그냥 게이트웨이별로 독립된 linear로 작성함
self.cells_z_t = nn.ModuleList([
nn.Linear(input_size if i == 0 else hidden_size, hidden_size)
for i in range(num_layers)
])
self.cells_h_tilde = nn.ModuleList([
nn.Linear(input_size if i == 0 else hidden_size, hidden_size)
for i in range(num_layers)
])
def forward(self, x, hidden=None):
bs, seq_len, _ = x.size()
if hidden is None:
h_t = torch.zeros(self.num_layers, bs, self.hidden_size,
device=x.device, dtype=x.dtype)
else:
h_t = hidden
y_t = []
for t in range(seq_len):
x_t = x[:, t, :]
for layer in range(self.num_layers):
# psudo코드의 miniGRU 각 게이트별 연산 수행
z_t = torch.sigmoid(self.cells_z_t[layer](x_t if layer == 0 else h_t[layer-1]))
h_tilde = self.cells_h_tilde[layer](x_t if layer == 0 else h_t[layer-1])
#은닉 상태 업데이트 수행
h_t[layer] = (1 - z_t)*h_t[layer] + z_t*h_tilde
y_t.append(h_t[-1])
output = torch.stack(y_t, dim=1)
return output, h_tclass MiniLSTMSeq(nn.Module):
def __init__(self, input_size, hidden_size, num_layers=1):
super(MiniLSTMSeq, self).__init__()
# 주요 설계 파라미터를 먼저 선언
self.hidden_size = hidden_size
self.num_layers = num_layers
# miniLSTM는 게이트웨이가 간소화-> 3개
# 게이트웨이가 줄었으니 chunk로 분할하지 말고
# 그냥 게이트웨이별로 독립된 linear로 작성함
self.cells_f_t = nn.ModuleList([
nn.Linear(input_size if i == 0 else hidden_size, hidden_size)
for i in range(num_layers)
])
self.cells_i_t = nn.ModuleList([
nn.Linear(input_size if i == 0 else hidden_size, hidden_size)
for i in range(num_layers)
])
self.cells_h_tilde = nn.ModuleList([
nn.Linear(input_size if i == 0 else hidden_size, hidden_size)
for i in range(num_layers)
])
def forward(self, x, hidden=None):
bs, seq_len, _ = x.size()
# miniLSTM은 c_t 항목이 아에 없음
if hidden is None:
h_t = torch.zeros(self.num_layers, bs, self.hidden_size,
device=x.device, dtype=x.dtype)
else:
h_t, = hidden
y_t = []
for t in range(seq_len):
x_t = x[:, t, :]
for layer in range(self.num_layers):
# psudo코드의 miniGRU 각 게이트별 연산 수행
f_t = torch.sigmoid(self.cells_f_t[layer](x_t if layer == 0 else h_t[layer-1]))
i_t = torch.sigmoid(self.cells_i_t[layer](x_t if layer == 0 else h_t[layer-1]))
h_tilde = self.cells_h_tilde[layer](x_t if layer == 0 else h_t[layer-1])
f_prime_t = f_t / (f_t+i_t)
i_prime_t = i_t / (f_t+i_t)
# 은닉 상태 업데이트 수행
h_t[layer] = f_prime_t*h_t[layer] + i_prime_t*h_tilde
y_t.append(h_t[-1])
output = torch.stack(y_t, dim=1)
return output, h_t위 코드는 각각 miniGRU, miniLSTM의 psudo code를 바탕으로 구현한 항목이며
논문 : Were RNN All We Needed?에서 주요하게 언급하고 있는
parallel prefix scan 알고리즘은 적용되지 않은 상태이다
이제 해당 항목을 적용한 코드를 작성하고자 한다.
2) Parallel Mode miniGRU, miniLSTM 코드화
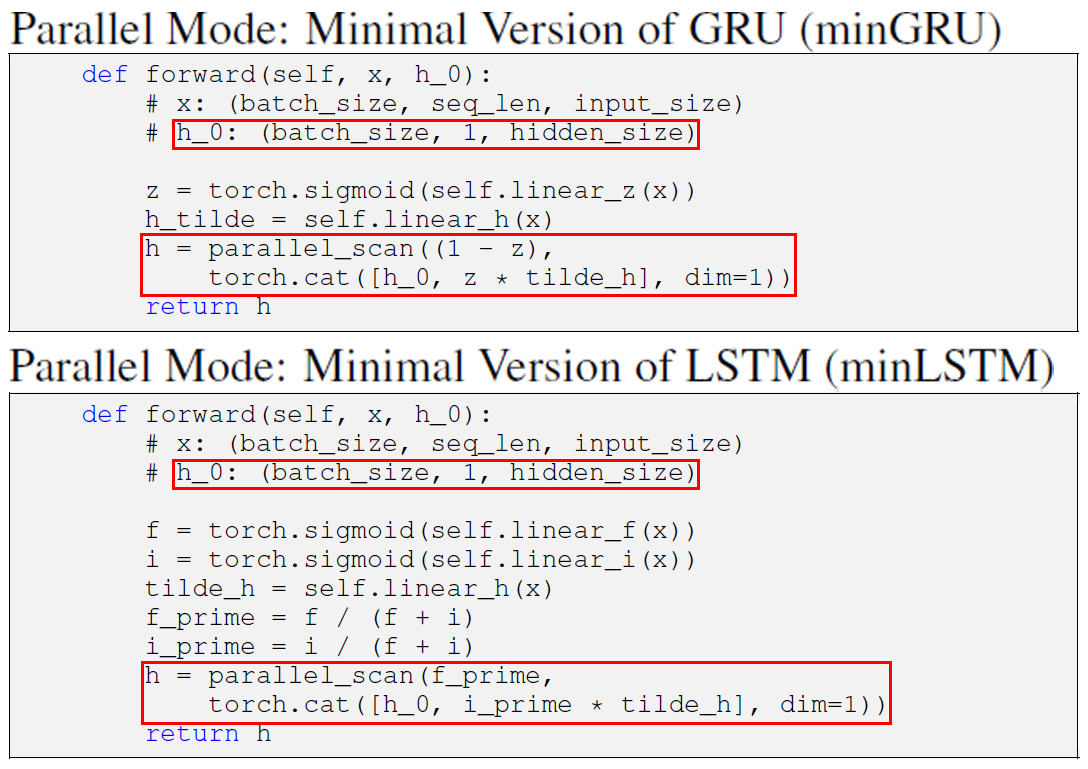
Parallel Mode버전의 miniGRU, miniLSTM를 설계할 때
가장 중요한 것은 의 차원이
(num_layers, Batch_size, hid_dim) (Batch_size, 1, hid_dim)
으로 변환시키는 과정을 수행하는 것과
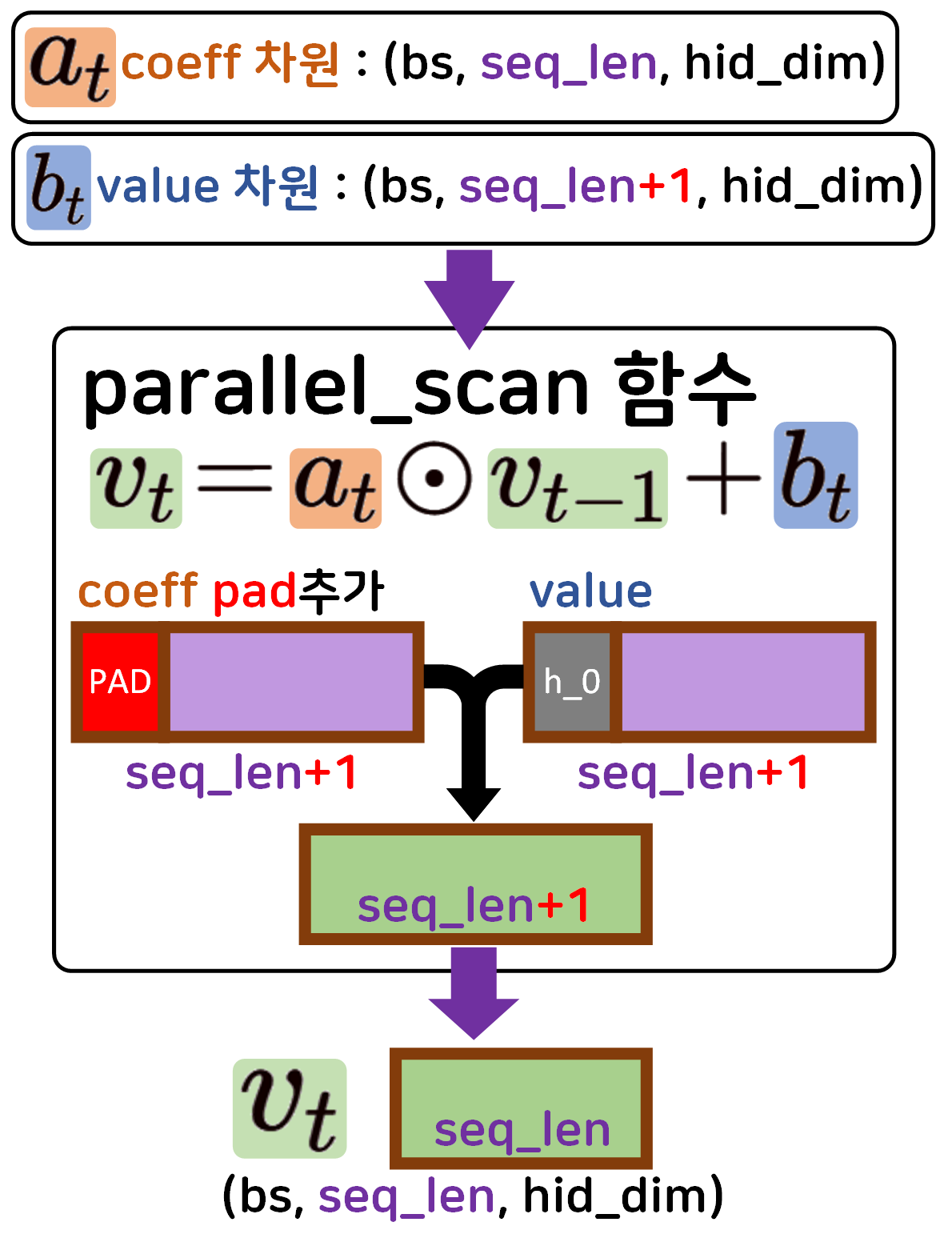
paraller_scan함수에 입력되는 두개의 인자값
coefficient(), value()이 각각 어떤 shape를 갖고
이것이 연산을 수행하면서 어떻게 변화하는지를 숙지해야한다.
이거 이해하는데 한참 걸렷다...
위 과정을 적용한 코드는 아래와 같다
참고로 Parallel Mode miniGRU, miniLSTM는 num_layers 옵션은 기본값 1로 고정하고 뺀다.
이 옵션까지 넣어서 코드작성이 안된다..
class MiniGRUPara(nn.Module):
def __init__(self, input_size, hidden_size):
super(MiniGRUPara, self).__init__()
# 주요 설계 파라미터를 먼저 선언
self.hidden_size = hidden_size
# miniGRU는 게이트웨이가 간소화-> 2개
self.cell_z = nn.Linear(input_size, hidden_size)
self.cell_h_tilde = nn.Linear(input_size, hidden_size)
def parallel_scan(self, coeff, value):
#v_t = a_t 곱 v_{t-1} 합 b_t 수식을 코드화
#여기서 a = coeff, b = value라 보면 된다.
# coeff의 차원은 (bs, seq_len, input_size) 이고
# value의 차원은(bs, seq_len+1, input_size) 이다.
#누적곱 연산 적용 후 pad 차원으로 (bs, seq_len+1, input_size)만들기
cum_coeff = F.pad(torch.cumprod(coeff, dim=1), (0, 0, 1, 0))
prefix = torch.cumsum(value * cum_coeff, dim=1) #누적합 연산 적용
# 이 연산을 통해서 prefix seq data가 출력됨
# 최종 연산 차원이(bs, seq_len+1, input_size)이니
# 슬라이싱을 통해서 (bs, seq_len, input_size)로 만들기
return prefix[:, 1:]
def forward(self, x, h_0=None):
bs, seq_len, _ = x.size()
#h_0은 원래 (num_layer, bs, seq_len, hid_dim)
# 차원이 되어야 하는데
# num_layer빠지고 seq_len은 첫 단어니까 1
if h_0 is None:
h_0 = torch.zeros(bs, 1, self.hidden_size,
device=x.device, dtype=x.dtype)
z = torch.sigmoid(self.cell_z(x))
h_tilde = self.cell_h_tilde(x)
coeff = 1-z
value = torch.cat([h_0, z * h_tilde], dim=1)
output = self.parallel_scan(coeff, value)
# 최종 output는 (bs, seq_len, input_size)
return outputclass MiniLSTMPara(nn.Module):
def __init__(self, input_size, hidden_size):
super(MiniLSTMPara, self).__init__()
# 주요 설계 파라미터를 먼저 선언
self.hidden_size = hidden_size
self.cell_f = nn.Linear(input_size, hidden_size)
self.cell_i = nn.Linear(input_size, hidden_size)
self.cell_h_tilde = nn.Linear(input_size, hidden_size)
def parallel_scan(self, coeff, value):
#v_t = a_t 곱 v_{t-1} 합 b_t 수식을 코드화
cum_coeff = F.pad(torch.cumprod(coeff, dim=1), (0, 0, 1, 0))
prefix = torch.cumsum(value * cum_coeff, dim=1) #누적합 연산 적용
# 슬라이싱을 통해서 (bs, seq_len, input_size)로 만들기
return prefix[:, 1:]
def forward(self, x, h_0=None):
bs, seq_len, _ = x.size()
if h_0 is None:
h_0 = torch.zeros(bs, 1, self.hidden_size,
device=x.device, dtype=x.dtype)
f = torch.sigmoid(self.cell_f(x))
i = torch.sigmoid(self.cell_i(x))
h_tilde = self.cell_h_tilde(x)
f_prime = f / (f+i)
i_prime = i / (f+i)
coeff = f_prime
value = torch.cat([h_0, i_prime * h_tilde], dim=1)
output = self.parallel_scan(coeff, value)
return output3) parallel prefix scan 수치적 안정성 개선
위 2) 과정을 수행하면서 적용한 parallel_scan 함수는
cumprod(누적곱) 연산을 사용하여 prefix seq data를 생성해 내는데
이 cumprod(누적곱) 연산은 수치적으로 불안정성이 존재하며, 쉽게 설명하면 오버플로우/언더플로우가 쉬이 발생하기 쉬운 구조라 보면 된다.
따라서 코드개선이 이뤄지며
입력 데이터 및 연산과정을 모두 로그 공간에서 수행한 뒤
마지막에 지수변환으로 원래 공간으로 변환하는 함수를 사용한다.

따라서 해당 함수만 따로 구현한다면 아래의 코드가 된다
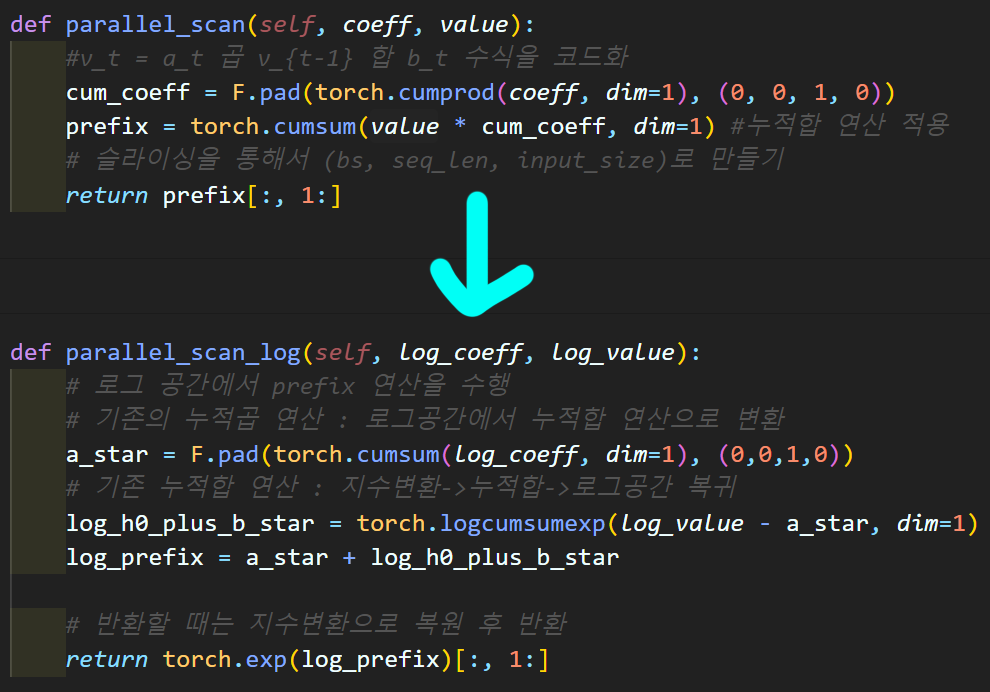
4)
parallel_scan_log를 적용한 Parallel Mode miniGRU
수치적 안정성이 적용된 parallel_scan_log 함수를 설계했으니
이를 Parallel Mode miniGRU에 적용하는 과정에 대해 기술하고자 한다.
Sequential Mode miniGRU에도 parallel_scan_log함수를 적용할 수는 있지만
어차피 최종적으로 사용되는건 Parallel Mode miniGRU이기에 해당 항목만 다루고자 한다.

위 그림처럼 coefficient(), value()에 해당하는 인자값들이 log_space로 전이 parallel_scan_log 함수의 인자값으로 사용 과정을 거쳐야 하기에
각각의 항목들이 log_space로 변환되는 수식을 숙지해야 한다.
설명이 길긴 했지만 , 항목에 대한 psudo code는 아래의 사진을 참조하면 된다.


이를 코드화 한다면 아래와 같아진다.
class MiniGRUParaLog(nn.Module):
def __init__(self, input_size, hidden_size):
super(MiniGRUParaLog, self).__init__()
# 주요 설계 파라미터를 먼저 선언
self.hidden_size = hidden_size
# miniGRU는 게이트웨이가 간소화-> 2개
self.cell_z = nn.Linear(input_size, hidden_size)
# 로그공간으로 인해 h_tilde가 아닌 h가 그대로 쓰임
self.cell_h = nn.Linear(input_size, hidden_size)
def parallel_scan_log(self, log_coeff, log_value):
# 로그 공간에서 prefix 연산을 수행
# 기존의 누적곱 연산 : 로그공간에서 누적합 연산으로 변환
a_star = F.pad(torch.cumsum(log_coeff, dim=1), (0,0,1,0))
# 기존 누적합 연산 : 지수변환->누적합->로그공간 복귀
log_h0_plus_b_star = torch.logcumsumexp(log_value - a_star, dim=1)
log_prefix = a_star + log_h0_plus_b_star
# 반환할 때는 지수변환으로 복원 후 반환
return torch.exp(log_prefix)[:, 1:]
def g(self, x): # h_tilde의 변환에 사용되는 함수
return torch.where(x >= 0, x+0.5, torch.sigmoid(x))
def log_g(self, x): # h_tilde의 log공간 변환에 사용되는 함수
return torch.where(x >= 0, (F.relu(x)+0.5).log(), -F.softplus(-x))
def forward(self, x, h_0=None):
bs, seq_len, _ = x.size()
if h_0 is None:
h_0 = torch.zeros(bs, 1, self.hidden_size,
device=x.device, dtype=x.dtype)
k = self.cell_z(x)
log_coeff = -F.softplus(k)
log_z = -F.softplus(-k) #value의 첫번째 인자
log_tilde_h = self.log_g(self.cell_h(x)) # value의 두번째 인자.
log_h_0 = self.log_g(h_0)
log_value = torch.cat([log_h_0, log_z + log_tilde_h], dim=1)
output = self.parallel_scan_log(log_coeff, log_value)
# 최종 output는 (bs, seq_len, input_size)
return output5)
parallel_scan_log를 적용한 Parallel Mode miniLSTM

miniLSTM도 parallel_scan_log로 인해 인자값을 사전에 log_space로 보내야 하니 그 과정을 수식으로 표현하면 위와 같아진다.
문제는 위 수식을 psudo code로 표현한것이 살짝 다르다는 것이다.

인자값 정의가 수식이랑 psudo_code가 다른게 좀 걸리지만
코드화는 psudo_code를 기반으로 진행하겠다.
class MiniLSTMParaLog(nn.Module):
def __init__(self, input_size, hidden_size):
super(MiniLSTMParaLog, self).__init__()
# 주요 설계 파라미터를 먼저 선언
self.hidden_size = hidden_size
self.cell_f = nn.Linear(input_size, hidden_size)
self.cell_i = nn.Linear(input_size, hidden_size)
self.cell_h = nn.Linear(input_size, hidden_size)
def parallel_scan_log(self, log_coeff, log_value):
# 로그 공간에서 prefix 연산을 수행
# 기존의 누적곱 연산 : 로그공간에서 누적합 연산으로 변환
a_star = F.pad(torch.cumsum(log_coeff, dim=1), (0,0,1,0))
# 기존 누적합 연산 : 지수변환->누적합->로그공간 복귀
log_h0_plus_b_star = torch.logcumsumexp(log_value - a_star, dim=1)
log_prefix = a_star + log_h0_plus_b_star
# 반환할 때는 지수변환으로 복원 후 반환
return torch.exp(log_prefix)[:, 1:]
def g(self, x): # h_tilde의 변환에 사용되는 함수
return torch.where(x >= 0, x+0.5, torch.sigmoid(x))
def log_g(self, x): # h_tilde의 log공간 변환에 사용되는 함수
return torch.where(x >= 0, (F.relu(x)+0.5).log(), -F.softplus(-x))
def forward(self, x, h_0=None):
bs, seq_len, _ = x.size()
if h_0 is None:
h_0 = torch.zeros(bs, 1, self.hidden_size,
device=x.device, dtype=x.dtype)
diff = F.softplus(-self.cell_f(x)) - F.softplus(-self.cell_i(x))
log_f_prime = -F.softplus(diff) #이게 log_coeff
log_i_prime = -F.softplus(-diff)
log_tilde_h = self.log_g(self.cell_h(x))
log_h_0 = self.log_g(h_0)
log_value = torch.cat([log_h_0, log_i_prime + log_tilde_h], dim=1)
output = self.parallel_scan_log(log_f_prime, log_value)
return output2.1 코드 모듈화
miniLSTM, miniGRU는 참 코드 만들기도 복잡해서 모듈화 해서 사용하는게 편하다...
모듈화한 코드는 https://github.com/tbvjvsladla/MiniRNN/blob/main/MiniRNN.py 에 업로드하였다.
사용 방법은 해당 코드를 다운로드 받은 뒤
다른 메인 파이썬 혹은 ipynb파일에서
from MiniRNN import MiniGRU, MiniLSTMimport torch
# 예제 입력 하이퍼 파라미터 선언
input_size = 25
hidden_size = 50
seq_len = 5
batch_size = 128
# 예제 입력 텐서 선언
inputs = torch.randn(batch_size, seq_len, input_size)mini_LSTM = MiniLSTM(input_size, hidden_size)
mini_GRU = MiniGRU(input_size, hidden_size)
output_1 = mini_LSTM(inputs)
output_2 = mini_GRU(inputs)
print(output_1.shape, output_2.shape) # 출력 차원 확인torch.Size([128, 5, 50]) torch.Size([128, 5, 50])위와 같은 방식으로 사용하면 된다.
3. 문장 분류 실습
이전 포스트 2. NLP-LSTM, GRU (2) : 텍스트 분류기
의 실습자료인 span_SNS.csv를 그대로 사용하며
데이터 전처리 텍스트 전처리
과정은 생략한다.
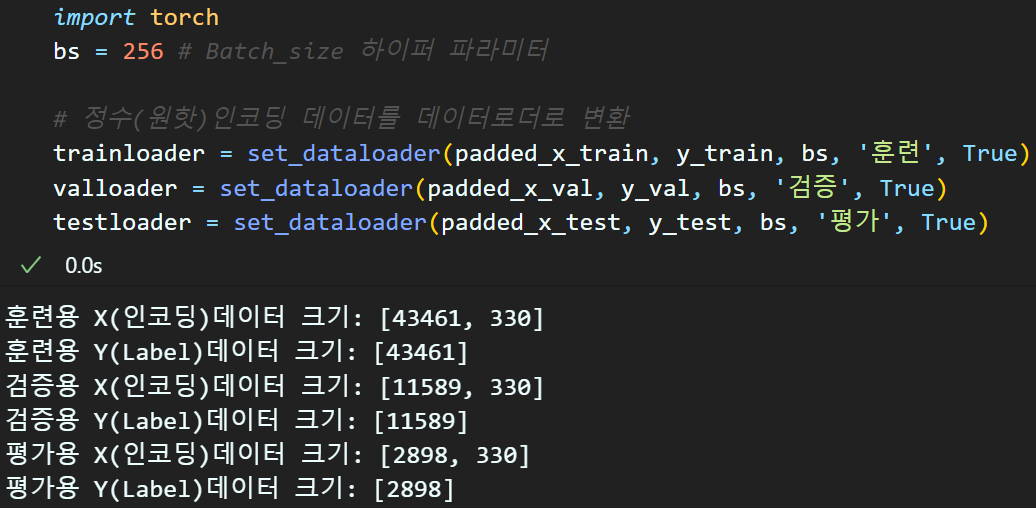
아무튼 모델에 입력되는 데이터로더의 구성은 위와 같게 처리했다.
임베딩 레이어는 FastText방법론을 사용했으며
2. NLP - CNN기반 문장 classification (2-1)에 코드가 있으니 이를 참조 바란다
아무튼 학습 코드는 아래와 같다.
주요 하이퍼 파라미터 정의
# 주요 하이퍼 파라미터 정의
VOCAB_SIZE = len(word_to_idx)
CONTEXT_LEN = context_length
EMB_DIM = FT_model.wv.vector_size
NUM_CLASS = len(set(raw_y_label))
HIDE_DIM = 1400
print(f'''주요 하이퍼 파라미터 : {VOCAB_SIZE},
{CONTEXT_LEN}, {EMB_DIM}, {NUM_CLASS}, {HIDE_DIM}''')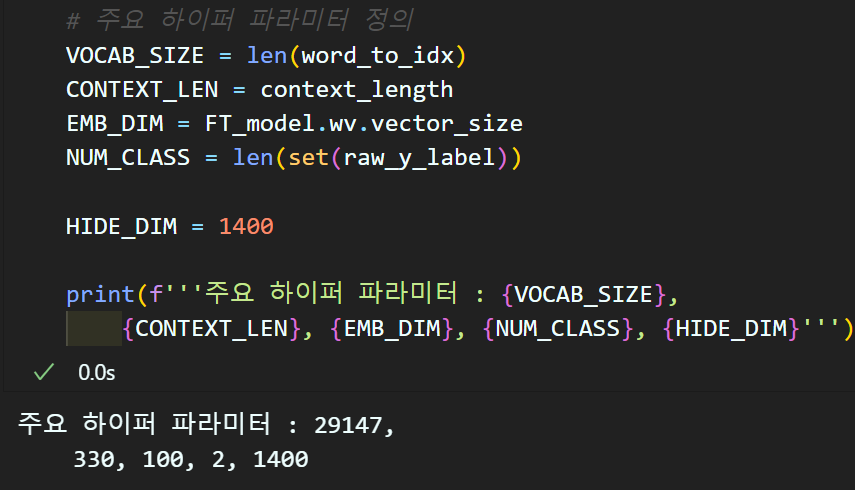
모델 정의
import torch.nn as nnclass WereLSTM(nn.Module):
def __init__(self, vocab_size, embed_dim, num_classes,
hid_dim, emb_matirx=None):
super(WereLSTM, self).__init__()
self.embed = nn.Embedding(vocab_size, embed_dim)
if emb_matirx is not None:
# 사전 훈련된 임베딩 매트릭스를 붙여넣음
self.embed.weight = nn.Parameter(
torch.tensor(emb_matirx, dtype=torch.float32))
# 붙여넣은 Pretrained 임베드 레이어만 Freeze하고 싶을때는 False
self.embed.weight.requires_grad = True
self.mini_lstm = MiniLSTM(input_size=embed_dim,
hidden_size=hid_dim)
self.classifier = nn.Sequential(
nn.Linear(hid_dim, num_classes),
)
def forward(self, x):
emb = self.embed(x)
lstm_out = self.mini_lstm(emb)
# lstm_out의 마지막 시퀀스 출력 사용
out = lstm_out[:, -1, :]
out = self.classifier(out)
return outclass WereGRU(nn.Module):
def __init__(self, vocab_size, embed_dim, num_classes,
hid_dim, emb_matirx=None):
super(WereGRU, self).__init__()
self.embed = nn.Embedding(vocab_size, embed_dim)
if emb_matirx is not None:
# 사전 훈련된 임베딩 매트릭스를 붙여넣음
self.embed.weight = nn.Parameter(
torch.tensor(emb_matirx, dtype=torch.float32))
# 붙여넣은 Pretrained 임베드 레이어만 Freeze하고 싶을때는 False
self.embed.weight.requires_grad = True
self.mini_gru = MiniGRU(input_size=embed_dim,
hidden_size=hid_dim)
self.classifier = nn.Sequential(
nn.Linear(hid_dim, num_classes),
)
def forward(self, x):
emb = self.embed(x)
gru_out = self.mini_gru(emb)
# gru_out의 마지막 시퀀스 출력 사용
out = gru_out[:, -1, :]
out = self.classifier(out)
return out# 학습 실험 조건을 구분하기 위한 키
model_key = ['miniLSTM', 'miniGRU']
cod_key = ['랜덤초기화', '사전훈련']
metrics_key = ['Loss', '정확도']
key_list = [f"{mk}_{ck}" for mk in model_key for ck in cod_key]LSTM_model_raninit = WereLSTM(VOCAB_SIZE, EMB_DIM,
NUM_CLASS, HIDE_DIM)
LSTM_model_pre_emb = WereLSTM(VOCAB_SIZE, EMB_DIM,
NUM_CLASS, HIDE_DIM, my_FT_embedding)
GRU_model_raninit = WereGRU(VOCAB_SIZE, EMB_DIM,
NUM_CLASS, HIDE_DIM)
GRU_model_pre_emb = WereGRU(VOCAB_SIZE, EMB_DIM,
NUM_CLASS, HIDE_DIM, my_FT_embedding)# GPU사용 가능 유/무 확인
device = torch.device("cuda" if torch.cuda.is_available() else 'cpu')
models = {} # 딕셔너리
models[key_list[0]] = LSTM_model_raninit.to(device)
models[key_list[1]] = LSTM_model_pre_emb.to(device)
models[key_list[2]] = GRU_model_raninit.to(device)
models[key_list[3]] = GRU_model_pre_emb.to(device)학습 하이퍼 파라미터 정의
import torch.optim as optim
# 로스함수 및 옵티마이저 설계
criterion = nn.CrossEntropyLoss()
LR = 0.001 # 러닝레이트는 통일
optimizers = {}
optimizers[key_list[0]] = optim.Adam(LSTM_model_raninit.parameters(), lr=LR)
optimizers[key_list[1]] = optim.Adam(LSTM_model_pre_emb.parameters(), lr=LR)
optimizers[key_list[2]] = optim.Adam(GRU_model_raninit.parameters(), lr=LR)
optimizers[key_list[3]] = optim.Adam(GRU_model_pre_emb.parameters(), lr=LR)# 사전에 모듈화 한 학습/검증용 라이브러리 import
from C_ModelTrainer import ModelTrainer
num_epoch = 8 #총 훈련/검증 epoch값
ES = 2 # 디스플레이용 에포크 스텝
# BC_mode = True(이진), False(다중)
# aux = 보조분류기 유/무
# wandb = 완디비에 연결 안하면 None
# iter = 훈련시 iteration의 acc및 loss 정보 추출
trainer = ModelTrainer(epoch_step=ES, device=device,
BC_mode=False, aux=False, iter=False)# 학습/검증 정보 저장
history = {key: {metric: []
for metric in metrics_key}
for key in key_list}학습 시작
#실험조건 : 모델 + 임베딩레이어 pretrain 유/무
for key in key_list:
# 모델 훈련/검증 코드
for epoch in range(num_epoch):
# 훈련모드의 손실&성과 지표
train_loss, train_acc = trainer.model_train(
models[key], trainloader,
criterion, optimizers[key], epoch)
# 검증모드의 손실&성과 지표
val_loss, val_acc = trainer.model_evaluate(
models[key], valloader,
criterion, epoch)
# 손실 및 성과 지표를 history에 저장
history[key]['Loss'].append((train_loss, val_loss))
history[key]['정확도'].append((train_acc, val_acc))
# Epoch_step(ES)일 때마다 print수행
if (epoch+1) % ES == 0 or epoch == 0:
if epoch == 0:
print(f"현재 훈련중인 조건: [{[key]}]")
print(f"epoch {epoch+1:03d}," + "\t" +
f"훈련 [Loss: {train_loss:.3f}, " +
f"Acc: {train_acc*100:.2f}%]")
print(f"epoch {epoch+1:03d}," + "\t" +
f"검증 [Loss: {val_loss:.3f}, " +
f"Acc: {val_acc*100:.2f}%]")
print(f"\n----조건[{[key]}] 훈련 종료----\n")학습 결과를 확인한다면
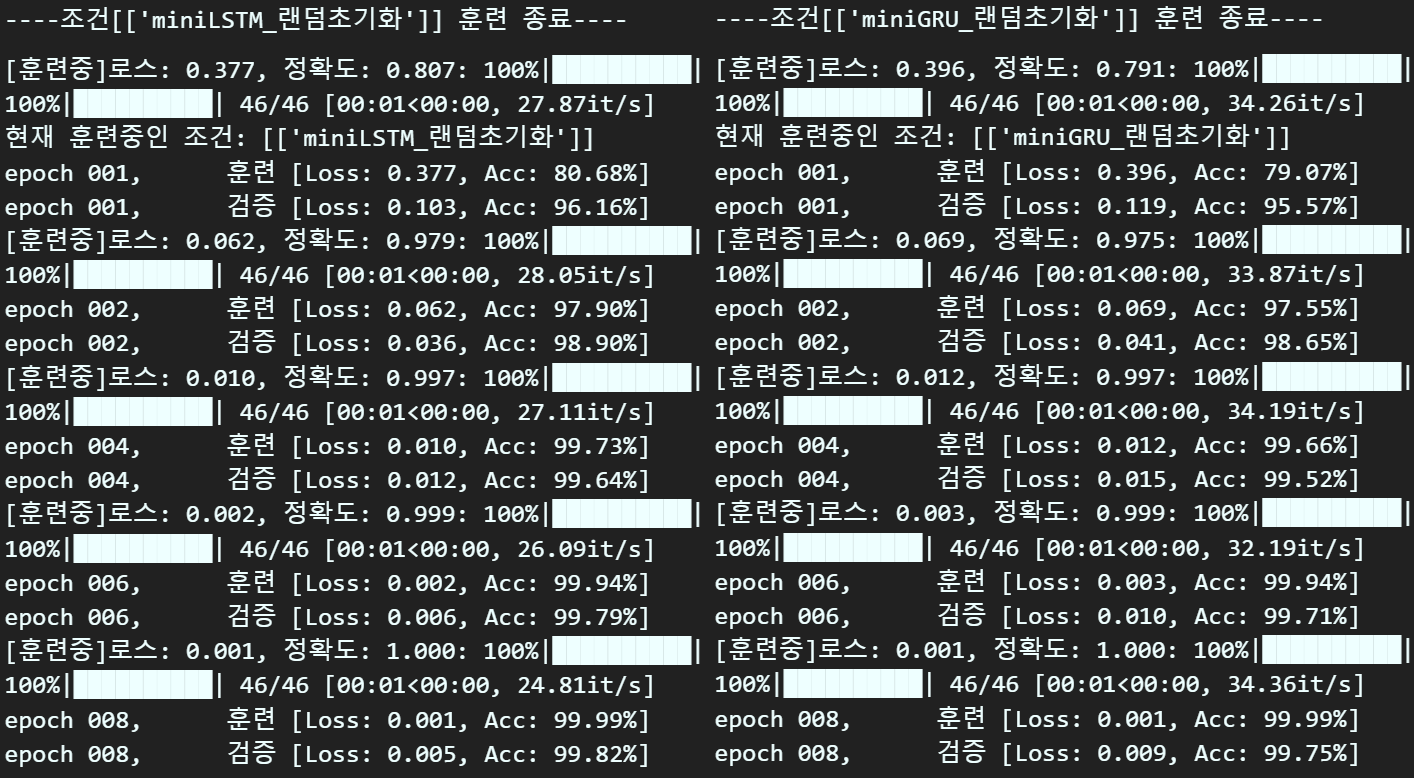
성능 잘나온다
중간에 Loss가 NaN이 발생해서 코드 오류가 나서 안정성이 덜 확보됬나 하고 다시 검증해 보니
기호를 + 써야 할 곳에 *를 썻다...
https://github.com/MOVzeroOne/modernized_rnn/tree/main
코드 참조는 위 깃허브의 miniGRU, miniLSTM랑 교차검증을 수행했다.
논문에서는 학습 할때는 parallel mode로하고
검증할 때는 sequence mode로 하라고 써 있는데
그냥 parallel mode원툴로 돌려도 무방할 듯 하다.
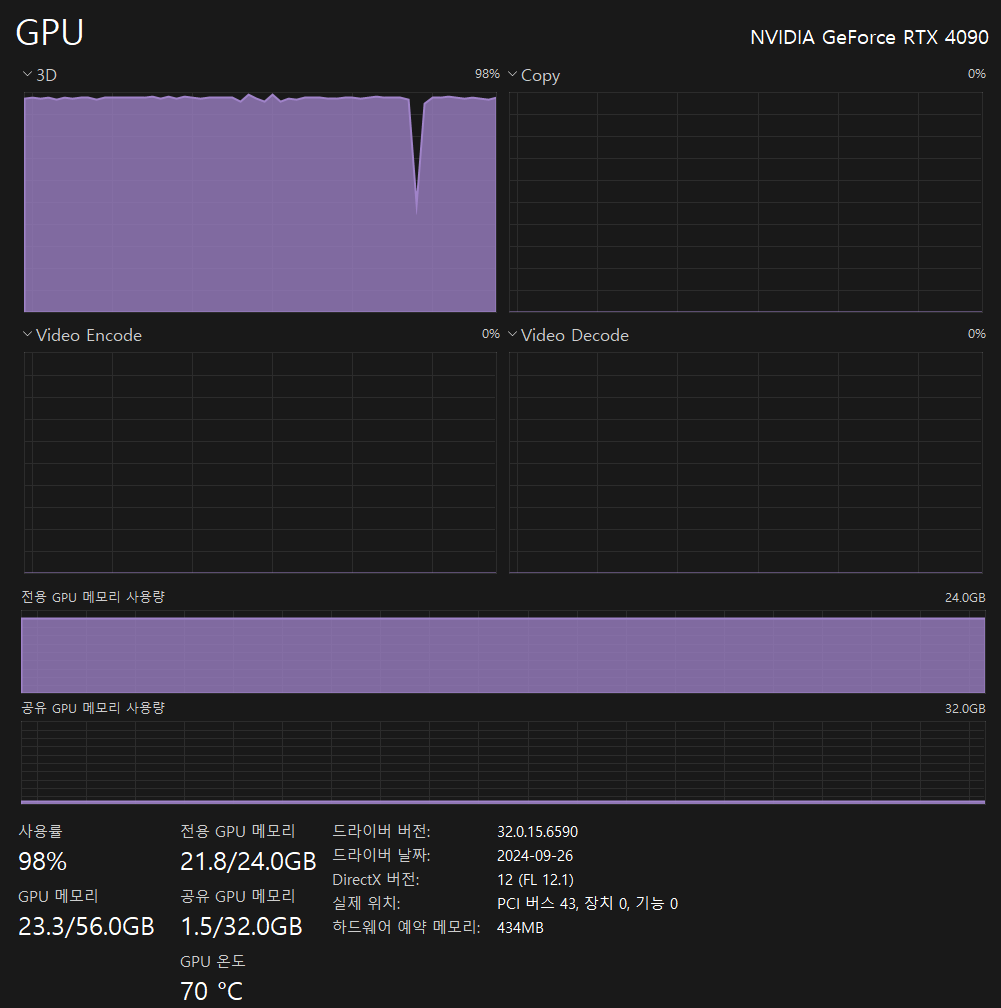
단, GPU자원은 신나게 빨아먹는걸 보아하니 꽤 무거운 모델인것은 감안하고 구동해야 한다.
논문이 올해 출간한 최신 논문이어서 자료도 별로 없고
어려운 개념도 많아서 포스팅 하는데 시간이 오래걸리긴 했다.
그래도 수식 정리 + psudo code 학습 등
재미있는 시간이었다.