확산확률모델

Diffusion Probabilistic Model

---

확산 현상

• 물질(픽셀값)이 섞이고 번져가다가 마지막에는 균일한 농도(노이즈)가 되는 현상임.

확산현상을 시간에 따라 확률적 모델리으로, 마르코프 체인(미래는 과거가 아닌 현재에만 의존함)

1. DPM의 구조

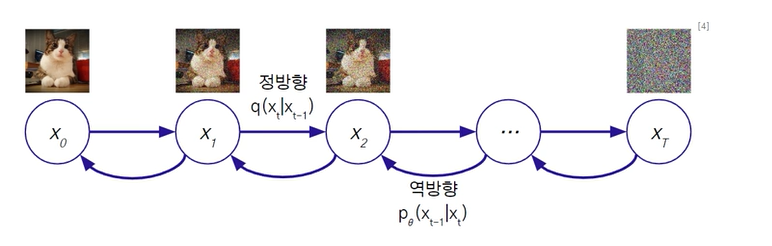
• 정방향확산 : 데이터 -> 노이즈 (고정)
• 역방향확산 : 데이터 <- 노이즈 (학습)

완전 노이즈는 정규분포를 따르게 됨. ($X_T$)
완전 노이즈로부터 역방향으로 물감을 빼주는 과정

2. 정방향 확산

• 이미지의 파괴 과정으로 T=1000 시점동안 노이즈를 점진적으로 계속 주입함. (정규분포를 따르도록)
  시간에 따라 노이즈의 파라미터 $\beta$의 값을 0.0001 -> 0.02로 증가하도록 정함.

3. 역방향 확산

• 이미지의 생성 과정 = 노이즈를 제거하는 과정으로 계산이 불가함. (모든 데이터를 고려해야함)
  여기서 만약 $\beta$ (노이즈) 작을때 정규분포로 근사 가능. (열 확산 연구로 도출되었음)

• 다시말해, 정규분포 근사를 통해서, 매 시점마다 정규분포 형태를 가지며 이는 정방향 확산과 유사함.

4. 손실함수

• VAE와 유사하게 log 가능도의 하한을 최대화 하는 것임.

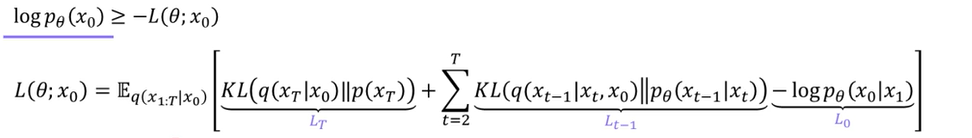
• 정방향 확산이 이루어지는 가 ?

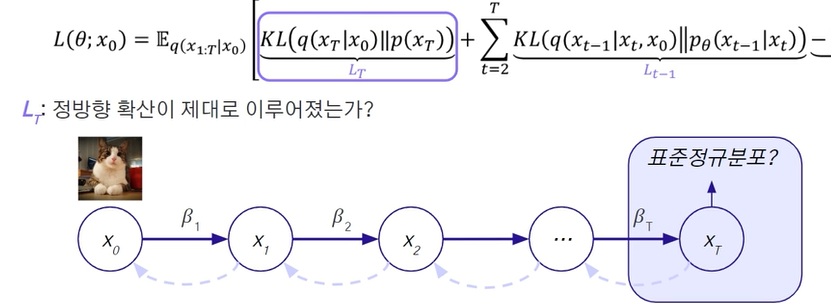
위 수식에서 처럼 표준 정규분포를 따르기에 쿨백-라이블러의 계산이 이루어짐.

• 역방향 확산, 재구성이 잘 되는 것인가 ?
  

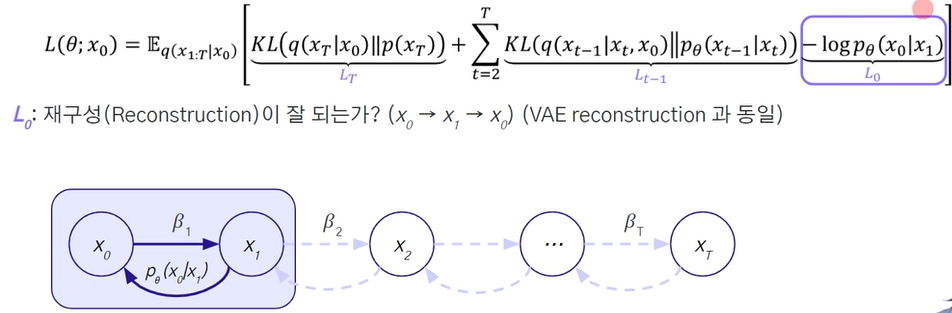
노이즈가 있는 곳에서 다시 원본으로 돌아올 수 있는 지를 봄.

• t시점의 노이즈를 모델이 제대로 제거하였는 가?
  

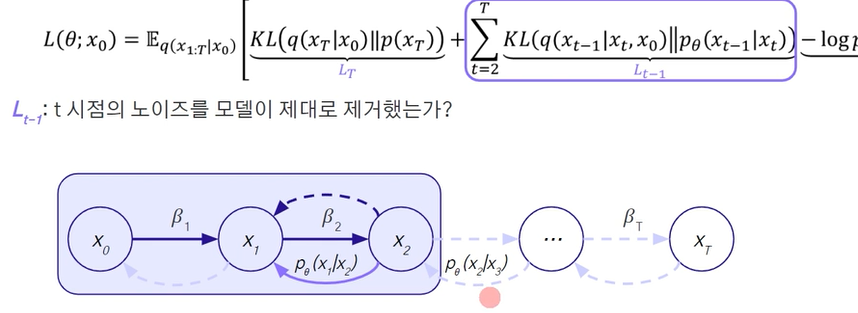
수식으로 나타나게 되면, 2개의 정규분포에서의 계산은 분산은 동일하므로

다음과 같이 Mean의 값의 MSE로 표현되게 됨.

5. VAE와 차이점

• 잠재변수의 차원이 모두 데이터의 차원과 동일하며, 여러 단계의 잠재변수(노이즈를 더하는 step에 따라 점진적($\beta$의 값)으로 달라짐)를 가짐.

• 디코더를 모든 시점에서 공유되며, 인코더는 학습되지 않음

---

디노이징 확산확률모델 - DDPM

손실함수

• 데이터를 예측하는 것보다 노이즈를 예측할 때, 더 좋은 성능을 보이는 점을 이용함.

• 손실함수를 간단한 형태로 정리함.
  

• 기존에는 특정 시점의 평균을 구하고, 쿨백-라이블러를 이용하였음.
  디노이징의 경우, $L_T$; 첫번째 항을 0이 되도록 $\beta_t$를 설정하였음.
  기존에는 다 더해서 표준정규분포가 되도록 하였지만, 랜덤하게 더하여도 표준정규분포가 되도록 하였음.

• $L_{t-1}$에서 상수 제거함. 분산으로 나누는 것을 서로다른 가중치를 주는 것으로 대체하였음.

DDPM의 한계점

• 느린 생성 과정
• 조건부 생성 불가, (품질 precision, 다양성 recall)

생성 모델의 3요소

• 높은 품질 ---- GAN, DPM
• 빠른 샘플 --- GAN, VAE
• 다양한 샘플 --- VAE, DPM

DDIM

• T = 1000보다 적은 시점을 거쳐서 데이터를 생성할 수 있을까 ?
  마르코프 체인 가정을 없앴음. -> 즉 1000번 다 되어야 알 수 있던 한계를 제거하기 위함임.

기존

샘플링 과정에서 마르코프 체인은 $x_{t-1}$의 상태는 노이즈가 덜 낀 상태임.

• 따라서, 마르코프 체인을 가정하지 않고서, 학습딘 모델의 일부 시점만 거쳐 데이터 생성하여 생성 속도를 개선하려고 함.

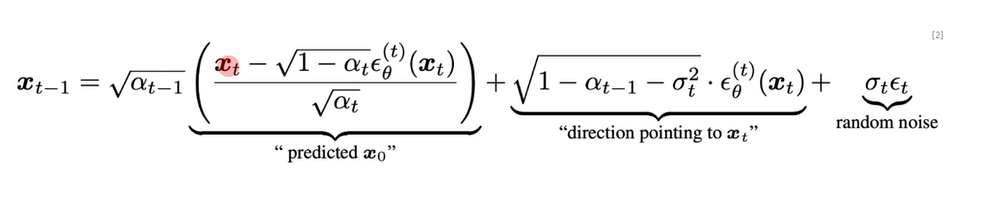
위의 수식으로 정리가 가능하며, x0는 첫번째항과 동치라 볼 수 있으며,
두번째 항은 x0에다가 노이즈를 추가한 것이다.

---

DDG

• 기존 DDPM의 핵심은 노이즈가 작을때는 정규분포로 근사 가능하다는 것이었는데 만약 노이즈가 크다면 시점이 0에 가까울수록 디노이징 분포가 정규분포보다 복잡해지게 되며
  이를 해결하기 위해 적은 시점을 사용하기 위하여 조건부 GAN을 활용함.

---

잠재확산 모델 (LDPM, LDM)

• 기존의 고해상도 이미지 생성 분야에서의 문제는 많은 양의 계산 자원을 필요하게 됨.

1. 픽셀공간에서 잠재공간

• 기존의 확산 모델들은 고차원 이미지 공간에서 연산을 반복함.
• 이미지의 정보를 유지한채로, 차원을 축소한다면 계산 복잡도를 감소 시킬 수 있음.

인지적 압축

• 과도한 세부 사항을 제거하여, 핵심적인 특징을 잠재표현으로 요약

의미적 압축

• 데이터의 의미적, 구조적 특징을 학습

1. 방법

• 입력 이미지를 인코더를 통해 축소시키고, 모델을 학습한 뒤 다시 디코더로 재건함.
• 적대적 오토 인코더 활용함.

Stable Diffusion - 과도한 세부 사항들을 제거한 것.