국내 박스오피스 영화 EDA & ML

Theo Kim·2023년 1월 1일

데이터 준비

import pandas as pd
import numpy as np

df = pd.read_excel('all_movies.xlsx', index_col=0)

인덱스 재설정

df.reset_index(drop=True, inplace=True)
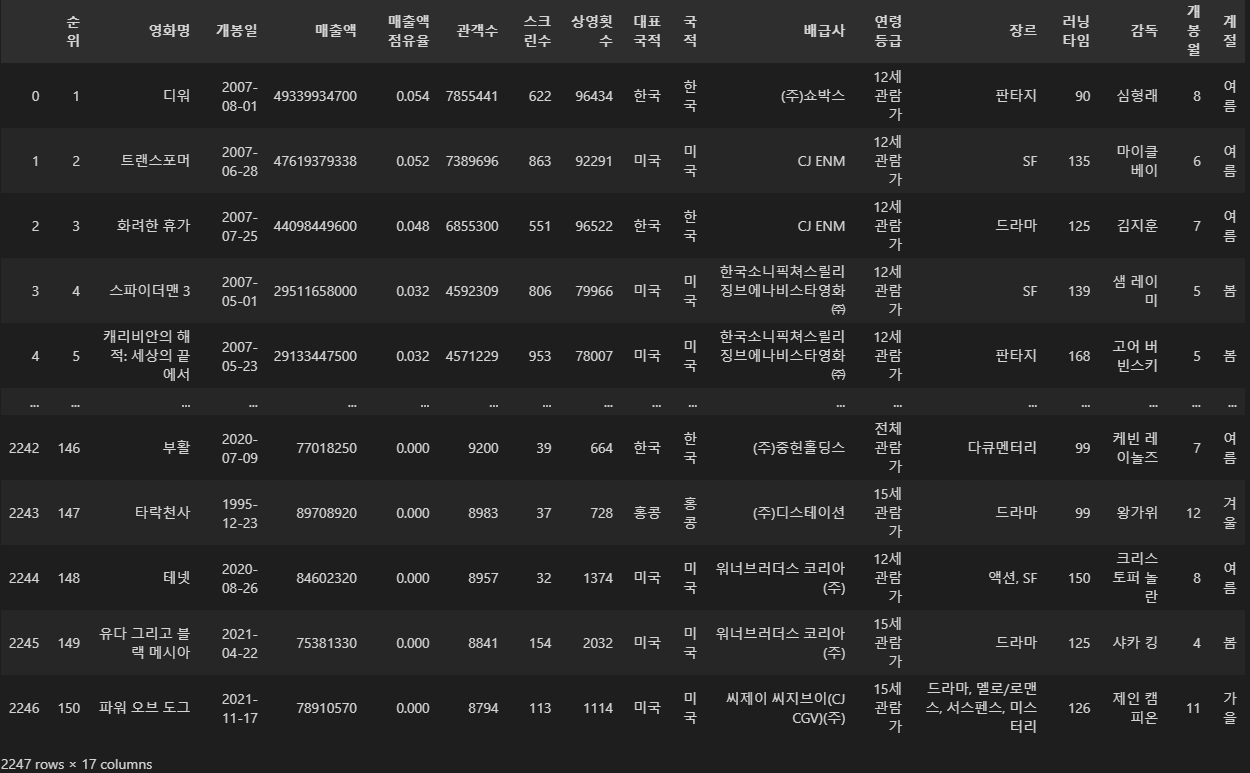
df
df.columns

중복 영화명에서 첫 영화 빼고 제거

df = df.drop_duplicates(['영화명'], keep='first')
df

영화 장르 첫 번째 빼고 다 제거

genre = []

for i in df['장르']:
  genre.append(i.split(',')[0])
df['장르'] = genre
df['장르'].unique()

러닝타임 0분 조회

df[df['러닝타임'] == 0]
# 0에서 17로 수정

df.loc[1033, '러닝타임'] = 17
df[df['러닝타임'] == 0]

연령등급 확인

df['연령등급'].unique()

Label Encode

from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()

# 대표국적
df['대표국적_le'] = le.fit_transform(df['대표국적'])

# 연령등급
df['연령등급_le'] = le.fit_transform(df['연령등급'])

# 장르
df['장르_le'] = le.fit_transform(df['장르'])

# 계절
df['계절_le'] = le.fit_transform(df['계절'])
df_ml = df[['순위', '매출액', '매출액 점유율', '관객수', '스크린수', '상영횟수', '러닝타임', '개봉월', '대표국적_le', '연령등급_le', '장르_le', '계절_le']]
df_ml

float로 변환

df_ml = df_ml.astype('float')
df_ml

EDA

매출액에 대한 히스토그램

import plotly.express as px

fig = px.histogram(df_ml, x='매출액')
fig.show()

수치 확인

df_ml.describe()

분포 확인

import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib import rc

plt.rcParams['axes.unicode_minus'] = False  # 마이너스 부호 때문에 한글이 깨질 수 있어 주는 설정

rc('font', family='NanumGothic')
# %matplotlib inline
get_ipython().run_line_magic('matplotlib', 'inline')
sns.set_style('darkgrid')
sns.set(rc={'figure.figsize': (20, 8)})
plt.rcParams['font.family'] = 'Malgun Gothic'

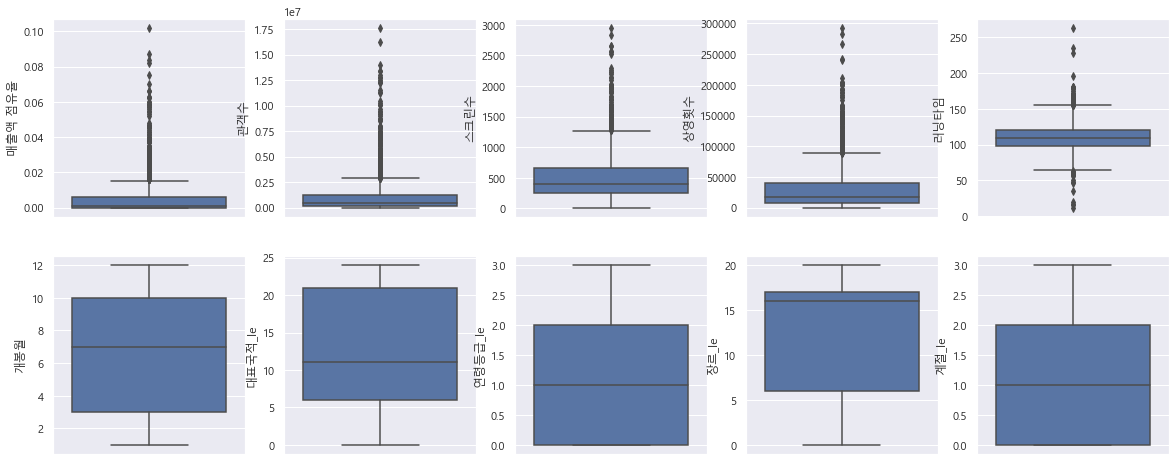
fig, ax = plt.subplots(ncols=5, nrows=2)
sns.boxplot(y='매출액 점유율', data=df_ml, ax=ax[0, 0])
sns.boxplot(y='관객수', data=df_ml, ax=ax[0, 1])
sns.boxplot(y='스크린수', data=df_ml, ax=ax[0, 2])
sns.boxplot(y='상영횟수', data=df_ml, ax=ax[0, 3])
sns.boxplot(y='러닝타임', data=df_ml, ax=ax[0, 4])
sns.boxplot(y='개봉월', data=df_ml, ax=ax[1, 0])
sns.boxplot(y='대표국적_le', data=df_ml, ax=ax[1, 1])
sns.boxplot(y='연령등급_le', data=df_ml, ax=ax[1, 2])
sns.boxplot(y='장르_le', data=df_ml, ax=ax[1, 3])
sns.boxplot(y='계절_le', data=df_ml, ax=ax[1, 4])

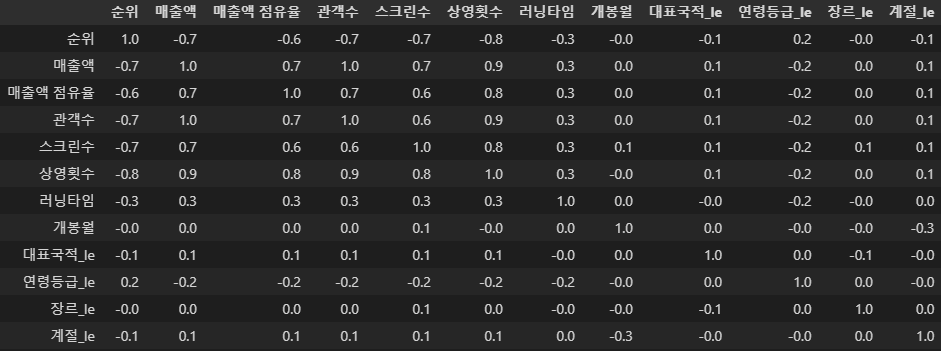
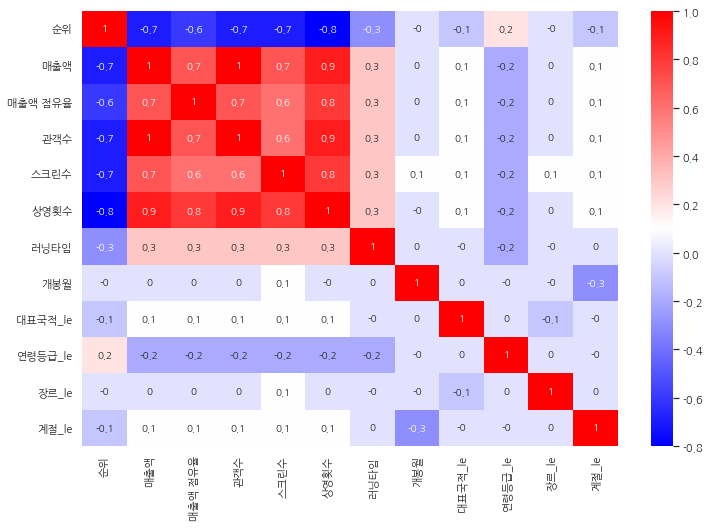
상관관계

import seaborn as sns

corr_mat = df_ml.corr().round(1)
corr_mat

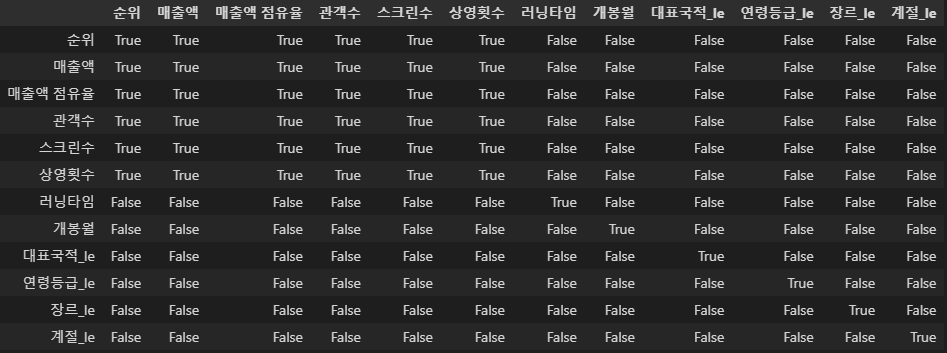
abs(corr_mat) > 0.5

plt.figure(figsize=(12, 8))
sns.heatmap(data=corr_mat, annot=True, cmap='bwr');

sns.pairplot(data=df_ml);

sns.set_style('darkgrid')
sns.set(rc={'figure.figsize': (20, 8)})
plt.rcParams['font.family'] = 'Malgun Gothic'

fig, ax = plt.subplots(ncols=5, nrows=2)
sns.regplot(x='매출액 점유율', y='매출액', data=df_ml, ax=ax[0, 0])
sns.regplot(x='관객수', y='매출액', data=df_ml, ax=ax[0, 1])
sns.regplot(x='스크린수', y='매출액', data=df_ml, ax=ax[0, 2])
sns.regplot(x='상영횟수', y='매출액', data=df_ml, ax=ax[0, 3])
sns.regplot(x='러닝타임', y='매출액', data=df_ml, ax=ax[0, 4])
sns.regplot(x='개봉월', y='매출액', data=df_ml, ax=ax[1, 0])
sns.regplot(x='대표국적_le', y='매출액', data=df_ml, ax=ax[1, 1])
sns.regplot(x='연령등급_le', y='매출액', data=df_ml, ax=ax[1, 2])
sns.regplot(x='장르_le', y='매출액', data=df_ml, ax=ax[1, 3])
sns.regplot(x='계절_le', y='매출액', data=df_ml, ax=ax[1, 4])

OLS 분석

from statsmodels.formula.api import ols
df_ml.columns

# ols를 위해 컬럼명 공백 제거
df_ml_ols = df_ml.rename(columns={'매출액 점유율':'매출액_점유율'})
ols('매출액 ~ 매출액_점유율 + 관객수 + 스크린수 + 상영횟수 + 러닝타임 + 개봉월 + 대표국적_le + 연령등급_le + 장르_le + 계절_le', data=df_ml_ols).fit().summary()

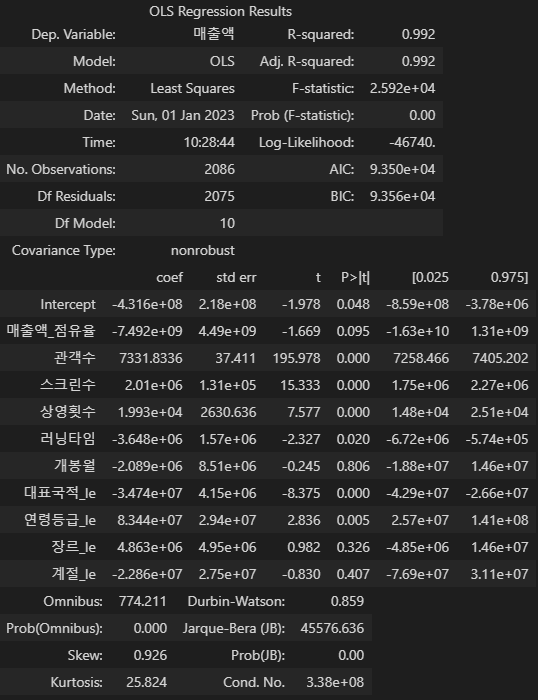
Df Residuals: 자유도(전체 표본 수 - 종속변수1개 - 독립변수10개)
Df Model: 독립변수의 개수
R-squared: 결정계수 --> 전체 데이터 중 해당 회귀모델이 설명할 수 있는 데이터의 비율, 회귀식의 설명력을 나타낸다.
Adj. R-squared: 회귀분석은 변수가 추가될 때 항상 설명력이 올라가기만 하기 때문에, 설명력에 영향이 거의 없는 변수라 할지라도 결과적으로 설명력을 높혀 모델의 설명력이 실제보다 높게 나올 수 있다. 따라서 독립변수의 개수에 따라 R-squared를 조정해줘야 한다.
F-statistics: F통계량을 뜻한다. F통계량은 MSR/MSE로 구할 수 있다. 도출된 회귀식이 통계적으로 유의한지 확인. 0에 가까울수록 좋음
Prob: F통계량에 해당하는 P-value를 의미한다. 회귀식이 유의미한지 확인. 0.05 이하일 경우 유의한 것으로 판단
Log-Likelihood: 로그우도, 생성된 모델이 주어진 데이터를 생성할 가능성의 수치적 기표. 모델을 생성하는 과정에서 각 변수에 대한 계수값을 비교할 때 사용
AIC, BIC: Log-Likelihood를 독립변수의 수로 보정한 값, 값이 작을 수록 좋음
- AIC: 표본의 개수와 모델의 복잡성을 기반으로 모델을 평가하며, 수치가 낮을 수록 좋음
- BIC: AIC와 유사하나 패널티를 부여하여 AIC보다 모델 평가 성능이 더 좋으며, 수치가 낮을 수록 좋음
Intercept coef: 회귀식의 절편값
각 column의 coef: 각 독립변수의 회귀계수(기울기)
std err: 계수의 표준오차(표본 통계량의 표준 편차), 값이 작을 수록 좋음
t: 독립변수와 종속변수간에 선형관계(관련성)가 존재하는 정도, 값이 클수록 상관도가 큼
- t 값이 크다 = 표준 편차가 작다 = 독립-종속변수 간 상관도 높음
- t 값이 작다 = 표준 편차가 크다 = 독립-종속변수 간 상관도 낮음
P>|t|: p-value(유의확률), 귀무가설이 맞다고 가정할 때 얻은 결과보다 극단적인 결과가 실제로 관측될 확률, 일반적으로 유의수준 5%보다 p값이 작으면(p < 0.05), “통계적으로 유의미하다”고 판단
Omnibus: 디아고스티노 검정(귀무가설 검정), 비대칭도와 첨도를 결합한 정규성 테스트, 값이 클수록 정규 분포를 따른다는 의미
Prob(Omnibus): 디아고스티노 검정이 유의한지 판단, 0.05 이하일 경우 유의하다고 판단
Skew: 왜도, 평균 주위의 잔차들의 대칭하는지를 보는 것이며, 0에 가까울수록 대칭
Kurtosis: 첨도, 잔차들의 분포 모양이며, 3에 가까울 수록 정규분포이다. (음수이면 평평한 형태, 양수는 뾰족한 형태)

모델링

Train, Test 분할

from sklearn.model_selection import train_test_split

X = df_ml.drop('매출액', axis=1)
y = df_ml['매출액']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=13)

학습

from sklearn.linear_model import LinearRegression

reg = LinearRegression()
reg.fit(X_train, y_train)

모델 평가 위한 RMS

from sklearn.metrics import mean_squared_error

pred_tr = reg.predict(X_train)
pred_test = reg.predict(X_test)

rmse_tr = np.sqrt(mean_squared_error(y_train, pred_tr))
rmse_test = np.sqrt(mean_squared_error(y_test, pred_test))
print('RMSE train : ', rmse_tr)
print('RMSE test : ', rmse_test)

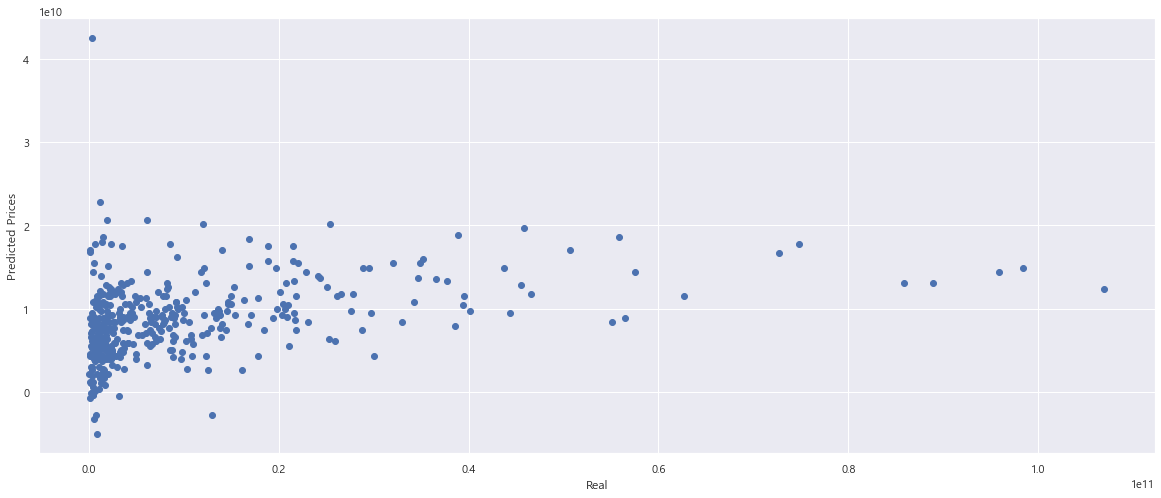
성능 확인

plt.scatter(y_test, pred_test)
plt.xlabel('Real')
plt.ylabel('Predicted Prices')
plt.plot([0, 1e+11], [0, 1e+11], 'r')
plt.show()

개봉월, 대표국적_le, 연령등급_le, 장르_le, 계절_le 제외하고 다시 수행

Train, Test 분할

from sklearn.model_selection import train_test_split

X = df_ml.drop(['매출액', '대표국적_le', '연령등급_le', '장르_le', '계절_le'], axis=1)
y = df_ml['매출액']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=13)

학습

from sklearn.linear_model import LinearRegression

reg = LinearRegression()
reg.fit(X_train, y_train)

RMS

from sklearn.metrics import mean_squared_error

pred_tr = reg.predict(X_train)
pred_test = reg.predict(X_test)

rmse_tr = np.sqrt(mean_squared_error(y_train, pred_tr))
rmse_test = np.sqrt(mean_squared_error(y_test, pred_test))

print('RMSE train : ', rmse_tr)
print('RMSE test : ', rmse_test)
plt.scatter(y_test, pred_test)
plt.xlabel('Real')
plt.ylabel('Predicted Prices')
plt.plot([0, 1e+11], [0, 1e+11], 'r')
plt.show()

print('모델 정확도 : ', reg.score(X_test, y_test))

스케일 적용하기

from sklearn.preprocessing import MinMaxScaler, StandardScaler, RobustScaler

mm = MinMaxScaler()
ss = StandardScaler()
rs = RobustScaler()

MinMaxScaler

mm.fit(X_train)
X_train_mm = mm.transform(X_train)
X_test_mm = mm.transform(X_test)
reg.fit(X_train_mm, y_train)
print('모델 정확도 : ', reg.score(X_test_mm, y_test))

StandardScaler

ss.fit(X_train)
X_train_ss = ss.transform(X_train)
X_test_ss = ss.transform(X_test)
reg.fit(X_train_ss, y_train)
print('모델 정확도 : ', reg.score(X_test_ss, y_test))

RobustScaler

rs.fit(X_train)
X_train_rs = rs.transform(X_train)
X_test_rs = rs.transform(X_test)
reg.fit(X_train_rs, y_train)
print('모델 정확도 : ', reg.score(X_test_rs, y_test))

스케일링을 진행해도 변화가 없다;;;

러닝타임과 매출액 correlation 0.3 따로 ML 수행

데이터 분할

from sklearn.model_selection import train_test_split

X = df_ml[['러닝타임']]
y = df_ml['매출액']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=13)

학습

from sklearn.linear_model import LinearRegression

reg = LinearRegression()
reg.fit(X_train, y_train)

RMS

from sklearn.metrics import mean_squared_error

pred_tr = reg.predict(X_train)
pred_test = reg.predict(X_test)

rmse_tr = np.sqrt(mean_squared_error(y_train, pred_tr))
rmse_test = np.sqrt(mean_squared_error(y_test, pred_test))
print('RMSE train : ', rmse_tr)
print('RMSE test : ', rmse_test)

plt.scatter(y_test, pred_test)
plt.xlabel('Real')
plt.ylabel('Predicted Prices')
plt.show()
print('모델 정확도 : ', reg.score(X_test, y_test))

실패....

XGBRegressor 적용

import xgboost

데이터 분할

X = df_ml.drop('매출액', axis=1)
y = df_ml['매출액']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=13)

학습

xgbr = xgboost.XGBRegressor(n_estimators=400, learning_rate=0.1, max_depth=3)
xgbr.fit(X_train, y_train)

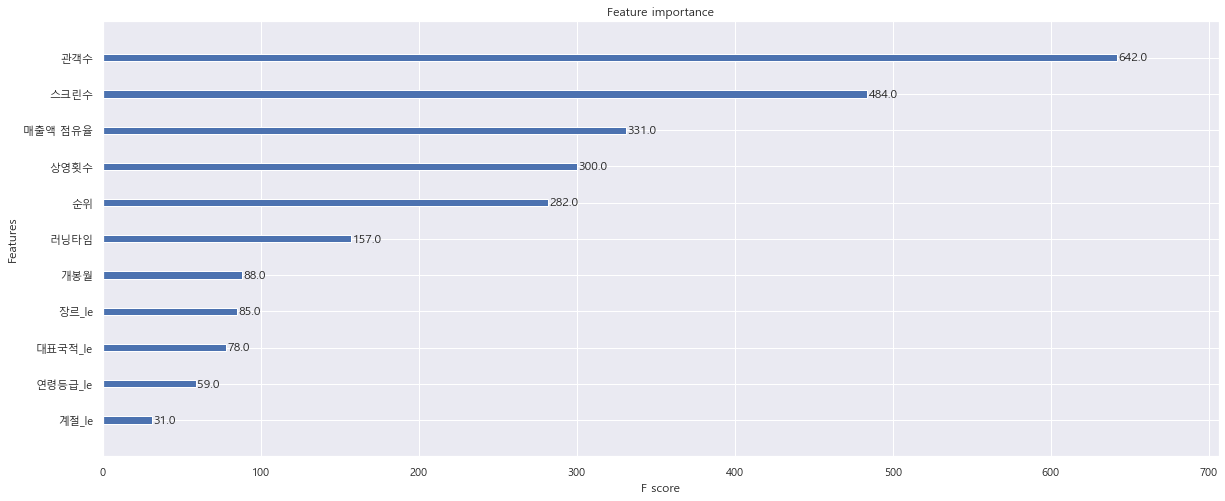
Column별 중요도

xgboost.plot_importance(xgbr)

예측

pred = xgbr.predict(X_test)
pred
r_sq = xgbr.score(X_train, y_train)
print(r_sq)

일반 reg모델과 비교하면, 0.991258에서 0.999564까지 스코어가 오른 것을 확인!

pred_tr = xgbr.predict(X_train)
pred_test = xgbr.predict(X_test)

rmse_tr = np.sqrt(mean_squared_error(y_train, pred_tr))
rmse_test = np.sqrt(mean_squared_error(y_test, pred_test))

print('RMSE train : ', rmse_tr)
print('RMSE test : ', rmse_test)
plt.scatter(y_test, pred_test)
plt.xlabel('Real')
plt.ylabel('Predicted Prices')
plt.plot([0, 1e+11], [0, 1e+11], 'r')
plt.show()

Theo Kim

THEO's velog

이전 포스트

네이버 영화 데이터 크롤링

다음 포스트

국내 박스오피스 영화 EDA & ML

데이터 준비

인덱스 재설정

중복 영화명에서 첫 영화 빼고 제거

영화 장르 첫 번째 빼고 다 제거

러닝타임 0분 조회

연령등급 확인

Label Encode

float로 변환

EDA

매출액에 대한 히스토그램

수치 확인

분포 확인

상관관계

OLS 분석

모델링

Train, Test 분할

학습

모델 평가 위한 RMS

성능 확인

개봉월, 대표국적_le, 연령등급_le, 장르_le, 계절_le 제외하고 다시 수행

Train, Test 분할

학습

RMS

스케일 적용하기

MinMaxScaler

StandardScaler

RobustScaler

러닝타임과 매출액 correlation 0.3 따로 ML 수행

데이터 분할

학습

RMS

XGBRegressor 적용

데이터 분할

학습

Column별 중요도

예측

네이버 영화 데이터 크롤링

Constants

0개의 댓글