문제해결 절차
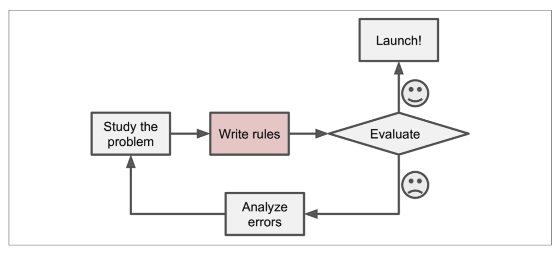
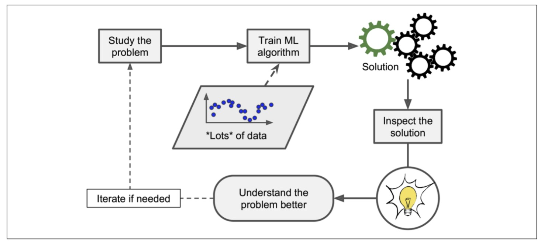
일반적인 문제해결 절차
데이터 기반 문제해결 절차
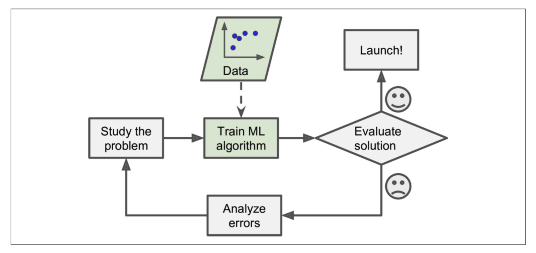
모델 스스로 데이터를 기반으로 변화에 대응
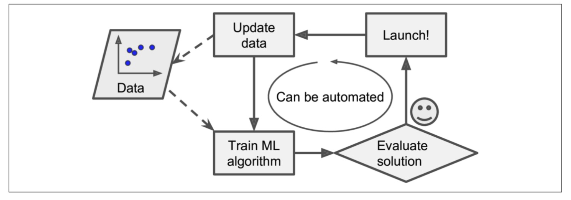
머신러닝을 통한 학습
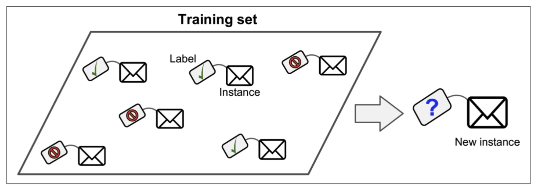
지도학습 - 분류 Classification
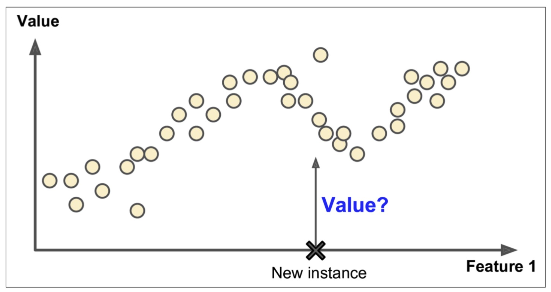
지도학습 - 회귀 Regression
비지도학습은 레이블 없다
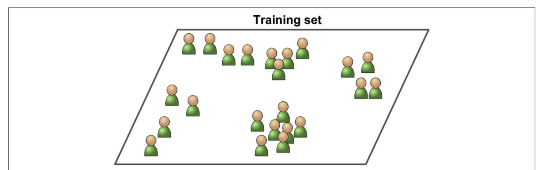
비지도학습 - 군집
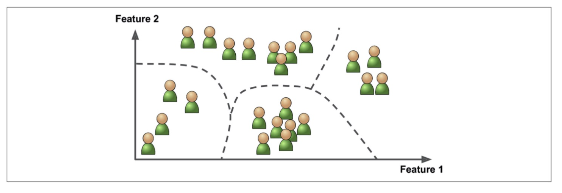
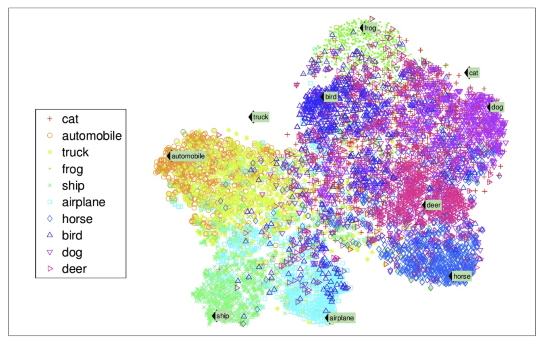
비지도학습 - 차원 축소
Regression 회귀
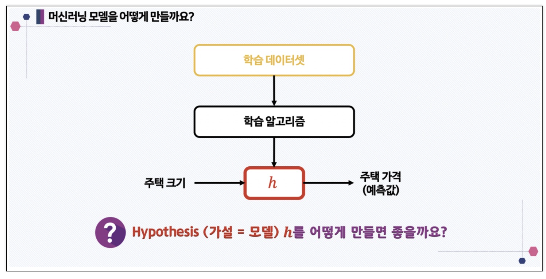
만약 주택의 넓이과 가격이라는 데이터가 있고 주택가격을 예측한다면
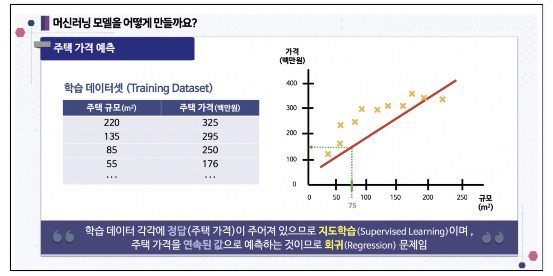
머신러닝 모델 만들기
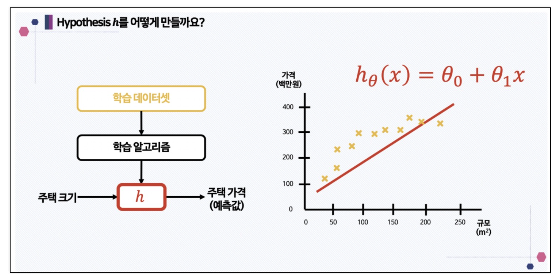
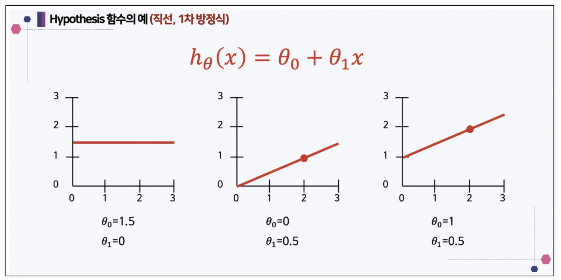
1차함수
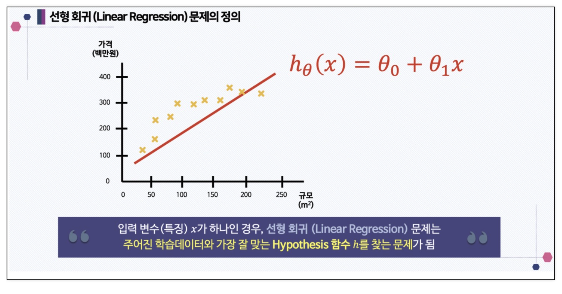
선형 회귀
모델을 구성하는 파라미터 찾기
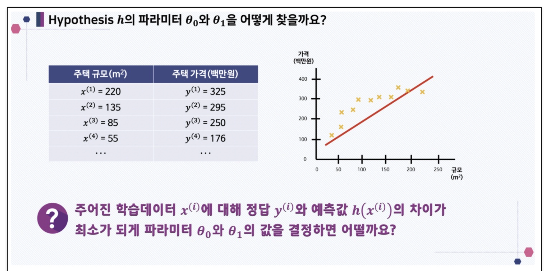
OLS (Ordinary Linear Least Square)
- 데이터를 하나의 직선으로 만든다면
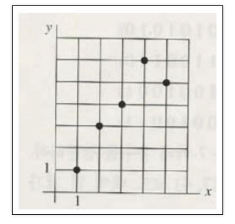
- 직선
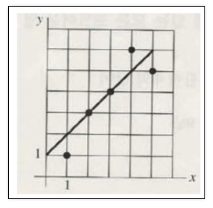
- 데이터를 모두 직선에 대입
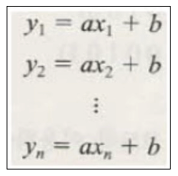
- 문제를 벡터와 행렬로 표현

- 찾고 싶은 모델
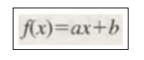
- 행렬로 정리
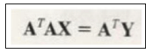
- 드디어 X를 찾을 수 있다

- 본래의 문제로
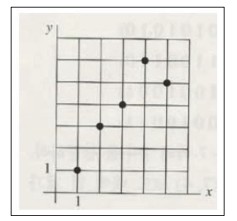
- 데이터로

- 원 식
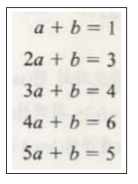
- 정리
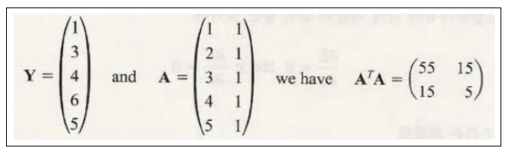
- 적용하면 a와 b를 구할수 있다

- 최종 모델
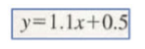
- 모델의 성능을 표현

실습
- pip install statsmodels
데이터 만들기
import pandas as pd
data = {'x':[1,2,3,4,5], 'y':[1,3,4,6,5]}
df = pd.DataFrame(data)
df
가설을 세우기
import statsmodels.formula.api as smf
lm_model = smf.ols(formula='y~x', data=df).fit()결과
lm_model.params
seaborn
import matplotlib.pyplot as plt
import seaborn as sns
sns.lmplot(x='x', y='y', data=df)
plt.xlim([0, 5])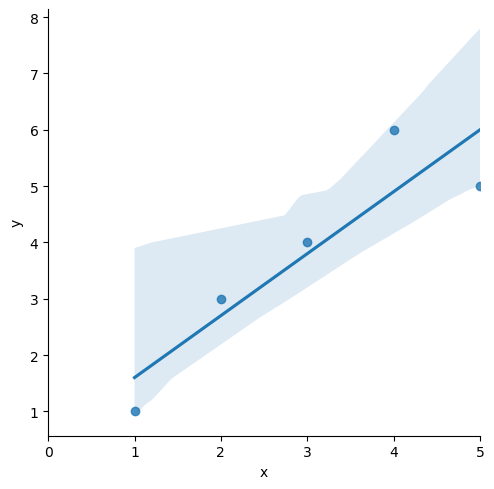
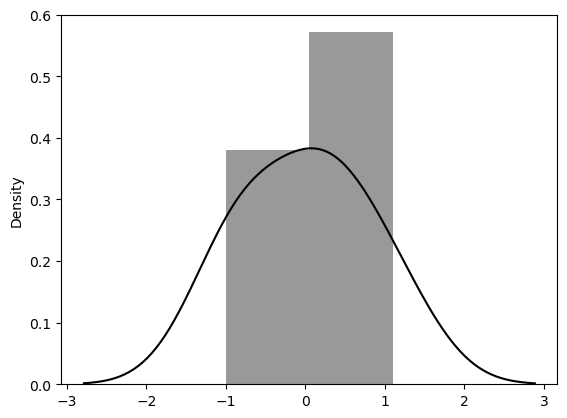
잔차 평가 residue
- 잔차는 평균이 0인 정규분포를 따르는 것 이어야 함
- 잔차 평가는 잔차의 평균이 0이고 정규분포를 따르는 지 확인
잔차 확인
resid = lm_model.resid
resid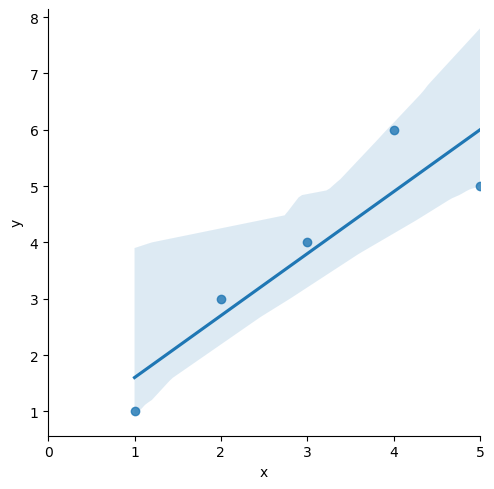
결정계수 R-Squared
- y_hat은 예측된 값
- 예측 값과 실제 값(h)이 일치하면 결정계수는 1이 됨(즉 결정계수가 높을 수록 좋은 모델)
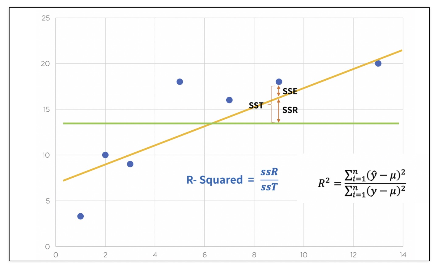
결정계수 계산 -numpy
import numpy as np
mu = np.mean(df['y'])
y = df['y']
y_hat = lm_model.predict()
np.sum((y_hat-mu)**2) / np.sum((y - mu)**2)
lm_model.rsquared
잔차의 분포도 확인
sns.distplot(resid, color='black')