Principal Component Analysis
PCA 란 ?

- 차원축소 (dimensionality)와 변수추출 (feature extraction) 기법으로 널리 쓰이고 있는 주성분분석 (Principal Component Analysis)
- PCA는 데이터의 분산 (variance)을 최대한 보존하면서 서로 직교하는 새 기저(축)를 찾아, 고차원 공간의 표본들을 선형 연관성이 없는 저차원 공간으로 변환하는 기법.
- 변수추출 (Feature Extraction)은 기존 변수를 조합해 새로운 변수를 만드는 기법. (변수선택(Feature Selection)과 구분할 것)
데이터를 어떤 백터에 정사영시켜 차원을 낮출 수 있음
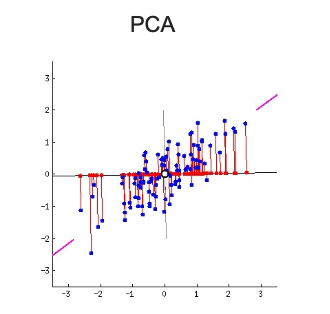
백터를 이용해서 데이터를 다시 표현
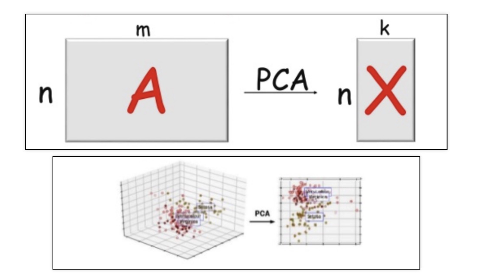
데이터를 변환시켰을 때, 어떤 백터를 선정하면 본래 데이터 구조를 가장 잘 유지할 수 있을까
데이터를 새로운 축으로 표현하는 것
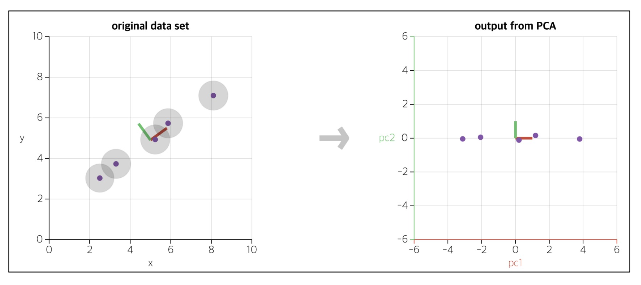
차원이 많은 경우 간단하게 표현해 볼 수 있다.
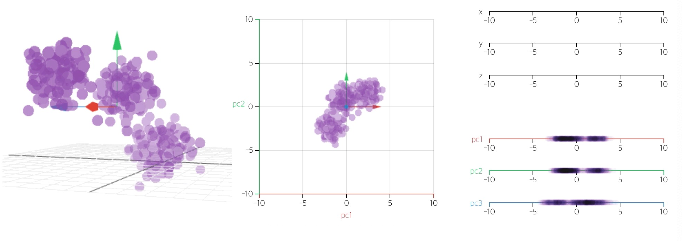
데이터
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
rng = np.random.RandomState(13)
X = np.dot(rng.rand(2,2), rng.randn(2,200)).T
X.shape
plt.scatter(X[:,0], X[:,1])
plt.axis('equal')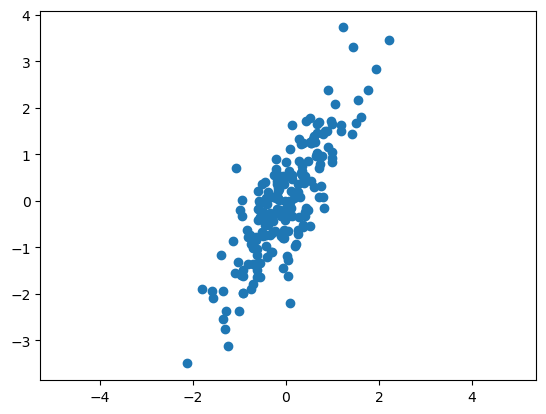
fit
from sklearn.decomposition import PCA
pca = PCA(n_components=2, random_state=13)
pca.fit(X)
벡터와 분산값
pca.components_
pca.explained_variance_
pca.explained_variance_ratio_
pca.mean_
주성분 백터
def draw_vector(v0, v1, ax=None):
ax = ax or plt.gca()
arrowprops = dict(arrowstyle="->",
linewidth=2, color="black",
shrinkA=0, shrinkB=0)
ax.annotate('',v1, v0, arrowprops=arrowprops)
plt.scatter(X[:,0], X[:,1], alpha=0.4)
for length, vector in zip(pca.explained_variance_, pca.components_):
v = vector * 3 * np.sqrt(length)
draw_vector(pca.mean_, pca.mean_ + v)
plt.axis('equal')
plt.show()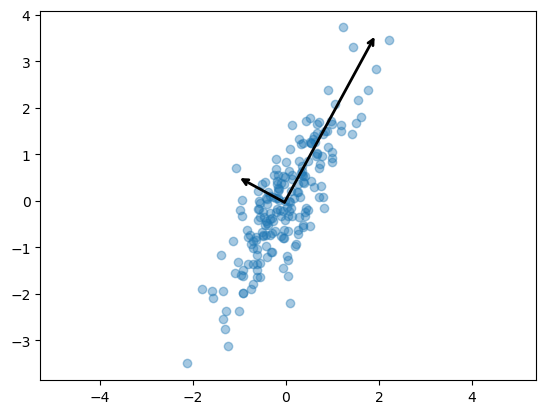
데이터의 주성분을 찾은 다음 주축을 변경하는 것도 가능
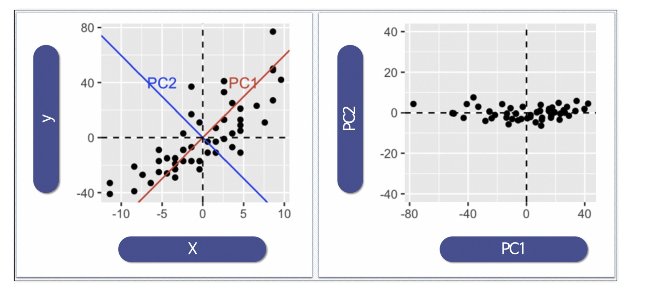
n_components를 1로 두고
pca = PCA(n_components=1, random_state=13)
pca.fit(X)
pca.components_
pca.mean_
pca.explained_variance_ratio_
X_pca = pca.transform(X)
X_pca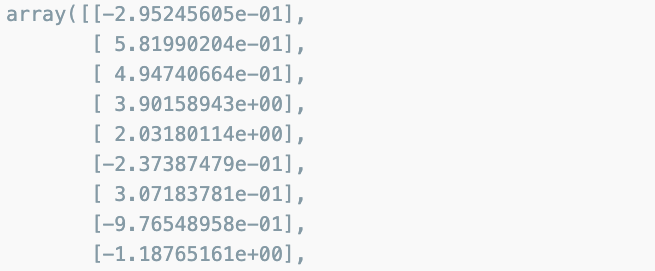
X_new = pca.inverse_transform(X_pca)
plt.scatter(X[:,0], X[:,1], alpha=0.3)
plt.scatter(X_new[:,0], X_new[:,1], alpha=0.9)
plt.axis('equal')
plt.show()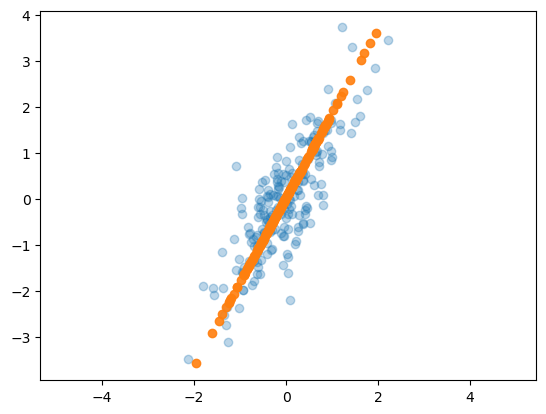
linear regression과 같은 결과 잎수도 있다.
Iris data
import pandas as pd
from sklearn.datasets import load_iris
iris = load_iris()
iris_pd = pd.DataFrame(iris.data, columns=iris.feature_names)
iris_pd['species'] = iris.target
iris_pd.head()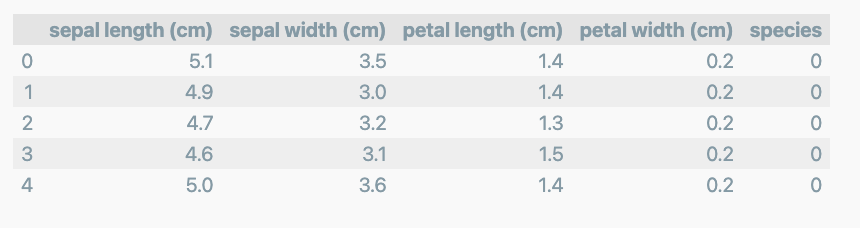
특성 4개를 한번에 확인하기는 어렵다
import seaborn as sns
sns.pairplot(iris_pd, hue='species', height=3,
x_vars=['sepal length (cm)', 'petal width (cm)'],
y_vars=['petal length (cm)', 'sepal width (cm)']);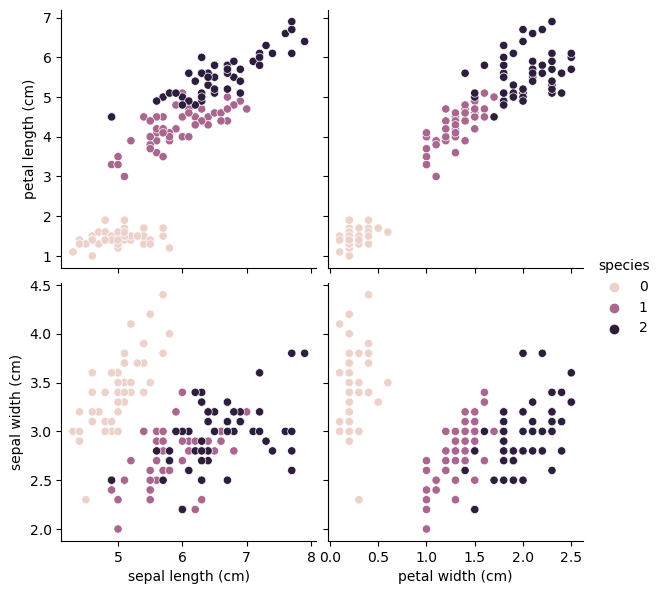
Scaler를 적용
from sklearn.preprocessing import StandardScaler
iris_ss = StandardScaler().fit_transform(iris.data)
iris_ss[:3]
pca 결과를 return 하는 함수
from sklearn.decomposition import PCA
def get_pca_data(ss_data, n_components=2):
pca = PCA(n_components=n_components)
pca.fit(ss_data)
return pca.transform(ss_data), pcareturn값 확인
iris_pca, pca = get_pca_data(iris_ss, 2)
iris_pca.shape 
pca.mean_
pca.components_
pca.explained_variance_ratio_
pca가 적용된 결과
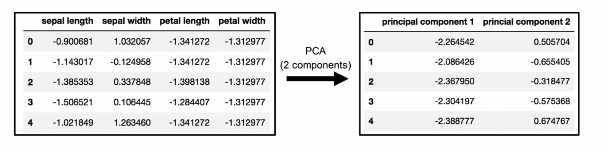
pca 결과를 pandas로 정리
def get_pd_from_pca(pca_data, cols=['PC1', 'PC2']):
return pd.DataFrame(pca_data, columns=cols)4개의 특성을 두 개의 특성으로 정리
iris_pd_pca = get_pd_from_pca(iris_pca)
iris_pd_pca['species'] = iris.target
iris_pd_pca.head()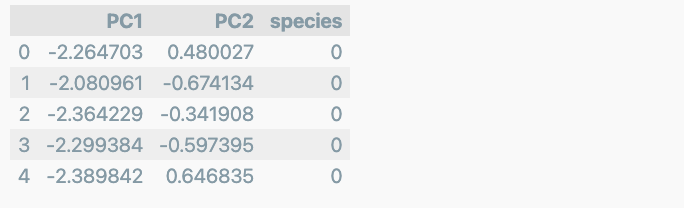
두개의 특성을 그리기
sns.pairplot(iris_pd_pca, hue='species',height=5, x_vars=['PC1'], y_vars=['PC2']);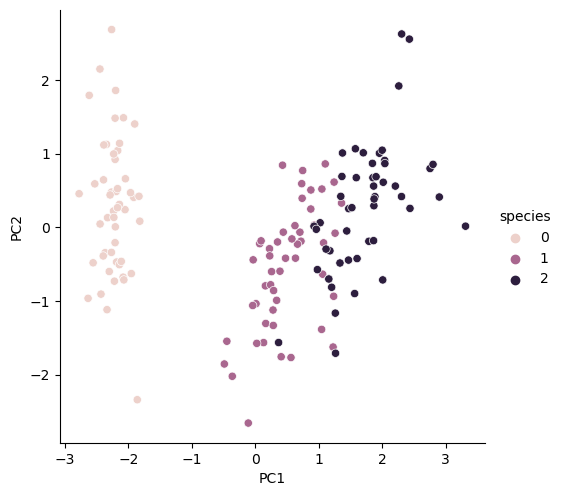
주성분 분석의 중요성
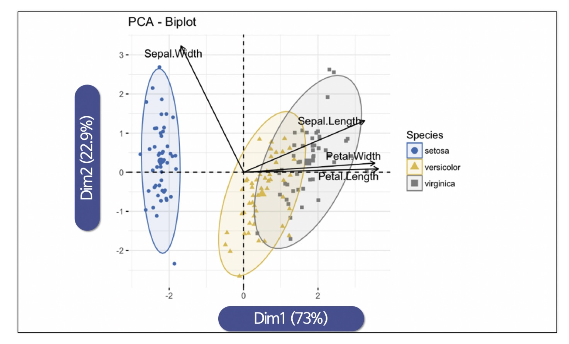
4개의 특성을 사용해서 randomforest에 적용하면
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
import numpy as np
def rf_scores(X, y, cv=5):
rf = RandomForestClassifier(random_state=13, n_estimators=100)
scores_rf = cross_val_score(rf, X, y, scoring='accuracy', cv=cv)
print('Score :', np.mean(scores_rf))
%%time
rf_scores(iris_ss, iris.target)
두개의 특성만 적용했을 때
pca_X = iris_pd_pca[['PC1', 'PC2']]
rf_scores(pca_X, iris.target) # 의미 없음 
Wine data
import pandas as pd
wine_url = 'https://raw.githubusercontent.com/PinkWink/ML_tutorial/master/dataset/wine.csv'
wine = pd.read_csv(wine_url, index_col=0)
wine.head()
와인 색상 분류
wine_X = wine.drop(['color'], axis=1)
wine_y = wine['color']StandardScaler 적용
wine_ss = StandardScaler().fit_transform(wine_X)def print_variance_ratio(pca):
print('varince_ratio :', pca.explained_variance_ratio_)
print('sum of varince_ratio :', np.sum(pca.explained_variance_ratio_))두개의 주성분으로 줄이는 건 데이터의 50%
pca_wine, pca = get_pca_data(wine_ss, n_components=2)
print_variance_ratio(pca)
pca_colums = ['PC1','PC2']
pca_wine_pd = pd.DataFrame(pca_wine, columns=pca_colums)
pca_wine_pd['color'] = wine_y.values
sns.pairplot(pca_wine_pd, hue='color', height=5, x_vars=['PC1'], y_vars=['PC2']);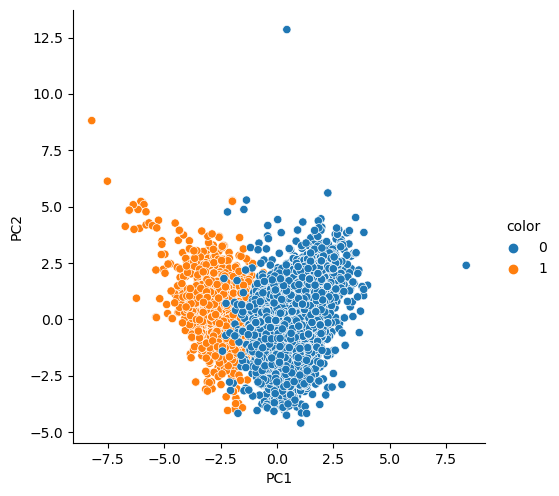
Random Forest에 적용했을 때 원 데이터와 큰 차이가 없다.
%%time
rf_scores(wine_ss, wine_y)
%%time
pca_X = pca_wine_pd[['PC1','PC2']]
rf_scores(pca_X, wine_y)
주성분 3개로 98%이상 표현할수 있다.
pca_wine, pca = get_pca_data(wine_ss, n_components=3)
print_variance_ratio(pca)
pca_colums = ['PC1','PC2','PC3']
pca_wine_pd = pd.DataFrame(pca_wine, columns=pca_colums)
pca_wine_pd['color'] = wine_y.values
pca_X = pca_wine_pd[pca_colums]
rf_scores(pca_X, wine_y)
주성분 3개로 표현한것을 정리
pca_wine_plot = pca_X
pca_wine_plot['color'] = wine_y.values
pca_wine_plot.head()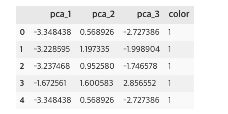
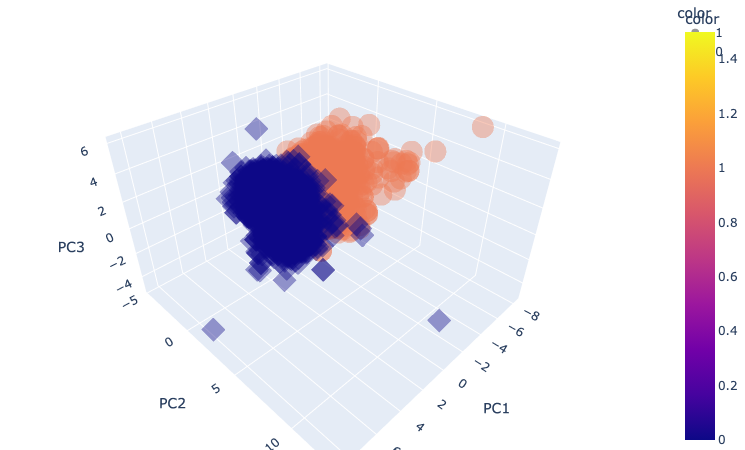
3D로 그리기
import plotly.express as px
fig = px.scatter_3d(pca_wine_plot, x='PC1', y='PC2', z='PC3', color='color', symbol='color', opacity=0.4)
fig.update_layout(margin=dict(l=0, r=0, b=0, t=0))
fig.show()