[Deep Reinforcement Learning] 2강 Markov property

👨‍🎓강의영상: https://www.youtube.com/watch?v=EtSNMoM97-k&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=2

1️⃣마코프 의사결정 과정

이번 강의에서는 Grid world model에 대해 배워볼 것이다.

2️⃣Grid world model이란?

우측 그림을 보면 가로가 4칸, 세로가 3칸인 격자(grid)구조를 확인할 수 있다. 해당 grid world에는 로봇이 있는데, 로봇이 우리가 학습시킬 agent이다.

Agent: 강화학습을 통해서 스스로 학습하는 대상.

🤙기본적인 규칙은 아래와 같다.

1. 로봇은 Grid의 경계선 밖으로 나갈 수 없다.

2. 로봇은 (2, 2)처럼 벽이 있는 곳에 존재할 수 없다.

3. $Random \ variable \ S$는 로봇의 위치를 의미한다.

   • S = {s | (1, 1), (2, 1) … , (4, 3)}
   • N(S) = 11, $Random \ variable \ S$가 취할 수 있는 경우의 수는 11개

4. 로봇은 1칸씩 이동한다.

   • State가 인접한 State로만 이동 가능하다는 의미.

5. 두가지 종류의 Reward가 존재한다.
   1) Big reward: 목표 달성 여부에 대한 직접적인 피드백

   • 목표 달성 시 +1
   • 목표 실패 시 - 1

   2) Small negative reward: '시간 경과' 또는 '비효율적인 행동'에 대한 페널티

   • 각 step마다 작은 negative 보상이 주어진다.
     

   예를 들어 agent가 6번 이동하여 목표 지점에 도달했다면 목표 도달 전까지 5번의 이동에 대하여 Small negative reward가 각각 적용되어 5c를 받는다. 이후 최종 이동에 대한 Big reward로 +1을 받아 total reward 5c + 1이 된다.

6. agent는 항상 계획대로 움직이지 않는다. 특정 확률로 예상치 못한 행동을 한다. 이를 noisy movement라 한다.

   • 위 자료에서 east 10%로 작성된 것을 확인할 수 있는데, agent가 원래는 south로 이동하려 했으나 10%확률로 east로 이동한 것을 확인할 수 있다.
   • 단 원래 계획의 반대 방향으로 행동하지는 않는다. 원래 목표가 north라면 south로는 절대 이동하지 않는다.

Agent는 하나의 state에서 action을 통해 다른 state로 움직이는 데, 이를 state transition 이라 한다.

강화학습의 최종 목표는 각 state에서 action을 정해주면, 최종 reward의 합이 최대화하는 것을 목표로 한다.

각 state마다 어떤 action을 취할 지 결정하는 것이 policy이고, total reward를 최대화 하는 policy를 optimal policy라 한다. 강화학습의 목표는 optimal policy를 찾는 것이다.

3️⃣Action을 적용하는 서로 다른 방법

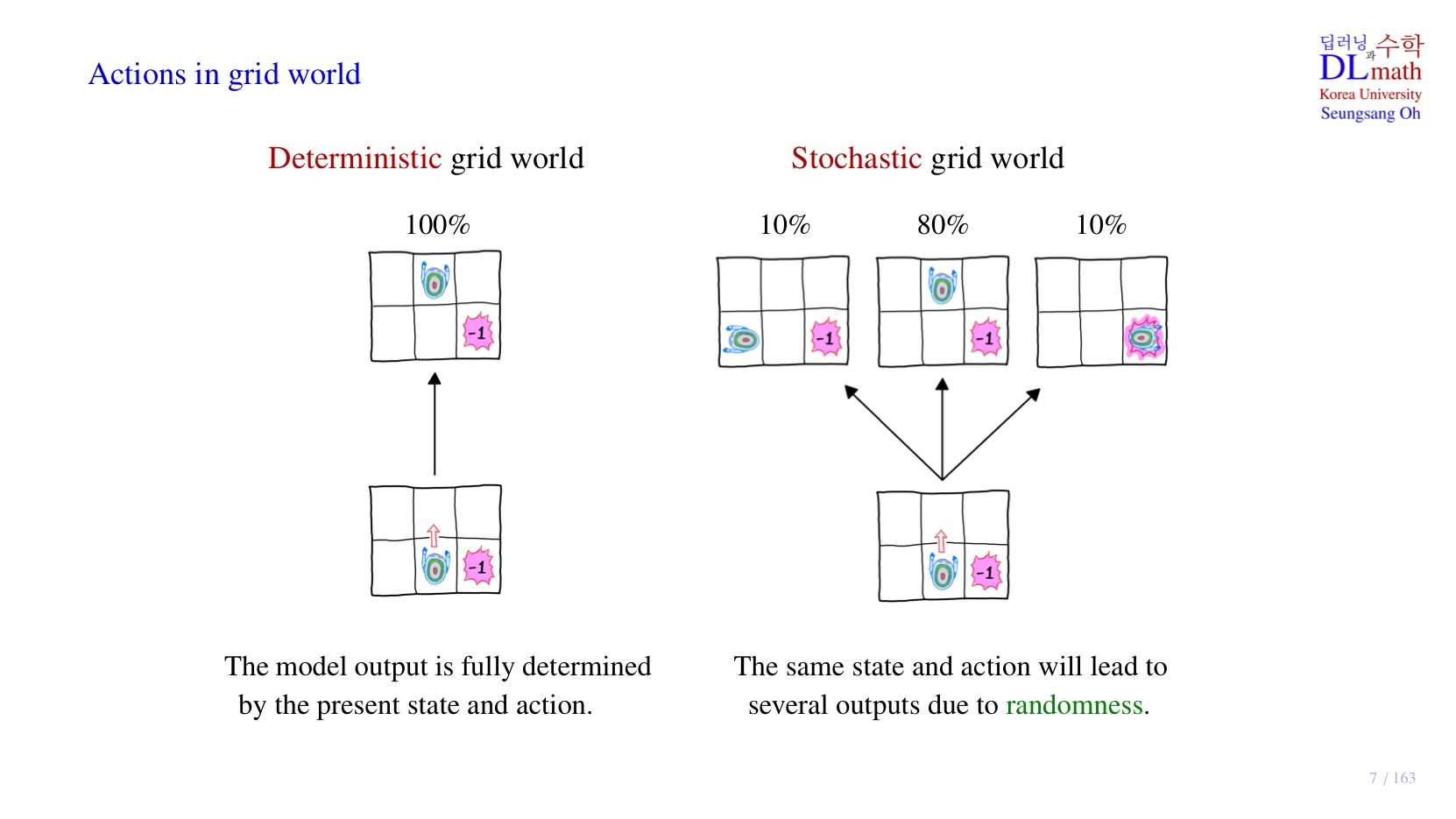
1. Deterministic

• 어떤 action을 취하려고 할 때, 실제로 해당 action을 취할 확률이 100%인 경우.
• 다른 행동을 할 noise가 존재하지 않는다.
• 결정한 대로 action이 취해지기 때문에 Deterministic이라고 부른다.
• 현재의 state와 action이 주어지면, 그 결과가 정확하게 출력된다.
• 학습이 완료되면 policy가 정해지는데, 이때 각 state에서 agent가 행동할 episode는 1가지이다.
• 입력과 출력이 확실한 함수의 형태이다.

2. Stochastic

• 어떤 action을 취하려고 할 때, 모델이 해당 action을 취할 확률이 100%가 아닌 경우.
• 다른 행동을 할 noise가 존재한다.
• 다시 말해, 원하는 대로 움직이지 않을 가능성이 존재한다.
• 다른 행동을 할 확률을 가지고 action이 취해지기 때문에 stochastic이라고 부른다.
• agent에 동일한 state와 action이 주어져도, 항상 동일한 결과가 출력되지 않는다.
• 학습이 완료되면 policy가 정해지는데, 이때 각 state에 대한 agent가 보일 episode는 다양하다.
• 다양한 경우가 발생할 수 있기 때문에 다양성이 확보된 것 같다.

✍정리

결국 각 방식은 모델이 보일 episode의 경우의 수를 결정하는데, 강화학습에서는 stochastic 방식을 사용한다.

4️⃣markov property

위의 stochastic 방식대로라면 모델이 어떤 state에서 취할 수 있는 각 action에 대하여 특정 확률을 가진다. 이를 염두해두며 markov decision process의 핵심 개념인 markov property에 대해 알아보자.

기본 개념

• $Random \ variable \ X$에 대하여 $P(X=3)$는 $X$가 3일 확률을 의미한다.
• stochastic process는 random variable의 collection이다.
• 이렇게 random variable이 모이면 각 random variable을 구분하기 위해 index를 지정할 수 있는데, 대표적인 index 방법이 시간에 따른 indexing 방법이다.
• 우리는 state를 나타내는 random variable를 사용할 것이기 때문에, random variable을 $S$로 표기한다.
  • past state: $S_0 \sim S_{t-1}$
  • present state: $S_t$
  • future state: $S_{t+1}$
• $t$의 종류에 따른 구분
  • $t$가 정수일 때: discrete time
  • $t$가 실수일 때: continuous time
  • 해당 강의에서는 discrete time random variable을 다룰 예정이다.

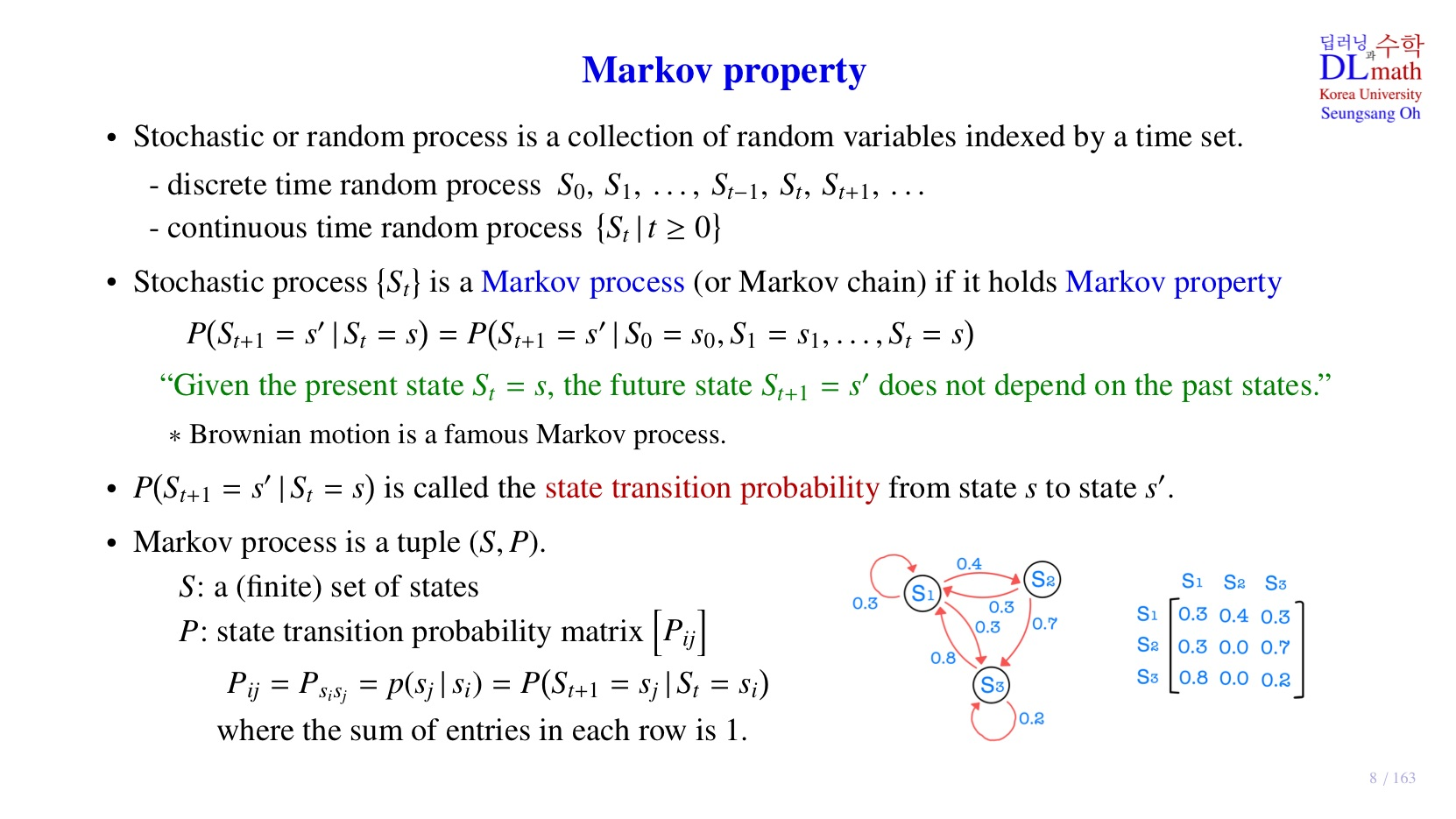
stochastic process가 Markov property를 따르면 Markov process라고 부른다.

Markov property란?

1. 일반적으로 공을 굴릴 때

• 만약 우리가 past state와 present state를 알고 있다면, future state를 예측하기 쉬울 것이다.
• 그런데 우리가 present state만 알고 있으면 어떨까? 그렇다면 future state를 예측하는 것은 쉽지 않을 것이다. 왜냐하면 future state는 present state 뿐만 아니라 past state의 영향도 받기 때문이다.

2. 그런데 만약 공의 질량이 0이라고 상상하면

• 공을 굴리더라도 방향이 언제든지 바뀔 수 있다.
• 즉 future state는 present state를 시작점으로 두되, past state의 영향을 받지 않는다.
• stochastic한 경우

Brownian motion: 액체나 기체 속에 떠 있는 미세 입자들이 불규칙하고 무질서하게 움직이는 현상

$P(S_{t+1} = s' | S_t = s) = P(S_{t+1} = s' | S_0 = s_0, S_1 = s_1, ..., S_t = s)$

따라서 위 수식에서 future state는 present state에만 조건부로 영향을 받고, past state는 조건부로 영향을 받지 않는다. 우변에서 $s_0, s_1$ 등에 어떤 값을 넣어도 확률 $P$는 변하지 않을 것이다.

이렇듯 과거의 상태에는 영향을 받지 않고, 오직 현재의 상태에만 영향을 받는 성질을 Markov property라고 한다.

과거의 과정, 기억이 필요하지 않기 때문에 Memoryless property라고 한다.

🤔내 생각

과거의 기억을 가져가지 않는 것은 현재에만 집중해서 최선의 선택을 하는 건가?? 과거의 기억을 가져가지 않기 때문에 메모리, 연산량 측면에서는 효율적일 수 있지만 좋은 성능을 보일 수 있을까?

state transition probability

: 하나의 상태에서 다른 상태로 이동하는 구조를 가진 확률

$P(S_{t+1} = s' | S_t = s)$

해당 확률 값을 조정한다는 것은 모델이 특정 상태 $S_t$에서 어떤 선택(action)을 할 지 결정하는 과정에 영향을 끼친다. 모델을 학습한다는 것은 agent가 우리가 원하는 대로 행동할 수 있도록 확률값을 조정하는 과정이다.

따라서 Markov process는 각 state와 state를 연결하는 확률인 state transition probability로 구성되어 있다.

위 자료의 행렬은 아래처럼 state transition probability로 표현할 수 있다.

$\begin{bmatrix} P(S_{t+1} = S_1 | S_t = S_1) & P(S_{t+1} = S_2 | S_t = S_1) & P(S_{t+1} = S_3 | S_t = S_1) \\ P(S_{t+1} = S_1 | S_t = S_2) & P(S_{t+1} = S_2 | S_t = S_2) & P(S_{t+1} = S_3 | S_t = S_2) \\ P(S_{t+1} = S_1 | S_t = S_3) & P(S_{t+1} = S_2 | S_t = S_3) & P(S_{t+1} = S_3 | S_t = S_3) \end{bmatrix}$

• 행의 합이 1인 이유는 각 행의 조건, 즉 현재 state가 action을 취했을 때, 도달할 수 있는 state를 모두 표현했기 때문에 최종 확률 합은 1이다.

🤔내 생각

만약 Markov property를 따르지 않는다면 어떻게 될까? 그렇다면 앞의 경우를 모두 고려해야 할 것이다. 우리가 사용하는 LLM 모델이 대표적인 Markov property를 따르지 않는 경우이다.

5️⃣정리

2강에서 배운 내용은 아래와 같다.

1. Grid world model의 기본 개념
2. Agent, State, Reward, Policy의 개념
3. Stochastic 방식의 Action 결정 방식
4. Markov Property
5. State transtion probability