👨‍🏫학습목표

Markov Decision Process의 정의와 Grid world model의 optimal policy에 대해 배워볼 예정이다.

👨‍🎓강의영상: https://www.youtube.com/watch?v=S-7lXVpFci4&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=3

1️⃣ Markov Decision Process의 정의

Markov Decision process(마르코프 의사결정 과정)

: 강화학습을 구현하는 기본적인 수학적 모델

📕지난시간에 배운 개념

1. Stochastic process

• Random variable의 collection, sequence

• Stochastic process의 state를 연결해주는 확률, 하나의 state에서 다른 state로 이동할 확률
  
  

2. Markov property

• 과거의 상태가 미래에 영향을 미치지 않는 것이다.

• Markov property를 따르면 확률이 위와 같이 정의할 수 있다.
• State transition probability라고 한다.
  
  

3. Stochastic process

• stochastic process가 Markov property를 만족하게 된 경우.
• Markov process는 $(S, P)$로 정의된다.
• $S$ : state
• $P$ : State transition probability

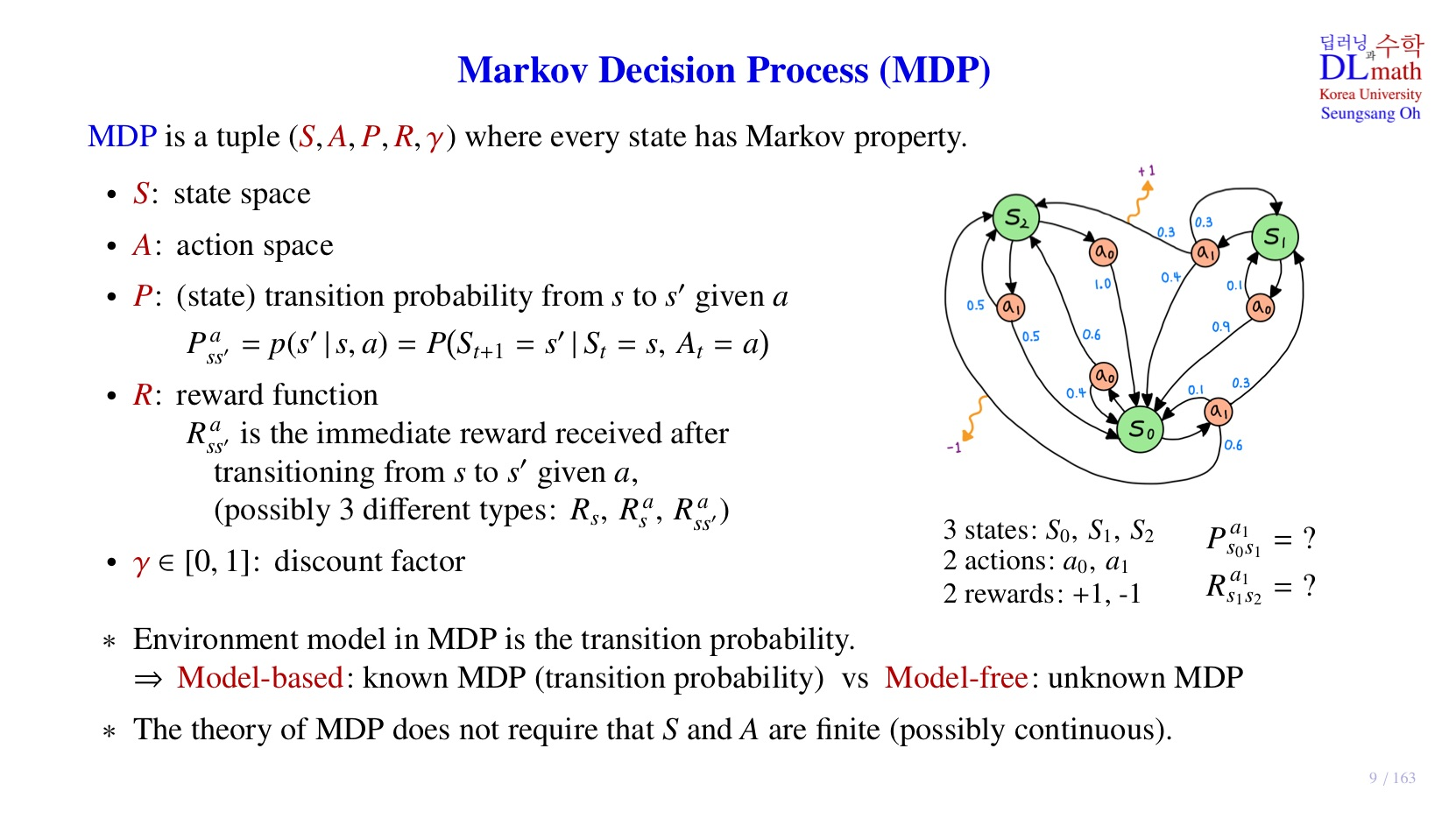
💡Markov Decision Process (MDP)의 정의란?

• $(S, A, P, R, \gamma)$로 정의된다.

• Markov process에서 $A, R$이 추가된 개념이다.

• $S$ : state space, agent가 현재 환경에서 인식하고 있는 상태 ,자기 자신의 상태, 외부 환경의 영향을 고려한 현재 상황.

• $A$ : action space, agent가 각 state에서 취할 수 있는 action의 집합

• $P$ : transition probability from $s$ to $s'$ given $a$

  $P^a_{ss'} = p(s' | s, a) = P(S_{t+1} = s' | S_t = s, A_t = a)$

  현재 state에서 미래의 state로 이동할 때, 현재 어떤 action을 취하는지를 반영한 확률.
  

• $R$ : reward function, 현재 state와 action에서 미래의 state로 이동했을 때 얻게 될 reward 의미.

  • $R_s$ : 현재 state에 머무를 때 받는 reward
  • $R^a_{s}$ : 현재 state에서 action을 취했지만, 계속 그 state에 머무를 때 받는 reward
  • $R^a_{ss'}$ : 현재 state에서 action을 취하여 다른 state로 이동할 때 받는 reward

• $\gamma$ : discount factor, 감가율. 다음 수업에서 다뤄보도록 하겠다.

✍정리

Markov Decision Process는 Markov process에서 어떤 action(선택)을 할지, 또 해당 선택에 대한 reward가 추가된 개념이다.

🔗Model based vs Model free

우리가 MDP 모델을 만들려면, $S, A, R$ 공간을 먼저 정의해야 한다.
이후 각 space 원소에 대한 connection, 즉 $P$ 값을 구해야 하는데, 상황에 따라 $P$를 구하는 것이 쉬울 수도, 어려울 수도 있다.

1. Model-based: known MDP

• transtion probability를 쉽게 알 수 있는 경우.
• 모델이 어떤 행동을 할 지 예측할 수 있기에 모델에 대해 안다고 할 수 있다.
• 모든 transition probability를 고려하여 모델의 행동 계산.
• Dynamic programming 사용.

Dynamic programming: 한번 푼 문제는 저장해뒀다고 나중에 계산 없이 사용.

2. Model-free: unknown MDP

• transtion probability를 쉽게 알 수 없는 경우
• model이 어떤 행동을 할 지 예측할 수 없기에 model에 대해 안다고 할 수 없다.
• transition probability를 알 수 없기에 sample data에 의존하여 policy 계산
• Reinforcement learning: 실제 환경이나 시뮬레이션 data를 활용하여 transition probability를 대체하여 policy 계산.

2️⃣ Grid world를 Markov Decision Process로 표현

1. Stochastic State transition probability

• 현재 state와 action이 주어지더라도 원하는 state에 100% 도달하는 것은 아니다.
• 특정 확률로 다른 state에 도달할 확률 역시 transition probability에 작성해야 한다.

2. 정의 가능한 state transition probability의 수

• 가능한 현재 state의 수: 9가지, (4,2), (4, 3)에 도달하면 모델이 종료되기 때문에 제외.
• 가능한 action: 4가지
• 미래의 state: 11가지
• 총 가능한 transition probability의 수 : $9 \times 4 \times 11$
• 단, 모델이 한번에 2칸을 이동할 수 없기 때문에, 총 가능한 transition probability 중 많은 경우는 0일 것이다.

3. Reward

• Big reward는 action과 관계없이, 미래의 state에 의해 결정된다.
• Big reward를 제외한 모든 경우는 small negative reward 부여.

3️⃣ Optimal policy 구하기

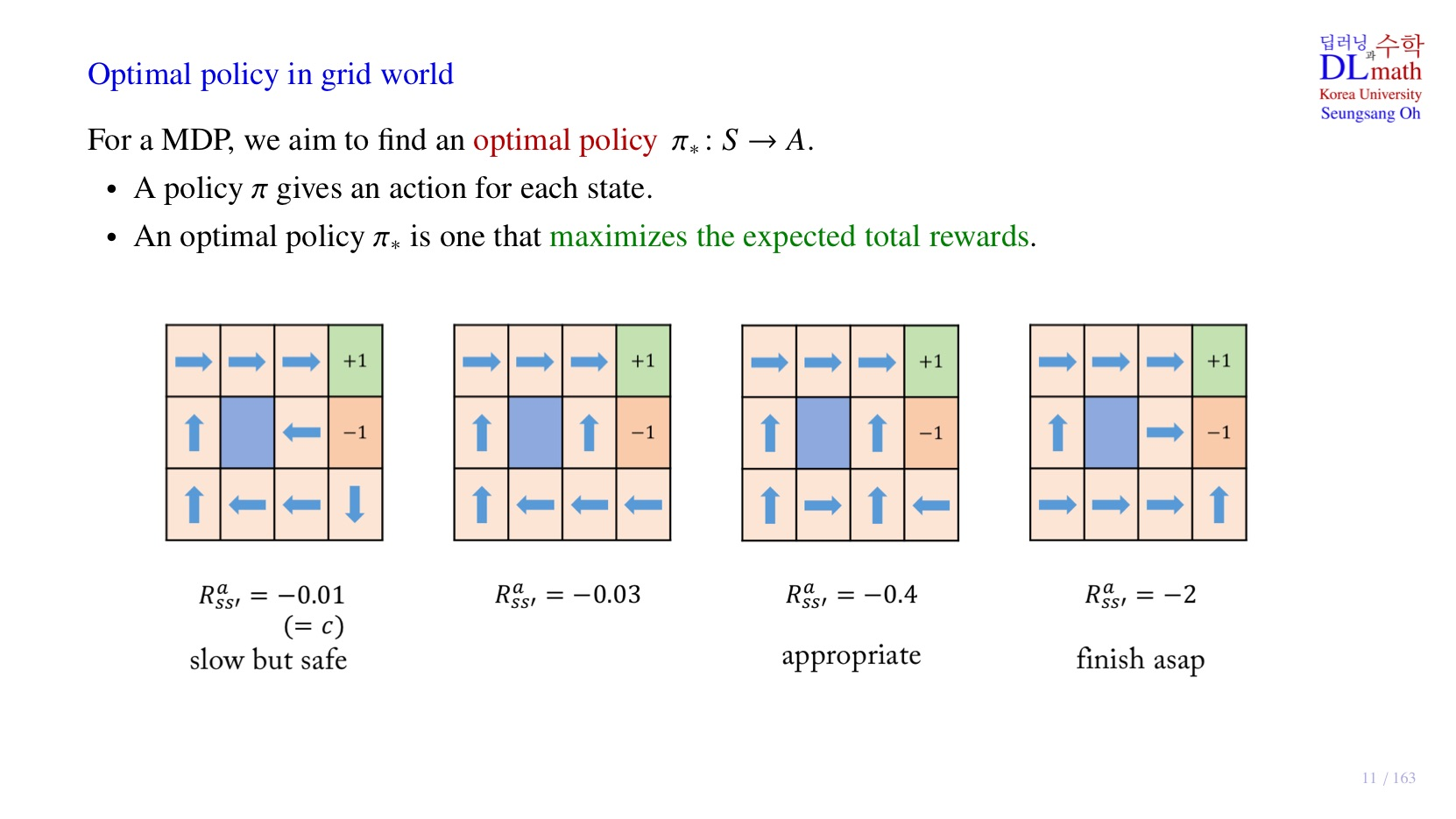
1. Small negative reward에 따른 policy

위 자료는 small negative reward로 $-0.01, -0.03, -0.4, -2$, 4가지를 각각 부여한 경우이다.

2. $\pi$ : policy

• $S \rightarrow A$

• 각 state에서 어떤 action을 취해야 하는지 결정해주는 것.

🤔내 생각

Small negativie reward의 절대값이 커질수록 model의 행동이 점점 더 대범해지는 것 같다.
$R^a_{s's'} = -0.4$ 인 경우 모델이 (3,1)에서 자칫 잘못하면 stochastic하게 실수하여 $-1$ reward를 받을 수 있지만 직진하는 것을 확인할 수 있다. 안전하게 돌아갈 때의 small negative reward가 더 손해이기 때문이다.

💡optimal policy

$R^a_{s's'} = -0.4$ 인 경우, action이 stochastic하기 때문에, 해당 화살표를 갖는 action에서도 다양한 episode가 등장한다.

1. 우측 상단으로 2칸 이동 후 오른쪽으로 이동하여 +1에 도달한 경우: 4c + 1 = -0.6
2. 우측으로 2칸, 위로 1칸, 우측으로 1칸 이동하여 -1에 도달한 경우: 3c -1 = -2.2

각 policy를 평가하기 위해..

• 가능한 모든 episode의 reward의 기대값을 계산하여 최종 reward 계산.
• Expected total reward를 maximize하는 화살표를 optimal policy로 결정한다.
• 각 small negative reward마다 optimal policy를 갖는다.

4️⃣ 정리

3강에서 배운 내용은 아래와 같다.

1. Markov Decision Process의 개념.
2. Model-free: unknown MDP는 데이터를 통해 Policy 설계.
3. Small negative reward에 따른 model의 행동 변화.
4. optimal policy를 정하기 위한 Expected total reward 계산.