👨‍🏫학습목표

오늘은 Temporal Difference Learning과 그 종류 Sarsa, Q-learning에 대해 배워볼 예정이다.

👨‍🎓강의영상: https://www.youtube.com/watch?v=5Vbn4XoE45w&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=13

1️⃣ Temporal Difference Learnings (TD)

🔷 Temporal Difference Learning

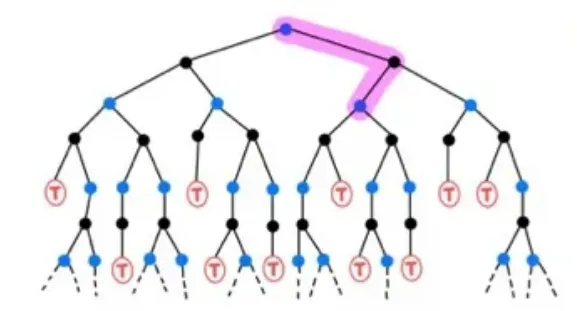
• Transition probability가 주어져 있지 않은 model-free 방식이다.
• Monte Carlo 방식처럼 GPI 방식을 사용하지만 하나의 episode가 아닌 다음 state 단위로 Q-value를 업데이트한다.
• 기존의 방식대로 Table을 만들어 업데이트 하는 방식이다.

🔻 Temporal Difference Learning의 장점

• Bootstrapping: State function을 업데이트 할 때, 다른 state function의 추정치를 활용하여 추정한다.

• 데이터를 sampling하여 사용하기 때문에 next-state transition probability를 몰라도 학습 가능하다.

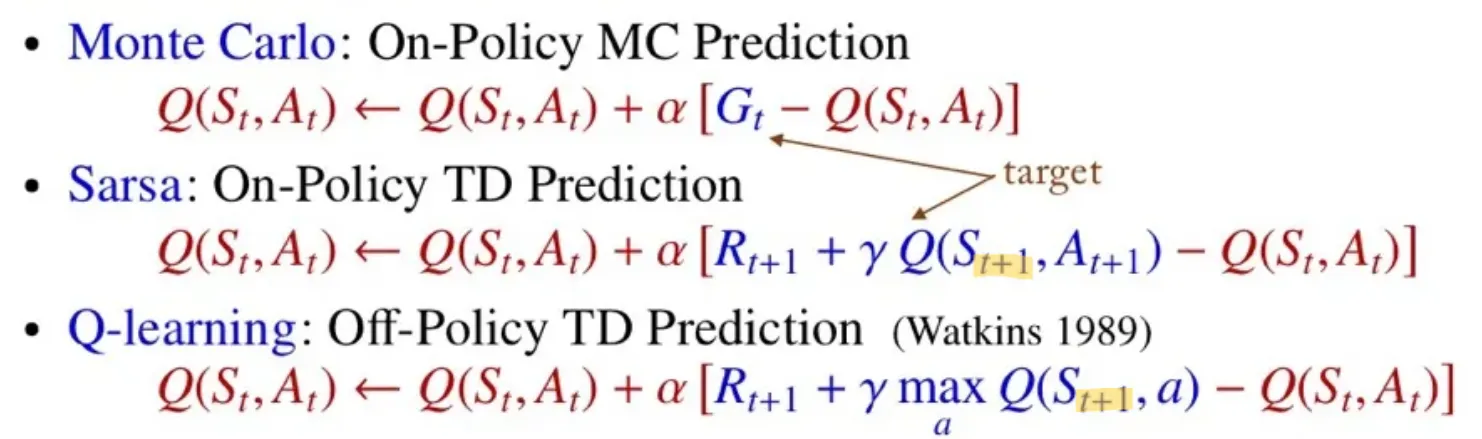
🔷 각 방식의 Policy Evaluation 비교

🔻 Monte Carlo

$Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha [G_t - Q(S_t, A_t)]$

• Return $G_t$를 사용하여 업데이트를 한다.

🔻 Sarsa

$Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha [R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t)]$

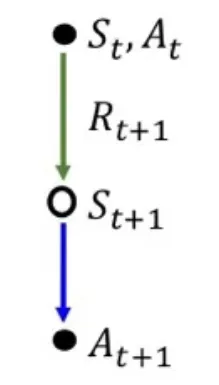
• Sample data: $(s_t, a_t, r_{t+1}, s_{t+1}, a_{t+1})$
• 현재 state와 action에서 얻게 되는 Reward $R_{t+1}$과 다음 state-action에 대한 Q-value $Q(S_{t+1}, A_{t+1})$를 사용하여 업데이트를 한다.
• 실제로 sample에서 모델이 실행한 action의 $Q(S_{t+1}, A_{t+1})$을 사용한다.
• $Q(S_{t+1}, A_{t+1})$을 사용한다는 것은 모델의 학습에서 stochastic한 부분을 반영하겠다는 의미이다.
• 더 다양한 경험을 하여 미래에 발생할 수 있는 상황에 대한 정보가 풍부하다.
• Bellman expectation equation을 통해 학습한 것이다.
• Current policy를 기반으로 학습한 것이다.

$q_\pi(s, a) = \mathbb{E}_\pi[R_{t+1} + \gamma q_\pi(S_{t+1}, A_{t+1}) | S_t = s, A_t = a]$

🔻 Q-learning

$Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha [R_{t+1} + \gamma \max_a Q(S_{t+1}, a) - Q(S_t, A_t)]$

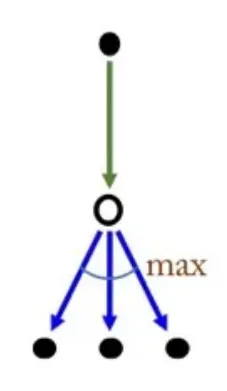
• Sample data: $(s_t, a_t, r_{t+1}, s_{t+1})$
• 현재 state와 action에서 얻게 되는 Reward $R_{t+1}$과 다음 state-action에 대한 Q-value $Q(S_{t+1}, A_{t+1})$ 중 그 값이 최대가 되게 하는 $\max_a Q(S_{t+1}, a)$를 사용하여 업데이트를 한다.
• $\max_a Q(S_{t+1}, a)$를 사용한다는 것은 현재 모델이 sample로 어떤 선택은 한지와 관계없이 Q-value값이 가장 큰 action을 취했다고 가정하고 업데이트를 진행한다.
• $\max_a Q(S_{t+1}, a)$를 선택하는 것은 현재 policy에서 최대한 좋은 action을 선택하겠다는 deterministic한 성격을 띄고 있다.
• 항상 이상적인 최적의 선택만 하기 때문에 위험한 상황에 어떻게 대처할지에 대한 학습이 부족하다.
• Sarsa보다는 Q-learning을 적용했을 때 더 좋은 성능이 나왔다는 연구 결과가 있다.
• Bellman optimal equation을 통해 학습한 것이다.
• Optimal policy를 기반으로 학습한 것이다.

$q_*(s, a) = \mathbb{E}[R_{t+1} + \gamma \max_{a'} q_*(S_{t+1}, a') | S_t = s, A_t = a]$

---

2️⃣ Sarsa & Q-learning의 pseudo code

🔷 Sarsa pseudo code

🔻 1. Initialize

• $Q(S,A)$를 모두 초기화하고 마지막 $Q(S,A)$는 0으로 초기화한다.
• Terminal state 이후에는 model의 행동이 종료되기 때문이다.

🔻 2. Policy Evaluation

• 시작 state $S_0$을 정한다.
• 시작 state $S_0$에서 모델의 $\epsilon$-greedy policy에 따라 $a_0$를 선택한다.
• model이 실제 경험을 하며 $R_{1}$과 $S_{1}$에 대한 data를 수집한다.
• $S_{1}$에서 모델의 $\epsilon$-greedy policy에 따라 $a_1$를 선택한다.

🔻 3. Policy Imprevoment

$Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha [R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t)]$

• Q-value를 수집한 데이터를 통해 업데이트한다.

🔷 Q-learning pseudo code

🔻 1. Initialize

• $Q(S,A)$를 모두 초기화하고 마지막 $Q(S,A)$는 0으로 초기화한다.
• Terminal state 이후에는 model의 행동이 종료되기 때문이다.

🔻 2. Policy Evaluation

• 시작 state $S_0$을 정한다.
• 시작 state $S_0$에서 모델의 $\epsilon$-greedy policy에 따라 $a_0$를 선택한다.
• model이 실제 경험을 하며 $R_{1}$과 $S_{1}$에 대한 data를 수집한다.

🔻 3. Policy Improvement

$Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha [R_{t+1} + \gamma \max_a Q(S_{t+1}, a) - Q(S_t, A_t)]$

• $\max_a Q(S_{t+1}, a)$를 통해 업데이트한다.

---

3️⃣ On-policy vs Off-policy

🔻 Target policy

$R_{t+1} + \gamma Q(S_{t+1}, A_{t+1})$

$R_{t+1} + \gamma \max_a Q(S_{t+1}, a)$

• $Q^\pi \rightarrow q^\pi:$ Q-value를 추정하기 위해서 action을 결정하기 위해 사용하는 policy
• Sarsa: $\mu$
• Q-learning: $\pi$

🔻 Behavior policy

• Sample data를 수집하기 위해 모델이 실제로 행동하는 policy.
• Sarsa, Q-learning 모두 현재 policy $\pi$에 따라 행동한다.

🔷 On-policy

• target policy = behavior policy
• 모델이 실제로 행동한 data를 반영하여 업데이트를 진행한다.
• Stochasitic policy를 사용한다고 볼 수 있다.
• Current policy를 통해 얻은 sample data를 사용하기 때문에, policy가 업데이트할 때 해당 sample data만 고려한다.
• Sub-optimal policy이다.

🔷 Off-policy

• target policy ≠ behavior policy
• 모델이 실제로 행동한 방식과 무관하게 최적의 action에 따라 업데이트를 진행한다.
• Deterministic policy를 사용한다고 볼 수 있다.
• $\max_a Q(S_{t+1}, a)$를 통해 업데이트를 진행하기 때문에, 지금까지 추정한 모든 $Q(S_{t+1}, A_{t+1})$를 고려한다.
• 수집한 sample data를 따르지 않기 때문에 조금 더 exploration을 한다고 볼 수 있다.

---

4️⃣ 정리

🔷 12강에서 배운 내용은 아래와 같다.

1. Temporal Difference Learnings에 대해서 배웠다.
2. TD의 종류의 Sarsa와 Q-learning에 대해 배웠다.
3. Sarsa와 Q-learning의 pseudo code를 살펴보았다.
4. On-policy와 Off-policy에 대해 살펴보았다.