👨‍🏫학습목표

오늘은 Importance Sampling과 Off-policy Monte Carlo and Temporal Difference에 대해 배워볼 예정이다.

👨‍🎓강의영상: https://www.youtube.com/watch?v=1BcEwmxSr8E&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=14

1️⃣ Importance Sampling

🔷 Importance Sampling 등장배경

• 앞서 우리는 On-policy와 Off-policy에 대해 배웠다.
• 그런데 On-policy보다는 Off-policy가 장점이 더 많이 때문에 우리는 Monte Carlo와 Sarsa를 On-policy에서 Off-policy로 바꾸려고 한다.
• 구체적으로 각 방식의 behavior policy를 다른 것으로 바꾸는 방법을 통해 이를 구현한다.
• 이때 사용되는 개념이 Importance Sampling이다.

$\mathbb{E}[f] = \int f(x) p(x) dx = \int f(x) \frac{p(x)}{q(x)} q(x) dx$

• 실제로 적분을 계산하는 대신 sampling을 통해 기대값을 구할 수 있다.

$\approx \frac{1}{N} \sum_n \frac{p(x_n)}{q(x_n)} f(x_n) \text{ where } x_n \sim q(x)$

• 이를 Monte Carlo sampling이라고 한다.
• sampling을 통해 근사값을 구할 수 있다.
• 그런데 $x \sim p(x)$일때, $p(x)$에서 $x$를 sampling하는 것이 어려울 수 있다.
• 예를 들어 $p(x)$가 복잡한 함수일 경우 sampling하는 것이 어려울 수 있다.

그래서 우리는 $p(x)$대신 우리가 잘 알고 있는 Uniform 혹은 Gaussian 분포에서 sampling을 할 계획이다.

하지만 $p(x)$와 $q(x)$는 다른 함수이기 때문에 오차가 발생한다. 이를 보정하기 위해서 $\frac {p(x_n)}{q(x_n)}$를 곱한다.

이를 Importance weight라고 한다. 그리고 이러한 방식을 통해 기대값을 구하는 것을 Importance Sampling이라고 한다.

🔻 Discrete한 경우

$\mathbb{E}_{X \sim P}[f(X)] = \sum P(X) f(X) = \sum Q(X) \frac{P(X)}{Q(X)} f(X)$

$= \mathbb{E}_{X \sim Q}[\frac{P(X)}{Q(X)} f(X)]$

🔻 Continuous한 경우

$\mathbb{E}[f] = \int f(x) p(x) dx = \int f(x) \frac{p(x)}{q(x)} q(x) dx$

$\approx \frac{1}{N} \sum_n \frac{p(x_n)}{q(x_n)} f(x_n) \text{ where } x_n \sim q(x)$

🔷 Monte Carlo에 적용하기

$q_\pi(s, a) = \mathbb{E}_\pi[G_t | S_t = s, A_t = a]$

$G_t = R_{t+1} + \gamma R_{t+2} + \dots + \gamma^{T-t-1} R_T$

• 우리는 궁극적으로 Policy $\pi$를 따르는 Return $G_t$의 기대값 $\mathbb{E}_\pi[G_t | S_t = s, A_t = a]$를 구하고 싶다.
• 이때 $G_t$는 sample data $S_t, A_t, R_{t+1}, S_{t+1}, \dots, R_T, S_T$ 를 통해 구할 수 있다.
• 그리고 기대값을 구하기 위해서는 확률 $P(A_t, S_{t+1}, A_{t+1}, \dots, S_T | S_t, A_{t:T-1} \sim \pi)$를 알아야 한다.

그리고 해당 확률은 아래와 같이 표현할 수 있다.

$P(A_t, S_{t+1}, A_{t+1}, \dots, S_T | S_t, A_{t:T-1} \sim \pi) = \prod_{k=t}^{T-1} \pi(A_k | S_k) p(S_{k+1} | S_k, A_k)$

앞서 배운 내용과 연결해보면

$\mathbb{E}[f] = \mathbb{E}_\pi[G_t | S_t = s, A_t = a]$

$p(x) = \prod_{k=t}^{T-1} \pi(A_k | S_k) p(S_{k+1} | S_k, A_k)$

• 우리는 원칙적으로 Policy $\pi$를 따르는 $p(x)$를 통해 계산을 해야 하지만 behavior policy $\mu$를 따르는 $q(x)$를 통해 $\mathbb{E}[f]$를 구할 수 있다.

Importance weight는 아래와 같이 설계할 수 있다.

$\rho_t^T = \frac{\prod_{k=t}^{T-1} \pi(A_k | S_k) p(S_{k+1} | S_k, A_k)}{\prod_{k=t}^{T-1} \mu(A_k | S_k) p(S_{k+1} | S_k, A_k)} = \prod_{k=t}^{T-1} \frac{\pi(A_k | S_k)}{\mu(A_k | S_k)}$

• 이때 $p(S_{k+1} | S_k, A_k)$가 약분이 되어 transition probability를 모르더라도 연산 가능하다.

---

2️⃣ Off-policy Monte Carlo and Temporal Difference

• 우리는 policy $\pi$대신에 $\mu$를 사용하여 sample을 수집 후 업데이트를 진행할 수 있다.
• 이러한 방식을 통해 우리는 Monte Carlo와 Temporal Difference를 Off-policy로 전환할 수 있다.

🔷 Off-policy Monte Carlo

$G_t^{\pi/\mu} = \rho_t^T G_t = \left(\prod_{k=t}^{T-1} \frac{\pi(A_k | S_k)}{\mu(A_k | S_k)}\right) G_t \quad (\mu > 0 \text{ if } \pi > 0)$

$= \mathbb{E}_\mu[G_t^{\pi/\mu} | S_t = s, A_t = a]$

• $\frac{\pi(A_k | S_k)}{\mu(A_k | S_k)}$ 는 stochastic한데 $\Pi$를 통해 곱해지기 때문에 variance가 크게 증가한다.
• variance가 커지면 학습과정에서 convergence가 느려진다.

🔷 Off-policy Temporal Difference

$Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \frac{\pi(A_k | S_k)}{\mu(A_k | S_k)} [R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t)]$

• $\frac{\pi(A_k | S_k)}{\mu(A_k | S_k)}$ 는 stochastic하기 때문에 variance가 증가한다.
• Monte Carlo보다는 variance가 작기 때문에 convergence가 빠르다.

---

3️⃣ Bias vs Variance

우리는 계속해서 $q_\pi(s, a)$를 추정하려 하고 있다.

🔷 Bias

• 우리가 추정한 추정치의 평균값과 실제 값이 얼마나 떨어져 있는지를 의미한다.

🔷 Variance

• 우리가 추정한 추정치의 흩어진 정도를 의미한다.

출처: https://scott.fortmann-roe.com/docs/BiasVariance.html

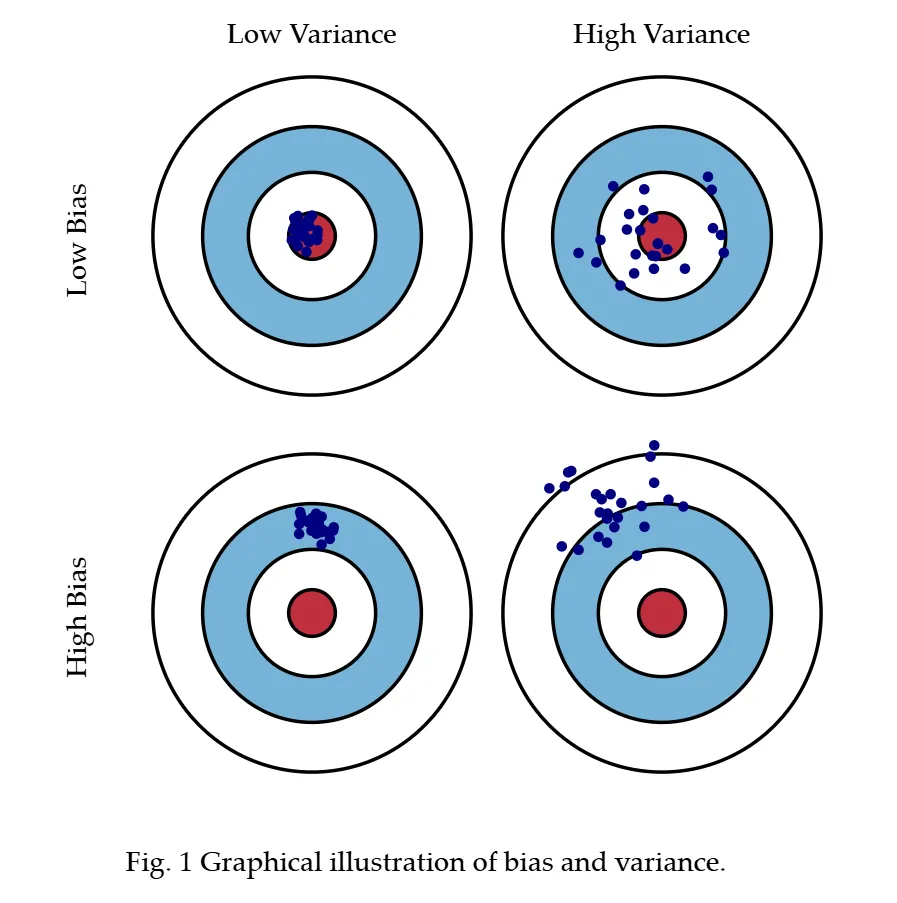
🔷 Bias and Variance in MC and TD

🔻 Monte Carlo

• Return $G_t$를 target으로 한다.

• Return $G_t$는 $q_\pi(s, a)$의 unbiased estimate이기 때문에 Monte Carlo는 bias가 없다.

• $G_t$를 추정할 때 Random성이 높은 성질이 있다.

• Temporal Difference보다 Variance가 크다.

🔻 Temporal Difference

• $R_{t+1} + \gamma Q_\pi(S_{t+1}, A_{t+1})$를 target으로 한다.

• $R_{t+1} + \gamma Q_\pi(S_{t+1}, A_{t+1})$는 $R_{t+1} + \gamma q_\pi(S_{t+1}, A_{t+1})$의 근사치이다.

• 따라서 $R_{t+1} + \gamma q_\pi(S_{t+1}, A_{t+1})$는 $q_\pi(s, a)$의 biased estimate이다.

• 업데이트를 진행할 때 Random한 성질이 반영된다.

---

4️⃣ Monte Carlo VS Temporal Difference

종류	Monte Carlo	Temporal Difference
Sampe data	episode	next state
memory and computation	high	low
evironment	끝이 있는 episode에 적용 가능	끝이 없는 episode에도 적용 가능
Markov property	Markov property가 적어도 성능 저하가 적다.	Markov property가 성능에 큰 영향을 끼친다.
초기값	민감하지 않다.	민감하다
Convergence 속도	느리다	빠르다
특징	이해하기 쉽다. 직관적이다.	효율적이다.

---

5️⃣ 정리

🔷 14강에서 배운 내용은 아래와 같다.

1. Importance Sampling의 개념에 대해 배웠다.
2. Monte Carlo sampling에 대해 배웠다.
3. Off-policy를 적용한 Monte Carlo와 Temporal Difference에 대해 살펴보았다.
4. Monte Carlo와 Temporal Difference를 Bias와 Variance 관점에서 살펴보았다.