👨‍🏫학습목표

오늘은 Distributional RL의 개념과 한계에 대해 배워볼 예정이다.

👨‍🎓강의영상: https://www.youtube.com/watch?v=VYWdspLnhDE&t=784s

1️⃣ Distributional Reinforcement Learning

🔷 Distributional RL

• 지금까지 다뤘던 모델은 데이터를 수집할 때 state, action를 구하는 과정에서 각각 random성이 반영되었다.
• 이러한 모델은 reward는 특성한 실수값으로 다루었다.
• Distributional RL은 Reward로 random variable을 사용하여 random성을 부여하였다.

$Z^\pi(x, a) = \sum_{t\geq0} \gamma^t R(x_t, a_t). \\ Q(x, a) = \mathbb{E}[R(x, a) + \gamma Q(X',A')]$

• Return 역시 Random variable의 합이라 확률 분포로 표현될 수 있다.
• 이를 Random Return이라 한다.
• Return에 expectation을 추가하여 Q-value로 만들 수 있다.

$Z^\pi(x, a) = \sum_{t\geq0} \gamma^t R(x_t, a_t).$

• 우리는 Random Return $Z^\pi(x, a)$ 을 사용하며, action-value distribution이라 부른다.

🔻 Distributional Bellman equation

• Action-value distribution에 대한 식이다.
• 지금부터는 Distribution 간의 관계를 이용하여 policy를 다룬다.

🔷 Distributional Bellman equation으로 이해

🔻 Policy Evaluation

$Z(x, a) \stackrel{D}{=} R(x, a) + \gamma Z(X',A')$

• 주어진 policy에서 위 식을 만족하는 policy를 찾는 것이 목적이다.
• Distributional RL에서는 state를 $x$로 표현한다.
• 우리는 모든 state, action에서 위 식을 만족하는 policy를 찾는 것이 목적이다.

$Z \leftarrow \mathcal{T}^\pi Z$

• $\mathcal{T}:$ Distributional Bellman operator
• Bellman operator를 통해 업데이트된 policy를 찾는다.
• 위 과정을 Iteration 과정을 통해 하나의 $Z$로 converge한다.

🔻 Control (Policy Improvement)

• Distributional Bellman optimal equation을 사용한다.
• Distributional Bellman optimality operator $\mathcal{T}$ 를 사용한다.
• Contraction이 없어서 distributional instability 문제가 발생한다.
• 또한 Converge된다는 보장이 없다.
• Improvement 역시 보장되지 않는다.

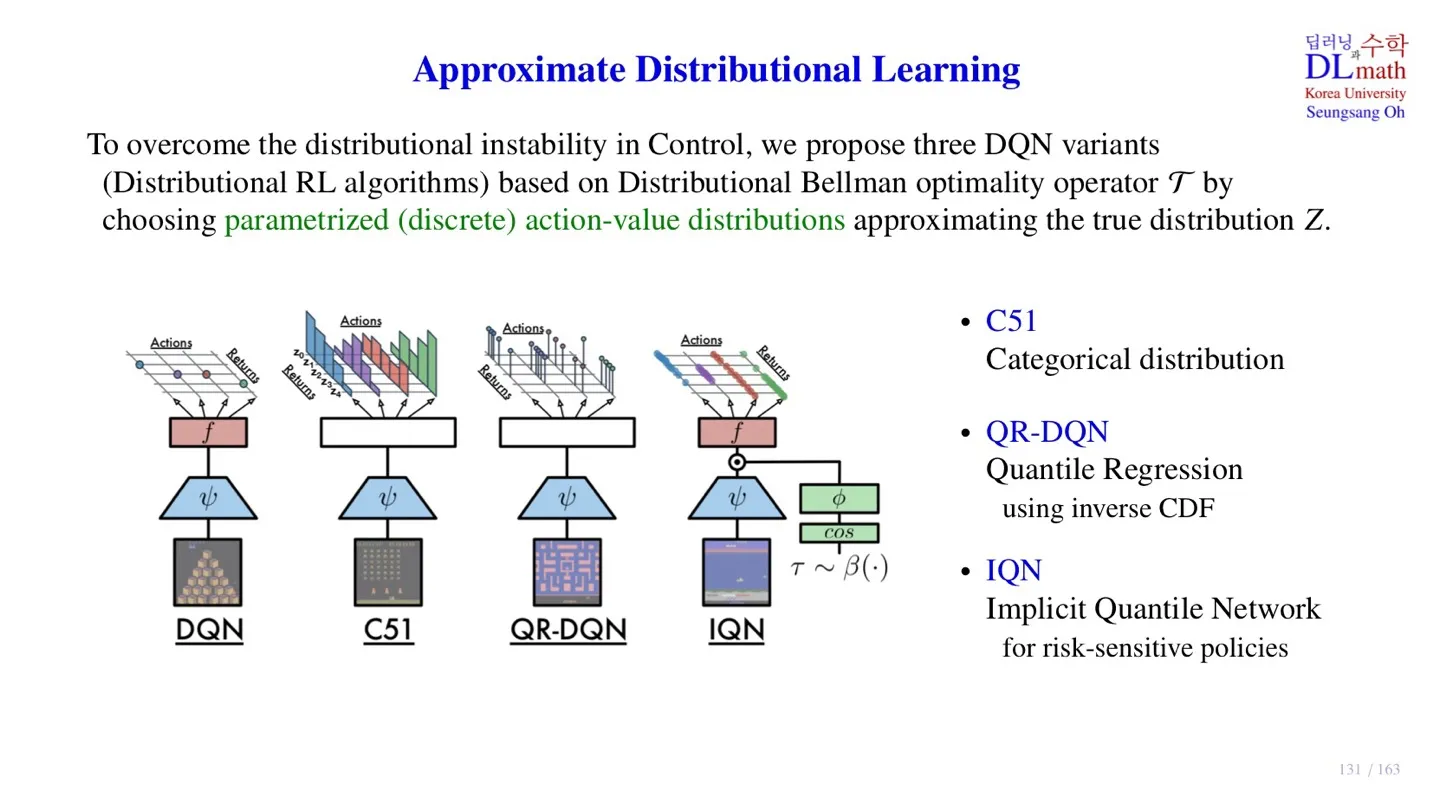
🔻 Approximate Distributional learning

• 위 과정이 practical하게 적용하기 어렵기 때문에 discrete action-value distribution을 사용한다.
• 이를 DQN에 적용한 것이 C51, QR-DQN, IQN이다.

---

2️⃣ Distribution을 사용하는 이유

🔷 Conventional RL

출처: https://www.researchgate.net/figure/The-decomposition-of-multimodal-distribution_fig2_371345550

• 기존의 모델들은 Bellman equation에 따라 return의 기대값을 사용한다.
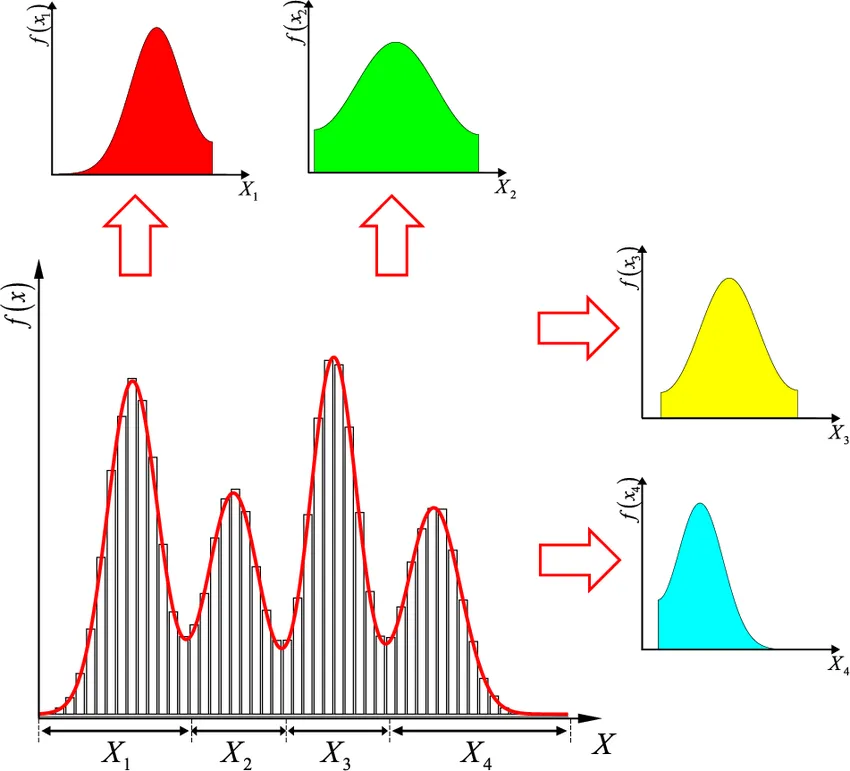
• 이때 사용하는 Return이 stochastic하여 multimodal distribution을 따를 수 있다.
• Distribution에서 극대값을 mode라고 하는데, mode가 2개 이상인 분포를 multimodal distribution이라 한다.
• 그렇다면 expectation을 사용하는 것은 optimal이 아닌 sub-optimal한 값에 도달할 수 있다.

🔷 예시를 통한 문제점 이해

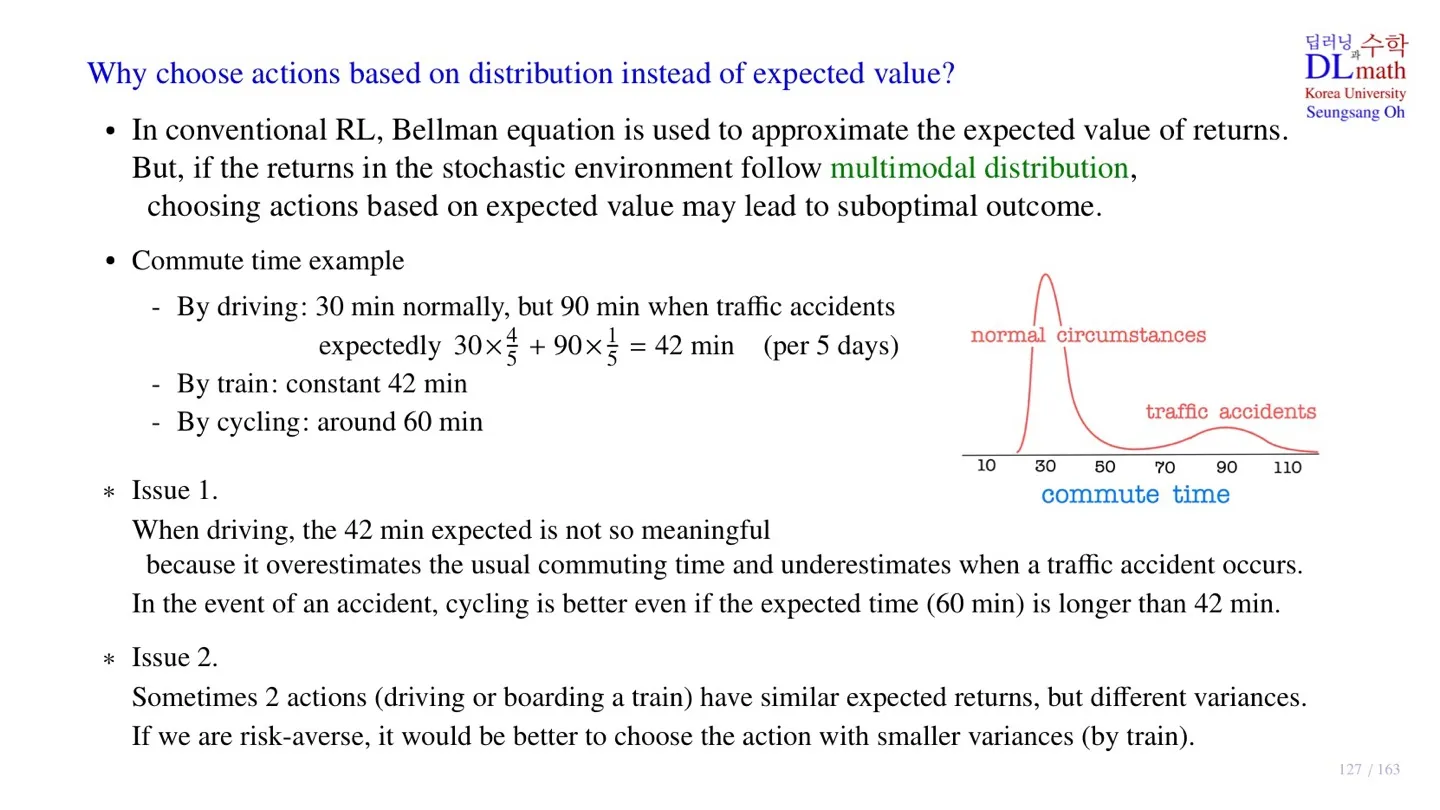
🔻 Issue 1

• 예시에 나타난 운전자의 운전시간은 30분이거나 90분이다.
• 따라서 운전시간에 대한 기대값 42분은 유의미한 정보를 제공하지 않는다.

🔻 Issue 2

• 운전과 기차 모두 expectation이 같다.
• 하지만 두 값의 분산이 다르기 때문에 risk한 상황을 피하고 싶다면 기차를 선택하는 것이 더 안전한다.
• Expectation을 통해서는 이러한 상황을 알 수 없지만, distribution을 사용하면 이러한 정보도 알 수 있다.

따라서 우리는 Action을 선택할 때, distribution을 사용하는 것이 더 좋을 수 있다.

---

3️⃣ p-Wasserstein metric

🔷 Metric의 조건

🔻 Distance

1. $d(P, Q) \geq 0:$ 거리 개념이기 때문에 0 이상이어야 한다.
2. $d(P, Q) = 0 \iff P \stackrel{D}{=} Q :$ 확률분포 $P$와 $Q$가 almost everywhere 같아야 한다.

🔻 Symmetric

1. $d(P, Q) = d(Q, P):$ P에서 Q까지의 거리와 Q에서 P까지의 거리가 같다.

🔻 Triangular inequality

1. $d(P, Q) \leq d(P, R) + d(R, Q)$

🔷 Divergence

• Metric의 2번째 조건을 만족하지 않는다.

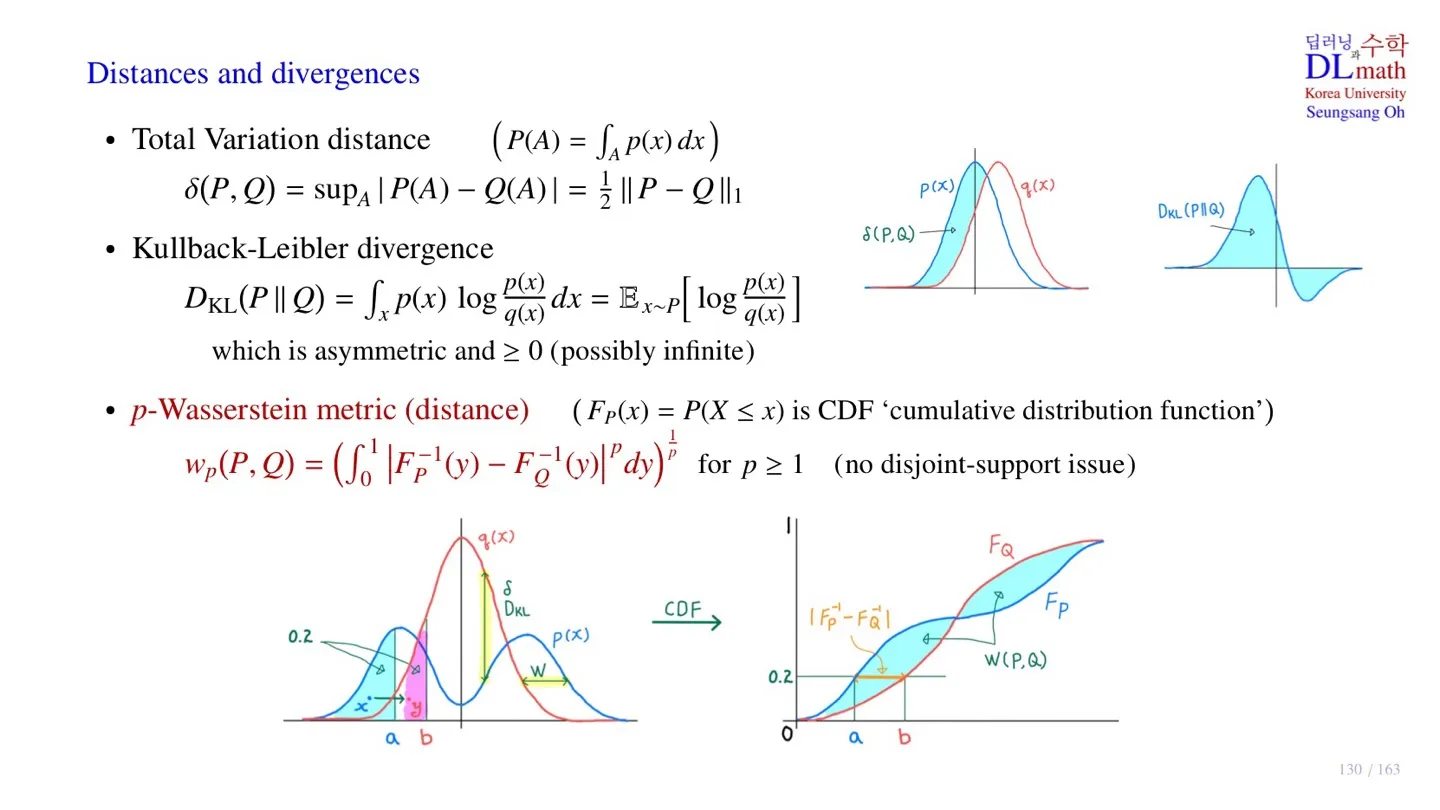
🔷 p-Wasserstein metric

🔻 등장하게 된 배경

• 현재 distribution $Q_1$과 $Q_2$는 $P$와 멀리 떨어져 있다.
• 이때는 $Q_1$과 $Q_2$ 의 Total Variation distance와 Kullback-Leibler divergence가 크게 차이나지 않는다.
• Distribution $Q$를 $P$로 학습시키려고 할 때, 우리는 $Q_2$에서 $Q_1$으로 이동할 때 metric이 줄어들길 바란다.
• 그래서 stribution $Q$를 $P$로 이동시키기 위해 설계된 metric이 Wasserstein metric이다.

🔻 핵심 아이디어

$w_p(P, Q) = \left(\int_0^1 |F_P^{-1}(y) - F_Q^{-1}(y)|^p dy\right)^\frac{1}{p} \text{ for } p \geq 1$

• 각 확률분포의 분위수 값이 같아지도록 distrance를 설계한다.
• 각 분위수가 동일한 면적을 차지하기 때문에 누적분포의 x값 거리가 줄어들도록 하는 것이다.
• CDF 사이의 거리를 모두 합하면 면접이 되고, 우리는 이 면적의 크기가 줄어드는 방향으로 학습을 수행할 수 있다.

🔻 Wasserstein metric의 장점

1. 분포가 너무 멀어서 Total Variation distance가 변하지 않는 문제를 해결할 수 있다.
2. Kullback-Leibler divergence에서 분모에 0이 들어가는 문제를 해결할 수 있다.

---

4️⃣ Wasserstein metric

🔷 Distributional Bellman equation

$Z(x, a) \stackrel{D}{=} R(x, a) + \gamma Z(X',A')$

• 확률 분포를 사용하여 관계를 나타내며, expectation을 사용하지 않는다.

🔷 Policy Evaluation

• 모든 state, action 데이터에 대하여 distributional Bellman equation을 만족하는 $Z^\pi$를 찾는 것이 목적이다.

🔻 Distributional Bellman operator

$(\mathcal{T}^\pi Z)(x, a) \stackrel{D}{=} R(x, a) + \gamma Z(X',A') \quad \Longrightarrow \quad Z^\pi = \mathcal{T}^\pi Z^\pi$

• 위 과정을 operator를 사용하면 편리하게 수행할 수 있다.
• 위 operator에 state와 action을 대입한 것은 Random reward와 주어진 policy에서 next state $X'$, next action $A'$에 대한 Return의 합을 구한 것이다.

🔻 Policy Evaluation

• Policy $\pi$가 주어졌을 때, 해당 policy의 operator $\mathcal{T}^\pi$ 가 Wasserstein metric의 maximual form 안에서 contraction이 된다.

$\bar{w}_p(Z_1, Z_2) = \sup_{x, a} w_p(Z_1(x, a), Z_2(x, a))$

• $Z_1(x, a), Z_2(x, a)$ 는 state, action이 들어오면 어떤 distribution이 된다. 즉 확률분포가 된다.
• 우리는 두 분포 사이에 Wasserstein metric을 정의할 수 있다.
• 이를 통해 우리는 모든 state, action에 대하여 두 확률분포의 거리를 구할 수 있다.
• 우리는 이 distance의 상한을 구할 수 있다.
• $\bar{w}_p(Z_1, Z_2) \leq \delta :$ 두 확률분포 사이의 Wasserstein metric을 제한할 수 있다.

$Z_{k+1} := \mathcal{T}^\pi Z_k$

• operator를 적용하여 업데이트 된 Return을 구할 수 있다.

$\mathcal{T}^\pi: Z \rightarrow Z \text{ is a } \gamma\text{-contraction in } \bar{w}_p,$

$\text{ meaning } \bar{w}_p(\mathcal{T}^\pi Z_1, \mathcal{T}^\pi Z_2) \leq \gamma \bar{w}_p(Z_1, Z_2) \text{ for } Z_1, Z_2 \in \mathcal{Z}.$

• $\gamma = 0.9$ 라면 operator를 적용할 경우, 기존의 distance의 0.9배보다 더 작아졌다.

$\bar{w}_p(Z_{k+1}, Z_k) = \bar{w}_p(\mathcal{T}^\pi Z_k, \mathcal{T}^\pi Z_{k-1}) \leq \gamma \bar{w}_p(Z_k, Z_{k-1})$

$\text{ and so } \{Z_k\} \text{ converges to } Z^\pi \text{ in } \bar{w}_p.$

• 해당 과정을 반복하여 converge 할 수 있다.
• 따라서 operator를 통해 Distributional Bellman equation을 만족하면서, Wasserstein metric을 통해 converge를 이끌어낼 수 있다.

---

5️⃣ Control

🔷 Distributional Bellman optimality equation

$Z^*(x, a) \stackrel{D}{=} R(x, a) + \gamma Z^*(X', \arg \max_{a'} \mathbb{E}[Z^*(X', a')])$

• Return $Z^*(x, a)$은 distribution으로 바뀐다.
• Reward $R(x, a)$ 역시 distribution으로 바뀐다.

🔷 Distributional Bellman optimality operator

$(\mathcal{T}Z)(x, a) \stackrel{D}{=} R(x, a) + \gamma Z(X', \arg \max_{a'} \mathbb{E}[Z(X', a')])$

• Optimality 역시 operator를 정의할 수 있다.
• Optimal한 연산은 특정 policy를 다루지 않기 때문에 $\pi$를 사용하지는 않는다.

🔷 Control

• Control에서는 optimal policy를 찾는 것이 목적이다.
• Operator를 통해 $Z^*$를 구할 수 있고, $Z^*$의 expectation을 통해 $Q$를 구할 수 있다.
• 우리는 $Q$를 maximize하는 action을 선택하는 optimal policy를 구할 수 있다.
• 이를 위해서는 operator가 contraction이 되어야 한다.

🔻 Distributional Bellman optimality operator의 문제점

• Contraction하지 않는다.
• 이를 distributional instability라고 한다.
• 어떤 metric을 사용하여도 continuous하지 않다.
• 또한 많은 optimal action-value distribution이 존재한다.
• 다만 optimal policy가 unique하다면policy로 이때는 optimal converge한다.

이러한 다양한 문제를 극복하기 위해 Approximate Distributional Learning을 사용한다.

---

6️⃣ Approximate Distributional Learning

🔷 Distributional Reinforcement Learning

• Policy evaluation 단계에서 Wasserstein metric을 사용해야 한다.
• Control 단계에서 distributional instability가 발생한다.

🔷 DQN

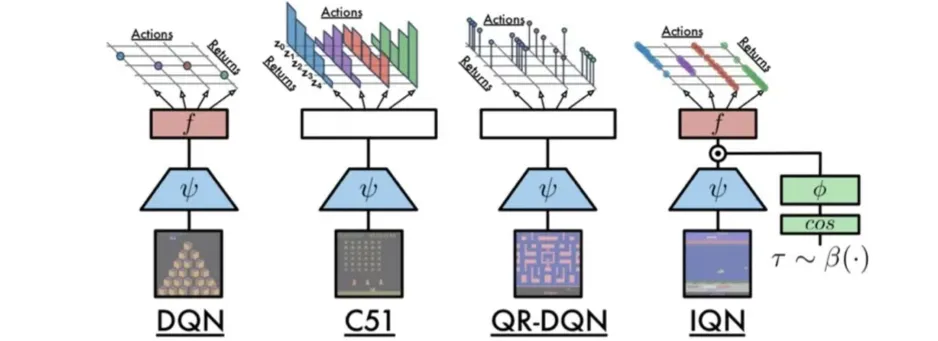
• 기존의 DQN은 입력으로 state를, 출력으로 Q-value를 반환한다.
• Q-Network를 사용한다.
• 이때 Action의 개수가 finite하다

🔷 DQN 변형

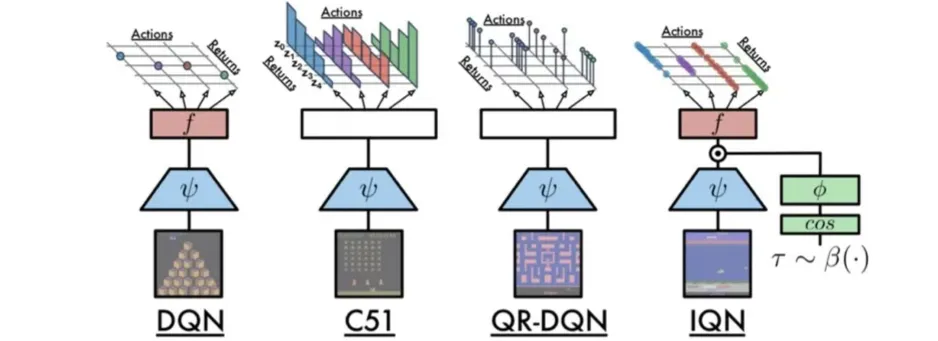
• 각 Action별로 distribution $Z(x, a_i)$이 표현된다.
• 하지만 continuous한 distribution을 출력하기 어렵기 때문에 discrete action-value distribution을 출력한다.

---

7️⃣ 정리

🔷 31강에서 배운 내용은 아래와 같다.

1. Distribution으로 reward를 다루면 더 많은 정보를 활용할 수 있다.
2. Distribution으로 데이터를 처리할 경우 contraction하기 힘들다는 한계가 존재한다.
3. 기존 DQN을 변형하여 distribution을 출력할 수 있도록 설계한다.