👨‍🏫학습목표

오늘은 IQN에 대해 배워볼 예정이다.

👨‍🎓강의영상: https://www.youtube.com/watch?v=RihBHbp9dBA&t=2123s

IQN 논문: https://arxiv.org/pdf/1806.06923

1️⃣ IQN

📕 지난 시간에 배운 내용

• Distribution Bellman equation을 통해 학습을 할 때 많은 metric에서 contraction이 되지 않는다는 한계가 존재한다.

• Wasserstein metric을 통해 contraction을 확보할 수 있다.

• 하지만 Wasserstein metric은 SGD가 적용되지 않기 때문에 적용하기 어렵다는 한계가 존재한다.

• 또한 DQN은 continuous한 출력을 반환할 수 없다는 한계가 존재한다.

• C51과 QR-DQN, IQN 모두 discrete distribution을 반환함으로써 이러한 한계를 극복한다.

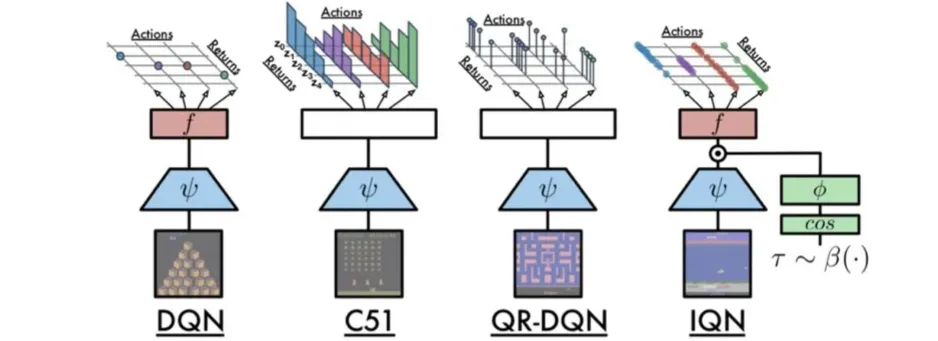
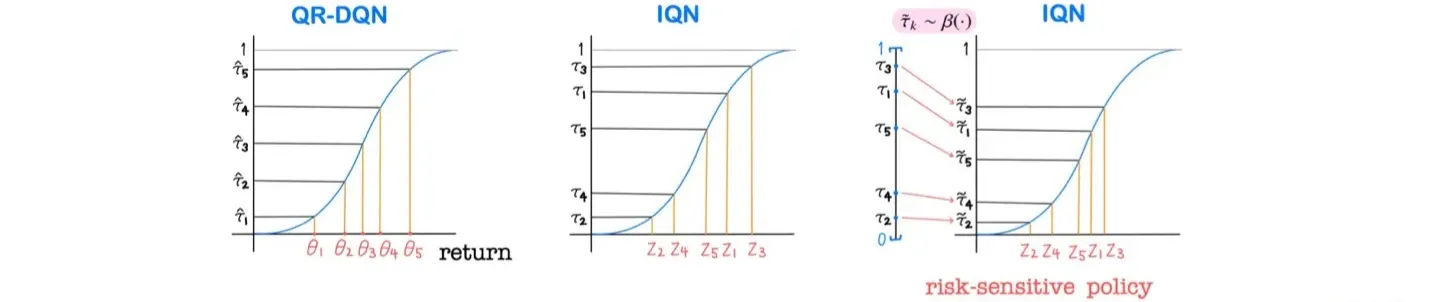
🔷 Implicit Quantile Network

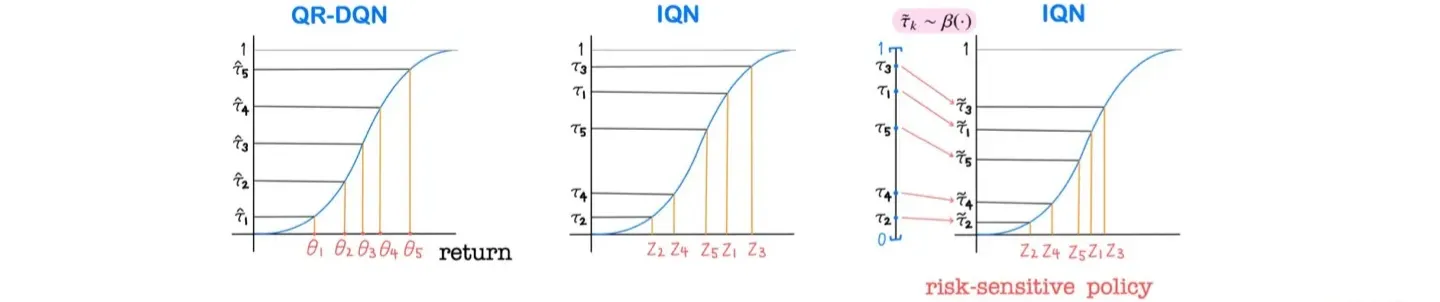
• QR-DQN의 Implicit 버전의 모델이다.

• Target distribution을 예측하기 위한 quantile point를 sampling을 통해 결정한다.

• Sampling을 하기 때문에 Quantile의 개수 $N$에 영향을 받지 않는다.

• Approximation error는 신경망의 크기나 학습 데이터의 크기에 영향을 받는다.

• 또한 $\beta$를 이용하여 특정한 종류의 policy를 만들 수 있다.

---

2️⃣ Risk-Sensitive Reinforcement Learning

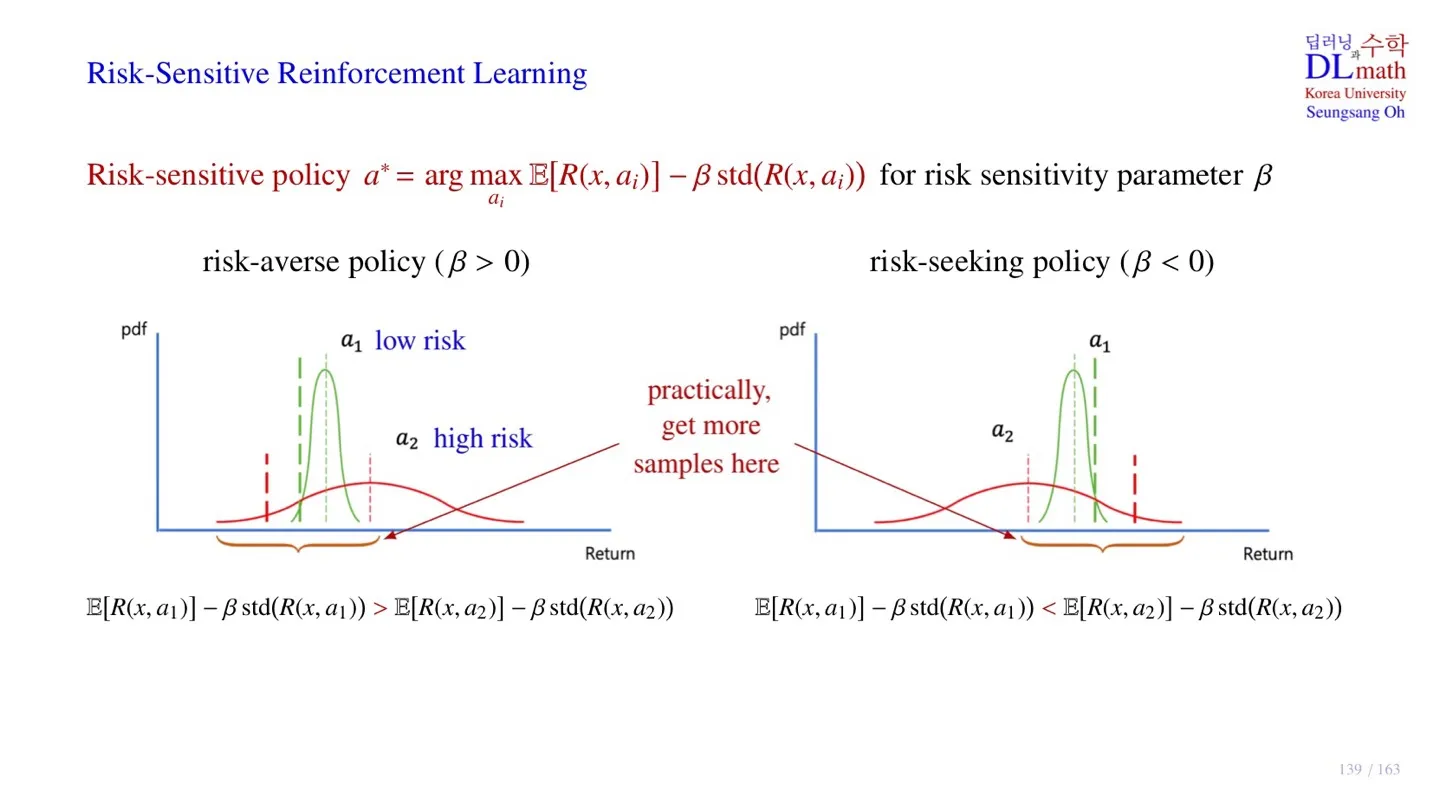
🔷 Greedy policy

$a^* = \arg \max_{a'} Q(s,a')$

• 지금까지 우리는 최적의 action을 선택하는 Greedy policy를 사용하였다.

🔷 Risk-sensitive policy

• Low risk에서는 Return값의 variance가 작다.
• High risk에서는 Return값의 variance가 크다.

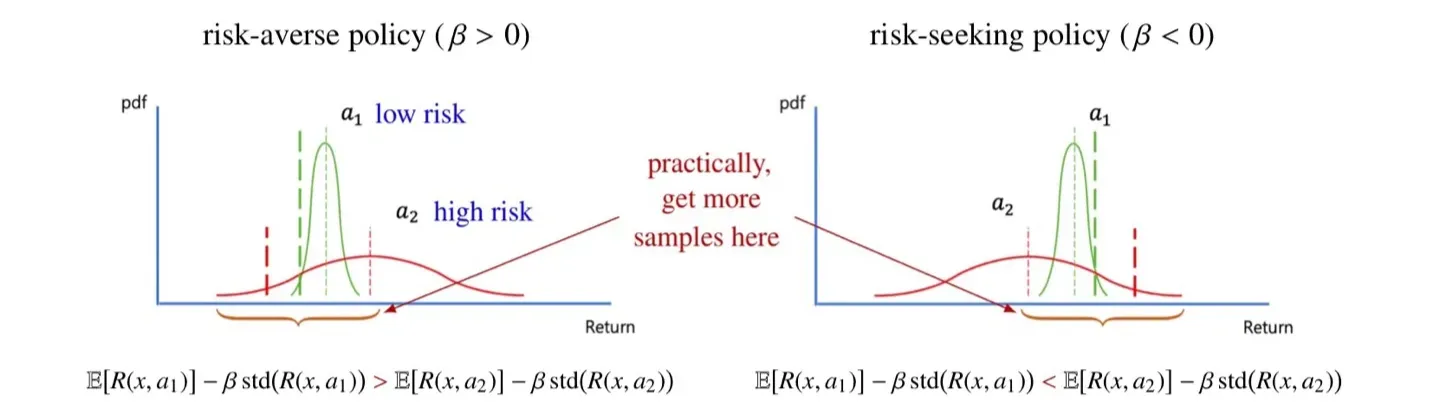
🔻 Risk-averse policy $(\beta > 0)$

$\mathbb{E}[R(x, a_1)] < \mathbb{E}[R(x, a_2)]$

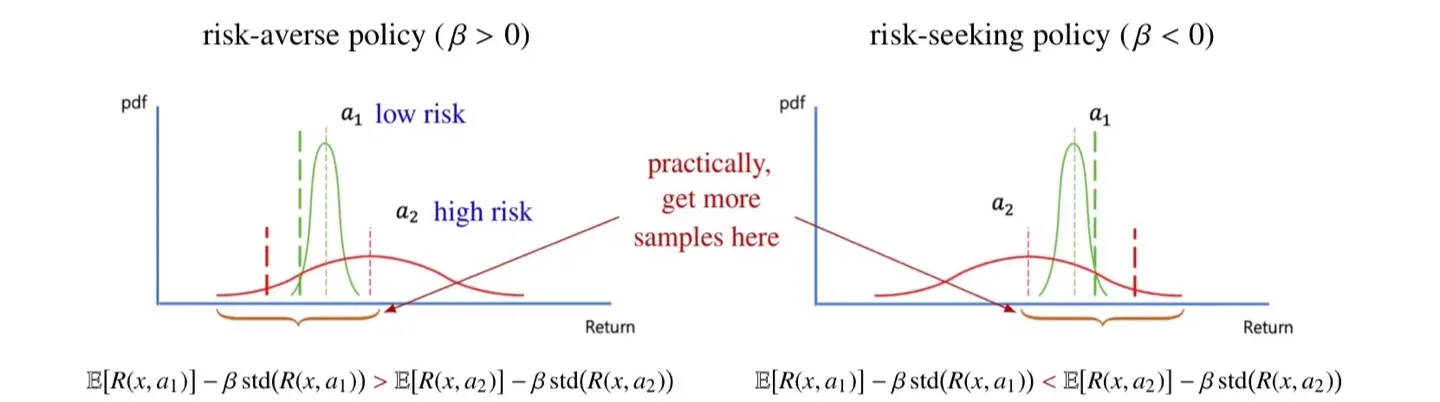
• Expectation만 비교했을 때는 $a_2$가 그 값이 더 크다.

$\mathbb{E}[R(x, a_1)] - \beta \text{std}(R(x, a_1) > \mathbb{E}[R(x, a_2)] - \beta \text{std}(R(x, a_2)$

• 하지만 Standard error를 뺄 경우 $a_1$값의 크기가 더 크다.

$a^* = \arg \max_{a_i} \mathbb{E}[R(x, a_i)] - \beta \text{std}(R(x, a_i))$

• 따라서 해당 식을 사용하면 평균적인 return값은 작지만 variance가 작은 $a_1$이 next action으로 선택된다.

🔻 Risk-seeking policy $(\beta < 0)$

$\mathbb{E}[R(x, a_1)] > \mathbb{E}[R(x, a_2)]$

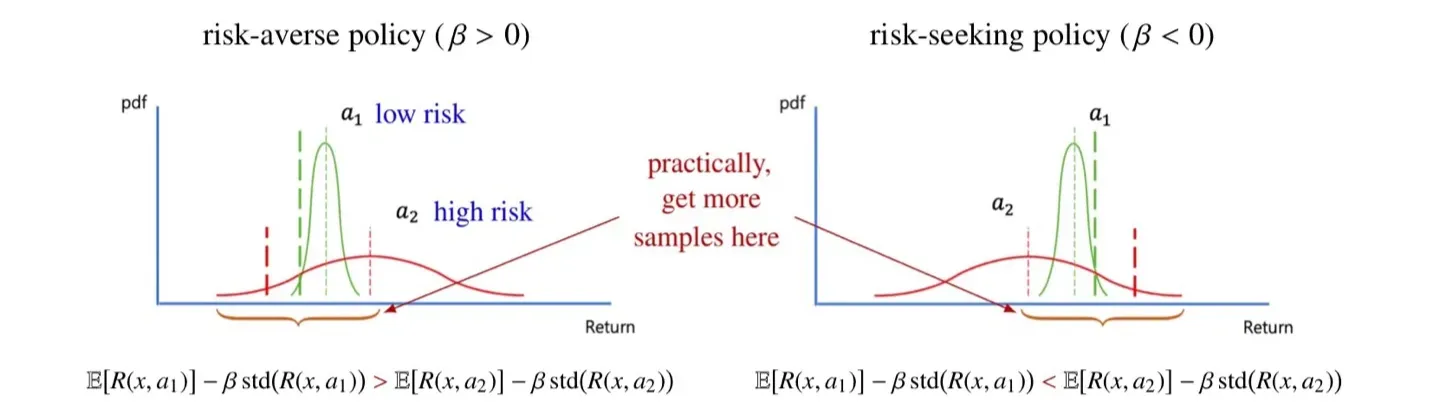
• Expectation만 비교했을 때는 $a_1$가 그 값이 더 크다.

$\mathbb{E}[R(x, a_1)] - \beta \text{std}(R(x, a_1) < \mathbb{E}[R(x, a_2)] - \beta \text{std}(R(x, a_2)$

• 하지만 Standard error를 뺄 경우 $a_2$값의 크기가 더 크다.

$a^* = \arg \max_{a_i} \mathbb{E}[R(x, a_i)] - \beta \text{std}(R(x, a_i))$

• 따라서 해당 식을 사용하면 평균적인 return값은 작지만 variance가 큰은 $a_2$이 next action으로 선택된다.
• $a_2$는 평균적인 return은 작지만 운이 좋으면 더 큰 return을 얻을 수도 있다.

🔻 Practical algorithm

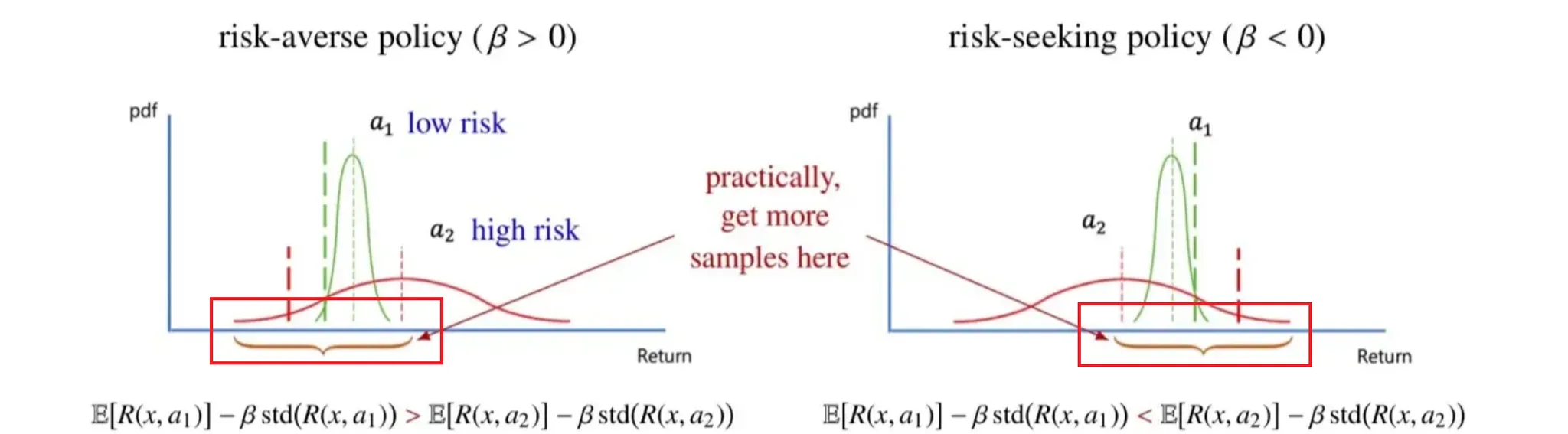
• 강화학습에서는 실제로 standard error를 빼지 않고, 해당 영역만에서 sampling을 하는 방식으로 구현한다.

---

3️⃣ Distortion risk measure

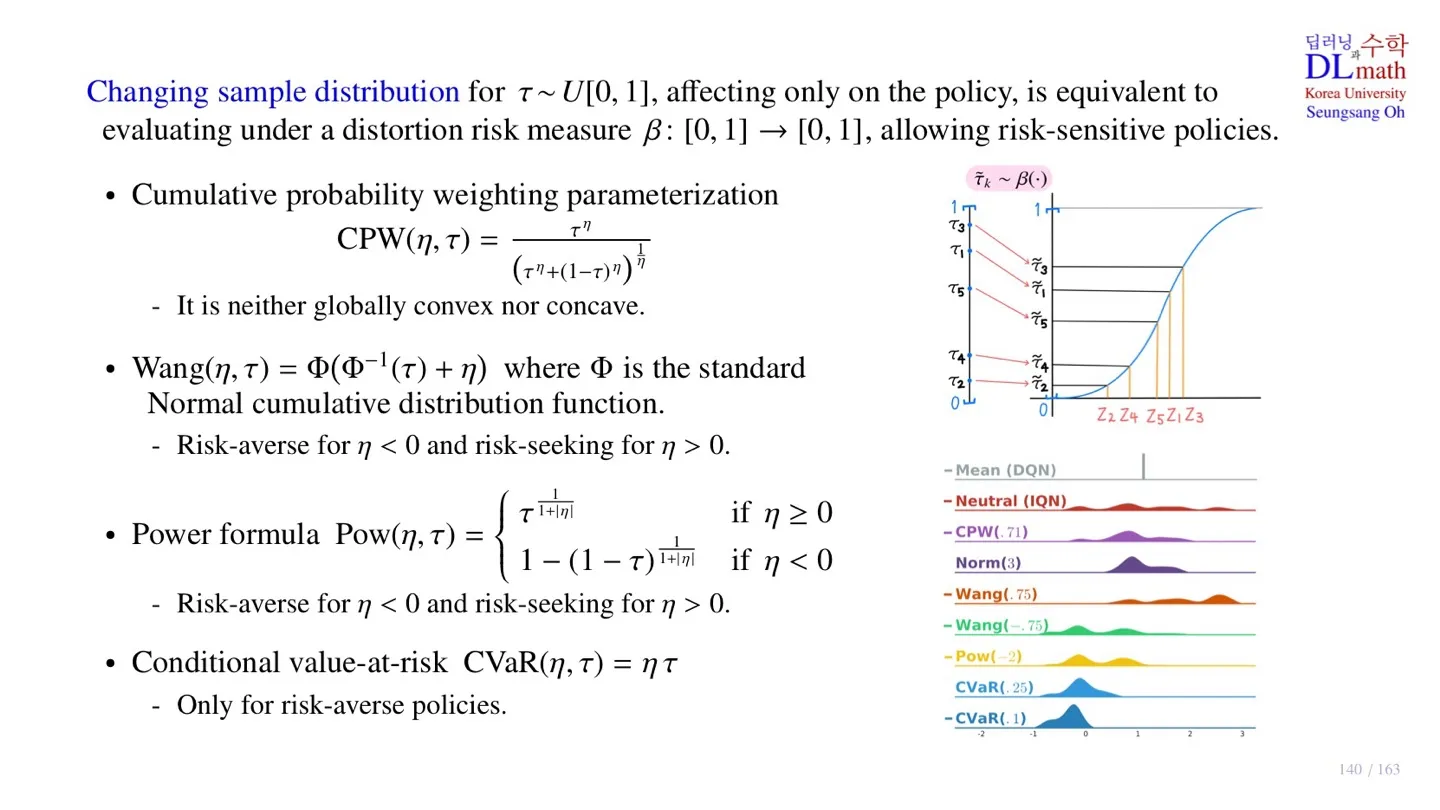
🔷 Distortion risk measure

• $\beta: [0,1] \rightarrow [0,1]$
• 특정 영역에서 Sampling을 할 수 있도록 $\tau$값을 조정한다.

🔷 Cumulative probability weighting parameterization

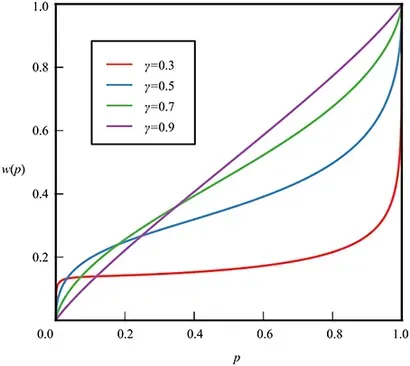
출처: https://www.frontiersin.org/journals/psychology/articles/10.3389/fpsyg.2016.00778/full

$\text{CPW}(\eta, \tau) = \frac{\tau^\eta}{(\tau^\eta + (1-\tau)^\eta)^{\frac{1}{\eta}}}$

• $\eta:$ 얼마나 왜곡할지 결정하는 하이퍼파라미터
• Quantile value $\tau$가 입력되면 위 식을 통해 변형한다.

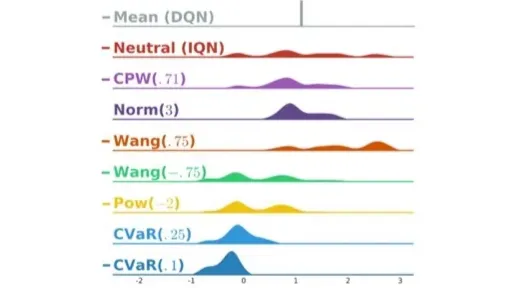
• 현재 Return의 expectation이 1로 되어 있다.

• Neutral IQN은 distortion risk measure를 사용하지 않고 sampling한 것이다.

• CPW는 $\eta = 0.71$로 Return값이 조금 더 가운데로 몰려있는 형태이다.

• 다른 분포도 마찬가지로 각자 만의 식을 통해 분포를 변형한다.

---

4️⃣ IQN의 Implementation

🔷 IQN의 데이터 처리

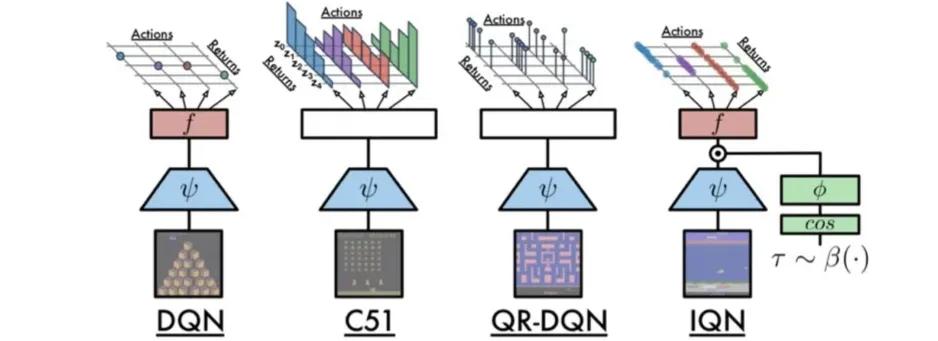
• IQN은 quantile function $Z_{\tau}$를 학습한다.
• IQN은 입력으로 state 외에도 quantile value를 받는다.
• 각 action에 대해 해당 quantile의 return 값 하나만 출력된다.

🔷IQN의 구조

$Z_\tau(x, a) \approx f(\psi(x) \odot \phi(\tau))_a$

• $\psi(x):$ DQN에서 살펴본 CNN을 의미한다.
• $f(x):$ Fully-connected Network를 의미한다.
• $\phi(\tau):$ Quantile 정보를 추가로 입력받는다.

🔸 DQN 구조

$\phi: [0, 1] \to \mathbb{R}^d \text{ by } \phi_j(\tau) := \text{ReLU}\left(\sum_{i=0}^{n-1} \cos(\pi i \tau)w_{ij} + b_j\right) \ \text{with} \ n=64$

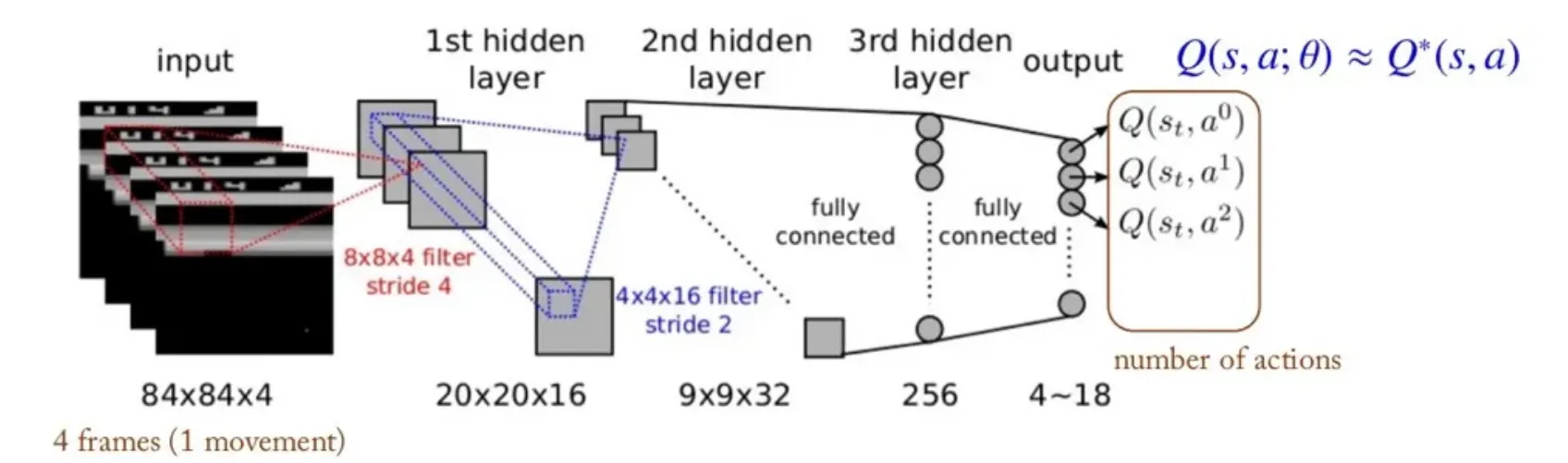
• $\phi(\tau)$는 위와 같이 정의하였다.

🔷 IQN의 pseudo code

• Random return을 사용할 때, quantile을 위한 sampling의 개수를 모두 다르게 설계할 것을 확인할 수 있다.
• Distortion risk measure $\beta$는 greedy policy를 수행할 때만 사용한다.

---

5️⃣ 정리

🔷 34강에서 배운 내용은 아래와 같다.

1. IQN은 학습하는 분포를 변형하여 학습하는 분포의 risk 정도를 조정한다.
2. 기존 모델과 달리 Quantile value를 입력으로 받는다.