👨‍🏫학습목표

오늘은 C51의 한계를 극복한 QR-DQN에 대해 배워볼 예정이다.

👨‍🎓강의영상: https://www.youtube.com/watch?v=NZP7Va21WO8

QR-DQN 논문: https://arxiv.org/pdf/1710.10044

1️⃣ QR-DQN

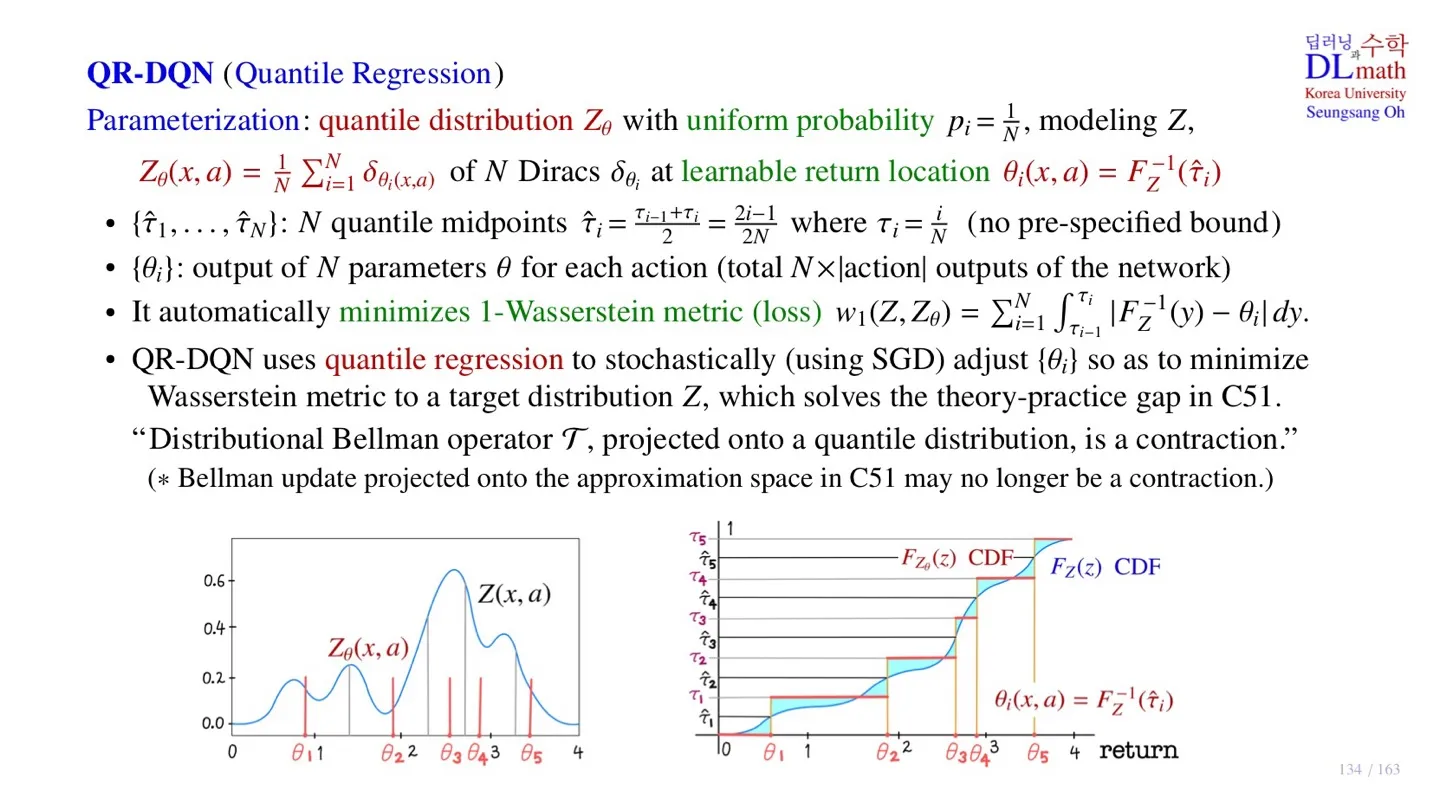
📕 지난 시간에 배운 내용

🔻 Distributional Reinforcement Learning

• Distributional Reingorcement Learning은 Reward를 Random variable로 처리한다.
  
  

$Z^\pi(x, a) = \sum_{t\geq0} \gamma^t R(x_t, a_t)$

• Action-value distribution을 사용한다.
  
  

$Z(x, a) \stackrel{D}{=} R(x, a) + \gamma Z(X',A')$

• Distributional Bellman equation을 사용한다.

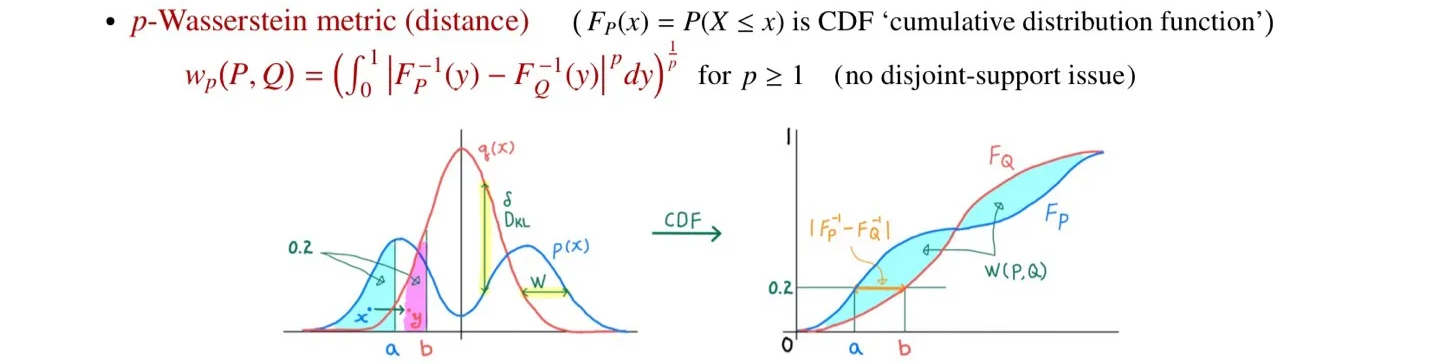
• Contraction을 이끌어내기 위해 Wasserstein metric를 사용하였다.
• Distribution을 출력하기 위해 Discrete Distribution으로 변환하였다.

Distributional Reinforcement Learning에 대한 추가적인 내용은 아래 글에서 확인 가능하다.

📃자료: https://velog.io/@tina1975/Deep-Reinforcement-Learning-31강-Distributional-Reinforcement-Learning

🔷QR-DQN vs C51

🔻 C51

• Discrete distribution으로 변환한다.

• Return의 범위를 $[ R_{min}, R_{max}]$로 제한한다.

• 균등한 간격으로 $N$개로 나눠 fixed support $\{z_1, \dots,z_N\}$를 정의한다.

• Dirac function $\delta_{z_i}$을 사용하여 Return값을 고정한다.

• 학습 가능한 확률 $p_i(x, a)$를 통해 distribution을 학습한다.
  
  

C51에 대한 추가적인 내용은 아래 글에서 확인 가능하다.

📃자료: https://velog.io/@tina1975/Deep-Reinforcement-Learning-32강-C51

🔻 QR-DQN

• 확률을 fix하고 support를 learnable하게 바꿔준다.
• 확률을 $p_i = \frac{1}{N}$로 고정한다.

$\theta_i(x, a) = F_Z^{-1}(\hat{\tau}_i)$

$Z_0(x, a) = \frac{1}{N} \sum_{i=1}^N \delta_{\theta_i(x, a)}$

• 파라미터 $\theta_i$는 quantile regression을 사용하여 support값을 학습한다.

🔷 Quantile regression

• 확률 $p_i(x, a)$가 $\frac{1}{N}$로 고정되어 있으므로 support 지점이 확률 분포를 잘 대표해야 한다.
• Support 지점이 좌우로 각각 $\frac{1}{2N}$ 영역의 중앙에 위치하여 해당 분포를 표현하도록 학습한다.

$\{\hat{\tau}_1, \dots, \hat{\tau}_N\}$

$\hat{\tau}_i = \frac{\tau_{i-1} + \tau_i}{2} = \frac{2i-1}{2N}$

• $\tau_i$가 있을 때, 이 값의 중앙값을 사용한다.
• $\hat\tau_i$을 quantile midpoint라고 한다.

🔷 QR-DQN의 출력

• 모델이 구하고자 하는 값은 Random Return $Z(x, a)$값이다.

$Z_0(x, a) = \frac{1}{N} \sum_{i=1}^N \delta_{\theta_i(x, a)}$

• 이를 위해 우리는 Return의 location을 학습한다.

🔷 QR-DQN의 학습

$w_1(Z, Z_\theta) = \sum_{i=1}^N \int_{\tau_{i-1}}^{\tau_i} |F_Z^{-1}(y) - \theta_i| dy$

• $Z:$ Target distribution
• $Z_{\theta}:$ Quantile distribution
• Target distribution을 사용하여 Quantile distribution을 학습한다.
• Target distribution $Z$와 Quantile distribution $Z_{\theta}$의 Wasserstein metric이 최소가 되도록 학습한다.

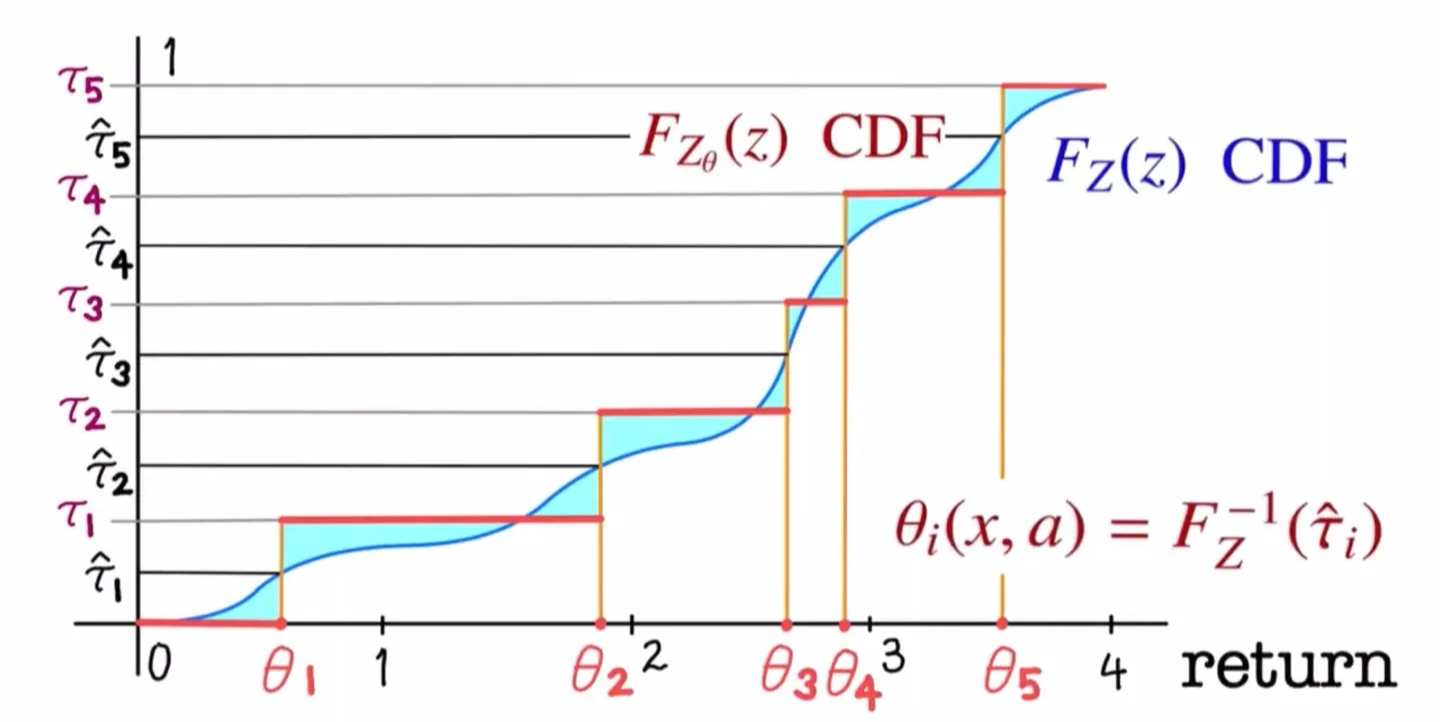
• Wasserstein metric은 두 분포의 CDF의 차이 면적이 최소화되도록 학습한다.
• 현재 자료의 파란 영역을 최소화되도록 학습한다.
• $\theta$를 quantile midpoint $\hat\tau_i$에 해당하는 지점에 뒀을 때 면적이 최소화된다.

🔻 Quantile regression의 장점

• Quantile regression을 사용하면 SGD를 사용할 수 있다.

• Quantile regression을 사용하면 CDF의 inverse를 구하면 되기 때문에 Wasserstein metric을 직접 계산할 필요가 없다.

• 하지만 Wasserstein metric을 충족한 값을 구할 수 있다.

---

2️⃣ Quantile Regression

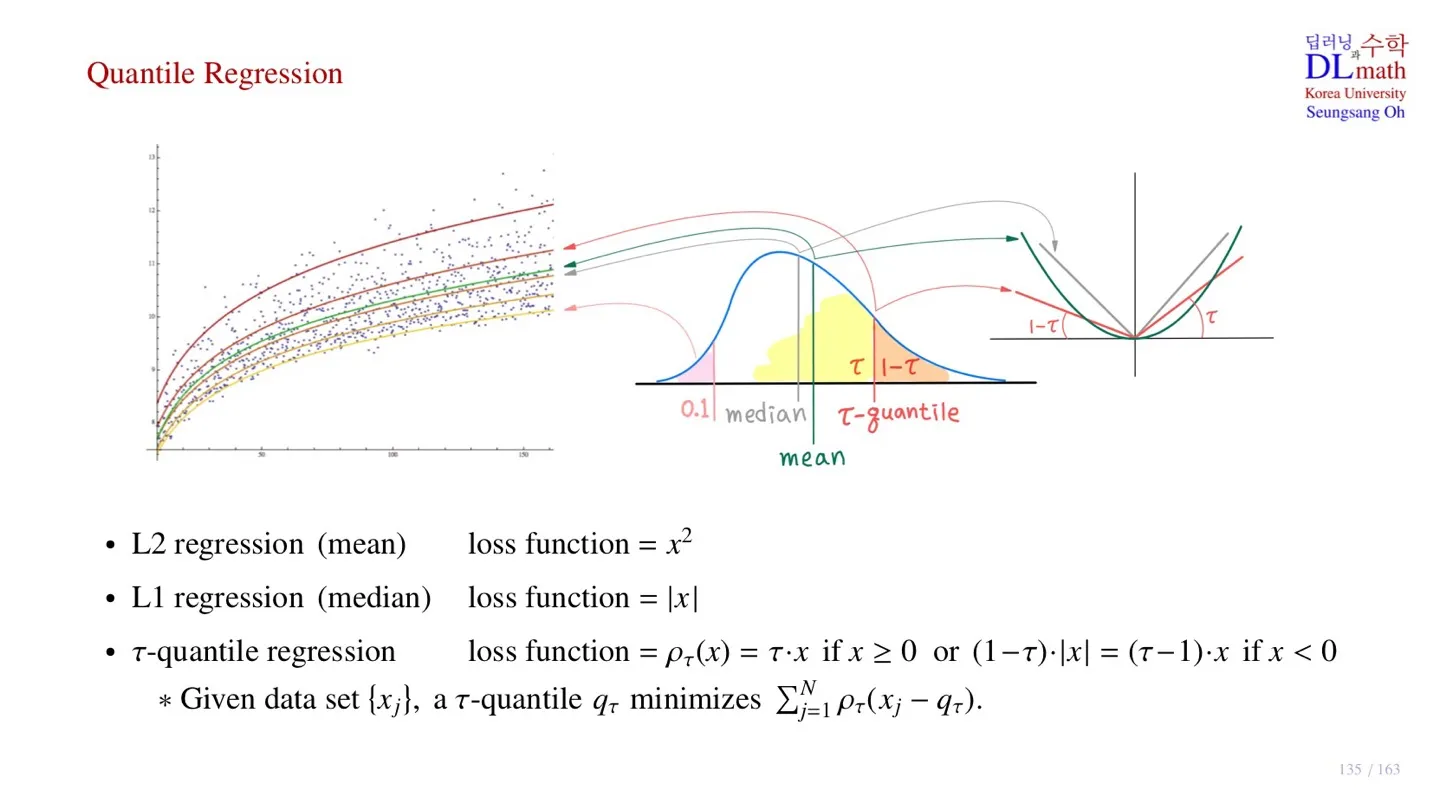
🔻 Linear regression

• MSE를 loss function으로 사용하여 W와 b를 구한다.
  
  

🔻 L2 regression

• $x^2$을 loss function으로 사용한다.
• 평균을 학습한다.
  
  

🔻 L1 regression

• $|x|$을 loss function으로 사용한다.
• 중위수를 학습한다.
  
  

🔻 $\tau$-quantile regression

• 해당 분위수를 지나가도록 학습한다.

🔸 Loss function

$\rho_\tau(x) = \tau x \text{ if } x \geq 0 \text{ or } (1-\tau)|x| = (\tau-1)x \text{ if } x < 0$

$\text{ minimizes } \sum_{j=1}^N \rho_\tau(x_j - q_\tau)$

• 한쪽 영역은 $\tau$만큼, 다른 쪽 영역은 $1-\tau$ 만큼 데이터가 분포하도록 한다.

🔸 예시

---

3️⃣ Quantile Regression Loss

🔷 Quantile regression loss

$\sum_{i=1}^N \mathbb{E}_j[\rho_{\hat{\tau}_i}(\mathcal{T}\theta_j - \theta_i(x, a))] = \frac{1}{N} \sum_{i=1}^N \sum_{j=1}^N \rho_{\hat{\tau}_i}(\mathcal{T}\theta_j - \theta_i(x, a))$

• $N$개의 파라미터를 출력한다.
• $\mathcal{T}\theta_j:$ Target
• $\theta_i(x, a):$ Behavior
• Quantile Regression을 사용한다.

$\mathcal{T} \theta_j \leftarrow r + \gamma \theta_j(x', a^*) \text{ for } a^* = \arg \max_a Q(x', a)$

• Next state와 next action을 Bellman equation에 넣어 Target값을 구한다.

⭐ 중요 포인트!

Quantile regression loss를 최소화시키는 파라미터 $\theta_i$가 Wasserstein loss $w_1(Z, Z_\theta)$를 최소화시킨다.

Quantile regression loss는 Stochastic gradient descent를 사용할 수 있다.

🔻 계산 예시

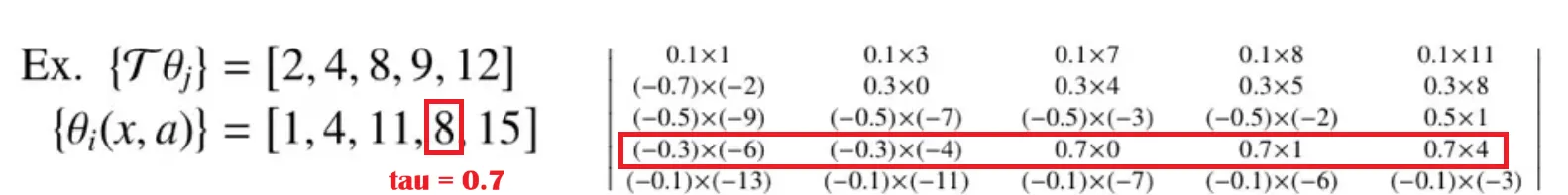
🔷 Quantile Huber Loss

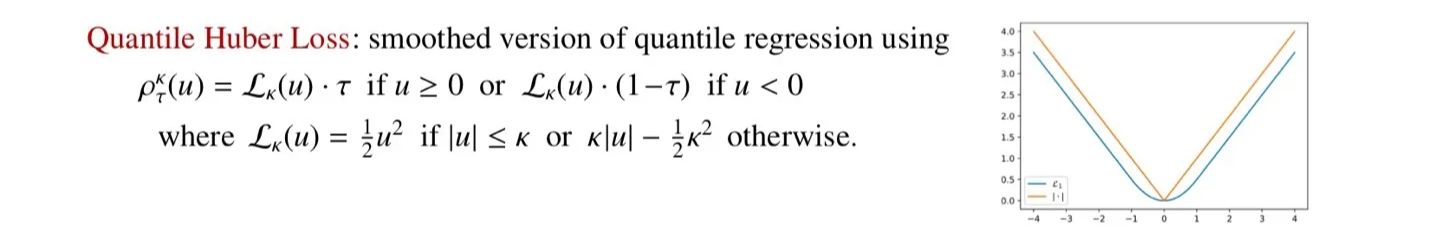
• Quantile regression loss는 미분 불가능한 지점이 있다.
• 이를 해결하기 위해 Quantile Huber Loss를 사용하여 함수를 smooth하게 만든다.

🔻 구체적인 수식

$\rho_\tau^\kappa(u) = \mathcal{L}_\kappa(u) \cdot \tau \text{ if } u \geq 0 \text{ or } \mathcal{L}_\kappa(u) \cdot (1-\tau) \text{ if } u < 0$

$\text{where } \mathcal{L}_\kappa(u) = \frac{1}{2}u^2 \text{ if } |u| \leq \kappa \text{ or } \kappa|u| - \frac{1}{2}\kappa^2 \text{ otherwise.}$

---

4️⃣ QR-DQN의 이점

🔻 C51의 한계

• C51은 Return의 범위 $[ R_{min}, R_{max}]$를 지정해야 한다.

• 하지만 이 과정은 쉽지 않다.

• C51에서는 support를 일치시키기 위한 projection 과정을 거쳐야 한다.

• C51에서는 KL-발산을 통해 학습하기 때문에 Wasserstein metric이 최소화된다는 보장이 없다.

🔻 QR-DQN의 이점

• QR-DQN은 Return의 범위를 미리 지정할 필요가 없다.

• QR-DQN은 support disjoint 문제가 발생하지 않아, projection 과정이 필요하지 않다.

• QR-DQN quantile regression을 통해 Wasserstein metric을 최소화시킬 수 있다.

🔷 QR-DQN의 pseudo code

$Q(x_{t+1}, a) = \frac{1}{N} \sum_i \theta_i(x_{t+1}, a)$

• 신경망을 통해 추출한 Return값을 통해 Q-value값을 구한다.
• Q-value값을 통해 next action을 구한다.

$\mathcal{T} \theta_j \leftarrow r_{t+1} + \gamma \theta_j(x_{t+1}, a^*)$

• Bellman update를 통해 target값을 계산한다.

$\sum_{i=1}^N \mathbb{E}_j[\rho_{\hat{\tau}_i}^\kappa(\mathcal{T} \theta_j - \theta_i(x, a))]$

• Quantile Huber Loss를 Minimize하는 방향으로 $\theta_i$를 학습한다.

---

5️⃣ 정리

🔷 33강에서 배운 내용은 아래와 같다.

1. QR-DQN은 확률을 고정하고, Return 위치를 학습한다.
2. 학습을 위해 Wasserstein metric을 사용한다.
3. Wasserstein metric은 quantile midpoint $\hat\tau_i$에서 최소화된다.
4. Wasserstein metric은 quantile regression loss로 표현할 수 있다.
5. 최종 Loss는 모든 점에서 미분 가능한 Quantile Huber Loss를 사용한다.