Singular Value Decomposition : 특이값 분해
- SVD
- 고유값 분해처럼 행렬을 대각화하는 한 방법이다.
- 고유값 분해와 달리, 정방행렬이든 아니든 관계없이 m x n 행렬에 대해 적용 가능하다.
그림으로 표현하면, SVD는 m x n 크기의 행렬 A를 다음과 같이 분해하는 것을 의미한다.
<그림1>
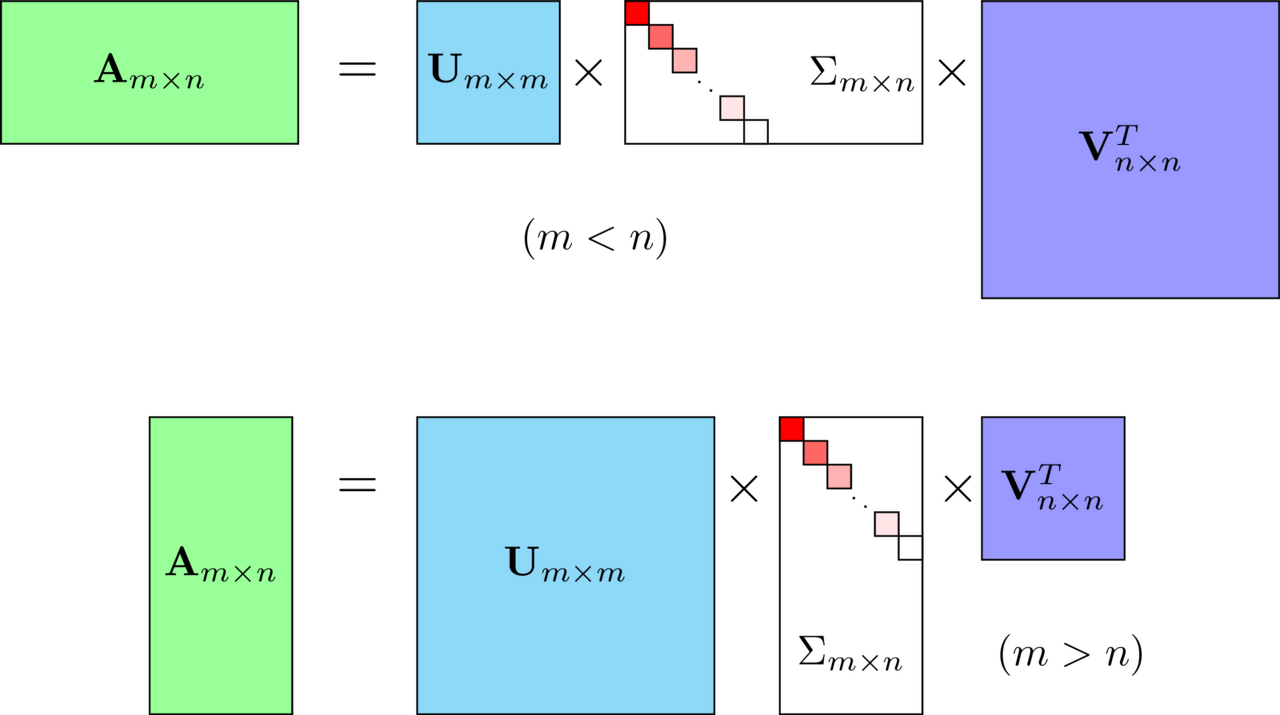
이때,
U : m x m 직교행렬
V : n x n 직교행렬
∑ : m x n 직사각 대각행렬
를 의미하며 matrix U와 V에 속한 벡터를 Singular Vector라 하고 ∑의 0이 아닌 대각 원소 값을 Singular Value라고 한다.
특히 U에 속한 벡터를 Left Singular Vector, V에 속한 벡터를 Right Singular Vector라고 한다.
위의 과정을 수식으로 표현하면
이다.
이를 이용하여
를 표현할 수 있다.
여기서 AAt, AtA 모두 대칭 행렬임을 알 수 있고, 대칭 행렬은 모두 고유값 분해가 가능하며 직교 행렬로 분해할 수 있다는 성질이 있다.
따라서 위의 수식을 통해, U는 AAt(대칭행렬)를 고유값 분해해서 얻은 직교 행렬이며, V는 AtA(대칭행렬)를 고유값 분해해서 얻은 직교 행렬이라는 것을 확인할 수 있다.
따라서 U는 AAt의 고유 벡터들로 구성된 행렬이고 마찬가지로 V는 AtA를 고유값 분해해서 얻은 행렬이다.
또한 ∑는 AtA 혹은 AAt의 고유값들에 루트를 씌어준 값으로 구성되어 있음을 확인할 수 있다.
정리하면,
SVD는 특이값 분해라고 하며, 특이값이 분해된 행렬 A는 U ∑ Vt 형태로 표현되게 된다.
행렬 U와 V에 속한 벡터를 Singular Vector라 하며 각 Singular Vector는 서로 직교하는 성질을 가진다. Singular Vector는 분해하고자 하는 matrix A의 AAt와 AtA의 고유 벡터를 계산하여 구할 수 있다.
∑는 대각행렬이며, 행렬의 대각에 위치한 값만 0이 아니고 나머지 위치의 값은 모두 0이다. ∑의 대각 원소 값이 바로 행렬 A의 Singular Value이다. A의 Singular Value은 AAt 혹은 AtA의 고유값을 계산하여 루트를 취해준 값과 같다.
- SVD의 기하학적 의미
모든 행렬은 선형 변환을 뜻하는데, 직교 행렬은 선형 변환 중 회전 변환을 의미한다. 대각 행렬은 스케일 변환을 의미한다.
아래 그림을 보며 A = U ∑ Vt에서 행렬 A의 선형 변환이 의미하는 것을 알아보겠다.
<그림2>
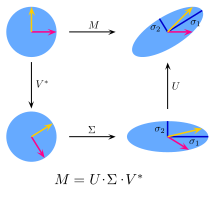
먼저 Vt로 회전 변환(Rotate)을 하고 ∑로 스케일 변환(Stretch)를 한 뒤 다시 U로 회전 변환(Rotate)을 하는 걸 볼 수 있다.
이를 좀 더 기하학적인 의미 측면에서 바라보기 위해 수식을 변경하면,
A = U ∑ Vt 에서 양변에 V를 내적하여 A V = U ∑를 유도할 수 있다.
이때, U와 V에 속한 벡터는 서로 직교하는 성질을 가진다. 따라서 서로 직교하는 벡터로 구성된 행렬 V에 선형 변환 A를 해준 뒤에도 서로 직교하는 벡터로 구성된 행렬 U가 만들어진다. 다만 그 크기가 ∑만큼 차이가 있을 뿐이다.
결론적으로 orthogonal matrix는 선형변환을 통해 크기가 다른 orthogonal matrix로 변환시킬 수 있다
Rank
임의의 행렬 A가 있을 때, 이 행렬의 Rank는 행렬의 열들로 생성될 수 있는 벡터 공간의 차원을 의미한다.
결국 차원이라고 하면 벡터 공간 상에서 기저(Basis)의 개수에 의해서 결정이 되고, 기저는 행렬의 선형 독립적인 열이 얼마나 존재하느냐에 의존한다.
열뿐만 아니라 행에서도 rank를 정의하기도 한다. A라는 행렬이 존재한다고 하면 A transpose의 rank를 구할 수 있고, 이것은 A의 Row rank를 의미한다.
여기서 중요한 사실은 Column rank(A) = Row rank(A)가 성립한다는 사실이다.
따라서 rank를 구할 때, Column과 Row를 구별하지 않고 계산 가능하다.
예를 통해서 rank에 대해서 알아보겠다.
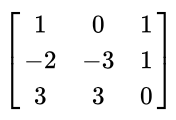
위의 행렬의 경우 rank는 2이다. 그 이유는, 첫 번째와 두 번째 열은 서로 선형 독립 관계에 있다고 볼 수 있다. 하지만, 세 번째 열의 경우에는 첫 번째 열에서 두 번째 열을 빼주게 되면 세 번째 열이 된다. 즉, 선형적으로 독립적인 열은 2개이므로 rank는 2이다.
행의 관점에서 바라보게 되면, 두 번째와 세 번째 행은 선형 독립 관계에 있다. 하지만 두 번째와 세 번째 행을 더하게 되면 첫 번째 행이 된다. 따라서 선형적으로 의존관계가 성립하고 독립적인 행은 2개가 된다. 결론적으로 열을 통해 rank를 계산했을 때와 같이, rank가 2가 된다.
위의 예를 통해 rank를 구하는 과정, Column rank와 Row rank가 일치하는 현상까지 볼 수 있었다.
결론적으로, 행렬의 rank는 행렬이 나타낼 수 있는 벡터 공간에서 기저의 개수를 의미하고, 이 기저는 서로 독립인 행 또는 열의 벡터의 개수에 의해서 결정된다. 열과 행의 rank는 서로 같은 값을 가지므로, 행렬의 rank를 구할 때에는 한쪽의 rank만 계산하면 되고 서로 선형 독립인 벡터가 몇 개가 되는지, 즉 기저가 몇 개인지 확인하면 된다.
Reference
그림1 출처 : https://www.pikpng.com/transpng/hxRRmbR/
그림2 출처 : 위키피디아 (Singular Value Decomposition)
