<인공신경망> 09. Gradient 소멸과 증폭 문제

📌 Introduction

1. Problems in deeper neural network

🔸 shallow network에 비해 neural network는 학습시키기 어려움
🔸 Neural network 학습할 때 backpropagation을 통해 gradient 값을 backward로 전파해 weight 값 업데이트
💡 backpropagation
1) feed forward로 data 넣어줌
2) 초기화된 weight 값을 통해 값 계산
3) 최종 neuron 값에 label과 함께 error(loss) 값 계산
4) error 값을 통해 gradient 계산한 값을 backward로 전파

1) Vanishing/Exploding gradient

🔸 loss function에 기반한 gradient를 backward로 전파해야함. 하지만 gradient가 backward로 layer 지날수록 사라지거나(너무 작아 0으로 수렴, Vanishing) 너무 커지는(Exploding) 일 발생 => weight 업데이트 시 업데이트된 값이 증가해 수렴하지 않음
🔸 Backward path: gradients grow smaller and smaller, or larger and larger
🔸 => lower layers: very hard to train
🔹 backpropagation에 따라 gradient 값은 backward로 갈수록 매우 작아지거나 매우 커지는데, 둘의 경우 모두 학습하기 어려움 => lower layer에서 학습이 진행되지 않으면 모든 layer가 학습되지 않음

2) Not enough training data; labelling is costly

🔸 Supervised learning의 경우 모든 data는 label을 가지고있어야함. But labelling은 시간과 노력이 많이 소요됨

3) Extremely slow training

🔸 hidden layer가 많아지게 되면 weight의 업데이트가 원활이 이루어지지 않으면서 train이 느려지게 될 수 있음

4) Risk of overfitting

🔸 model with millions of parameters
🔸 especially with not enough or too noisy training instances
🔹 parameter가 커질수록 많은 데이터가 필요한데 충분하지 않을 경우 overfitting 발생 (data보다 parameter가 많을 경우)
🔹 noisy한(정확도가 떨어지는) 데이터가 많을 경우 overfitting 발생할 가능성 있음

📌 Vanishing/Exploding Gradients Problem

1. Vanishing Gradients

🔸 output layer에서 input layer로 backward 진행할 때 backward propagation 진행하면서 gradient 값이 점점 줄어 0으로 수렴하는 현상

1) Backpropagation using gradient descent

2) Gradients often get smaller as approaching the lower layers => connection weights virtually unchanged => never converges to a good solution

🔸 weight에 gradient에 비례하는 값을 더하거나 빼서 weight 값을 업데이트하는데, gradient 값이 0이 되면 weight의 델타 값도 0이 되어 weight가 변하지 않음 => 학습이 진행되도 weight 값이 변하지 않으므로 학습 효과가 나타나지 않고 결과적으로 우리가 원하는 solution에 수렴하지 않음

2. Exploding Gradients

1) Gradients can grow bigger => insanely large weight updates => diverges

🔸 gradient 값이 커지면 weight 값이 비정상적으로 크게 업데이트 되기 때문에 이전의 weight는 현재 weight에 영향을 미치지 않게 됨. 이전까지의 학습이 영향을 미치지 않으므로 학습이 정상적으로 수행되지않음

2) mostly encountered in RNN (recurrent neural networks)

🔸 RNN에서 주로 발생 > 뒤에서 배움

3. DNNs were mostly abandoned in the early 2000s

4. Understanding of vanishing gradient(Xavier Glorot and Yoshua Bengio, 2010)

1) Sigmoid activation function: mean of 0.5, saturates at 0 or 1

🔸 이전까지는 activation function으로 sigmoid를 주로 사용
🔸 sigmoid: 평균이 0.5, 값이 얼마나 커지거나 작아지든 0 또는 1로 saturation

2) Random initialization using a normal distribution with a mean of 0 and a standard deviation of 1

🔸 학습을 진행하면서 weight 값의 초기값으로 주로 random initialization 사용. random initialization을 진행할 때 random한 값들의 분포는 normal distribution을 갖게 하고 값들의 평균은 0 , standard deviation은 1이 되는 형태 주로 사용

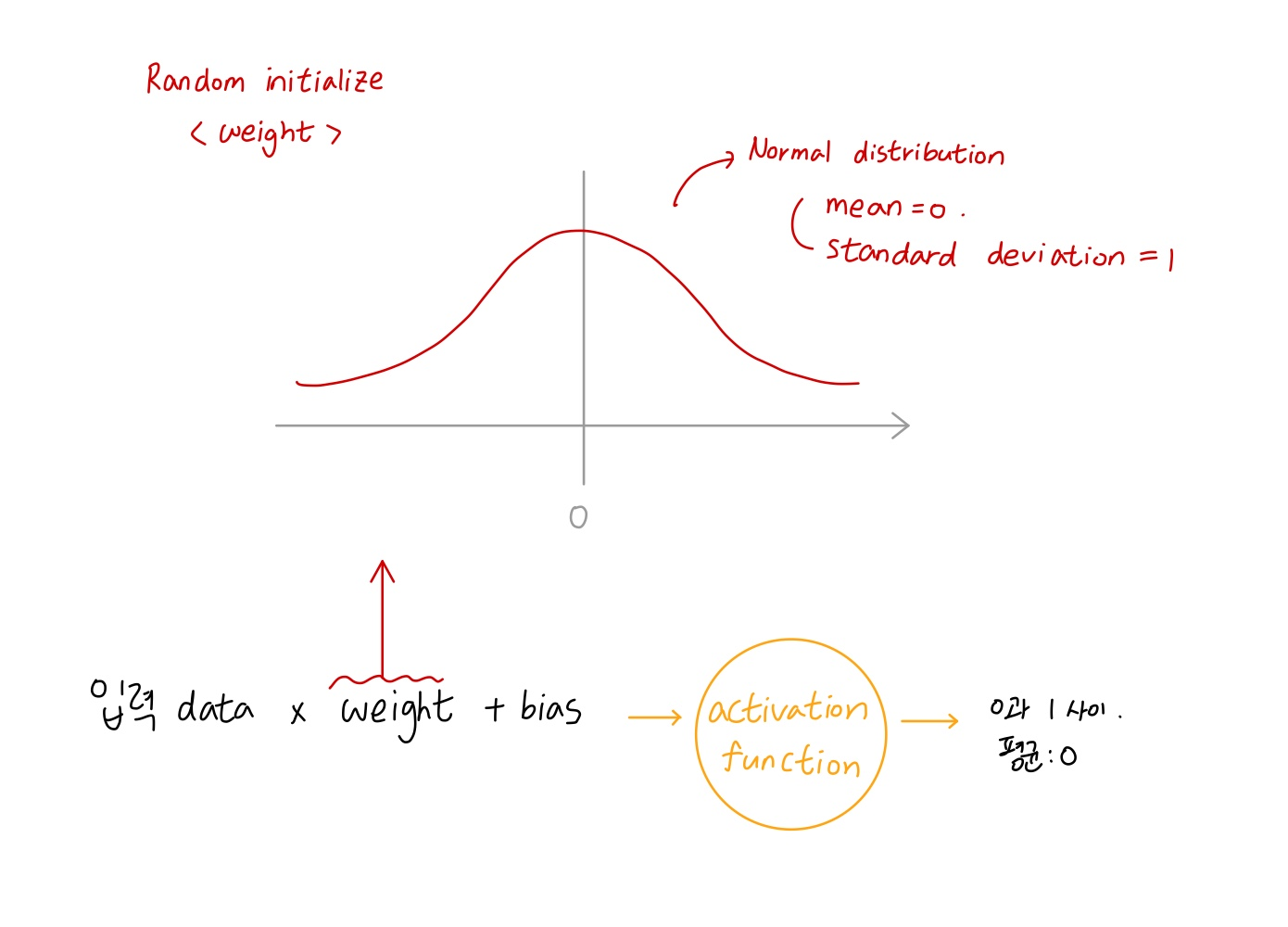
3) Variance keeps increasing => the activation function saturates at the top layers

🔸 layer 지날 때마다 값의 범위(variance) 증가 => 값이 점점 증가하거나 감소해 top layer로 갈수록 activation function이 saturate에서만 움직임
🔸 layer를 지나면서 입력 값들이 커지고 출력 값의 범위가 커짐 => 입력값이 커지면 출력값도 0~1 사이의 값을 가지고 입력값이 커지면 미분 값이 0이 되어 weight값 업데이트해도 변화가 별로 없어 학습 진행되지 않음

4) Saturation: derivative near 0 => no gradient to propagate back

🔸 saturation에서 미분하면 0에 가까움 => gradient가 0에 가까움 => weight가 변하지 않아 학습이 이루어지지 않음

📌 Xavier and He Initialization

🔸 이전까지 weight 초기화 방식이 잘못되었고, 제대로된 weight 초기화 진행해야함 => Xavier, He initialization => vanishing 문제 해결 가능

1. Proper signal flow in both directions: prediction and backpropagation => equal variances of the outputs and inputs and variances of gradients before and after flowing through a layer in the reverse direction

🔸 forward 방향과 backward 방향 양쪽으로 적절한 signal flow가 이루어져야 prediction이 이루어지고 backpropagation이 이루어져 학습 진행
🔸 equal variance: 각 layer의 input과 output의 variance(범위)가 같아야함 => layer를 지날수록 범위가 점점 커지면 안 됨
🔸 variance of gradients: 반대 방향(backward)으로 흘러갈 때 layer에 들어가고 나오는 gradient의 variance(범위)도 같아야함 (= 동일한 분포 유지)
🔸 not possible to guarantee both unless a layer has an equal number of input and output connections
🔹 input과 output connection의 크기가 같아야 위의 내용 guarantee 가능

2. Xavier initialization (or Glorot initialization)

🔸 input과 output의 connection 크기가 같은 것은 매우 어렵기 때문에 Xavier initialization 실행

1) $fan_{in}, fan_{out}$: the number of input and output connections

2) Normal distribution with mean 0 and variance, $a^2$=1/$fan_{avg}$, where $fan_{avg}=(fan_{in}+fan_{out})/2$

3) Uniform distribution between -r and r, with r=$\sqrt{3/fan_{avg}}$

🔸 해당 범위에 uniform하게 값 분포

4) Speed up training considerably

🔸 위를 통해 weight 초기화시키면 train 속도가 빨라짐
🔸 한 epoch을 train하는 시간이 빨라진 것이 아니라 학습에 필요한 epoch의 수가 줄어듬

5) One of the tricks that led to the current success of Deep Learning

3. LeCun initialization

🔸 $fan_{avg}$ -> $fan_{in}$ in the Xavier initialization

4. He initialization

🔸 $a^2$(normal) = 2/$fan_{in}$

5. 요약

Initialization	Activation functions	variance(normal)	r(uniform)
Glorot	None, tanh, logistic, softmax	1/$fan_{avg}$	$r=\sqrt{3*variance}$
He	ReLU and variants, ELU	2/$fan_{in}$	동일
LeCun	SELU	1/$fan_{in}$	동일

6. Code

🔸 Keras uses Glorot initialization (with a uniform distribution) by default
🔹 change to He initialization by using the he_uniform() or he_normal() function

keras.layers.Dense(10, activation="relu", kernel_initializer="he_normal")

🔹He initialization with a uniform distribution but based on $fan_{avg}$ rather than $fan_{in}$
: $fan_{in}$ 대신 $fan_{avg}$ 쓸 때

he_avg_init = keras.initializers.VarianceScaling(scale=2., mode='fan_avg', distribution='uniform')
keras.layers.Dense(10, activation="sigmoid", kernel_initializer=he_avg_init)

📌 Nonsaturating Activation Functions

🔸 이전에는 sigmoid activation function을 사용했었지만, vanishing, exploding gradients 문제가 발생하여 deep learning에 사용할 수 없게 됨
🔸 => ReLU 함수 사용. But ReLU 함수가 문제가 없는 것은 아님

1. Dying ReLUs

1) During training, some neurons effectively die => outputting only 0

🔸 Weighted sum of inputs is negative, output is 0 => unlikely to come back to life after updating weights
🔹 weighted sum의 input(x*w+b)이 0보다 작을 경우 activation function을 거친 output은 항상 0이 출력되어 neuron이 아예 죽어버림. backpropagation 진행하면서 해당 neuron이 학습에 영향을 미치지 않게 되어 아예 죽어버린 것처럼 됨

2) In some cases, half of neurons are dead, especially with a large learning rate

🔸 어떤 경우에는 neuron의 절반이 죽는 경우가 발생하며 특히 learning rate가 클 경우 발생하기 쉬움

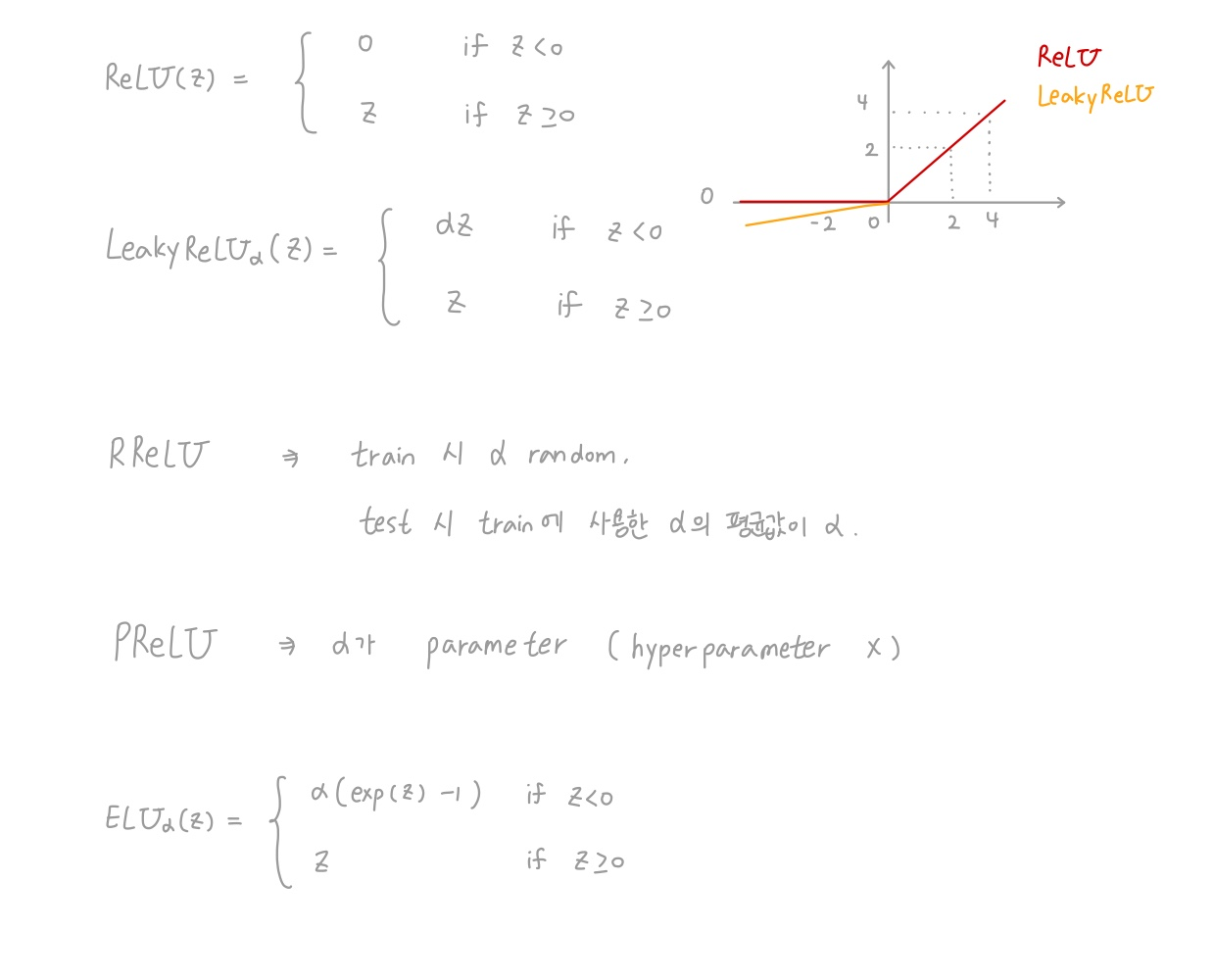
2. Leaky ReLU

🔸 입력값이 음수일 때 항상 0이 출력되는 것이 문제였기에 0이 아닌 출력을 내보냄

1) $LeakyReLU_{a}(z)$ = max($\alpha$z,z)

🔸 입력이 0보다 클 경우 ReLU와 동일하게 입력을 그대로 출력
🔸 입력이 0보다 작을 경우 $\alpha$만큼 scaling한 negative 값 출력, $\alpha$는 1보다 작은 값

2) hyperparameter 'a' defines how much the function "leaks": slope for z<0, typically 0.01

🔸 $\alpha$는 hyperparameter이기 때문에 설계할 때 값 정해줌
🔸 $\alpha$의 절댓값이 클 수록 음수의 절댓값 커짐
🔸 $\alpha$는 주로 0.01을 사용하지만, Dying ReLU가 발생하지 않을 경우 a를 0으로 해도 되고 문제에 따라 $\alpha$ 값 조절

3) never dies; may be in a long coma, but eventually wake up

🔸 neuron이 죽지는 않지만 긴 coma 상태에 빠질 수 있어 학습 시간이 오래 걸릴 수 있음

3. Randomized leaky ReLU (RReLU)

1) $\alpha$: random in a given range during training

🔸 train 도중 주어진 범위 내에서 random하게 선택
🔸 $\alpha$가 가질 수 있는 범위를 hyperparameter로 정해주지만 실제 $\alpha$값은 random하게 정해지며, $\alpha$ 값을 정해주는 Leaky ReLU와 다름

2) fixed to an average value during testing

🔸 test 과정에서는 train할 때 생성된 $\alpha$의 평균값으로 $\alpha$값 고정

3) a regularizer (reducing the risk of overfitting)

🔸 $\alpha$를 random하게 설정해주는 것이 regularizer의 역할을 해줌

💡 Leaky ReLU 학습 도중 overfitting이 발생하면 RReLU 사용

4. Parametric leaky ReLU (PReLU)

1) $\alpha$: a trainable parameter (not a hyperparameter)

🔸 parameter: 학습에 의해 학습된 결과. 사용자가 건들 수 없고 학습결과에 의해 결정됨
ex. weight, bias + $\alpha$
🔸 어떤 $\alpha$를 가질 때 가장 가장 좋은 결과가 나오는가
💡 train(학습): parameter를 구하는 과정

2) strongly outperform ReLU on large image datasets

3) on smaller datasets, risk of overfitting

🔸 큰 이미지 데이터셋의 경우 ReLU보다 성능이 좋지만, 작은 데이터셋의 경우 overfitting의 가능성 존재

5. Exponential linear unit (ELU)

🔸 input이 0보다 클 때 입력 그대로 출력
🔸 input이 0보다 작을 때 exponential 함수 이용해 출력 => 0 근처에서 값이 급격하게 감소. 0 근처가 입력에 가장 민감하게 반응
🔸 input이 일정 값 이하로 작아지면 일정한 상수 값 출력해 gradient가 0

1) outperformed all the ReLU variants in the experiments: Reduced training time and better performance on the test set

🔸 다른 모든 ReLU 함수들보다 성능이 좋음 => 학습 시간이 적게 소요되고 test set에 대한 성능이 좋음

2) negative values when z<0 => average output closer to 0 => alleviate the vanishing gradients

🔸 일정한 범위 내에 존재할 경우 (ex.[-1,1]) output의 평균이 0에 가까워 vanishing gradients를 완화시켜줌
🔸 vanishing gradients 해결 조건: 입력과 출력의 값의 분포가 표준화된 분포를 이루고 있어야함
🔸 입력 데이터와 출력 데이터가 일정 범위를 벗어날 경우(ex.[-1,1]외의 다른 부분) vanishing gradients 완화할 수 없음

3) -$\alpha$ for a large negative z. usually $\alpha$=1, but $\alpha$ is a hyperparameter

🔸 절댓값이 큰 음수의 경우, 출력이 -$\alpha$로 수렴. $\alpha$는 보통 1로 설정하여 사용하지만 hyperparameter이므로 사용자가 값을 바꿔 사용할 수 있음

4) nonzero gradient for z<0 => avoids the dying units issue

🔸 0 근처의 입력은 다른 입력들보다 더 큰 gradient를 갖게되므로 dying unit issue를 피할 수 있음

5) smooth around z=0 => speed up Gradient Descent

🔸 다른 leakyReLU는 z=0일 때 불연속인데 ELU의 경우에는 gradient 값이 continuos한 값을 갖기 때문에 Gradient Descent 방식에서 학습 속도를 높일 수 있음

6) slower to compute due to exponential function

🔸 exponential function을 사용하기 때문에 연산량이 증가
🔸 During training, compensated by the faster convergence rate
🔹 train할 때에는 수렴 속도가 빠르기 때문에 학습에 필요한 epoch 수가 줄어들기 때문에 학습 속도가 느리다고 할 수 없음
🔸 At test time, slower than a ReLU networt
🔹 test할 때에는 feed forward 할 시 layer마다 한 번씩 exponential 연산이 들어가 ReLU에 비해 느림

💡 inference의 목적은 현재 데이터에 대해서 해당 모델이 원하는 작업을 수행 => test

6. Scaled Exponential linear unit (SELU)

1) Exclusive stack of dense layers with SELU activation (for hidden): self-normalize

🔸 Dense layer만으로 구성된 네트워크에서 사용 가능

2) output of each layer: m=0 and σ=1 during training => solves vanishing/exploding gradients problem

🔸 각 layer의 activation function이 SELU이기에 각 layer의 출력은 m=0, σ=1로 나타나고 이는 vanishing gradients problem을 해결할 수 있음

3) often significantly outperforms other activation functions for such neural nets

🔸 SELU가 다른 activation function들보다 성능이 좋음

4) a few conditions for self-normalization to happen => 조건

🔸 input features must be standardized (m=0 and σ=1)
🔸 hidden layer's weights: initialized with LeCun normal initialization

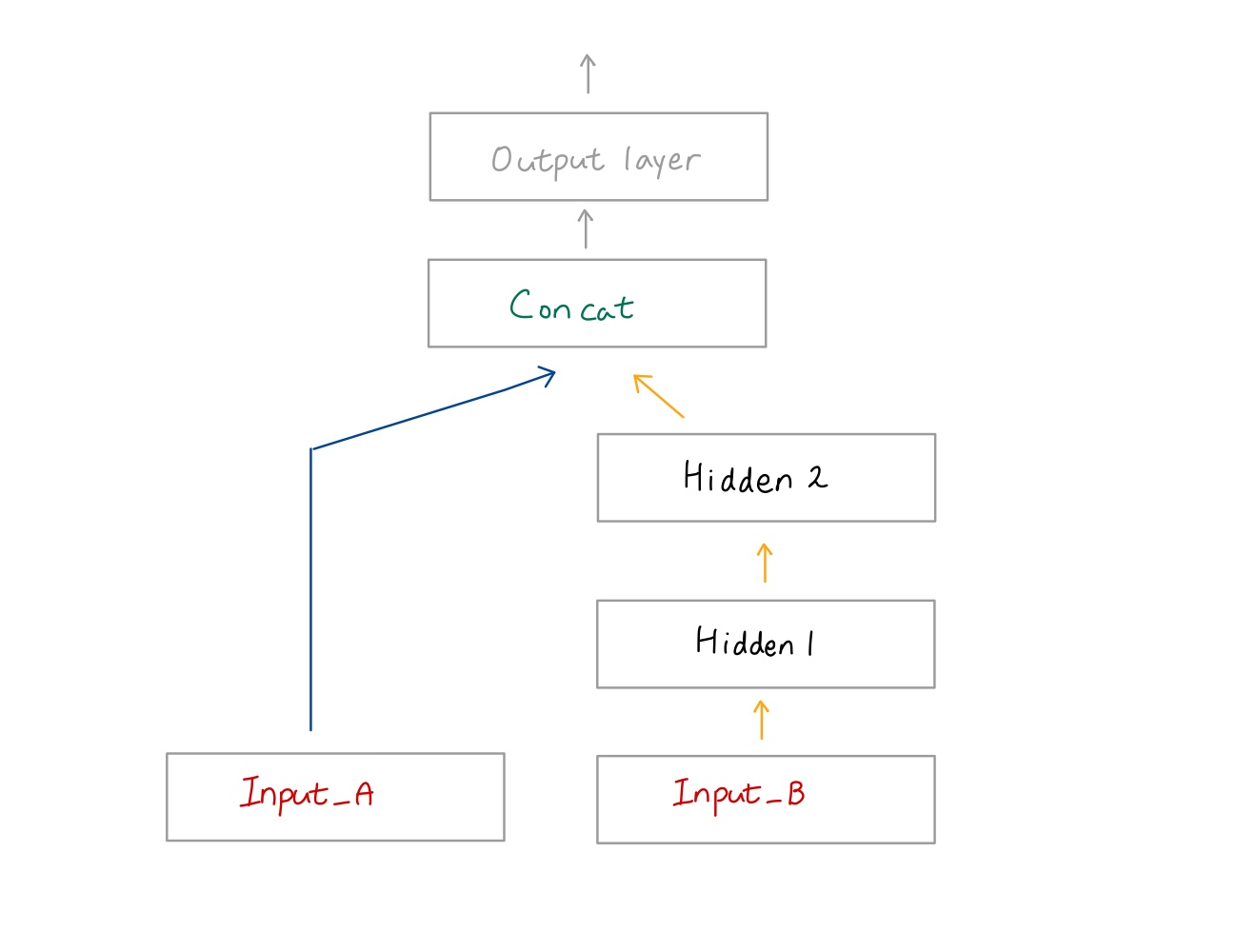
kernel_initializer = "lecun_normal"

🔸 Sequential architecture only: self-normalization will not be guaranteed for nonsequential architectures or networks with skip connections
🔹 사실상 가장 중요한 조건으로, sequential achitecture에서만 적용 가능하고 nonsequential architecture이거나 skip connection을 가질 경우 적용되지 않음
🔹 Sequential architecture란 입력이 들어갔을 때 모든 hidden layer를 거쳐 output을 출력하는 구조. nonsequential architecture의 예시로 아래 그림이 있음

5) can improve performance in convolutional neural nets as well

7. In general, SELU > ELU > leaky ReLU(and its variants) > ReLU > tanh > logistic(sigmoid)

1) Conditions not met: ELU

2) Runtime latency issue: leaky ReLU

🔸 inference할 때 최대한 빠르게 출력을 얻어야한다면 ELU가 적합하지 않으므로 leaky ReLU 사용

3) With spare time and computing power: cross-validation to evaluate other activation functions

🔸 충분한 시간과 computing power가 있다면, 여러 activation function을 진행한 후 가장 성능이 좋은 activation function 찾는 것이 가장 좋음
🔸 PReLU when overfitting
🔹 leaky ReLU 사용시 overfitting 발생하면 PReLU 사용
🔸 PReLU for huge training set
🔹 training set이 큰 경우 PReLU 사용

8. Keras 구현

1) LeakyReLU

model = keras.models.Sequential([
	keras.layers.Dense(10, kernel_initializer="h_normal"),
    keras.layers.LeakyReLU(alpha=0.2),
    [...]
])

2) PReLU

keras.layers.PReLU(alpha=0.2)

3) SELU

layer = keras.layers.Dense(10, activation="selu", kernel_initializer="lecun_normal")

4) no official inplementation of RReLU: implement by yourself

🔸 RReLU는 keras가 지원하지 않아 직접 코드 짜야함

📌 Batch Normalization

1. Internal Covariate Shift proble: the parameters of the previous layers change => the distribution of each layer's inputs changes during training

🔸 Initialization과 nonsaturating activation function을 이용해 vanishing, exploding 문제 해결
🔸 But internal covariate shift 문제 존재
🔸 train이 진행되면서 이전 layer의 parameter(weight, bias)가 변함 => 각 layer의 입력 데이터의 distribution이 변함 => vanishing, exploding 문제 다시 발생할 가능성 있음

2. adding an operation just before or after the activation function of each layer

🔸 각 layer의 activation function 앞뒤에 operation 넣기

operation 1) simply zero-centering and normalizing the inputs

🔸 input의 분포를 standardization해 평균이 0, 표준편차가 1이 되도록 함

operation 2) then scaling and shifting the result using two new parameters

🔸 두개의 새로운 parameter를 이용하여 결과를 scaling하고 shifting, 이때 parameter는 training parameter로 학습을 통해 결정되는 값

1) let the model learn the optimal scale and mean of the inputs for each layer

🔸 각 layer의 입력의 최적의 scale과 mean 학습시키기

3. Mean and SD at test: whole training set's mean and standard deviation after training

🔸 train할 때는 minibatch에 대해 mean과 standard deviation을 구하면 되는데, test에서는 data가 minibatch로 들어오지 않을 수도 있고 data가 하나만 들어올 수도 있음
🔸 train 끝난 후 전체 train data set의 평균(mean)과 표준편차(SD)를 구해 고정

1) typically efficiently computed during training using a moving average: Keras BatchNormalization

🔸 Keras BatchNormalization 사용할 경우 train 하면서 평균과 표준편차 누적해 계산

2) Y(scale), B(offset): learned

🔸 학습하면서 값 결정

3) m(mean), and σ(sd): estimated using exponential moving average, used after training

🔸 train 끝난 후 exponential moving average 이용해 값 결정
🔸 위에서 말한 것과 같이 keras나 다른 library를 사용하면 train 진행하면서 moving average 형태로 값 계산

4. Pros

1) Reduced vanishing gradients problem(even with tanh and logistic activation)

🔸 Batch normalization의 목적은 layer에 들어가는 모든 입력의 분포를 일정하게 유지시키는 것 => tanh와 logistic을 activation으로 사용해도 vanishing gradient 문제 줄여줌

2) Less sensitive to the weight initialization

🔸 He, Glorot, LeCun 등의 initialization을 사용하지 않아도 vanishing gradient 문제 억제해줌

3) much larger learning rates => significantly speeding up

🔸 learning rate를 증가해도 되기에 step 수가 줄어들고 학습 속도가 빨라짐
🔸 same accuracy with 14 times fewer training steps

4) Acts like a regularizer, reducing the need for other regularization techniques (drop out)

🔸 regularizer의 역할을 하기에 overfitting 발생하지 않음

5. Cons

🔸 각 layer마다 BN이 들어가야하기때문에 runtime시 별도의 연산 필요해 prediction(=inference)하는데 시간이 더 소요됨

1) Slower predictions due to the extra computations at runtime

🔸 Although it removes the need for normalizing the input data
🔹 input data를 normalization할 필요는 없어지지만, input data normalization은 전체 network에서 한 번 수행하지만 BN은 각 layer마다 수행해야하므로 연산량이 훨씬 많음
🔸 Often possible to fuse the BN with the previous layer (TFLite's optimizer)

2) Check how well plain ELU + He initialization perform before playing with Batch Normalization

🔸 train 후 inference에서 computation penalty가 주어지는데 penalty가 허용할 수 있는 범위 내에 존재하지 않을 경우, Batch Normalization으로 학습하기 전 ELU와 He initialization으로 수행
🔸 => 학습이 잘 될 경우 ELU + He initialization만을 통한 학습 진행해 inference 시간 단축
🔸 => 학습이 잘 되지 않을 경우 Batch normalization 진행

📌 Implementing Batch Normalization with TensorFlow

1. BN after activation and as the first layer

import tensorflow as tf
from tensorflow import keras

model = keras.models.Sequential([
	keras.layers.Flatten(input_shape=[28,28]),
    keras.layers.BatchNormalization(),
    keras.layers.Dense(300, activation="elu", kernel_initializer="he_normal"),
    keras.layers.BatchNormalization(),
    keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal"),
	keras.layers.BatchNormalization(),
	keras.layers.Dense(10, activation="softmax")
])

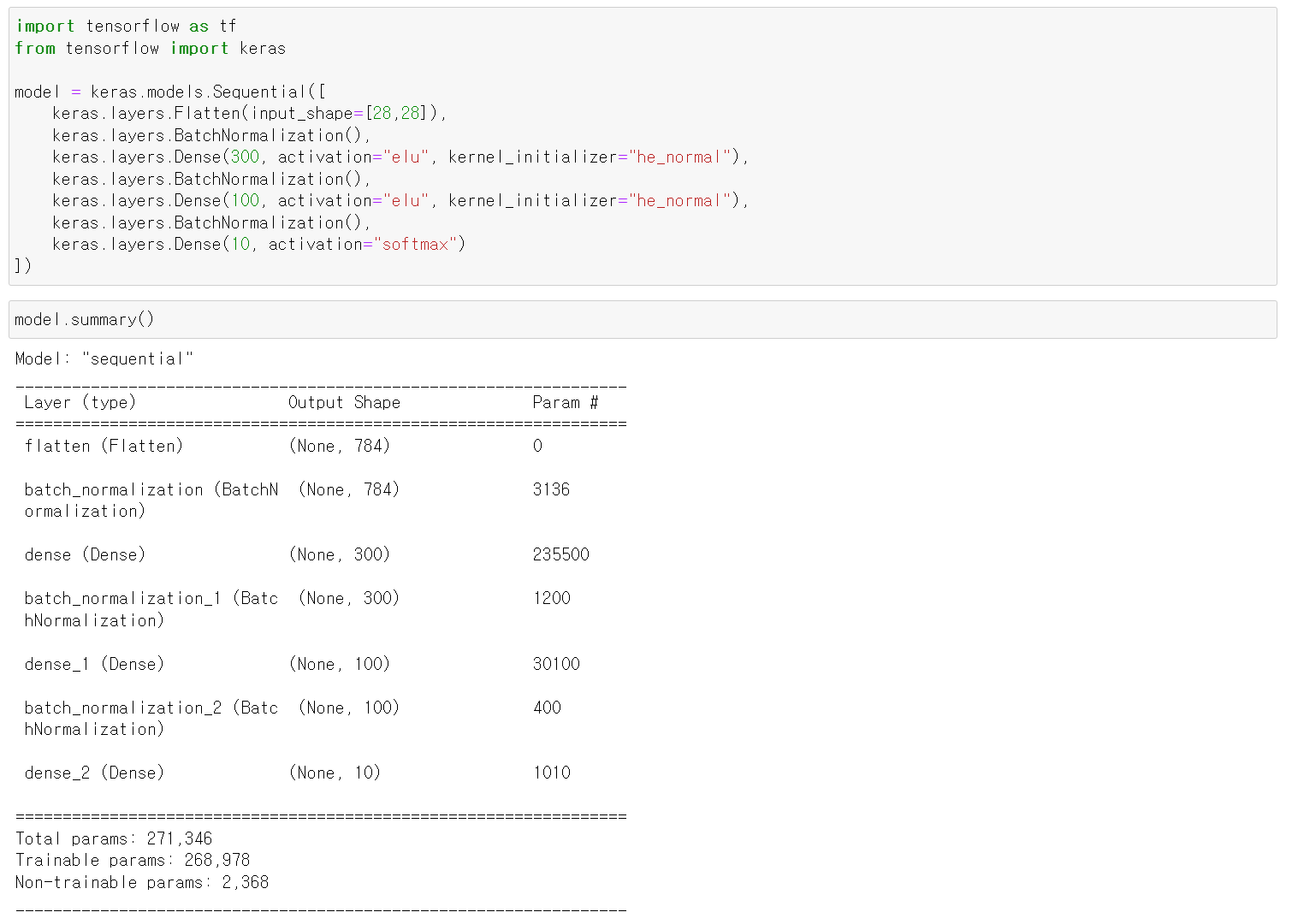
2. BN_v2: 4 parameters per input

🔸 4 parameters: $m$, σ, $\gamma$, $\beta$
🔸 input 784개 * parameter 4 = 3136이 총 파라미터 개수 (param #)

3. $m$, σ: non-trainable

🔸 $m$와 σ는 학습을 통해 얻어지는 값이 아니라 minibatch의 평균과 표준편차를 구한 것
🔸 BN의 parameter 개수를 모두 더해서 반으로 나눈 값이 non-trainable 값 (parameter 4개 중 2개가 non-trainable)

4. batch_normalization_v2의 variable의 이름과 trainable 확인

🔸 True, False가 trainable 나타냄

[(var.name, var.trainable) for var in model.layers[1].variables]

5. BN in Keras

🔸 BN layer를 생성하면 2 operation 생성. 별도로 명령 수행하지 않아도 자동으로 수행해줌
🔸 Keras calls two (TF) operations: updating moving averages ($m$, σ)

6. BN before activation

🔸 앞에서는 BN이 activation 뒤에 존재하는 경우였고 이번엔 activation 앞에 존재하는 경우
🔸 activation의 default는 None이므로 activation 없이 layer 생성한 후 BN 진행 후 activation 할당
🔸 use_bias=False
: beta라는 parameter(offset)에 bias 포함할 수 있기 때문에 굳이 b 학습할 필요 없음

model = keras.models.Sequential([
    keras.layers.Flatten(input_shape=[28,28]),
    keras.layers.BatchNormalization(),
    keras.layers.Dense(300, kernel_initializer="he_normal", use_bias=False),#activation 없이 layer 생성
    keras.layers.BatchNormalization(),#BN 수행
    keras.layers.Activation("elu"),#activation function 넣기
    keras.layers.Dense(100, kernel_initializer="he_normal", use_bias=False),
    keras.layers.BatchNormalization(),
    keras.layers.Activation("elu"),
    keras.layers.Dense(10, activation="softmax")
])

7. Hyperparameters to tweak

🔸 momentum
🔹 v: new vector of input means or standard deviations computed over the current batch, 현재 batch의 mean과 standard deviation 계산한 값
🔹 v^ (v위에 ^): running average, v를 running average한 값
🔹 typically close to 1 (default: 0.99): more 9s for larger datasets and smaller mini-batches: dataset이 크고 minibatch가 작으면 momentum을 1에 가깝게 설정
🔹 현재의 batch에 (1-momentum)만큼의 가중치를 주고, running average에 momentum만큼의 가중치를 줘서 새로운 running average를 만드는 방법. momentum이 1이면 현재의 batch 값 사라지고, 0이면 지금까지의 running average가 0이 됨

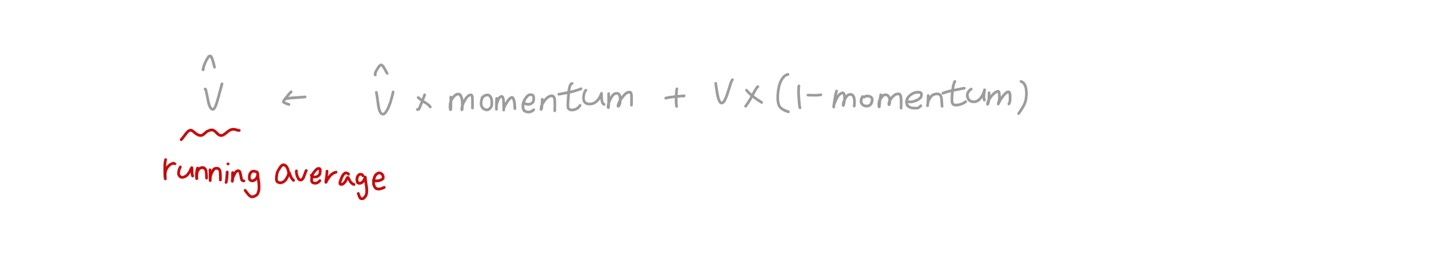
🔸 axis: axis for normalization(default:-1 (last axis))
🔹 axis 기본값은 -1로 가장 마지막의 axis feature에 대해 normalization 진행
🔹 들어오는 입력 데이터에 대해 normalization 진행하는데, 입력데이터의 shape이 보통 [batch size, feature]로 구성되어 있음. 이 경우는 feature가 1dimension의 경우이고, 2 dimension의 경우에는 [batch size, height, width]와 같이
🔹 previous ex. Input shape [batch size, features] after flatten: normalization over 784 features => 이 경우는 feature가 1dimension의 경우이고 axis를 지정하지 않아도 feature가 됨

🔹 [batch size, height, width] before flatten: axis=[1,2] => feature가 2 dimension이 되는 경우로 default 값으로 진행하면 normalization은 width만 진행됨. 모든 feature에 대해 진행해야하므로 height와 width가 모두 진행되도록 axis=[1,2] 설정

8. Remind the different behavior during training and testing

🔸 BN은 train과 test 시 동작이 다름

9. BatchNormalization has become one of the most-used layers in deep neural networks

🔸 Deep neural network에서 BN 가장 많이 사용
🔸 often omitted in the diagrams: BN after every layer. diagram마다 BN을 그리기 어려우므로 빼서 그리지만 모든 layer에 BN이 존재한다는 것 명심

📌 Gradient Clipping

🔸 exploding gradient의 해결방안 => gradient clipping

1. Clip the gradients during backpropagation not to exceed some threshold

🔸 gradient를 clip해서 backpropagation 동안 특정 threshold를 넘지 않도록 함
🔸 sgd optimizer 지정 시 clipvalue 지정

1) to lessen the exploding gradients problem

🔸 vanishing gradient 외에도 exploding gradient도 문제 => 주로 RNN에서 발생

2) mostly useful for RNN (recurrent neural networks)

threshold = 1.0
optimizer = tf.keras.optimizers.SGD(clipvalue=threshold)
model.compile(optimizer=optimizer, loss="mse")

3) Values are clipped between -1.0 and 1.0

🔸 -1과 1 사이로 clipping되서 값이 이 밖으로 벗어나지 않음. 1보다 크면 1로 clipping => exploding gradient 발생하지 않음
💡 threshold를 1로 지정하면 0~1이 아니라 -1~1 범위

4) Ex. Gradient vector of [0.9, 100]: pointing in the direction of the $2^{nd}$ axis

🔸 Clipping by value: [0.9, 1.0] => diagonal direction
🔹 clip하면 [0.9, 100]이 [0.9, 1.0]이 되어 vector의 방향이 달라짐 => clip by norm 사용
🔸 Clipping by norm: [0.00899964, 0.9999595] => preserving direction
🔸 Clipnorm = 1.0
🔹 clip by norm 사용해 axis의 비율대로 값을 줄여 vector의 방향을 일정하게 유지

5) Try clipvalue and clipnorm with different values

🔸 어떤 경우는 clipvalue가 좋은 결과를 낼 수도 있기 때문에 clipnorm만 사용하는 것이 좋은것은 아님