<인공신경망>05. Keras를 이용한 MLP 구현(2):모델학습, 평가 및 추론

📌 학습 과정

1. dataset 준비
2. model 생성
3. model compiling
4. fit(학습)
5. evaluate
6. generalization해서 사용 => prediction(=inference)

📌 Compiling the model

1. compile() method: to specify the loss function and the optimizer to use

🔸 compile() method 사용해서 loss function과 optimizer를 지정하고 어떤 metrics을 사용해서 regression할지 결정
🔸 Optionally, specify a list of extra metrics to compute during training and evaluation

model.compile(loss="sparse_categorical_crossentropy", optimizer="sgd", metrics=["accuracy"])

1) loss = keras.losses.sparse_categorical_crossentropy

🔸 위 코드의 loss = "sparse_categorical_crossentropy" 와 같은 의미
🔸 multiclass output with integer labels(sparse labels)일 경우 사용하는 loss function
🔹 integer label로 하나씩 mapping될 수 있고 그러한 output이 3개 이상의 multiclass를 가질 경우 사용
🔸 categorical_crossentropy: multiclass output with one-hot encoding labels
🔹 one-hot code: 8개의 bit가 있고 1의 위치에 따라 class 결정
ex. binary encoding의 경우 0000,0001,0010 등으로 진행, one-hot code의 경우 00000001, 00000010,00000100 등으로 진행
🔸 cf) binay classification의 경우 binary_crossentropy 사용
🔸 binary code와 one-hot code (binary(=sparse) label과 one-hot label)변환
🔹 Binary->One-hot: keras.utils.to_categorical() function
🔹 One-hot->Binary: np.argmax() function with axis=1
💡 loss function 달라지면 학습 결과 달라짐

2) optimizer = keras.optimizers.SGD(): default learning rate = 0.01 or "SGD(learning rate=??)"

🔸 train 진행하면서 각 iteration마다 learning rate를 어떻게 적용할지
🔸 Stochastic Gradient Descent 방식
🔸 default learning rate는 0.01이고 바꾸고 싶으면 SGD(learningrate=x)로 작성(이때 x는 원하는 learning rate 값)
💡 optimizer는 학습 속도와 효율에 영향 미침

Stochastic Gradient Descent

: Loss Function을 계산할 때, 전체 데이터(Batch) 대신 일부 데이터의 모음(Mini-Batch)를 사용하여 Loss Function을 계산

3) metrics = [keras.metrics.sparse_categorical_accuracy]

🔸 regression할 때 어떤 값을 가지고 평가할 것인지

📌 Training and evaluating the model

1. fit() method

1) 학습 진행

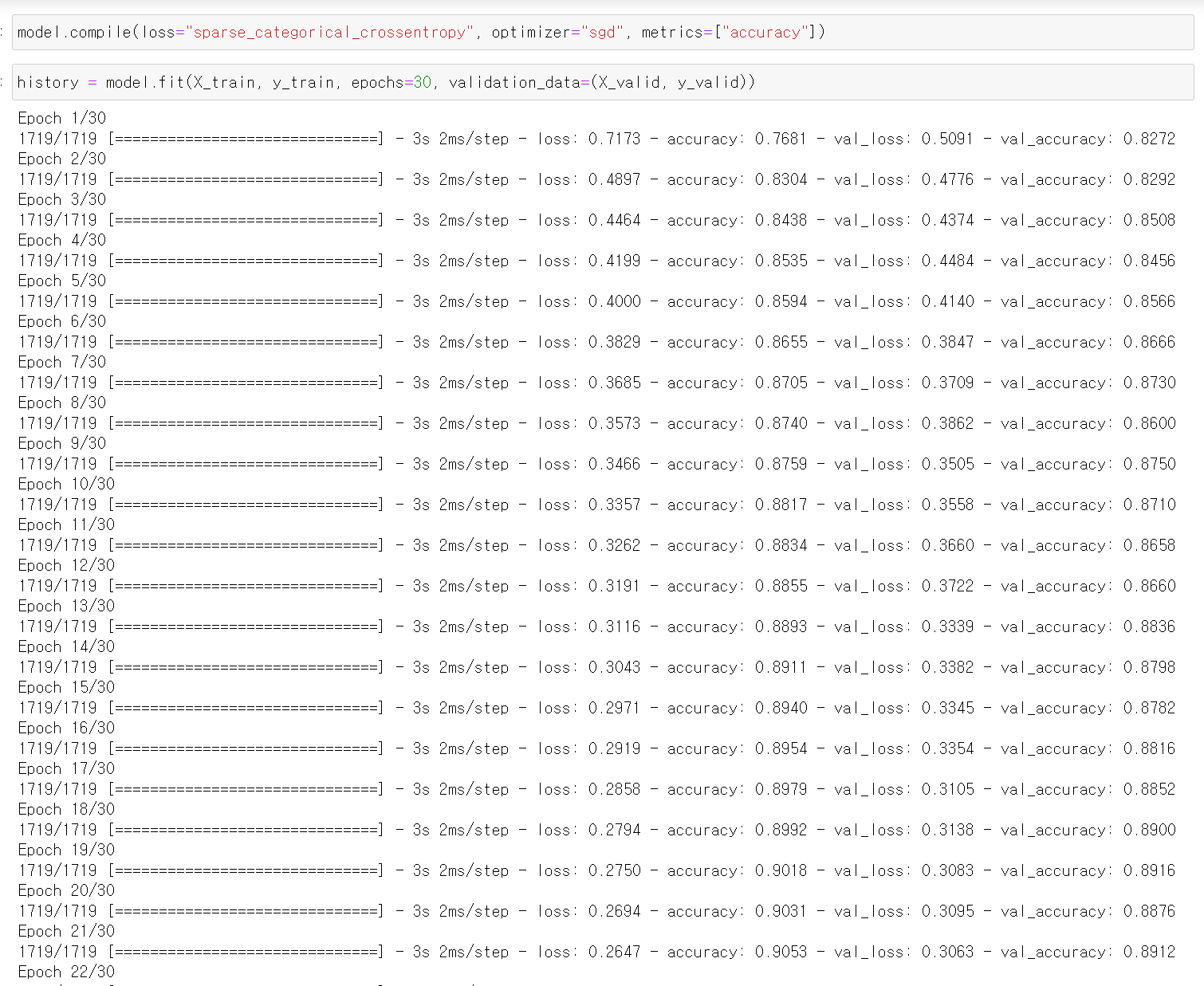
history = model.fit(X_train, y_train, epochs=30, validation_data=(X_valid, y_valid))

🔸 epoch: 학습을 얼마나 진행할지, validation을 지정하지 않았을 경우 validation_split=0.1 하면 train data가 90%, validation data가 10%
🔸 60,000개의 train_full 중 55,000개를 train data로, 5,000개를 validation data로 설정했음
🔸 epoch을 30으로 지정했으므로 55,000개의 train data를 훈련시키고 5,000개의 validation으로 검증하는 하나의 epoch이 30번 진행됨
🔸 결과에서 보이는 첫번째 loss와 accuracy는 55,000개의 train data에 대한 결과이고, 두번째 나타난 val_loss와 val_accuracy는 5,000개의 validation data에 대한 결과

2)

🔸 훈련 출력 시에는 validation set을 제외한 train data의 개수가 한 epoch 구성
🔸 학습 속도 확인할 때, 3s 보다 2ms/step과 같이 step 더 정확함
🔸 Loss/accuracy: how well the model really performs
🔹 model이 얼마나 좋은 성능을 가지고 있는지
🔸 If performance on the training set is much better than on the validation set => model is probably overfitting (or there is a bug, such as a data mismatch)
🔹 performance는 loss와 accuracy 의미
🔹 일반적으로 train set의 loss와 accuracy가 validation set보다 성능이 좋게 나타나는데, 그 차이가 너무 크면 overfitting된 것
💡 Good sign of training
1. Training loss decreases 2. validation accuracy increase 3. training and validation accuracies are close 4. reasonable validation accuracy

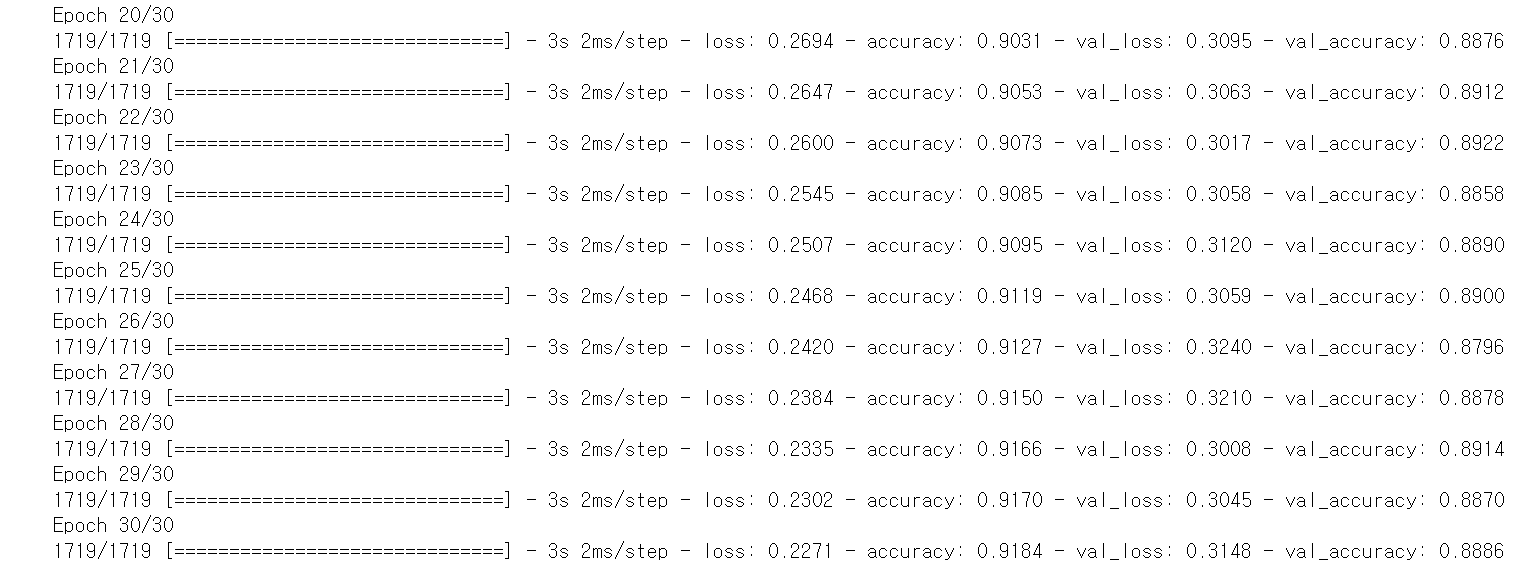
3) 🌟 결과 분석

1. 훈련은 train data의 accuracy가 1이 될 때까지 진행
2. 훈련 초기의 train data의 loss 값이 급격히 줄어들고 accuracy 값은 급격히 증가해야 훈련이 잘 진행된 것. train data의 초기 loss가 천천히 떨어지면 학습이 정상적으로 진행되고 있는지 확인해야함 => 모델 생성, 모델 컴파일 시 옵션(파라미터)이 잘 들어갔는지, 데이터가 잘 들어가는지 등
3. train data의 loss와 accuracy는 각각 급격히 감소하고 증가하는데에 반해 validation data의 loss와 accuracy 변화 차이는 train data에 비해 작음
4. 지정한 epoch 수 전에 train loss 값의 감소가 거의 없다면 학습을 멈추어도 되며, 반대로 마지막과 그 전 epoch의 변화가 있다고 판단되면 epoch 수를 늘려 더 학습시켜야함
5. train loss가 증가함에 따라 train accuracy의 감소를 보는 것이 아니라, train loss가 증가함에 따라 validation accuracy의 감소를 지켜봐야함. train loss의 변화가 있어도 validation accuracy의 변화가 없다면 멈춰야함
6. 일반적으로 훈련이 모두 끝났을 때의 train accuracy가 val_accuracy보다 반드시 좋게 나타나는데, 그 차이가 크면 overfitting이 발생한 것이므로 reguralization을 해서 다시 훈련시킬 것(overfitting이 아닐 경우 data가 맞지 않는 등의 원인이 있을 수 있음)

2. Skewed dataset

🔸 class마다 비슷한(충분한) 숫자의 data를 가지고 있는 것이 좋음
🔸 전체적인 data set의 개수를 유지하기 위해 사용

1) class_weight: give a larger weight to underrepresented classes

🔸 data가 충분하지 않은 class에 더 큰 weight 부여
🔸 data가 충분한 class는 훈련하면서 더 자주 사용되므로 weight에 영향을 많이 미치기 때문

2) sample_weight: Per-instance weights.

🔸 각 instance마다 서로 다른 weight 부여
🔸 Ex. Labeled by experts and using a crowdsourcing platform => give more weight to the experts
🔹 전문가가 label한 instance는 대중이 label한 instance보다 더 높은 weight 부여

3) both class_weight and sample_weight: multiplied

🔸 class_weight와 sample_weight를 모두 사용할 경우 weight multiplied한 weight 부여

3. History object

1) training parameters (history.params)

2) list of epochs (history.epoch)

3) dictionary containing the loss and extra metrics (history.history): most important

💡 history plot 코드

import pandas as pd
import matplotlib.pyplot as plt
pd.DataFrame(history.history).plot(figsize=(8,5))
plt.grid(True)
plt.gca().set_ylim(0,1)	#set the vertical range to [0,1]
plt.show()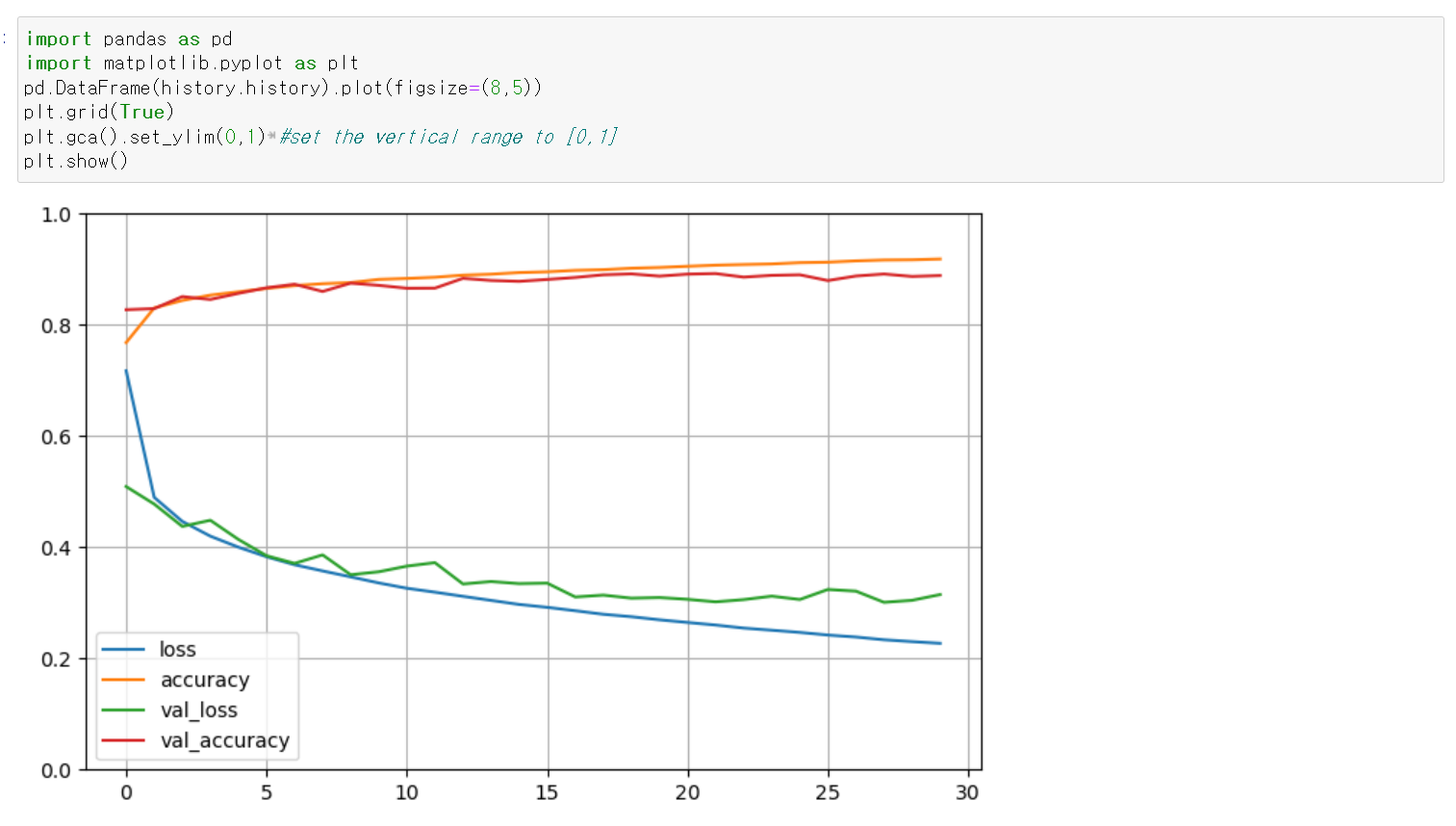

🔸 위에 작성한 history plot의 x축은 epoch을 의미
🌟 그래프 분석
1. train loss와 train accuracy가 각각 훈련 끝에 validation loss와 validation accuracy보다 성능이 좋아야함
2. train loss는 학습 초기에 급격하게 떨어져야함. 훈련 전반적으로 loss는 accuracy가 올라가는 것보다 더 빠른 속도로 떨어짐. accuracy는 기울기가 작아 saturation된 것으로 판단할 수 있기 때문에 성능이 개선되어있는지 볼 때에는 loss값을 봐야함.
3. train accuracy와 validation accuracy는 나란히 가야함. 차이가 많이 날 경우 overfitting 발생한 것

4) validation error at the end of each epoch, while the training error using a running mean during each epoch => training curve should be shifted by half an epoch to the left

🔸validation loss는 각 epoch이 끝날 때 한 번에 계산되는데, training loss는 각 epoch의 running mean을 의미. 즉 train loss는 한 epoch에 여러 minibatch가 존재하는데, minibatch가 끝날 때마다 그 전의 loss와의 평균을 계산해 나타냄. 따라서 처음 하나의 minibatch의 loss가 0.7, 그 다음 minibatch의 loss가 0.5이면 그 다음 minibatch의 총 loss는 평균인 0.6이 됨. 따라서 실제 minibatch의 loss 값은 그래프 상의 loss보다 더 작음

5) validation loss is still going down => continue training

🔸 validation loss가 epoch이 끝날 때까지 계속해서 작아지고 있으므로 epoch 수를 늘려 훈련을 더 진행해야함

4. For better performance, check

1) Learning rate

2) Optimizer

3) Model (hyperparameters): # of layers, # of neurons per layer, type of activation

🔸 model parameter는 weight와 bias 의미
🔸 model hyperparameter는 # of layers, # of neurons per layer, type of activation

4) Other hyperparameters: batch size

🔸 training hyperparameter: batch size, # of epoch 등

5. Evaluation

1) evaluate model on the test set: to estimate the generalization error

🔸 test set으로 evaluate한 값이 generalization error
🔸 출력으로 train data의 개수만큼 한 epoch으로 나타남

model.evaluate(X_test, y_test)

💡 train은 forward pass와 backward pass 모두 거치고, evaluate는 forward pass만 하기 때문에 시간 짧게 소요

2) slightly lower performance on the test set than on the validation set

📌 Using the model to make preditions

🔸 train 또는 test data set에 존재하지 않는 새로운 data prediction(= inference)
🔸 But fashion MNIST의 경우 새로운 instance가 없기 때문에 X_test 중 하나의 data 사용

1. make predictions on new instances

import numpy as np

X_new = X_test[:3]
y_proba = model.predict(X_new)
y_proba.round(2)	#소수점 2자리까지 표기
y_pred = np.argmax(y_proba, axis=-1)	#y_proba 중 가장 값이 큰 argument 출력
np.array(class_names)[y_pred]	#해당 class와 class name mapping, 각 class가 어떤 것인지 모르므로 별도로 표기해 출력
y_new = y_test[:3]	#위 코드까지가 실제로 사용되고 결과값은 없는 경우가 많으므로 위 결과를 믿고 사용해야함.
y_new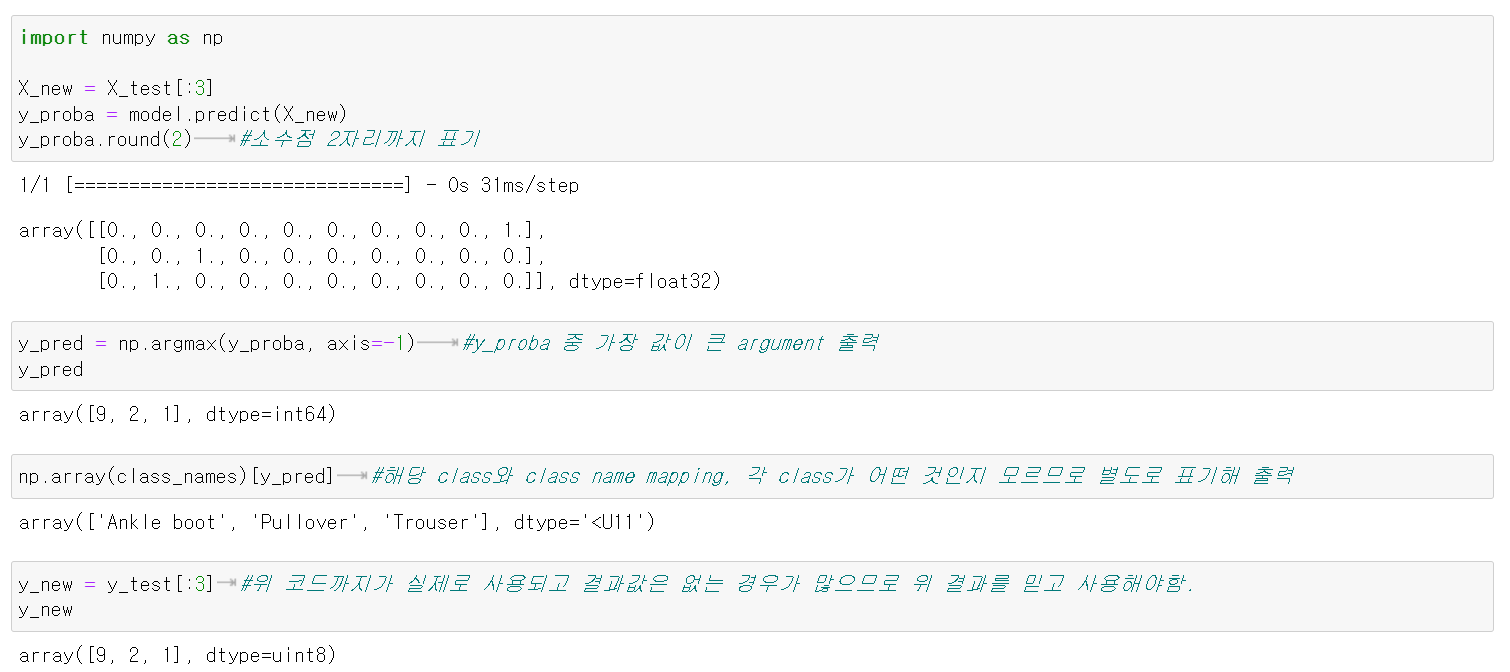

🔸 분석
1. y_proba한 결과를 소수점 2자리까지 표기한 결과를 보면, 첫번째 list는 X_test[0]이 해당 item일 각각의 확률 나타내고 두번째, 세번째 list도 각각 2번째 instance, 3번째 instance를 나타냄
ex. 첫번째 instance는 0,1,2,3,4번째 class일 확률이 0, 5번째 class일 확률이 0.03, 6번째일 확률이 0, 7번째일 확률이 0.01, 8번째일 확률이 0, 9번째일 확률이 0.96으로 9번째 class인 Ankle boot로 predict

🌟 지금까지 classification MLP building. 이제 regression MLP building

🌟 Regression

📌 Building a Regression MLP Using the Sequential API

1. California housing problem using a regression neural network

1) Data preparation: Load, split, and scale dataset

from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
housing = fetch_california_housing()
X_train_full, X_test, y_train_full, y_test = train_test_split(housing.data, housing.target)
X_train, X_valid, y_train, y_valid = train_test_split(X_train_full, y_train_full)
scaler = StandardScaler()	#fashion MNIST에서 255로 나눈 것이 scaling
X_train = scaler.fit_transform(X_train)	#fit_transform()은 학습시키고 변환
X_valid = scaler.transform(X_valid)	#transform은 변환만
X_test = scaler.transform(X_test)

Standard

모든 data(instance)를 평균이 0이고 분산이 1인 정규 분포로 만드는 것

2) Similar procedure to classification except for single neuron output without activation

🔸 classification의 경우 multiclass 였으므로 출력이 여러개였지만, regression의 경우 output neuron이 하나이므로 activation function은 없어야함
🔸 그 외에는 classification과 동일

3) Loss function: MSE

4) Noisy dataset => single hidden layer with fewer neuron to avoid overfitting

🔸 noisy dataset의 경우 overfitting이 발생할 확률이 높아 hidden layer를 하나만 설정하고, neuron도 적게 설정해 단순한 모델 사용

5) model 생성

model = keras.models.Sequential([
	keras.layers.Dense(30, activation="relu", input_shape=X_train.shape[1:]),
    keras.layers.Dense(1)])
model.compile(loss="mean_squared_error", optimizer="sgd")
history = model.fit(X_train, y_train, epochs=20, validation_data=(X_valid, y_valid))
mse_test = model.evaluate(X_test, y_test)
X_new = X_test[:3]
y_pred = model.predict(X_new)

🔸 layer 생성 시 input_shape=X_train.shape[1:]을 한 이유는 X_train.shape만 했을 경우 => 앞의 11610은 입력으로 들어갈 데이터의 수

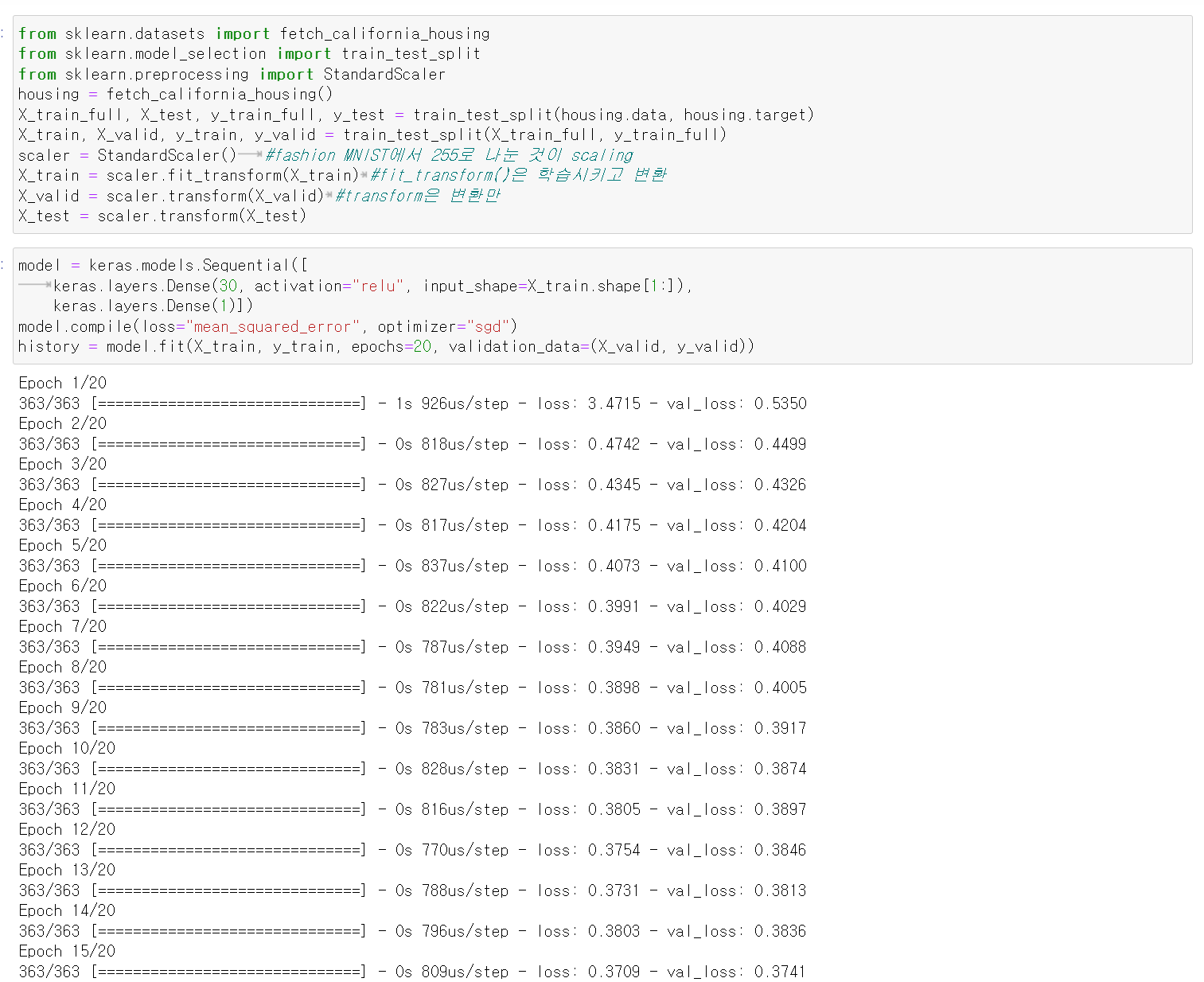
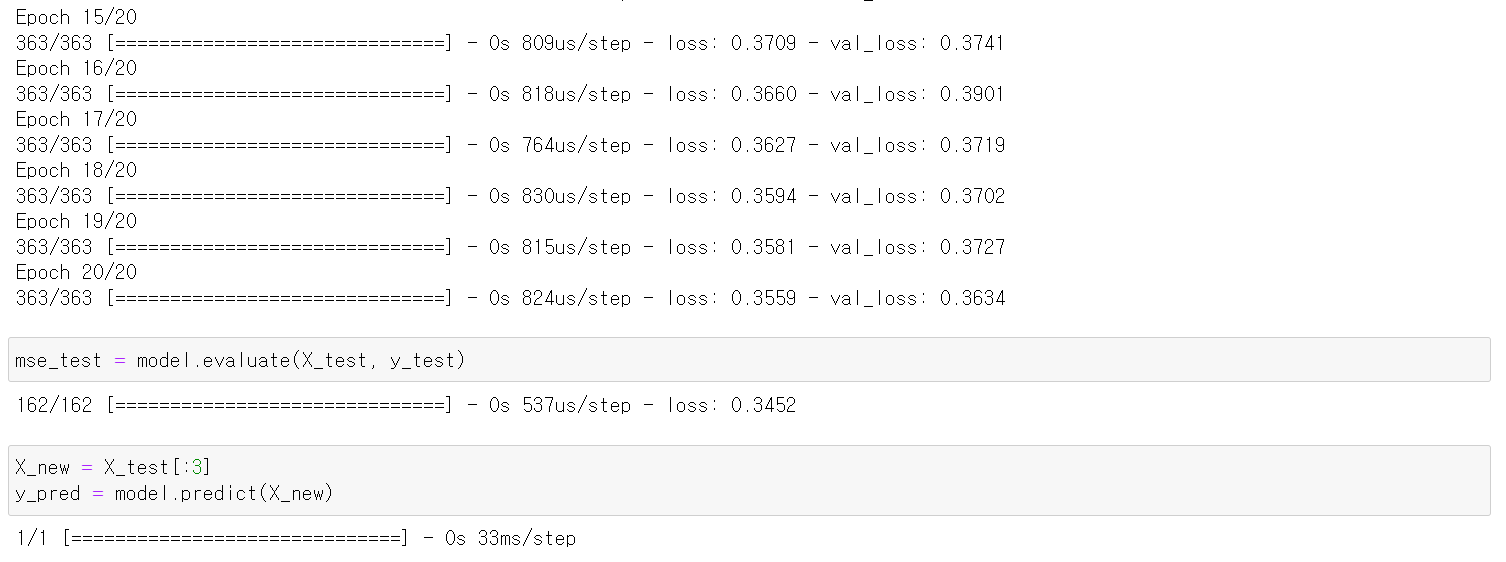
🔸 regression에서는 mse를 보고 얼마나 학습이 잘 되었는지 확인