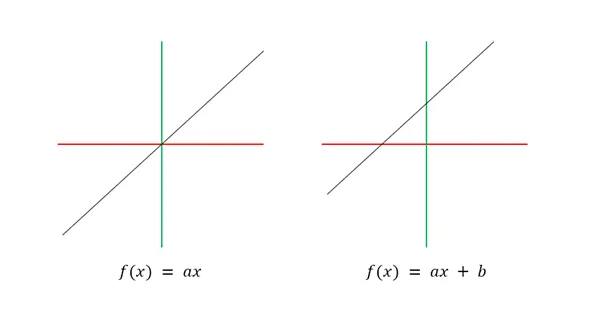선형성

Woogie_·2025년 5월 20일
게임 수학

게임 수학

목록 보기
6/15

선형성 (Linearity, 線型性)

선형성의 정의

  • 가산성 (Additivity) : f(x+y)=f(x)+f(y)f(x+y)=f(x)+f(y)
  • 1차 동차성 (Homogeneity of 1 degree): af(x)=f(ax)af(x)=f(ax)
  • 두 조건을 모두 만족할 때 선형성을 갖는다.

선형성을 만족하는 함수 찾기

예제 함수)

f(5+10)=f(5)+f(10)5f(10)=f(50)f(5+10)=f(5)+f(10) \\ 5f(10)=f(50)

  • f(x)=xf(x) =x

    15=5+1050=5015=5+10\\ 50=50

  • f(x)=2xf(x)=2x

    2⋅15=2⋅5+2⋅105⋅(2⋅10)=2⋅502\cdot 15=2\cdot 5+2\cdot 10\\ 5\cdot (2\cdot 10)=2\cdot 50

  • f(x)=2x+1f(x)=2x+1

2⋅15+1≠(2⋅5+1)+(2⋅10+1)5⋅(2⋅10+1)≠2⋅50+12\cdot 15 + 1\ne(2\cdot 5 + 1)+(2\cdot 10 + 1)\\ 5\cdot (2\cdot 10 + 1)\ne 2\cdot 50 + 1
  • f(x)=x2f(x)=x^2
15⋅15≠5⋅5+10⋅105(10⋅10)≠50⋅5015\cdot 15\ne5\cdot 5+10\cdot 10\\ 5(10\cdot 10)\ne50\cdot 50
  • f(x)=axf(x)=ax
f(b+c)=f(b)+f(c)a(b+c)=ab+acf(b+c)=f(b)+f(c)\\ a(b+c)=ab+ac
kf(b)=f(kb)kab=akbkf(b)=f(kb) \\ kab = akb
∴f(x)=ax는선형성을만족한다.\therefore f(x)=ax 는 선형성을 만족한다.
  • f(x)=ax+bf(x)=ax+b
f(c+d)=a(c+d)+b=ac+ad+bf(c)+f(d)=ac+b+ad+b=ac+ad+2bf(c+d)≠f(c)+f(d)f(c+d)=a(c+d)+b=ac+ad+b\\ f(c)+f(d)=ac+b+ad+b=ac+ad+2b\\ f(c+d)\ne f(c)+f(d)
∴f(x)=ax+b는선형성을만족하지않는다.\therefore f(x)=ax+b는 선형성을 만족하지 않는다.
  • 그렇다면 f(x)=ax+bf(x) = ax + b 를 만족하지 않는 이유는?

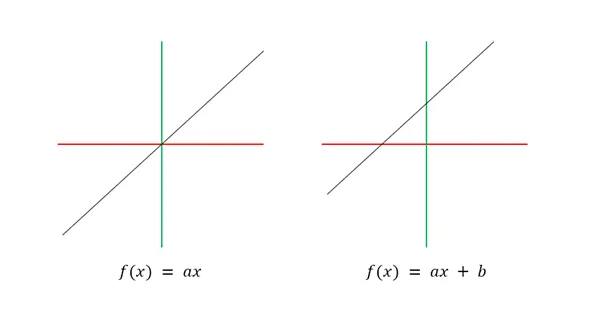
  • 선형성이란 선의 형태를 의미하기보다, 순수하게 인자의 1차 비례 관계로 구성된 대응관계를 의미
  • y=ax+by = ax + b 식에서 b라는 다른 인자가 들어갔기 때문에 순수한 1차 비례 관계가 깨져 선형성을 만족하지 못함

선형성의 해석

가산성(Additivity) : f(x+y)=f(x)+f(y)f(x+y)=f(x)+f(y)
1차 동차성(Homogeneity of 1 degree) : af(x)=f(ax)af(x)=f(ax)

  • 가산성의 성질 : 물과 기름을 섞어서 넣은 결과는 물과 기름을 분리해 넣은 결과와 동일 (다른 불순물이 존재하지 않음)

  • 1차 동차성의 성질 : 어떤 함수는 1차적으로 순수한 비례 관계를 가짐. (불순물이 존재하지 않고 2차 이상의 비례 관계를 가지지 않음.)

선형 사상 (Linear Mapping)

  • 사상과 함수의 차이

    • 함수 (Function) : 집합과 집합의 대응 관계
    • 사상(Mapping) : 집합이 가지는 수학적 체계(공리)를 보존하면서 서로 대응하는 관계

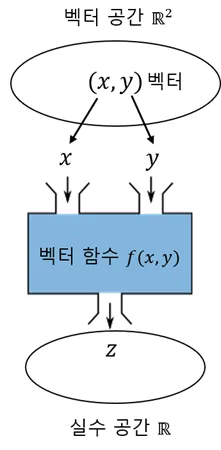
  • 입력의 수와 출력의 수에는 제약이 없음. ( R2→R3\R^2→\R^3 )
  • 벡터 공간이 벡터 공간으로 대응된다는 것은 벡터의 공리를 그대로 유지함을 의미
  • 따라서 이는 넓은 관점에서 사상이라 할 수 있음

사상의 예

f:R2↦R2f((x,y))=(x+y,x⋅y)f:\R^2 \mapsto \R^2 \\ f((x,y))=(x+y, x\cdot y)\\
f:R2↦R3f((x,y))=(x2+y2,x⋅y,2x+3y+2)f:\R^2 \mapsto \R^3 \\ f((x,y))=(x^2+y^2, x\cdot y, 2x+3y+2)

선형성을 가진 사상의 조건

  • f((x1+x2,y1+y2))=f((x1,y1))+f((x2,y2))f((x_1+x_2, y_1+y_2))=f((x_1, y_1))+f((x_2, y_2))

  • f(a(x,y))=a⋅f((x,y))f(a(x,y))=a\cdot f((x,y))

  • 이를 만족하기 위해서는 불순물이 없는 순수한 1차적 대응 관계를 가져야 함.

    • 예제 함수 1) $f((x, y)) = (x + 1, y)

    • x+1x + 1 에 1 이라는 불순물이 들어가 있기 때문에 선형성을 만족하지 않을 것이다

      • 실제로 (3,6)(4,8)(3, 6)(4, 8)을 대입해보면
f((3,6)+(4,8))=f((3,6))+f((4,8))f((7,14))=(4,6)+(5,8)(8,14)≠(9,14)f((3,6)+(4,8))=f((3,6))+f((4,8))\\ f((7,14))=(4,6)+(5,8)\\ (8,14)\ne (9,14)

  • 선형성을 만족하지 않음

    • 예제함수 2) f((x,y))=(3x+4y,2x+3y)f((x,y))=(3x+4y, 2x+3y)

      • 순수하게 xx와 yy간의 1차적인 대응 관계로만 구성되어 있다.

      • 실제로 (1,2)(3,4)(1,2) (3,4)을 대입해보면

f((1,2)+(3,4))=f((1,2))+f((3,4))f((4,6))=(11,8)+(25,18)(36,26)=(36,26)f((1,2)+(3,4))=f((1,2))+f((3,4))\\ f((4,6))=(11,8)+(25,18)\\ (36, 26)=(36,26)

  • 선형성을 만족함을 알 수 있다.

  • 그렇다면 다음의 형태는 언제나 선형성을 만족하는지 확인

    • 두 벡터를 (x1,y1),(x2,y2)(x_1,y_1) , (x_2,y_2)의 미지수로 지정하고 이들이 선형성을 만족하는지 확인

      • 벡터 공간의 공리에 의해
f((x1,y1)+(x2,y2))=f((x1+x2,y1+y2))=a(x1+x2)+b(y1+y2)+c(x1+x2)+d(y1+y2)f((x1,y1))+f((x2,y2))=(ax1+by1,cx1+dy1)+(ax2+by2,cx2+dy2)∴f((x1+x2,y1+y2))=f((x1,y1))+f((x2,y2))f((x_1,y_1)+(x_2,y_2))=f((x_1+x_2,y_1+y_2)) \\ = a(x_1+x_2)+b(y_1+y_2)+c(x_1+x_2)+d(y_1+y_2) \\ f((x_1,y_1))+f((x_2,y_2)) = (ax_1+by_1,cx_1+dy_1)+(ax_2+by_2,cx_2+dy_2) \\ \therefore f((x_1+x_2,y_1+y_2))=f((x_1,y_1))+f((x_2,y_2))\\
kf((x,y))=k(ax+by,cx+dy)=(kax+kby,kcx+kdy)f(k(x,y))=(akx+bky,ckx+dky)∴k⋅f((x,y))=f(k(x,y))kf((x,y))=k(ax+by, cx+dy)=(kax+kby, kcx+kdy) \\ f(k(x,y))=(akx+bky, ckx+dky) \\ \therefore k\cdot f((x,y))=f(k(x,y))
  • 따라서 사상 f((x,y))=(ax+by,cx+dy)f((x,y))=(ax+by, cx+dy) 는 선형성을 만족

선형 사상과 선형 변환

  • 선형 사상 (Linear Mapping) = 선형성을 가진 두 구조의 대응 관계

  • 선형 변환 (Linear Transformation) = 선형성을 가진 벡터 공간과 벡터 공간의 대응 관계

  • 벡터 공간에서는 선형 사상을 선형 변환(Linear Transformation)이라고도 하며 2차원 벡터 공간의 선형 변환은 다음의 형태를 가진다

f((x,y))=(ax+by,cx+dy)f((x,y))=(ax+by,cx+dy)
profile
Woogie_
상상을 구현하는 개발자
이전 포스트

삼각함수

다음 포스트

행렬

0개의 댓글