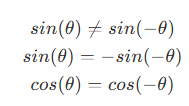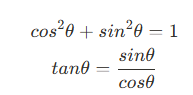삼각함수 (Trigonometric function)
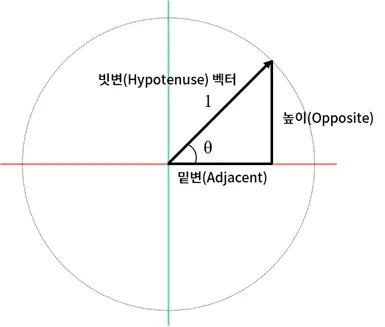
직각삼각형 (Right-Angled Triangle)의 삼요소
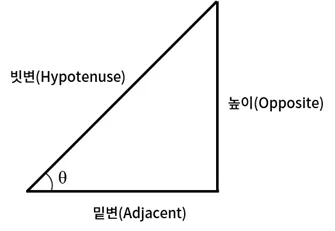
삼각비 (Trigonometric Ratio)
- 직각 삼각형을 구성하는 세 요소 중 두 요소에 대한 비의 값
sin=HypotenuseOpposite
cos=HypotenuseAdjacent
tan=AdjacentOpposite
삼각함수 (Trigonometric Function)
- 삼각비를 집합의 관점에서 대응 관계로 나타낸 것
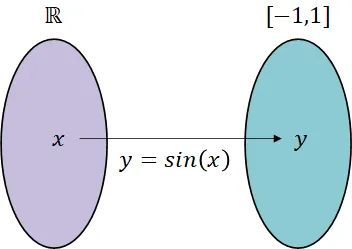
- 정의역 : 실수 집합 R
- 공역 : [-1, 1]
삼각함수와 단위 원
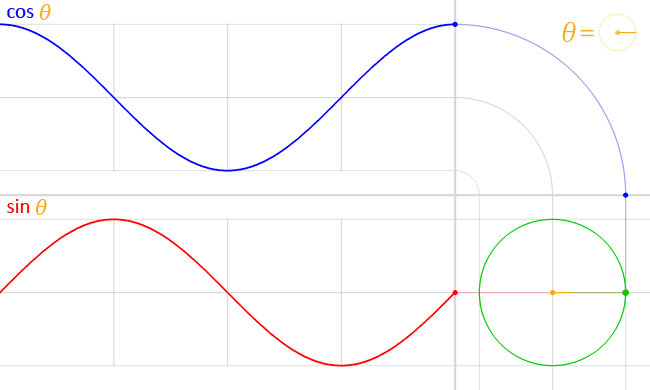
출처 : https://commons.wikimedia.org/wiki/File:Circle_cos_sin.gif
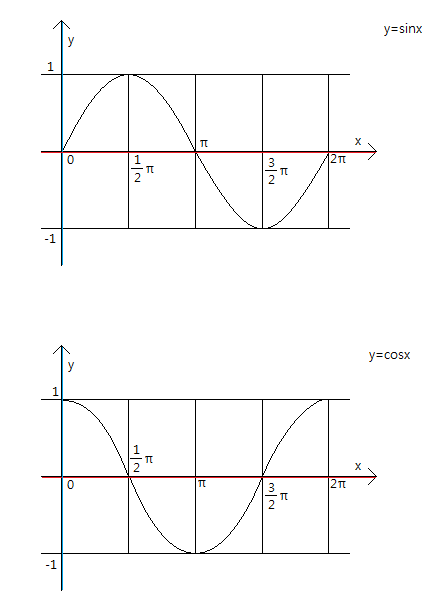
코사인과 사인 함수의 성질
- 사인 함수와 코사인 함수는 항상 [-1, 1] 범위를 일정하게 반복되는 패턴을 갖는다.
- 사인과 코사인 함수는 2π(360°) 단위로 반복된다.
- 축을 기준으로 좌우를 포갰을 때 코사인 함수는 데칼코마니처럼 좌우 대칭인 반면, 사인 함수는 상하가 반전된 형태를 가진다.
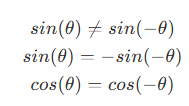
- 탄젠트 함수는 cos90°, cos270°에서 해를 가지지 않는다
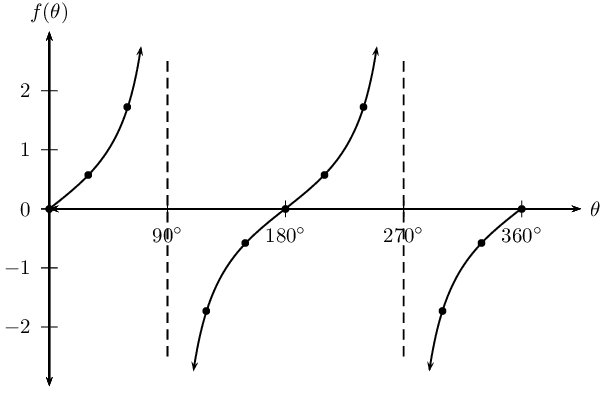
삼각함수의 유용한 공식
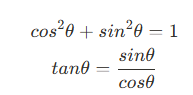
- 원의 반지름 값이 r인 경우, 원호의 좌표는 (cosθ,sinθ) 벡터에 r배 한 결과가 나옴
-
삼각비를 이루기 때문에 위의 공식은 유효
r2cosθ+r2sinθ=r2∴cos2θ+sin2θ=1
-
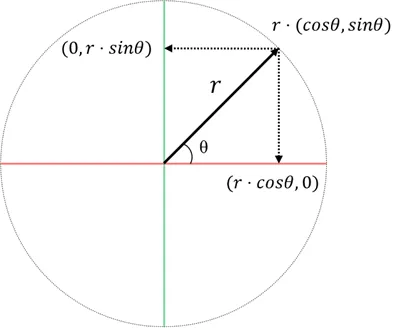
반지름 r인 원호에 위치한 좌표의 분해
r⋅(cosθ,sinθ)=(r⋅cosθ,0)+(0,r⋅sinθ)
-
실벡터공간 R2의 표준 기저 벡터 = 각의 값이 0°와 90°에 해당하는 벡터를 의미
e1=(cos0°,sin0°)=(1,0)e2=(cos90°,sin90°)=(0,1)
각의 측정
각도법(Degree)
- 원을 360개로 균일하게 나누고 °를 사용해 각을 표현
- 왜 360 인가?
- 약수가 많이 나오는 수이기 때문에 원을 쪼개서 계산할 때 유용
호도법 (Radian)
- 하지만 1° 를 단위로 삼아 원래 관련된 수학을 전개했을 때 불편한 점 많음
- 따라서 별도의 단위를 정하고 이를 기준으로 원에 대한 수학을 전개하는 것이 일반적
호도법의 원리
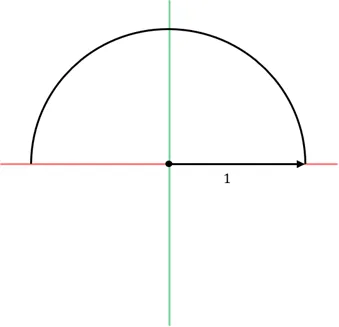
- 원점으로 옮기고
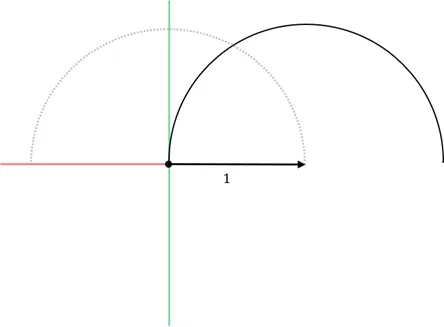
- 원호를 오른쪽으로 펼치면? ⇒ 무리수가 나온다. 이것이 바로 π
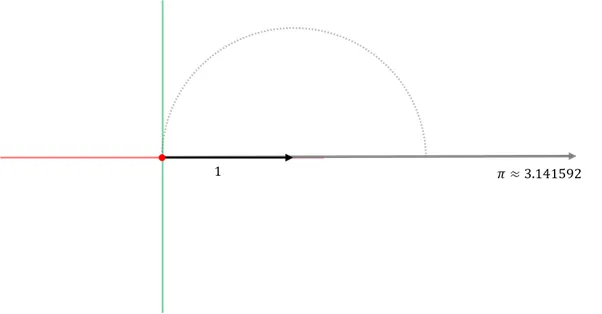
- π중에서 길이가 1인 만큼만 거꾸로 되감는다. ⇒ 이 때 나오는 각 역시 무리수가 됨
- 이것이 호도법의 단위인 래디안(rad)
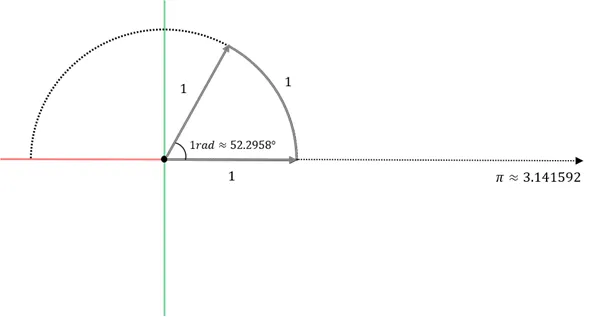
-
π만큼 되감으면 180°에 해당하는 반원이 채워짐
-
이로부터 유도되는 호도법과 각도법의 관계는 다음과 같음
180°=π(rad)1°=180π(rad)1(rad)=π180°
-
자주 사용하는 각도에 대응하는 호도값
90°=2π(rad)60°=3π(rad)45°=4π(rad)120°=32π(rad)
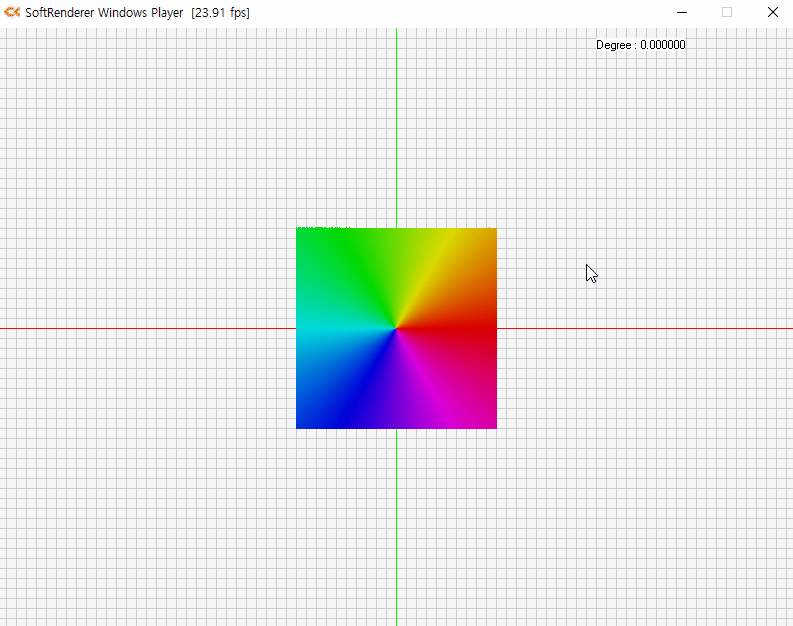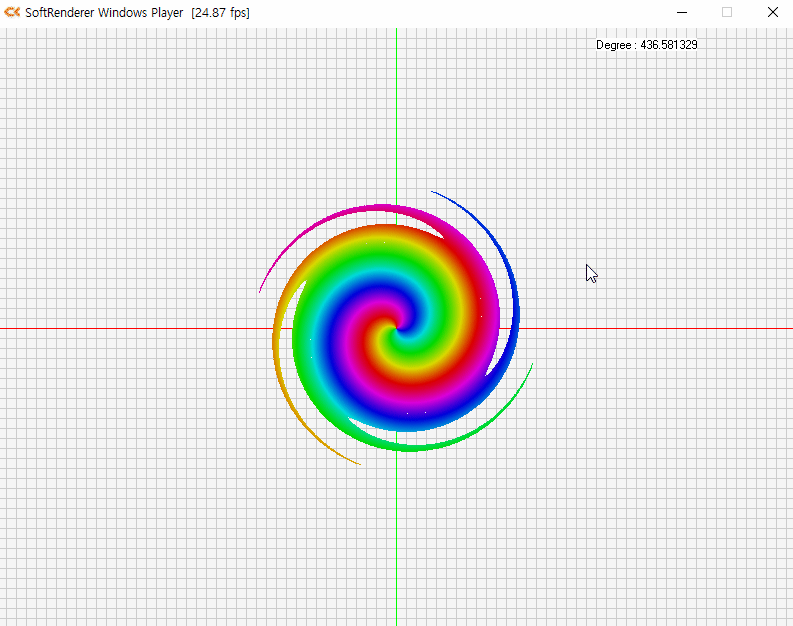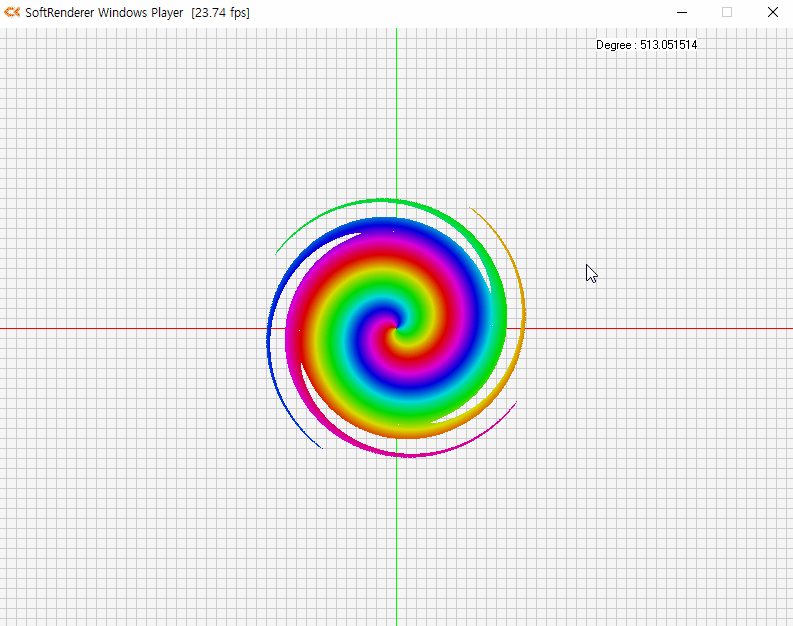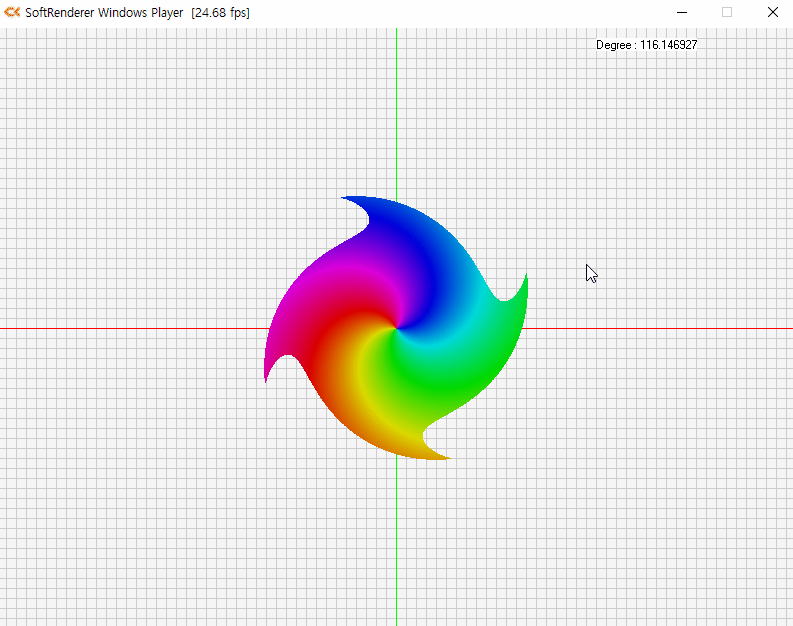
벡터의 회전 (Rotation of Vector)
-
표준 기저벡터를 사용한 실벡터공간 R2의 원소 (x,y)의 생성 방법
(x,y)=x(1,0)+y(0,1)
-
이 때 표준기저벡터로 이루어진 벡터 공간 R2의 두 기저 벡터가 새로운 값으로 변함
-
면 벡터 공간의 원소 (x,y)는 새로운 두 기저 벡터에 각각 x와 y를 곱한 벡터에 대응
-
이 때 새로운 두 기저 벡터가 크기가 1, 직교하는 상태와 현재 방향을 유지하면서 변형하는 것을 회전 변환이라 함.
-
각 θ만큼 발생한 회전 변환을 통해 임의의 벡터 변화 예시
e1↦(cosθ,sinθ)e2↦(−sinθ,cosθ)
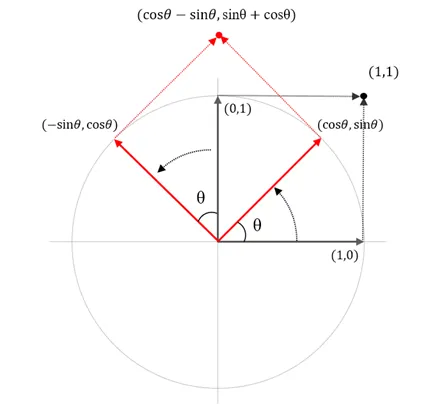
v=(x,y)=x⋅e1+y⋅e2v′=x⋅(cosθ,sinθ)+y⋅(−sinθ,cosθ)=(xcosθ−ysinθ,xsinθ+ycosθ)
삼각함수의 역함수 (Invers trigonometric functions)


-
역함수가 존재하기 위해서는 해당 함수는 전단사 함수여야 함
-
하지만 sin,cos,tan는 전단사함수가 아님. 왜냐하면 단사가 아니기 때문
-
따라서 sin,cos,tan함수를 단사함수로 만들기 위해 의도적으로 정의역의 값을 제한
-
그렇다면 전단사함수가 되어 역함수가 존재 가능
-
사인 함수가 전단사 함수가 될 수 있는 정의역 구간은? : [−2π,2π]
-
코사인 함수가 전단사 함수가 될 수 있는 정의역 구간은? : [0,π]
-
탄젠트 함수가 전단사 함수가 될 수 있는 정의역 구간은? (−2π,2π)
- 참고) [] : inclusive, () : exclusive
-
위의 범위에서 정의한 역함수를 아크사인, 아크코사인, 아크탄젠트 함수라고도 부름
y=sin(x)y=sin−1(x)y=arcsin(x)
삼각함수의 역함수
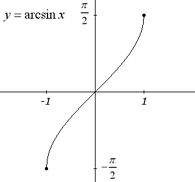
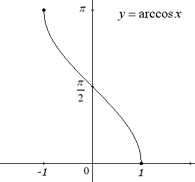
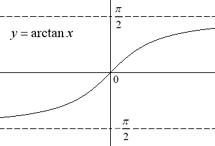
역함수가 다루는 각의 범위
- 아크코사인함수의 치역 : [−2π,2π]
- 아크코사인 함수의 치역 : [0,π]
- 아크탄젠트 함수의 치역 (−2π,2π)
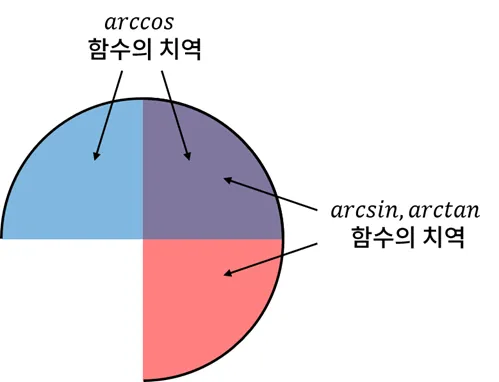
아크탄젠트 함수의 활용
- 두 삼각형은 다른 삼각형이고 다른 각을 가지지만 탄젠트 값은 동일
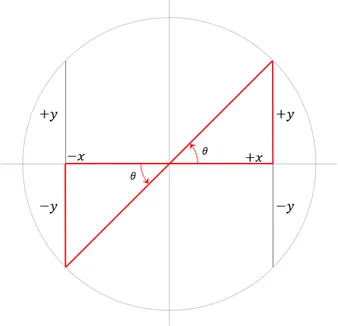
- 하지만 부호정보를 추가로 전달할 수 있다면? -> 둘의 구분이 가능
- 따라서 특별한 탄젠트의 역함수를 사용. 그것이 atan2(y,x) 함수
- 어떤 벡터의 각을 알고 싶다면 탄젠트의 역함수 atan2를 사용
5. 극 좌표계 (Polar Coordinate)
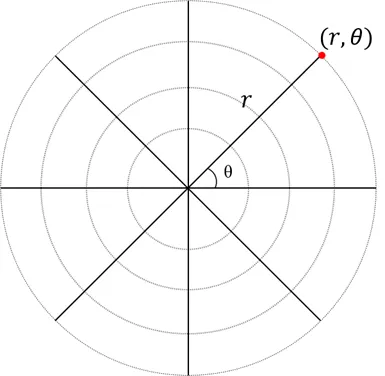
데카르트 좌표계에서 극 좌표계로 변환
$r=x2+y2
θ=atan2(y,x)$
극 좌표계에서 데카르트 좌표계로 변환
x=r⋅cosθy=r⋅sinθ
극 좌표계 활용 예시